The noise immunity of the invariant system of information transmission based on coherent reception under weak correlation communications

The method of analysis of the qualitative parameters of the invariant system using synchronous detector under the weak correlativity of the noise readings is developed. The analytical expression of calculation of the probability density of invariants transition is worked out on the basis of the expression of invariant estimation.

The results obtained under non-correlativity of the noise readings are presented. All this helps to use the offered structure for qualitative transmission of information.

The invariant systems of information transmission can be based on different methods of information processing. The aim is to reduce the influence of the multiplicative noise using the algorithm of the particular information parameter to the training one [1].

The authors considered the four ways of signals processing with the help of invariant relative amplitude modulation and noise readings of different correlativity.

In the paper [1] the invariant relative amplitude modulation (IRAM) under ideal conditions is considered.

In the paper [2] the invariant non-coherent system of information processing is considered.

In the paper [3] the qualitative characteristics of the invariant relative amplitude modulation with the noise in generator are considered.

In the paper [4] the qualitative characteristics of the invariant relative amplitude modulation of the near readings of the information and training signals are obtained. The given paper completes the investigation of the invariant relative amplitude modulation behavior in case of weak correlativity of the readings of information and training signals.

We have a communication channel limited by the frequencies f_l and f_h . The condition of the communication channel is determined by the interval of stationarity inside which the influence of multiplicative noise is described by the channel transmission k ( t ) on a certain frequency.

Multiplicative noise equally corrupts informational and training parts of the block of transmitted signals. However the ratio of the energy of the information signal to the energy of the training signal is constant on the interval of stationarity.

Besides, each transmitting block is influenced by the additive noise.

It is supposed that the nearest readings of the additive noise are weakly correlated with each other.

It is necessary to calculate the probability of the pairwise transition of invariants in the system under consideration. For this purpose the analytical expression of the density of probability of invariant estimation is to be found.

In figure 1 the structure of the receiving part of the invariant relative amplitude modulation is presented. Such structure contains synchronous detector (multiplier, AFCc, LPF) and special calculator.

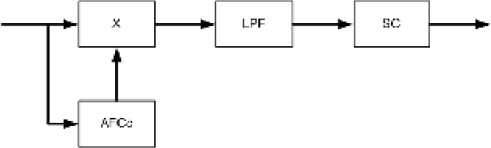
Fig. 1. Block diagram of invariant system of information transmission: AFCc is an automatic – frequency control circuit, LPFisalow – pass filter, SC is a special calculator

On the transmitting side, the modulating parameter is put into the ratio of the energy of the information signal to the energy of the training signal.

Owing to the fact that multiplicative noise equally influences both parts of each transmitted block, the algorithm of demodulation of reception signals taking into consideration the chosen method of signals processing will consist in the expression of invariant estimation:

∑ ^N ( k ⋅INV l + ( i ))

INV L ^* =      _N ^{i = 1} _L                         ⋅ S tr .            (1)

¹ _L ∑∑ ( k ⋅ S tr +11( m , j ))

L j = 1 m = 1

In the numerator (1) the N sum of instantaneous readings of the signal of the information impulse is presented. The information signal is formed by the rectangular envelope with the amplitude k ⋅INV _l +( i ),where ξ ( i ) is additive noise readings distributed according to the normal law [5].

In the denominator (1) the sum N of instantaneous readings of the signal of the training impulse formed by the rectangular envelope is represented: k ⋅ S _tr + η( m , j ), where η( m , j ) is the noise the m-realization of the training signal, distributed according to the normal law [5].

Without loss of generality we suppose that S _tr = 1. If S _tr ≠ 1, then all outcome parameters, namely INV _l and σ_ξ (root-meansquare deviation of the noise ξ( i ), η( m , j )) can be scaled by the quality S _tr. In this case the formula (1) will be changed due to the introduced restrictions as follows:

N

∑ ( k ⋅INV l +( i ))

INV ^* = ^{i = 1}

L   NL

¹ _L ∑∑ ( k ⋅ S tr +n ( m , j )) L j = 1 m = 1

A _.

B

Intheformula(2) k ⋅INV _l istheinstantaneousreadingof the signal of the information part of the impulse, coming from the channel; ξ( i ) – i – is instantaneous value of the noise in the information signal; k is coefficient of transmission of the channel; η( m , j) – j – is instantaneous value of the noise in m-realization of the training signal.

Let us suppose that the occasional values ξ( i ) and η( m , j ) are equally distributed according to the normal law with the zero mathematic expectation and the dispersion σ_ξ². Besides, it is supposed that in each block only the next occasional values are dependent. Then

CORR (ξ( i ), ξ( i –1)) =CORR (η( m , j ), η( m , j – 1)) = R , where R is coefficient of correlation.

All the other occasional values entering each receiving block will be independent. For the realization of this model it is necessary that [6]

| R |≤1/V2^.

Let us use the known way of estimation of the probability of the pairwise transition described by the formula of the full probability.

Zp                ∞

P _tr = P ₁ ∫ w_i ( z ) dz + P_i ∫ w ₁( z ) dz ,            (3)

0Zp where Ptr is the probability of transition of INVl into INVi and vice versa; P1 is the probability of appearing of INV1. Pi is the probability of appearing of INVi, where INV1 is sent. The second integral the probability of appearing of INV1 when INVi is sent; Zthr is threshold value, necessary for calculating Ptr; when P1 and Pi are known it is calculated with the help of the best bias estimation by minimization of Ptr on Zthr. When P1 and Pi are unknown we choose P1 =Pi = 0.5.

From the analysis (3) we can see that for calculation of P _tr it is necessary to know the analytical expression W ₁( z ) and W_i ( z ) of the probability density of the estimation of the invariant. On the basis of (2) let us calculate the mathematic expectation and dispersions of the instantaneous values A and B .

Mathematic expectation of the numerator is equal to [7]

mA = N⋅k⋅INVl.

But mathematic expectation of the denominator is equal to[7]

mB = N■ k.(5)

The dispersion of the numerator is [7]

GA = D (£ ^i)) = N ■ g? + 2( N - 1)co<( i), ^( i +1)) = i =1

= N ■ c2 + 2( N -1) R■g? = o2( N + 2( N -1) R).(6)

The dispersion of the denominator is equal to [7]

о B = lo*(N + 2( N -1) R).(7)

The quotient of the two occasional values is calculated by the formula [7]

rn                - ⁽ zx ^- mA ⁾²     - ⁽ x ^- mB ⁾²

W (z) =f----1----e 2aA ■ e 2oB IxIdX,(8)

-„ 2!A4BB where сл and aB are calculated by the expressions (6) and (7); mA mB – by the expression (4, 5).

It should be pointed out that in the process of calculation in the formula (3) W_i ( z ) – INV _i , is used where i =2,3,4,5,6,7. The value of the probability of the pairwise transition P _tr was calculated using the method of numerical integration. The number of accumulations with averaging is 40 [1].

The received data are limited by the first 6 pairs of the compared invariants, when INV₁ =1,INV _i =2,3,4,5,6,7.

The probability of the pairwise transition is calculated at the value h – signal/noise relations which was calculated by the formula expressed by the relation of the power of signal to the power of noise [5]

h - = k 2^ NV 2

N ²

.

The threshold values Z _thr were calculated by minimization P _tr in the formula (3). The results of the calculation for different values of the coefficient of the channel transmission k , the coefficient of correlation R and the quantity INV _l =1, INV _i =2, 3, 4, 5, 6, 7areplacedintables1, 2.

If in the formulas (6) and (7) R = 0 (the readings of the noise are non-correlated) the general expression of probability density of the invariant estimation obtained in the paper turns into the relation of the calculation of the analogous parameter received under the operation of the non-correlated readings of the white noise [1].

However, the received expression of the density of the probability in the given paper is redetermining and most fully reflects the real situation.

The peculiarity of any invariant system based on the principle of the invariant relative amplitude modulation is the fact that the amplitude modulated signals formed by INV _l and S _tr are transmitted along the channel.

The transmission of these signals is carried out on the basis of classical algorithms of information processing and has no high noise immunity.

The curve 3 in figure 2 and figure 3 corresponds to the error probability P _er, which is the analogue of the probability of the pairwise transition P _tr and is calculated by the known formulas (5) and only after processing of these signals in accordance with the algorithm of the quotient by the expression (1), we obtain the invariant estimation which is in reality a number but not a signal. As we can see from figures 2 and 3, the probability of the pairwise transition in the invariant system is defined by the quantities (10^–1...10^–33). At the same values the signal/noise probability of the inaccurate reception of the single symbol in classical systems is within the limits (10^–1...10^–7).

The given analysis of the invariant system shows that the invariant system of information transmission under the weak correlation of the readings of the additive noise has a high noise immunity. The error probability of the classical algorithm with the amplitude modulation is at least twice as large as the probability of the pairwise transition in invariant system.

Therefore, the given system should be used in telecommunication systems, telecontrol systems and other systems, placing exacting demands upon the noise immunity.

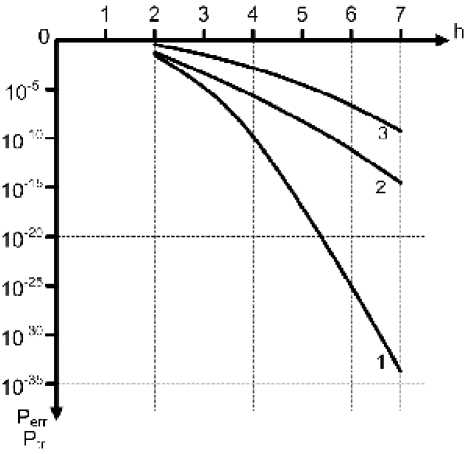
Fig. 2. The noise immunity of IRAM at k = 1 andINV _l =1;INV _i =2;3;4;5;6;7.

Curve 1 is the probability of the pairwise transition into IRAM under non-correlativity of the noise readings (theoretical limit); Curve 2 is the probability of the pairwise transition of IRAM at R = 0,7; Curve 3 is the error probability of the classical

The value Z _thr at the given K , R

Table 1

K = 1				R = 0.7
Z thr	1.627	2.057	2.488	3.062	3.516	4.162

Table 2

The value Z _thr at the given K , R

K = 0.7				R =0.7
Z thr	1.820	2.226	2.632	3.038	3.646	4.078

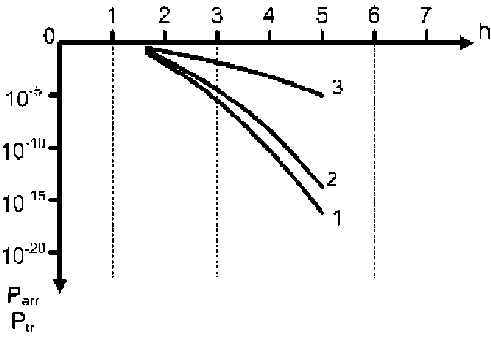
Fig. 3. The noise immunity of IRAM at k =0,7 andINV _l =1;INV _i =2;3;4;5;6;7.

Curve 1is the probability of the pairwise transition into IRAM under non-correlativity of the noise readings (theoretical limit;

Curve 2 is the probability of the pairwise transition of IRAM at R = 0,7; Curve 3 is the error probability of the classical