The Platform Built Based on the Mode operations of AES and the Image Applications
Автор: Chi-Wu Huang, Ying-Hao TU, Shih-Hao Liu, Hsing-Chang Yeh
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 4 vol.3, 2011 года.
Бесплатный доступ
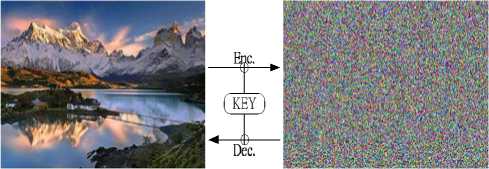
This paper presents an image encryption instead of text to observe the block cipher modes of operation of the complex AES processing. A platform is built based on the mode operations for the experiments. The cipher image of ECB may appear patterns due to the identical color inputs. CTR and MCTR make those identical inputs different by adding counters to remove the patterns while CBC, CBF, and OBF do it by adding serious Cipher function outputs which are almost random numbers. The mode features resulted from adding number series and the ways of addition, are discussed and compared, which help to design the Switching Control to configure all the modes into a platform for the AES mode operations and image test.
AES, Image Processing, Entropy, ECB , CTR.
Короткий адрес: https://sciup.org/15010103
IDR: 15010103
Текст научной статьи The Platform Built Based on the Mode operations of AES and the Image Applications
Published Online July 2011 in MECS
The Advance Encryption Standard (AES) was announced by the Nation Institute of Standard and Technology (NIST) in 2001.[1,2] It is a symmetric block cipher that is intended to replace DES as the approved standard for a wide range of applications, such as highspeed web-server[3,4], wireless communication[5,6], low-power smart card and RFID.[7,8] In the same year, the cipher block modes of operation were also published to fit AES more easily for such a wide range of applications.[9]
Basically, AES includes three main processes, KeyExpansion (key expansion), Encryption, and Decryption. The 128-bit plaintext and key are added (xored) to be encrypted to become a ciphertext which looks just like a random number and hides the plaintext. However, by using the same key, the ciphertext can be decrypted back to plaintext as shown in Figure 1.
Plaintext
I 00112233445566778899aabbccddeeff I
600 600 600
700 700
600 600 500 500 500
500 500 400 400 400
300 300 300 300 300
Red Entro Green7.6543 Blue
Red Entrop Green7.9991 Blue
B 200 200 200 200200
100 100 100 100100
100 200 0 100 200 0 100 200
0 100 200 0 100 200 0 100 200
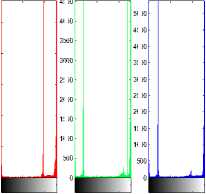
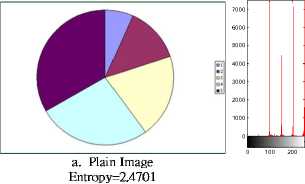
Figure 2. The plain image and ECB cipher image.
| Decryption |
V Key
( ООО 102030405060708090aObOcOdOeOf)
| Encryption |
1 r Ciphertext
I 69c4e0d86a7b0430d8cdb78070b4c55a
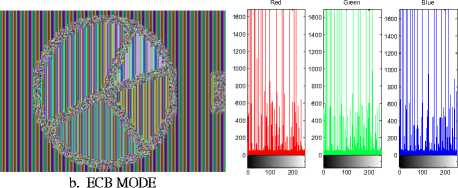
However, sometimes a pattern is appeared in cipher image if plain image has an identical color at the related area, or the shape of a picture is not hided if it contains many identical colors as shown in Figure 3. Those cipher images having patterns apparently are not random enough.
In case of text message encryption, the same random number repeated if the plaintext is identical in encryption as shown in Fig. 4. Yet, the repeated ciphertext is rather uneasy to be found if it is not displayed with the multiple of 128-bit widths. Besides, identical texts in a message are always the rare case.

Red Green Blue

0 100 200 0 100 200 0 100 200
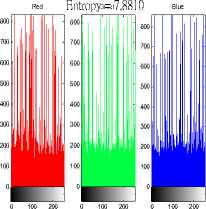
Figure 4. The ciphertext repeated at the area of plaintext ’1’.

Entropy=4.2571

histogram of Red histogram of Green histogram of Blue
histogram of Red histogram of Green histogram of Blue
0 100 200 0 100 200 0 100 200
(a) Plain image.

0 100 200 0 100 200 0 100 200
(b) Cipher image.
Figure 3. Patterns and Shape appear in ECB cipher image.
From the above observation, we know it is the identical colors that cause patterns appearing or the shape not being hided. This is a drawback of AES operation. A straight forward idea to overcome the drawback may be just make those identical color inputs different by adding different number series.
This paper presents the observation of all modes based on the “adding number series and the ways of addition” to obtain the features of each mode at the later sections. A platform, based on the three units of KeyExpansion, Encryption, and Decryption, is built for all cipher modes of operation .
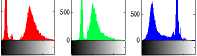
For giving the feeling and measuring the degree of noise randomness in image, RGB histograms and Entropy (1) are presented. The 256 grey levels are represented at the x-axis, and the numbers of those RGB grey levels appeared are dispalyed at the y-axis of the historrams. One can finds, from Fig. 2 and Fig. 3, that a pictures with more uniformly distribued RGB histograms has antropy value closer to 8.
The Entropy is defined as follows [11,12];
n 1 n
Entropy = Z P ( a , )log p, ' : - Z P ( a, )log P ( a j )
1"1 7 P ( a ,j ) 1:1
An image pixel is the grey level combinations of RGB. In this application, one byte is used to represent a color which has 256 (n=28=256) grey levels and the calculated values of entropy are between 0 and 8, for examples:
-
• A Black image having RGB values of (0, 0, 0), the probability for 0 is 1, and entropy = 1*log 2 1 = 0. A white image (255, 255, 255) also has entropy = 0.
-
• An image, with four equal areas of red (255,0,0), green (0,255,0), blue (0,0,255) and gray (98,98,98), has the probabilities 1/4, for 98 or 255, and 1/2 for 0. Entropy= 2*1/4*log 2 4 + 1/2*log 2 2 = 1.5 .
-
• A full color image with the grey levels 0 through 255 appeared in the uniformed distribution, the probability for each grey level is 1/256, and the entropy = 256*(1/256*log 2 256) = 8 .
The rest of this paper is organized as follow; brief AES algorithm and ECB mode are described in Section II; block cipher modes of operation are described in Section III; experiments and a platform for modes of operation is described in Section IV; and some conclusions are made in Section V.
-
II. A ES A LGORITHM AND ECB MODE
-
A. Algorithm
The AES algorithm is a round-based symmetric block cipher that processes data block of 128 bits using a cipher key of 128, 192, or 256 bits. A sequence of four primitive functions, SubByte, ShifRow, MixColumn and AddRoundKey, form a loop called a round, to be executed Nr-1 time. The number of iteration loop Nr can be 10, 12, or 14 depending on the size of key. SubByte operation is a nonlinear byte substitution that operates independently on each byte of the state using a substitution table. ShiftRow operation is a circular shifting on the rows of the state with different numbers of bytes (offsets). MixColumn operation mixes the bytes in each column by the multiplication of the state with a fixed polynomial (3x3+x2+x+2 for encryption, bx3+dx2+9x+e for decryption) modulo x4+1. AddRoundKey operation is an XOR process that adds a round key to the state at each iteration loop. [1,19]
Figure 4 summarizes the AES algorithm in two flow diagrams, MixColumn is not performed at the last round, the sequence of SubByte and ShiftRow can be switched without affecting the final cipher output.
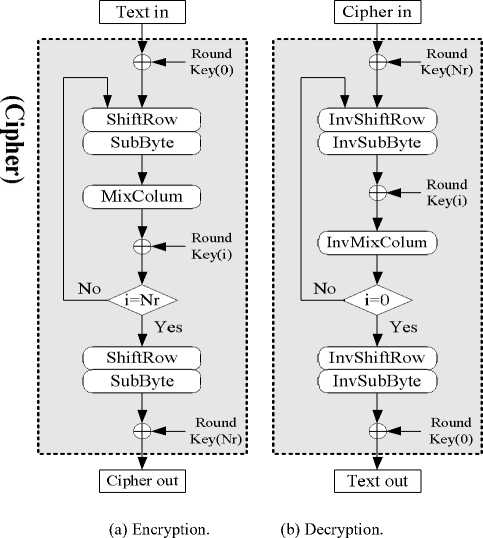
Figure 5. AES encryption / decryption.
(Decipher)
-
B. KeyExpansion
Figure 6 shows the four 32-bit words W 0 ,W 1 ,W 2 ,W 3 to constitute 128-bit key for the expansion process, where K 0 ,K 1 ,K 2 ,K 3 are the cipher key inputs to be expanded to 10 around keys. During the expansion, W 3 always goes through RotWord(RW), SubWord(SW) and AddRcon(AR), and XorWord(XW) in series for each round, which are defined as follows;
-
• RotWord : Take a 4-byte word input and perform a cyclic permutation.
-
• SubWord : Take a 4-byte input word and apply as S-box to each if the 4-bytes to produce an output word.
-
• AddRcon : Add (XOR) Rcon to the most significant byte of a 4-byte word where Rcon has one value for each round, all the 10 values are 01,02,04,08,10, 20,40,80,1b,36.
-
• XorWord : Add (XOR) w 0 , w 1 , w 2 , w 3 in series to obtain one of the 10 round keys as shown in Figure 6.
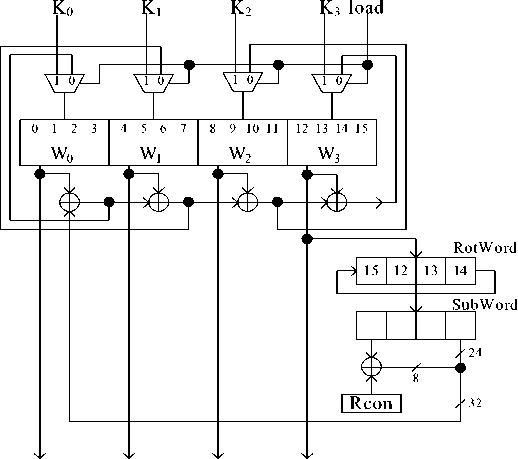
W 0 W 1 W 2 W 3
Figure 6. KeyExpansion block diagram .
-
C. ECB mode
Two gray-dotted blocks, one at Encryption in Figure 5-a while the other at Decryption in Figure 5-b, are defined as Cipher function CIPH k ( ) and Decipher function DECI k ( ) , respectively. Figure 4 then can be simplified by using Cipher as well as Decipher shown in Figure 7, and it is exactly the block diagram of ECB mode representation described by the NIST publications.[13] So far encryption uses Cipher and decryption uses Decipher in ECB. Yet, sometimes decryption may also use Ciphers instead of Deciphers in some other modes described in next section.
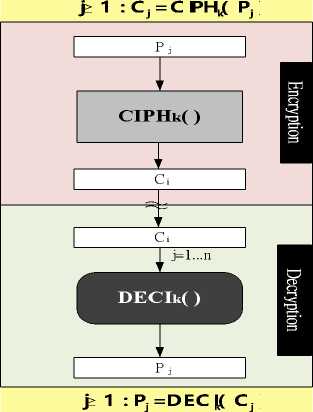
Figure 7. ECB mode.
-
III. B LOCK C IPHER M ODES OF O PERATION
As mentioned before, adding different numbers to the identical plaintext (Pj) is one way to overcome the drawback of ECB mode, then the Initial Count (IC) initiated counter sequences (Tj) is a convenient choice.
-
A. Modified Counter modes
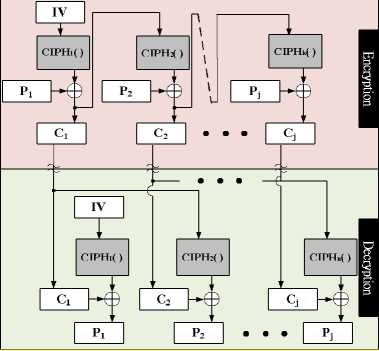
Fig. 8 Shows the Tj modified ECB, where Pj is modified by Tj at the input of CIPH k ( ) in encryption while Cj is modified by Tj at the output of DECI k ( ) in decryption.
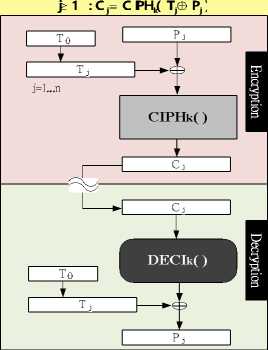
> 1 : P j = T j ® DEC( C j
Figure 8. MCT mode
-
B. Counter modes
We call Fig. 8 the Modified counter (MCT) mode, because Counter (CTR) mode, defined in the NIST publications, also uses Tj for modification. Yet, the modification occurs only at the output of CIPH k ( ) in both encryption and decryption, as shown in Fig. 9. Both CTR and MCT can remove the pattern from Cipher image. CTR is a smart design in terms of hardware implementation, because only CIPH k ( ) is used, saving more hardware resources than MCT which requires both. [15,16,18]
j' 1 :C , = Р , ® CPH(T j )
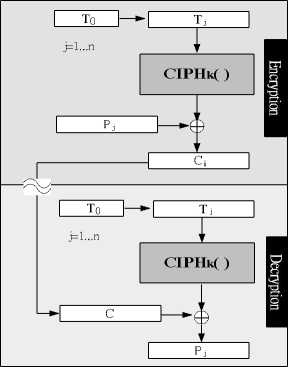
к 1 : P , = C , ® CPH(T j )
Figure 9. CTR mode.
By careful observation from Fig.8 and Fig.9 It is interesting that two rules can be found and that they hold true for the three modes to be described later. Two rules are in the following.
-
• Ciph-in-deci-out: If Pj is modified at the input of CIPH k ( ), then Cj is modified at the output of DECI k ( ).
-
• Cipher-out-both: If only CIPH k ( ) is used in encryption/decryption, then both are modified at the output.
Three other modes defined in NIST publications are Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB). [17] They use Initial Vector (IV) initiated random numbers instead of count series in CTR and MCT. The numbers are random because they are generated through CIPH k ( ) function in series.
-
C. Cipher Block Chaining modes
Fig.10 shows the Cipher Block Chaining mode. Ciph-in-deci-out rule holds true for it and the random numbers replace count series. Fig.10 is expressed in parallel flow diagram, yet parallel operations do not gain speedup over serious operations in encryption, because IV has to ripple through all the n blocks to reach the final Cj(j=n). However, Parallel operations do gain speedup in decryption as long as Cj(J=1…n) is available at beginning. Errors in Pj encryption may propagate to the end block since they are involved in the serious cipher functions while errors in Cj decryption only propagate to the next block.
j=1 : C j = CPH( V ® P)
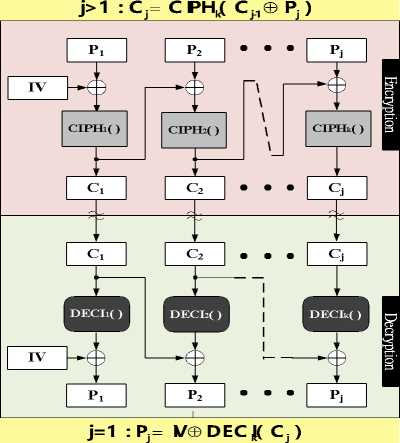
j>1 : P j = C j ® DEC ( C -1 )
Figure 10. CBC mode.
-
D. Cipher Feedback modes
Fig. 11 shows the CFB mode where the rule of Cipher-out-both holds true for it. The random numbers involved Pj modification has no speedup gain in parallel encryption while it does have speedup gain in parallel decryption. Error propagation in Pj and Cj, are all the same as CBC.
= 1 : C j = P j ® CPH( V)
>1 : C j = P® CPH(CH )
j=1 :P j = C j ® DEC( V )
>1 :P j = Ся® DEC( C j )
Figure 11. CFB mode.
-
E. Output Feedback modes
Fig. 12 shows the OFB mode where the rule of Cipher-out-both still holds true for it. However, the parallel operations are suitable because the random numbers involved can be pre-calculated and stored for the later OFB processing in both encryption and decryption. No error propagation involved in OFB encryption/decryption.
= 1 : O j = C PH( V ) Cj = P j ® Oj
>1 :Oj = CPH(OH ) Cj = P j ® Oj
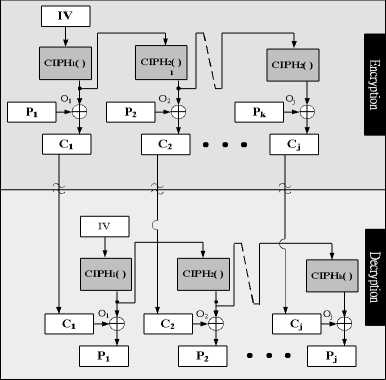
j=1 :O j = CPH( V ) P j = C j ® O j
>1 :O j = CPH(OH ) P j = C j ® O j
Figure 12. OFB mode.
-
F. Modes Comparison
Comparisons based on the number series selected for plaintext modifications, the ways they are modified, and the parallel operations as well error propagation, are list in the following;
-
1) Number series used:
-
• CTR, MCTR use counter sequences and are block independent.
-
• CBC, CFB, and OFB use random numbers with block dependent processing.
-
2) The way of modification:
-
• The rule of Ciph-in-Deci-out is applicable to the input modification of MCT and CTR
-
• The rule of Ciph-out-Both is applicable to the output modification of CBC, CFB, and OFB.
-
3) Parallel operations/error propagations:
-
• ECB, CTR, and MCTR can perform Encryption or Decryption in parallel due to their block independence.
-
• CBC, CFB, and OFB cannot perform Encryption in parallel due to the serious Cipher functions involved except OFB, in which the serious Ciphers can be pre-computed and stored for being used in later parallel operations.
-
• The parallel operations of Decryption in all modes can be performed since all ciphertexts are available at the beginning of Decryption process.
-
• No error propagation of Pj and Cj in ECB, CTR, MCT, also no error propagation of Cj in OFB. Errors of Pj in CBC and CFB are propagated to the end block while errors of Cj in OFB is propagated to the next block only.
The plain images of Target-shaped picture and a Pieshaped picture are used for the experiments of six-mode encryption/decryption operations, both shown in Fig. 14 and Fig.15. It is clear that ECB is not hiding from cipher image and all other modes are hiding it quite well.
However, by careful observation, It is interesting to find that there is a small difference between the count series modified encryptions of MCT, CTR and the random numbers modified encryption of CBC, CFB, and OFB. We can see the histograms of CTR and MCT are not so much uniformly distributed as those of CBC, CFB, and OFB in Fig.15-c as well as Fig. 15-d, and very implicit patterns can be seen in the cipher images of CTR and MCT. But there is no different in using Targetshaped image encryptions in Fig.14-c and Fig. 14-d from the other modes of CBC, CFB, and OFB. The difference between the coun-series modified encryption and the random-number modified encryption might be an issue for further investigation.
TABLE I.
S IX MODES OF AES OPERATIONS
|
Mode |
Number Series added |
Parall operations |
Error propagation |
Encryption Pattern generated |
|
ECB |
NO |
OK |
NO |
Sometimes |
|
MCT |
Count sequences |
OK |
NO |
NO or very implicit |
|
CTR |
Count sequences |
OK |
NO |
NO or very implicit |
|
CBC |
Random numbers |
EncryptionNO |
To the end block |
NO |
|
Decryption: OK |
To the next block only |
|||
|
CFB |
Random numbers |
Encrypti on :N 0 |
Tо the end block |
NO |
|
Decryption: OK |
Tо the next block only |
|||
|
OFB |
Random numbers |
OK if pre-caculated |
NO |
NO |
Table 1 shows the summaries of the experiments and some features based on each modes operation .
IV. P LATFORM C ONFIGURTION AND E XPERIMENTS
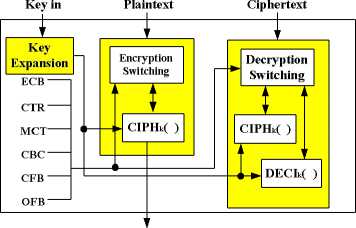
The switching control, based on the analysis in the previous section, combines KeyExpansion, Encryption, and Decryption to construct a platform for the mode operations in shown in Fig.13.
Red Green

100 200

0 100 200
x 104 Blue

0 100 200
Ciphertext
Figure 13 The block diagram of six-mode platform for AES
a. Plain Image Entropy=4.2157

Red Green Blue
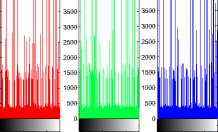
0 100 200 0 100 200 0 100 200
Green
Blue

Red
Green
Blue
1000 1000
500 500
0 100 200
0 100 200
0 100 200
c. MCI MODE Entropy=7.9998

Green Blue
1000 1000
500 500
0 100 200 0 100 200 0 100 200
d. CTR MODE Entropy=7.9994

Green Blue
1000 1000
500 500
0 100 200 0 100 200 0 100 200
e. CBCMODE Entropy=7.9998

Red
Green
Blue
1000 1000
500 500
0 100 200
0 100 200
0 100 200
f. CEB MODE Entropy=7.9998

Red
Green
Blue
1000 1000
500 500
0 100 200 0 100 200 0 100 200
g. OFBMODE Entropy=7.9998
Figure 13. Encryption experiments of the six modes using Targetshaped picture.
Red
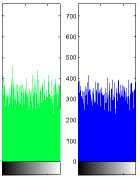
Entropy=6.6185

c. MOT MODE
Entropy=7.9R43

d. .CTR MODE Entropy=7.9844

e. CBCMODE Entropy=7.9794

f. CEB MODE Entropy=7.9991
0 00 JI
0 100 200
Red

0 100 200
Red
Green Blue
0 100 200
0 100 200
Green
Blue
0 100 200 0 100 200
Green
Blue
0 100 200 0 100 200 0 100 200
Red
Green
Blue
0 100 200 0 100 200 0 100 200
Red
Green

g. OFB MODE Entropy=7.9992
Blue
0 100 200 0 100 200 0 100200
Figure 14. Encryption experiments of the six modes using Pie-shaped picture.
-
V. C ONCLUSIONS
This paper presents the image encryption to observe the block cipher modes of operation to help understand the complex AES processing. The cipher image of ECB may appear patterns due to the identical color inputs. Making those identical inputs different by adding number series to remove the patterns is proposed and tested.
The image compression before encryption is the other way to overcome the ECB drawback, because the same colors are always to be removed during compression. Then, ECB becomes one of the best choices due to its simple as well as easy implementation.
The small differences between the count-series modified MCT, CTR image encryption and the randomnumber modified CBC, CFB, and OFB encryption might be an issue in future investigation
Список литературы The Platform Built Based on the Mode operations of AES and the Image Applications
- NIST Announcing the Advanced Encryption Standard (AES), FIPS 197. Technical report, National Institute of Standards and Technology, November 2001.
- NIST: National Institute of Standards and Technology http://wwwnist.gov/
- Xinmiao Zhang, Keshab K. Parhi, “High-Speed VLSI Architecture for the AES Algorithm.” IEEE Transaction on VLSI System, vol 12, No. 9, September 2004.
- A. Hodjat, “Area-Througput Trade-Offs for Fully Piplined 30 to 70 Gbits/s AES processors,” IEEE TRANSACTION on COMPUTERS, vol. 55, no. 4, pp 366-372, April 2006.
- Sivakumar, C.; Velmurugan, A., High Speed VLSI Design CCMP AES Cipher for WLAN(IEEE 802.11i)2007, Signal Processing, Communications and Networking, 2007. ICSCN '07, International Conference on.
- Samiah, A., Aziz, A., Ikram, N., “An Efficient Software Implementation of AES-CCM for IEEE 802.11i Wireless St,” International Confronce on COMPSAC 2007, pp. 689 – 694.
- Schramm K.; Paar C. “IT security project: implementation of the Advanced Encryption Standard (AES) on a smart card.” Information Technology: Coding and Computing, 2004. Proceedings, ITCC 2000 International Conference on.
- Man, A.S.W., Zhang, E.S.; Lau, V.K.N.; Tsui, C.Y. Luong, H.C., “Low Power VLSI Design for a RFID Passive Tag Baseband System Enhanced with an AES Cryptography Engine.” RFID Eurasia, 2007 1st Annual.
- Morris Dworkin, “Recommendation for Block Cipher Modes of Operation” NIST Special Publication 800-38A 2001 Edition.
- Kuo-Huang Chang, Yi-Cheng Chen, Chung-Cheng Hsieh, Chi-Wu Huang, Chi-Jeng Chang, “Embedded a Low Area 32-bit AES for Image Encryption/Decryption Application” IEEE ISCAS 2009, pp 1922 – 1925, May 2009.
- Rafael C. Gonzalez and Richard E. Woods, Steven L.Eddins, Digital Image Processing using MATLAB, Prentice Hall, 2004.
- Rafael C. Gonzalez and Richard E. Woods, Digital Image Processing, 2/E, Prentice Hall, 2001.
- P. Rogaway, M. Bellare, and J. Black. OCB: A block-cipher mode of operation for efficient authenticated encryption. ACM Transaction on InformationSystems Security, 6(3):365–403, 2003.
- G. Bertoni, L. Breveglieri, P. Fragneto, M. Macchetti, and S. Marchesin. Efficient software implementation of AES on 32-bits platforms. In Proceedingsof the CHES 2002, LNCS vol. 2523 pp. 159–171. Springer, 2002.
- Y. Fu, L. Hao, and X. Zhang. Design of an extremely high performance counter mode AES reconfigurable processor. In Proceedings of the Second International Conference on Embedded Software and Systems (ICESS’05),pp. 262–268. IEEE Computer Society, 2005.
- H. Lipmaa, P. Rogaway, and D. Wagner. Comments to NIST concerning AES Modes of Operations: CTR-mode encryption, September 2000, available at the website of http://www.cs.ucdavis.edu/rogaway/papers/ctr.pdf.
- D. Chakraborty and P. Sarkar. A general construction of tweakable blockciphers and different modes of operations. In H. Lipmaa, M. Yung, and D. Lin,editors, Inscrypt, LNCS, vol. 4318 pp. 88–102. Springer, 2006
- F. Charot, E. Yahya, and C. Wagner. Efficient modular-pipelined AES implementationin counter mode on ALTERA FPGA. In P. Y. K. Cheung,G. A. Constantinides, and J. T. de Sousa, editors, FPL, LNCS, vol. 2778,pp. 282–291, Springer, 2003.
- A. Rudra, P. K. Dubey, C. S. Julta, V. Kumar, J. R. Rao, and P. Rohatgi. Efficient Rijndael encryption implementation with composite field arithmetic.In Proceedings of the CHES 2001, LNCS, vol. 2162, pp. 171–184. Springer,2001


