The Research of Unconditionally Secure Authentication Code For Multi-Source Network Coding

Published Online March 2011 in MECS

In a traditional communication network, the messages are transmitted from the source to the destination via intermediate nodes. Network coding was first proposed by Ahlswede et al. [1] in order to maximize the throughput of multicast networks, intermediate nodes not only can store and forward the messages, but also can encode the received messages before forwarding them. Li et al. [2] showed that linear coding suffices to achieve the maxflow from the source to each receiving node in multicast network, where intermediate nodes generate outing messages as linear combinations of their incoming messages. With the application of the network coding, the usage of network resources was improved. So the network coding was widely used.

However, as network coding allows intermediate nodes to encode the received messages, the result is that network coding is very vulnerable to pollution attacks. Pollution attacks, which consist of injecting malicious messages in the network. The malicious messages may come from the modification of received messages by a malicious inter-mediate node or from the creation of bogus messages by an outside adversary. As a result, with using network coding, the detection for integrity and origin of the messages received is very important. For using unconditionally secure authentication code to prevent pollution attacks, the main innovation of our scheme is that it can be used for multi-source network coding systems. Our scheme is based on the method [9] of Frederique et al, who proposed an authentication code against pollution attacks for single source network coding.

• II.  Background

A.    Secure network coding

As network coding allows intermediate nodes to encode the received messages, the result is that network coding is very vulnerable to pollution attacks. Pollution attacks, which consist of injecting malicious messages in the network. If the networks don’t have the detection for integrity and origin of the received messages, the polluted messages can quickly propagate into the whole network and infect a large proportion of messages, because they will be transmitted by the downstream nodes. So the secure network coding is very essential. There are two methods to design secure network coding, one is based on computational hypothesis, and the other is on theoretic strength. Gkantsidis et al. proposed a scheme [3] for network-coded content distribution allows intermediate nodes to detect malicious messages injected in the network; it uses a homomorphism hash function to generate hash values of the encoded blocks of data. While it requires fresh keys for each file, so the scheme is not practical. Charles et al. designed a homomorphism signature scheme [4] based on Weil pairing over elliptic curves, but the idea is conditionally secure. Zhao et al. used a standard signature scheme [5] based on the hardness of the discrete logarithm problem, besides, it also requires fresh keys for each file, and it can’t support multi-source network coding. All in all, the previous expatiation methods mainly relay on computational hypothesis, these schemes are conditionally secure; besides, they can’t support multi-source situation. While the idea based on theoretic strength, unconditionally secure authentication code, provide another method to design secure network coding which is robust against an attacker even it has unlimited computational resources.

B. unconditionally secure authentication code

In order to prevent pollution attacks, previous methods about secure network coding, mainly based on computational hypothesis, while the idea of designing secure network coding on theoretic strength is proposed less. So the way of theoretic strength provides another method to achieve secure network coding. Unconditionally secure authentication code promotes the development of multi-receiver authentication code [6] [7] [8]. Frederique et al. proposed a method [9] to prevent pollution attacks for single source node network coding, the scheme introduces unconditionally secure authentication code in multicast network, and it is robust against pollution attacks. Intermediate nodes can verify the integrity and origin of the messages received without having to decode the encoded messages, and will discard the messages that fail the verification. By this way, the pollution is canceled out before reaching the destinations.

III. Multi-source network coding model

Yan et al. [10] proposed a multi-source network coding model example in multi-source network coding situation, each source node transmit message separately. The multi-source network is modeled by a directed graph G = ( E , V ), where E is the set of links and V is the set of vertices in the network. Suppose there are n source nodes, each source node transmit only one message vector to the intermediate node. In this situation, each edge of the graph carries a symbol f ( e ) ∈F q at a time. For a node of the graph, the symbols on its outgoing edges are linear combinations. Thus to any receiver node, if it gets message vector t 1…. t n from n source nodes, then it has the following expression on each edge;

n f (e) = E gi( e) ti i=1 (i)

Where the coefficients g i ( e ) describes the coding operation. The vector g ( e )=[ g 1 ( e )… g n ( e )] is thus called the global encoding vector along the edge e . So to a receiver node, if it gets message from n source nodes, with it have n incoming edges, there is a following matrix equation:

G

t 1,1

t 1,2

t 1, N

A

Г f ⁽ e i ) ) Г g i ⁽ e i )

к f ( e „ ) ) ( g i ( e n ) l

At the same time, the

^gn ⁽ e i ) Y t 1 )

M M gn (en ) Л tn )

G D

t i

A

^к t n ⁾ (2)

symbols f ( e ) flowing on each

edge e can be packetized into vectors y ( e )=[ f 1 ( e ),., f N ( e )], and likewise, the message vector t i from each source also can be grouped as x i =[ t i , ,., t i,N ]. So the above equation can be rewritten as:

Г y ⁽ e i ) ) Г g i⁽ e i ) L g n ⁽ e i ) Y ^x i )

к У ⁽ e n ) ) ( g i⁽ e n ) L g n ⁽ e n ) A x n )

=      к t n ,i

Where x 1 , x 2, …, x n

t n ,2    L t n,N ) (3)

is each source node which sends

one message a time to the receiver node. So to any node v i in the multi-source network, with its incoming edges

e i 1 … e ih . Each source node is sends one message a time to the receiver node. So to any node v i in the multi-source network, with its incoming edges e i 1 … e ih , it has below matrix equation:

^Г У ( e i i ) ) ^Г g i⁽ e i i ) L g n ( e i i ) Y x i )

к y ⁽ e ih ) )   к g i⁽ e ih ) L   g n ⁽ e ih ) Y x n ) ₍₄₎

IV. Unconditionally Secure Authentication Code For Multi-source Network Coding

A. Proposed authentication scheme

• 1)    Private key generation

A trusted authority randomly generates polynomials for each source node, to source node S 1 ; it has M +1 polynomials

P 0 ¹( x ),....., P M ¹( x )

,

And likewise, source node S n has M +1 polynomials

P 0 ⁿ ( x ),....., P M ⁿ ( x )

,

And choose V difference variants x 1 … x V ∈F q , these polynomials are of degree k -1, the specific situation is made as follows:

P i ^{i (} x ) = a ‘o + a ii x + a *2 x ² +.....+ a ‘, k - i x k ⁱ (5)

P" ( x ) — a n ₀ + a n x + a n x ² ++ a", x kk - ⁱ i                  i 0          i i            i 2                           i , k - i

Where i =1… M

2) Private key distribution

The trusted authority gives as private key to each source node, for source node S 1 , its private key is

₍ P 0 ¹( x ),

, P M ¹ ( x ) ₎

. And likewise, the private key

Pⁿ ( x ) Pⁿ ( x )

for source node S n is ( ⁰ ,, ^M ) . At the same time, the authority distribute private key for V verifier nodes. Suppose R_i is the i th verifier, then its private key is defined as follows

₍ ( 2 0 P 0 ( x i ) + 2 0 P o ²( x i ) ++ 2 n P o ⁿ ( x i )), ( A M p M ( x i ) + 2 M P M ( x i ) ++ 2 M P M ( x i ))

3) Authentication code generation:

Suppose such a situation that each source node sends message vector one time, the sequence is made as a1,…,an, each message has the length l, then compute the following polynomial:

11    22        nn

A ai ^{( x} ) = ^{[ 2} 0 ^P 0 ^{( x} ) ^{+ 2} 0 ^P 0 ^{( x} ) ⁺.....^{+ 2} 0 ^P 0 ^{( x )]}

+ a i [ A 11 P 1 ¹ ( x ) + A 2 Р 1 ( x ) +.....+ Aⁿ n P₁ⁿ ( x )]

+ a i⁴ [ A 2 P 2 ( x ) + A 2 P ₂²( x ) ++ A 2 P 2 ( x )] + + a _t ^{4 (} M ^{- 1)} [A m P M ( x ) + A m P M ( x ) ++ A m P M ( x )] (7) Which forms the authentication code of each message, i=1… n

• 4)    Encoded message transimittance

In our multi-source network, as previous description, to a verifier node R i , if it has n incoming edges, gets the message sequence from the source nodes.

As a 1 … a n , thus the final formation of the packet likes this: x_i =[1, a_i , A_ai ( x )], i =1… n , so it can write as follows:

f y(e 1) 1 M к y (em) J

f g i⁽ e j L g n ⁽ e j Y¹

I g 1⁽ ei n ) L g n ⁽ e in ) A¹

a ₁

^Aa 1⁽ x )

M

A an ( x ) J

While verifier node R i has the private key

( A P ;1 ( x.) + A ; P o ²( x i ) ++ AX ( x , )),

( A M P M ( x i ) + AM P M ( x i ) ++ a m p m ( x i ))

So, to each edge e k of the verifier node, k= 1, 2... n separately. Compute the following polynomials as below:

n

A o = [ A P o ¹ ( x i ) +.....+ a ; P ; ( x, )] £ g j ( « „ ) (9)

j = 1

A m = [ A M P M ( x i ) +.....+ A M P M ( x , )]*

q ( ^M - 1)

L gj(ek)aj j=1                      (10)

Meanwhile, it has following equation:

n

L g j ⁽ e k ) A aj⁽.^x )

j = 1                     =

n

L gj (ek ) 1 P1/ X          + +йпРп(хА j=1        { [Ao Po (x) + Ao Po (x) ++ Ao Po (x)]

+

• a , [ A 1 P ¹ ( x ) + A 2 P ² ( x ) ++ A n pⁿ ( x )] ^{j 1 1              1 1                        1 1}          +^..... +

aj¹ ( ^{M - 1)} [ A M P M ( x ) + A M P M ( x ) +.....+ A M P M ( x )] }

From the above equation, we can learn that the authentication code of after-encoded message is the formation of the combination with source authentication codes, thus it does not need extra cost to compute the authentication codes of the encoded messages.

• 5)    Authentication process

When an intermediate verifier node receives the message, then it makes the authentication for the message. So to the verifier node R i , bases on its private key and x i , it can compute A 0 , A 1 ... A M while it also can get the equation

n

^B = L g j⁽ e k ) ^Aaj⁽ x i )    ⁽¹²⁾

j = 1

If A 0 + A 1 +…. + A M = B , then receives the message, otherwise, it discards the message.

• 6)    Decodding message received

Verifier node receives the message that passes the authentication, because the after-encoded message is the formation of the combination with source authentication codes, the encoded message can be decoded by Gauss Eliminate.

B.    The analysis of authentication scheme efficiency

For the authentication scheme, the analysis is made as follows: communication cost, computational cost and storage cost.

Communication cost: The cost mainly relies on the size of the authentication tag A_ai , as the length of tag is nkl , so the computation complexity is O ( nkl ).

Computational cost: The cost involves computing and appending the authentication code at the source, and verifying the authentication code at some intermediate nodes and at the destinations. On the one hand, cost at the source: For a message a_i , in order to generate authentication code, source node need to compute the following polynomial:

Aai(x)= [a; P;1( x)+a; P;2( x)++ax (x)] + ai [A1P1 (x) + A2 P12 (x) + + AnP1n (x)] + ai4 [A2 P2 (x) + A2 P2 (x) + +A2 P2n (x)] +…..+

( M -1)

a^   [ A M P M ( x ) +A M P , (.x ) + .... + A M P M ( x )] (13)

Which involves n ( M -1) l exponentiations, besides, it includes nkMl multiplications; On the other hand, Cost at the verifying nodes: For a verifying node R i , it has to do two things to check the authentication code. First, it has to compute the following expressions:

n

A o = [^ 0/0 ( x ) + A ; Р 2 (x ) + .... + A ; P ( x i )] S g / ( e » ) (14) j = 1

n

A = [ A 1 /P (, x ) + A F f ix i ) + .... +A P ( x^ L ^ e* , (15)

j = 1

f n

q

A 2 = [ A 2 P₂(x ) +A 2 P 2 (x ) + .... +A 2 P 2 ( x )] L gMe kk ) a  (16)

к j =1           J

+ VM ( X )

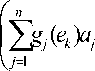
qq ^{M l}-

J

Suppose in a multi-source network, it has two source nodes, the verifier node R 1 receives two messages at a time. Thus a node R ₁ has received the following vector:

^f y ^{( e} 1 ) )

Which contains n ( M -1) l exponentiations, and also include n(M +1 )l multiplications; Second, it has to compute B . s ince the polynomial is of degree k -1, so to x i , j = 2,, k — 1 , it involves n ( k -2) l exponentiations, to X^j j , j = 1, , k — 1 , it contains n ( k -1) l multiplications

• Storage cost: The cost of storing private key at the source is O ( n ( M +1) lk ); while the cost of storing private key at the verifying nodes is O ( n ( M +1) l ).

C. The analysis of authentication scheme security

For this scheme, our object mainly prevents malicious node to make a substitution attack, that is, to send a fake message such that a node which checks the authentication code, we consider two situations. One is for a single malicious intermediate encoded node, and the other is a group of malicious intermediate encoded nodes.

1) Against one malicious node:Suppose that a malicious node Vi has h incoming edges, its received vectoris thus has the following equation:

( У ^{( e} i1 ) )   ( g 1⁽ en) L g h ⁽ en) Y ^X 1 )

( У ⁽ e 2 ) J

With previous description, we can get

Consider the node is malicious, instead of checking the authentication code it actually wants to make a substitution attack. Since we have that:

A 1 ( X ) Z AP ( - )+№N [ XP(x)+ZР (.ф a , W 1 (x)+ZPx )]

= ^{[ Z} 0^{( a} 00 ^{+ a} 01 ^X ) ^{+ Z} 0^(a 00 ^{+ a} 01 ^{x )]}

11   1    22   2

₊ a ₁[ Z ₁( a ₁₀ + a 11 x ) + X 1 ( a ₁₀ + a 11 x )]

+ a 1 [ z ? ( a 20 + a 21 x ) + A ? ( a ?q + a 21 x )]

11   22    11   22     11   22  2

^{[( X} 0 ^a 00 ⁺ X q ^a 00 ) ^{+ (} A ^a 10 ⁺ A ^a 10 ) ^a 1 ^{+ (} ^ 2 ^a 20 ⁺ ^ 2 ^a 20 ) ^a1 ^] +

11   22    11   22     11   22  2

x [( x q a 01 + X q a 01 ) + ( X 1 an + X 1 an) a 1 + ( X , a 21 + a ? a 21 ) a 1 ]

₌. b 10 ^{+ xb}11

A ,( x )=[/ P (x)+№x)]HAIp(x)+XI1^t(x)^+a 2² [A 2 P 1 (x)+X 2 T2^z( x )]

= [ X 0 ( a Qq

1    22

^{+ a} 01 ^x ) ^{+ X} q ^{( a} 00

^{+ a} 0²1 ^x )^]

( y ⁽ e ih ) J  ( g 1⁽ e ih ) L g h ⁽ e ih ) A ^xh J

11   1    22   2

+ a 2 [ X 1 ( a 10 + a ц x ) + X 1 ( a 10 + a ц x )]

₊ a ₂²[ A *₂ ( a 2 ₀ + a 21 x ) + X 2 ( a 2 ₀ + a 21 x )]

f g 1 ⁽ e i 1 ) L g h ⁽ e 1 1 ) Y¹

a 1    ^A a 1 ^{( X} ) )

= I g 1 ⁽ e ih ) L g h ⁽ e ih ) A¹   a h    ^A ah ^{( X} ) J  (18)

If we write

^Aaj ^{( X} ) = ^bj0 ^{+ b}j1^{X ++ b}j,k - 1 ^Xk ^{- 1} (19)

So we have that for all incoming edges e m , m = i 1 … i h hh

Zgj (em )Aaj (x) = Zgj (em Xj + ЬЛX +.....+ Ak— j =1                        j =1

[(^ 0 a Qq + X a q²q ) + (X a\ o + X ? a^ a ? + ( X ? a 2q + X ? a 2q ) a ? ²] +

11   22    11   22     11   22  2

x [( A q a q1 + X q a 01 ) + ( X 1 an + X 1 an)a ? + ( X ? a ?1 + a ? a 21 ) a ? ]

=, b ₂₀ + xb ₂₁

We can rewrite:

g 1⁽ e 1 ) ^Aa 1^{( x} ) ⁺ g 2⁽ e 1 ) ^Aa 2^{( x} )

= g 1⁽ e 1^{)( b} 10 ^{+ xb} 11 ) ⁺ g 2⁽ e 1^{)( b} 20 ^{+ xb} 21 )

= g 1 ⁽ e 1 ) ^b 10 ⁺ g 2 ⁽ e 1 ) ^b 20 ^{+ x (} g 1 ⁽ e 1 ) ^b 11 ⁺ g 2 ⁽ e 1 ) ^b 21 )

x^{k 1}

)

,                 .             ,                    k - 1

C n +c ,% +.....+ c , ,x

= ^m 0     m l              m , k — (20)

So malicious node knows c mi , where i =1, 2... k -1. For each incoming edge of the malicious node, it can obtain the following system of linear equation: AG = C , where A is a matrix with k X( M +1 ) , contains the coefficients of the private key, C is a matrix with k X h , which known to the malicious node. For the authentication scheme to be secure, we at least need ( M +1)> h .

For this situation, we will give an example.

The malicious node thus knows c 10 = g 1 (e1)b10 + g2 (e1 )b20

, c 11 = g 1( e1) b11 + g 2( e1)b 21

Alternatively, we can rewrite:

g 1⁽ e 1 ) ^Aa 1^{( x} ) ⁺ g 2⁽ e 1 ) ^Aa 2^{( x} )

₌ g ₁( e ₁)

11   22    11   22     11   22  2

^{[( X} 0 ^a 00 ^{+ a} q ^a qq ) ^{+ ( A} 1^a10 ⁺ A 1 ^a 10 ) ^a 1 ⁺ ( Z ? ^a 20 ⁺ Z ? ^a 20 ) ^a 1 ^]

₊ g ₁( e ₁) _×

x [( 2 a 1₁ + 2 0 a ^)+ (2 1 4 + 2 2 a ^) a ₁ + (2 2 a ^ + 2 2 a ₂ ² ₁ ) a ₁ ² ]

₊ g ₂( e ₁)_×

[( Л 0 a 0o + 2 0 a 0o ) + ( 2 1 4 + 2 2 a ^) a 2 + ( 2 2 a 00 + 2 2 a 20 ) a 2 2 ]

₊ g 2 ( e 1 ) _×

11   22    11   22     11   22  2

x [( 2 a 01 + 2 o a 01 ) + ( 2 1 a ^ + 2 1 a ^) a 2 + ( 2 2 a 21 + 2 2 a 21 ) a 2 ]

= ( 2 0 a 0o + 2 0 a 00 )( g . ( e 1 ) + g ₂( e j)

+ ^² 1 a 10 ^{+ 2} 1 a 10^{)( g} 1^{( e} 1 ) ^a 1' ^{+ g} 2^{( e} 1 ) a 2 )

+ ^{( 2} 2 a 20 ^{+ 2} 2 a 20 ^{)( g} 1⁽ e 1 ) a 1 ^{+ g} 2⁽ e 1 ) a 2 )

₊ x [( 2 0 a 0! + 2 0 a 2₁ )( g , ( e ^ + g ₂ ( e ^)

+ ^{( 2} 1 a 11 + ² 1 a 11 ^{)( g} 1⁽ e 1 ) a 1 + ^g 2⁽ e 1 ) a 2 )

+ ^{( 2} 2 ^a 21 ^{+ 2} 2 a 21^{)( g} 1⁽ e 1 ) a 1 ^{+ g} 2⁽ e 1 ) a 2 ^)]

Since the malicious node knows:

g 1⁽ e 1 ) ⁺ g 2⁽ e 1 )

g 1⁽ e 1 ) a 1 ⁺ g 2⁽ e 1 ) a 2

g 1⁽ e 1 ) a 12 ⁺ g 2⁽ e 1 ) a 2 2

Because the malicious has two incoming edges, it can get the following equation:

2a . + 2 0 a^ 2 1 4 + 2 2 4 2a 0₁ + 2 0 0 2! 2 1 + 2 2 a 2₁

2 2 a 20 + 2 2 a 20'

2 2 a 21 + 2 2 a ^ ^J

G =

² c ⁰

V ^c 11

c20

^c 21 /

(21) Where

G =

(    g 1 ^{( e} 1 ) ⁺ g (e ^e 1 )

g 1 ⁽ e 1 ) a 1 ⁺ g 2 ⁽ e 1 ) a 2

V g 1 ⁽ e 1 ) a 12 ⁺ g 2 ⁽ e 1 ) a 2 2

g 1 ⁽ e 2 ) ⁺ g 2 ⁽ e 2 )

g 1 ⁽ e 2 ) a 1 ⁺ g 2 ⁽ e 2 ) a 2

g 1 ⁽ e 2 ) a 12 ⁺ g 2 ⁽ e 2 ) a 2 2 >

We can learn that G is a 3X2 matrix , thus it satisfy the security condition . otherwise, if only need two polynomials to create the authentication code, then the matrix G would be a 2X2 matrix, and thus could be very likely invertible, so the malicious node can recover the secret coefficients of the source private key, in other word, the authentication is not secure.

M +1 ^ h 1 + h 2 +^+ h_K (25)

We consider a situation where some of the nodes who are given the private keys to check the authentication could be corrupted, for we consider that K nodes v 1 ,…,v K collaborate, thus we assume the worst case, namely that all of them actually have the private key:

(( 2 0 P 0¹ ( x_z ) + 2 2 P4X i ) +.....+ ²Х ( X i )),.....

(2_MP M ( X i ) + 2_MP M2 ( X i ) ++ 2 M P M ( X i )))

Where i =1, 2,…, K .

Since the values x1,…,xT, the group of adversaries can get the following equation with their knowledge of the private key, namely XA=P, where f1

x ₁

X =

x ₂

k - A

^X 1

x ₂ k ¹

л                            k -1

V ^{1 X}K  L ^XK 2 (26)

where the K X k matrix X contains the public key values, where the k X (M+1) matrix A contains the coefficients of the private key, where the k X(M+1) matrix P contains the private key of the malicious nodes. Since the degree of the polynomials is k-1, namely K can be at most k-1, otherwise from the knowledge of only the private and public keys, the group of malicious nodes can recover the source nodes private key. The following description will prove that suppose the adversaries know the private key and the one gathered from all the received vectors, the adversaries still can not do better than guess the source nodes private key.

The following description will prove that the adversaries know the private key and the one gathered from all the received vectors, the adversaries still can not do better than guess the source nodes private key.

Lemma: There exist q matrices A with coefficients, such that: AG ^’ = C ^’ , XA = P

Where A is the matrix of k X( M +1),

X is the matrix of ( k -1) X k,

G is the matrix of ( M +1 ) X H,

C is the matrix of k X H,

P is the matrix of (k-1) X(M+1), and H=h1+h2+…. +hK.

Proof: Since the matrix G is of the form

2       ”

E g j⁽ e i)

j = ¹

-A

E gj( ei) aj j=1

v (   4 q ( ^M -¹)

E g j ⁽ e i) a j

V j = 1

n                ^

E g j ( e iH )

j = ¹

E gj( еш) aj j=1

V t a   q ( ^M - ¹ )

L  Egj(eiH)aj j=1                        2

For any invertible matrix D , we have that

AG ’ =C ’ ^ AG ’ D = C ’ D   (27)

We can rewrite that: there exists an invertible matrix D , such that G ^’ D is of the Vandermonde like form:

( 1

Y 1

q

Y 1

1 )

Y h

q

YH q (M-I)              q (M-I)

IYi       L  Yh)

Specially, if all the coefficients of the first row of G ^’ are not zero, we can rewrite as:

nn

D = dag(£ gj (e„)) ,,(£ gj (e h))-1) j=1                        1-1(28)

So the problem change into another formation, namely AG = C , XA = P with G satisfy the Vander monde form.

Firstly, we solve a homogeneous system of equation: AG’=0, XA=0.(29)

We define f ( x , y ) = (1, x … x^{k -1} ) A (1 y … y^{q ( M -1)} ) (30)

Since A contains f ( x , y ) in two indeterminate x and y , then it exists a polynomial f(x,y) whose roots are

^X 1, ’ ^Xk ^{- 1} and ^{Y 1}, ’ ^{Y h} , thus we can get XA =0 in x = x 1 … x k , likewise, to AG =0. We can get corresponding y , since these coefficients of the matrices in F q also satisfy the equation, this gives q suitable matrices. So based on homomorphism, the lemma can be proved.

Proposition: The above scheme is suitable for multisource network coding situation, and it uses an unconditionally secure authentication code to prevent pollution attacks. The scheme is robust against a coalition of up to k -1 adversaries in which every key can be used to authenticate up to M messages.

Proof: To make a substitution attack, the k -1 malicious nodes want to generate a message such that it is accepted as authentic by the receiver R i that they are trying to cheat, but this message is bogus, then these malicious nodes need to guess their private key: ( ( Л 0 P j( x , ) + 2 0 P _o4 x , ) +.....+ W ( x , )), ( 2 M P M ( X , ) + 2 M p M ( x , ) +.....+ 2 M P M ( x , )))

And choose a polynomial:

A a ( X , )' = [ 2 0 P ( X , ) + 2 0 P ( X , ) +.....+ W ( X , )]

+ a^q [ 2 1 P 1¹ ( x , ) + 2 2 P 1² ( x , ) +.....+ 2 П Р 1 n ( x , )]

+…..

+ a q ⁽ M ^{- 1)} [ 2 1 м Р М ( x , ) + 2 M P M ( x , ) ++ 2 M P M ( x , )]

These malicious nodes can get the following equation by seeing the message transmittance:

A G =C ²¹ k x ( M + 1)'^J( M + 1) x H    k ^ k x H

useless. While if the matrix exists, then there are q matrices, namely, there are q different ( M +1 ) tuple of polynomial ( ⁰ ( x ) ,....., ^M ( x ) ) , likely to be the source nodes private key. Thus the probability of the guess is 1/ q .

V. Conclusion

In this paper, we proposed an unconditionally secure authentication code scheme that is suitable for multisource network coding; our scheme is robust against an attacker even it has unlimited computational resources, for our scheme is based on theoretic strength. Besides, the authentication scheme is robust against pollution attacks either from outsides or coalition of k -1 malicious insiders. In multi-source network coding, intermediate nodes can verify the integrity and origin of the messages received without having to decode, and detect and discard the messages that fail the verification. By this way, the pollution is canceled out before reaching the destinations. Besides, in our paper, we compare several schemes with our method, the specific result is listed as the following table. From the table, we know that our scheme supports multi-source network coding, and also is immune from the savage attack. Since the research of multi-source network coding was studied fewer, our scheme about the security analysis is not perfect; it needs still to be improved on.

Table 1. The comparison of several schemes

Scheme	Multi-source support	Savage attack limitation
Yu’s[11]	No	a 22
Zhao’s[5]	No	b 22
Charles’s[4]	No	c 22
Frederique[9]	No	None
Our scheme	Yes	None

Where: a = d stands for the RSA private key in [11] b = a n Stands for the private key in [5] c = sn Stands for the private key in [4]

The results of savage attack limitation are got by the Birthday Paradox [12]

Acknowledgment

This research was supported by the National Natural Science Foundation of China (under Grant No.60672137).