The speed electromagnetic wave propagation in the snow-ice underlying surface

Цитирование: Малышев, В.А. Скорость распространения электромагнитной волны в снежно-ледяной подстилающей поверхности / В.А. Малышев, В.Г. Машков // Журн. Сиб. федер. ун-та. Техника и технологии, 2021, 14(3). С. 332–346. DOI: 10.17516/1999–494X-0313

well as in conditions raised snow by its rotating screw [1]. The need for such a landing may be caused, for example, by cargo delivery, search and rescue operations, or evacuation of the wounded.

When measuring the depth snow and the thickness ice cover by radar, its accuracy will depend on the accuracy measuring the time delay and the speed propagation an electromagnetic wave (EW) in a medium other than the speed propagation EW in a vacuum c = 2,9979245840 8 m/s, depending on its dielectric constant. A snow-ice surface is a three-component medium that is a mixture ice with water and air inclusions [2]. In turn, the dielectric permittivity the snow-ice underlying surface, depending on the density and proportion water content, will vary significantly. Since, for example, the real part the static permittivity melt water is e m _{w s} = 87,9 [2, 3], and dry dense ice (without air inclusions) ε^′ di = 3,20±0,02 [2-5].

The value the permittivity dry snow cover is between ice and air e a = 1 depending on the density, as well as the preferred orientation and form inclusions ice and air in the snow. Depending on the shape the crystals, snow may have different physical properties. The snow density varies for open areas, forests, and melting snow and is in a very wide range of 10...700 kg/m³, which affects all snow characteristics.

Denser, solidified granular and partially recrystallized, usually long-term snow (firn), or rather the intermediate stage between snow and glacier ice has a density of 450 ... 800 kg/m3 due to interconnected ice grains [6].

Since the density snow on the height the snow cover is very heterogeneous and is determined by the depth and duration its occurrence, the density snow cover is an average value.

In the European part of Russia, the average density snow cover at the end the winter period in the Northern regions is within 220...280 kg/m3, in the middle zone – 240...320 kg/m3, in the South – 220...360 kg/m3, the wider limits are explained by intermittent thaws. The presence water and water vapor (moisture) significantly increases the density snow cover. Melting snow has a higher density value, so in most cases at the beginning melting it is within the range 180...350 kg/m3, changes at the height melting to 350...450 kg/m3, at the end melting it reaches 600 kg/m3 [6].

Property water

The static permittivity water is great importance, which is explained by the chemical structure the H 2 O molecule. The orientation degree freedom molecular dipoles and their rotation largely determine the electrical properties water [7]. Dipoles are randomly oriented in the absence an external electric field (EF), and the total EF they create is zero. The action the EF contributes to the reorientation the dipoles, leading to its weakening. In all polar liquids, this happens, but water is able to weaken the external field by almost 80 times. With increasing frequency, the dipoles do not keep up with the external EF and stop reacting to it, while the value the water’s permittivity decreases to 4...5 for frequencies greater than 10¹² Hz. In this case, the permittivity is determined only by the atomic-molecular redistribution the electric charge characteristic all substances.

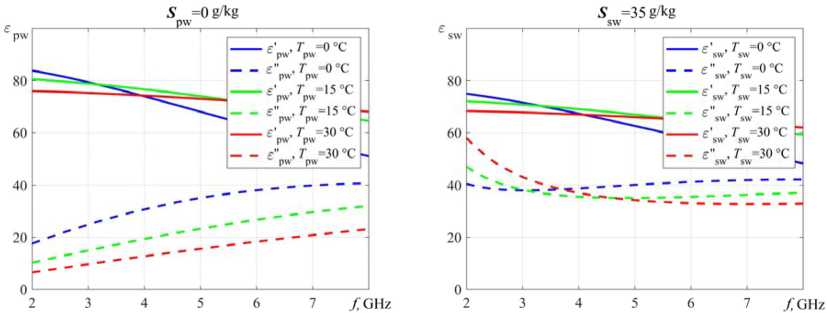
According to [7, 8], the complex relative permittivity pure water ε pw (Fig. 1а) depends on the frequency / (GHz) and temperature T _pw (°C), e _pw defined by the formula (1), real part e _pw - (2), imaginary part ε^ʺ pw – (3):

ε pw

= ε _pw – jε _pw;

;

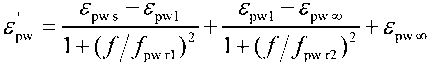
_ ^/'/c/pwrl X^pws" £pwl )

! + (///,», .)’

Zpw r2 X^pwl ^pw oo 1+(///,.„)’

where: ε pw s , ε pw1 = 0,0671 ε pw s , ε pw ∞ – static, current, and dynamic permittivity pure water, respectively; f pw r1 and f pw r2 = 39,8 f pw r1 – Debye relaxation frequencies.

Since water is a good solvent, in nature certain salts are almost always dissolved in it, that is, there are positive and negative ions in the water. Water is weakly dissociated under normal conditions and the concentration of protons (hydroxonium H 3 O⁺ ions) and hydroxyl OH^-ions is 0,1 μmol/l [9]. Electrical conductivity, as a numerical expression the ability an aqueous solution to conduct an electric current natural water, is determined mainly by the concentration dissolved mineral salts and temperature. Natural waters are mainly solutions mixtures strong electrolytes, the mineral part which is made up ions Na⁺, K⁺, Ca²⁺, Cl^-, SO 4 ^2-, HCO 3 ^-, which determines the electrical conductivity. Other ions, for example, Fe³⁺, Fe²⁺, Mn²⁺, Al³⁺, NO 3 ^-, HPO 4 ^-, H 2 PO 4 ^-they do not significantly affect the electrical conductivity if they are contained in water in small fractions.

The normalized values mineralization approximately corresponds to the specific electrical conductivity 2 μSm/cm (Sm – Siemens, the inverse Ohm) (1000 mg/dm³) и 3 μSm/cm (1500 mg/dm³) for chloride (in terms of NaCl) and carbonate (in terms of CaCO 3 ) mineralization [9]. The specific electrical conductivity water characterizes the salinity fresh water (salinity seawater) depending on the temperature, concentration and nature ions, for distilled water T pw = 25 °C respond 2...5 μSm/cm, precipitation – 6…30 μSm/cm and more, in highly polluted air mediums, river and fresh lake waters 20…80 μSm/cm.

The salinity sea water varies within: for the Baltic sea S pw = 10…12 g/kg (Gulf of Finland S sw = 2…3 g/kg, in the Danish Straits S sw = 20 g/kg at the surface the sea and S pw = 30 g/kg near the bottom); for the red sea S sw = 40…42 g/kg; for the Dead sea S sw = 300…310 g/kg (before S sw = 350 g/kg). Salinity the world ocean water S sw = 30 g/kg.

а)                                                             b)

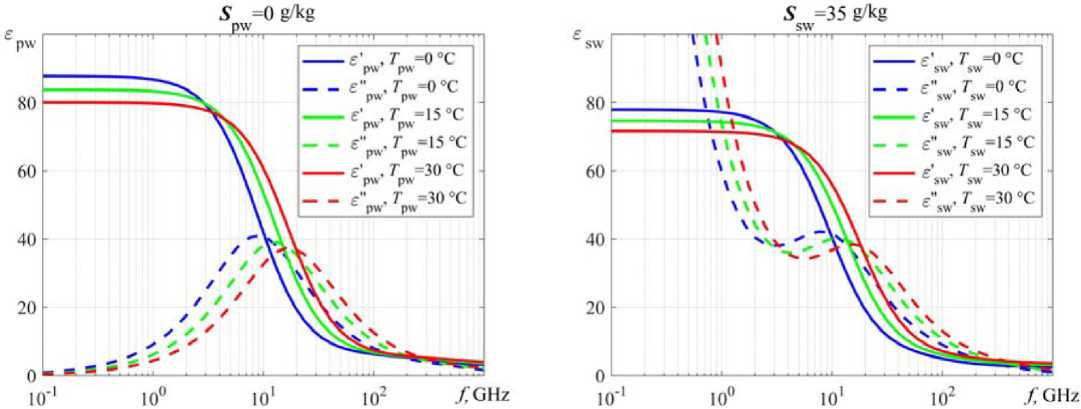
Fig. 1. Dependence the complex relative permittivity: a – ε pw pure water S pw = 0 g/kg by (1-3); b – ε sw sea water S sw = 35 g/kg by (4-6), from frequency f at T r = 0; 15; 30 °C

According to [8], the complex relative permittivity seawater ε sw (Fig. 1b) depends on the frequency f (GHz), temperatures T sw (°С) and salinity S sw (g/kg or ppt), ε sw defined by the formula (4), the real part ε^′ sw – (5), imaginary part ε^ʺ sw – (6):

ε sw

= ε _sw – jε _sw;

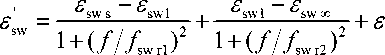
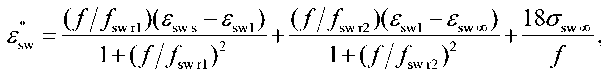
where σ sw s – the conductivity seawater is dependent on salinity sea water S sw and temperature T sw . By S sw = 35 g/kg and T sw = 0 °C σ sw s = 2,9036.

As can be seen from Fig. 1 the value the complex relative permittivity water with increasing salinity S sw and temperature T decreases. It should be noted that the water density reaches its maximum values 999,972 kg/m³ at temperature T = 3,8…4,2 °С [10], as the temperature decreases further, the density decreases. This temperature dependence density is typical only for water.

Properties the ice sheet

The electrical conductivity ice and snow is many times less than that water. The presence various impurities in water has a significant effect on its electrical conductivity and practically does not affect the electrical conductivity ice. Partial dissociation molecules into H⁺ and OH-ions determines the electrical conductivity chemically pure water. Movements of H⁺ ions (proton jumps), which create two types defects in the ice structure: ionic and orientation, have a major influence on the electrical conductivity water and ice. In the first case, the proton jumps along the hydrogen bond from one H 2 O molecule to another, resulting in a pair ion defects H 3 O⁺ and OH^-, and in the second – to the neighboring hydrogen bond in one H 2 O molecule, while a pair orientation L and D-defects occurs [9, 11].

As the temperature increases, the electrical conductivity increases exponentially, which distinguishes ice from metal conductors and puts it on a par with semiconductors. Ice is usually very clean chemically, even if it has grown from contaminated water or solution, because it has a low solubility impurity in the structure. When freezing at the crystallization front, the impurities are pushed into the liquid, do not enter the structure ice, so the newly fallen snow is white, and the water from it is exceptionally clean. Ice is a proton semiconductor, since the charge carriers are disordered protons and there are no free electrons in it, as in metals [9, 11].

According to [8] the complex relative permittivity dry ice ε di consisting frozen water, i.e. T ≤ 0 °C

ε d _i = ε d _i – jε d _i.                                                                                   (7)

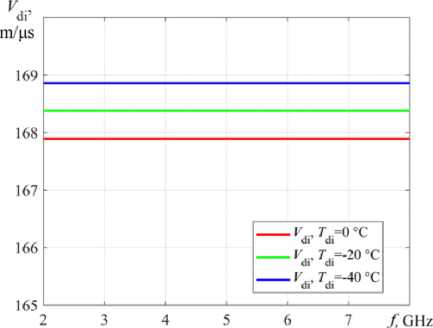
The real part the complex relative permittivity ε^′ di depend on temperature T di and it doesn’t depend on the frequency f . For dense ice when T di = 0 °C ε^′ di = 3,19 ± 0,04 [12, 13], a in the temperature range T di = 0…–20 °C, characteristic Subpolar and warm glaciers, this dependence is described by the equation ε^′ di = 3,1968 ± 0,061 T di [12, 13], according to [8]

ε^′ di = 3,1884 + 0,00091 T di ,                                                       (8)

an imaginary part the complex relative permittivity ε^ʺ di depend on temperature T di and the frequency f [8]:

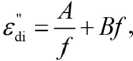
where:

Л= 0,00504 + 0,0062

300 4+273,15

exp -22,1

300 4+273,15

;

в_ 0,0207 ”4+273,15

exp--

( 4+273,15

exp-- ( 4 + 273,15

-1

, + 1,16x10 п/2+ехр( 9,963 + 0,03724).

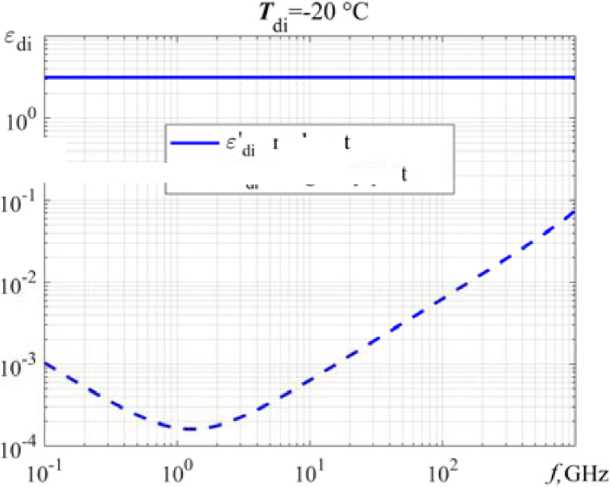
Real ε^′ di (8) and the imaginary ε^ʺ di (9) parts the complex relative permittivity dry ice are shown in the Fig. 2 [8] for T di = –20 °C from frequency f .

real part

--£"di imaginary part

Fig. 2. Dependence the complex relative permittivity dry ice ε _di by (7-9) from frequency f at T _di = –20 °C

When the ice is wet T wi = 0 °C, its grains are surrounded by water. Considering ice grains as spherical inclusions in water, the Maxwell-Garnett dielectrics mixing formula is applicable [8]:

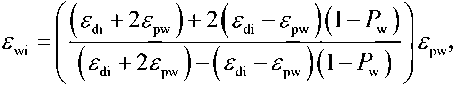
where ε wi , ε di , ε pw – complex relative permittivity wet ice, dry ice, and clean water, respectively; P w – volume fraction water (m³/m³). Each part equation (10) is a function the real and imaginary parts the complex relative permittivity dry ice and the corresponding parts water.

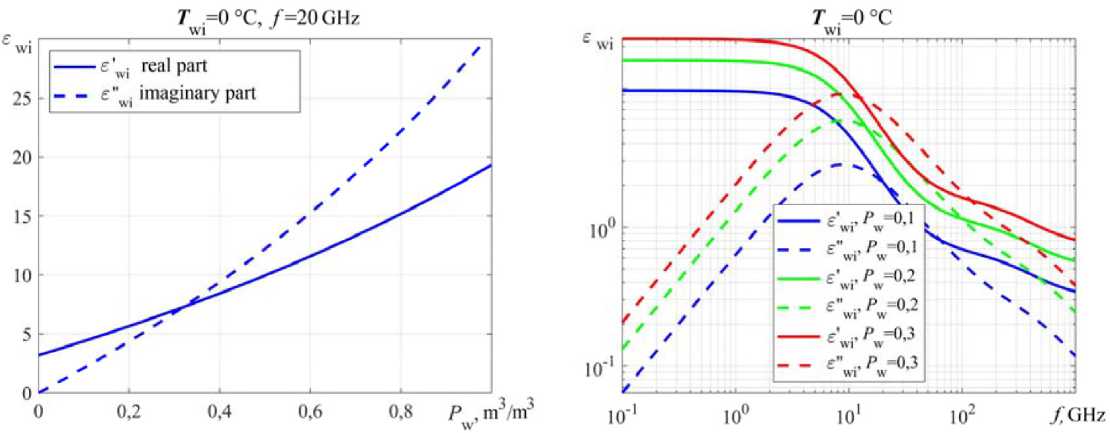
Real and imaginary parts wet ice according to (10) at f = 20 GHz and T wi = 0 °C (Fig. 3а) depending on the water content P w and from f (Fig. 3b) with a fraction the water content P w = 0,1; 0,2; 0,3 shows a significant increase in indicators with an increase in the share water content.

а)

b)

Fig. 3. Dependence the complex relative permittivity wet ice ε _wi by (10) depending from: a – the proportion liquid water content P w at f = 20 GHz; b – the frequency f with the proportion liquid water content P w = 0,1; 0,2; 0,3 at T wi = 0 °C

The speed propagation an electromagnetic wave in the operating frequency range

In General, the real subsurface structures medium is largely not uniform, so it is difficult to take into account their parameters when modeling without averaged values for subsequent studies. The structure the medium an unprepared site for landing on a snow-ice underlying surface, as a rule, consists of several layers, it can be snow, firn, ice, clean water and sea water.

The depth penetration EW δ d in work [8], defined as the depth at which the field strength amplitude within the medium falls to 1/ e (about 37 %) from its original value on the surface

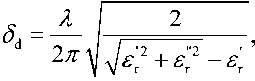
where λ – the wavelength the probing signal; ε^′ r and ε^ʺ r – the real and imaginary part the dielectric constant the medium, respectively. One the criteria for selecting the frequency range is the depth penetration (11) into the snow at frequencies 2…8 GHz about 10 m and a resolution about 4 cm in the ranges C…S (3,75…15 cm), this allows you to get a reflected signal from the interface between the medium «air-snow», «snow-ice», «ice-water».

The speed propagation EW in the medium V r is:

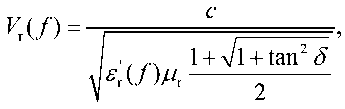
where exW ^

„           2л f 5₀ .

tan 5 =-----_;---—-:

^r(/)

μ r – magnetic permeability the medium; tgδ – the tangent the dielectric loss angle; σ dc – the final conductivity direct current losses in the dielectric; ε 0 = 8,854187817×10^–12 F/m – the permittivity the vacuum.

Unlike materials with noticeable magnetic properties such as iron (ferrites), cobalt, nickel and their alloys, many materials are not magnetic, which makes their magnetic permeability very close to that vacuum μ _r ≈ 1 (air, water, aluminum, copper), therefore, in such oil-absorbing dielectric medium as snow, firn and ice, the dielectric losses at frequencies of 2…8 GHz are small [4, 7], and the speed EW propagation in the medium V _r depends only on the relative permittivity ε^′ _r medium. In frequency bands f = 2…8 GHz the imaginary part ε ^ʺ( f ) small compared to the real part ε ^ʹ ( f ) and do not show a relaxation of the permittivity. Under these conditions, the EW propagation rate is determined for nonsaline medium

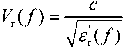
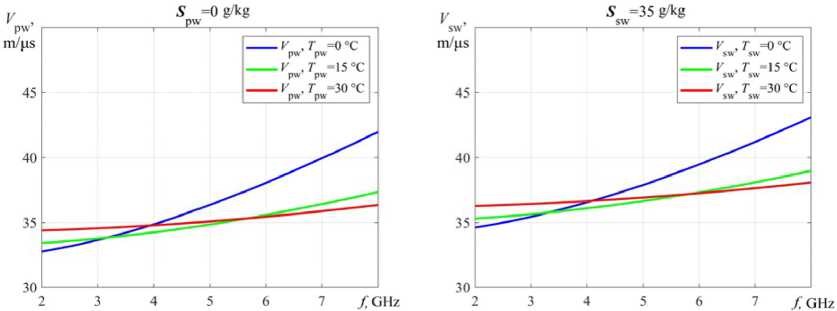
Complex relative permittivity ε _pw pure water S _pw = 0 g/kg (Fig. 4а), ε _sw sea water S _sw = 35 g/kg (Fig. 4b) and the speed propagation EW in pure water V pw S pw = 0 g/kg (Fig. 5а), V sw sea water

а)                                                                 b)

Fig. 4. Dependence the complex relative permittivity: a – ε pw pure water S pw = 0 g/kg by (1-3); b – ε sw sea water S sw = 35 g/kg by (4-6) from frequency f = 2…8 GHz at T r = 0; 15; 30 °C

а)                                                                 b)

Fig. 5. Dependence the EW propagation rate for: a – V pw pure water S pw = 0 g/kg by (2) and (13); b – V sw sea water S sw = 35 g/kg by (5) and (13) from frequency f = 2…8 GHz at T r = 0; 15; 30 °C

S sw = 35 g/kg (Fig. 5b) in the operating frequency range f = 2…8 GHz it has a smoothly changing character.

With increasing temperature T r = 0; 15; 30 °C and frequency f the changes are more pronounced.

The real part the complex relative permittivity dry ice ε^′ di does not depend on frequency f = 2…8 GHz (Fig. 6а), but only from the temperature T di = 0; –10; –40 °C within a small range, which is also seen on the velocity propagation EW V di (Fig 6b).

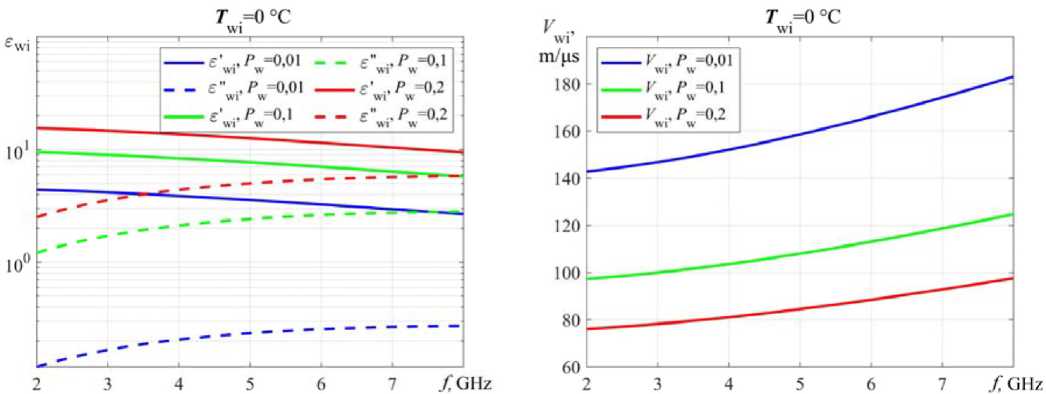
Significant contribution to the complex relative permittivity wet ice ε wi contributes a percentage water content P w (Fig. 7). For the frequency f = 2; 8 GHz by T wi = 0 °C there is a very strong growth both real and imaginary parts.

With increasing frequency f = 2…8 GHz there is a decrease in the actual part the complex relative permittivity wet ice ε^′ wi (Fid. 8а) and accordingly the increase in the speed EW propagation in wet ice V wi (Fig. 8b), with a fraction the water content P w = 0,01; 0,1; 0,2.

10°

10"*

IO"2

IO"-

-----е di, 7^=0 °C

di' di di, rdi-20 ”C 'd., ^--20 °C di" 7di“'40 °C

' , Г =-40 °C

10"* u 2

/GHz

b)

а)

Fig. 6. Dependence: a – the complex relative permittivity dry ice ε di by (7-9); b – propagation rate the EW V di by (8) and (13) from frequency f = 2…8 GHz at T di = 0; –10; –40 °C

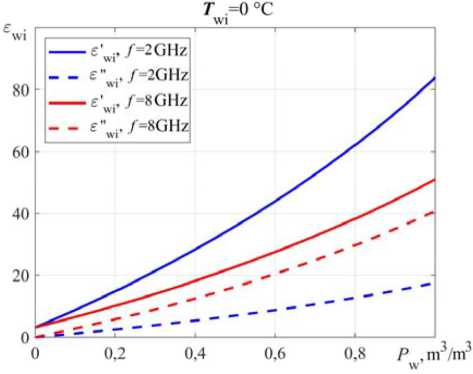
Fig. 7. Dependence the complex relative permittivity wet ice ε wi by (10) from the proportion of content liquid water P w for the f = 2; 8 GHz at T wi = 0 °C

а)

b)

Fig. 8. Dependence: a – the complex relative permittivity wet ice ε wi by (10); b – propagation rate the EW in the wet ice V _wi by (10) and (13), with the proportion of the liquid water content P _w = 0,01; 0,1; 0,2 from the frequency f = 2…8 GHz at T wi = 0 °C

Snow cover both on land and on glaciers, depending on the conditions formation and occurrence, is in a dry or wet state, it consists layers and layers snow and ice different densities, water content and structures formed as a result snowfalls, thaws and cold spells.

Depending on the proportion water content, the snow cover is a two-phase (dry) or three-phase (wet) system consisting ice crystals, water and air containing water vapor.

To describe the relative permittivity snow ε^′ s as a mixture two dielectrics ice and air with relative permittivity ε^′ i and ε^′ a or ice and water with relative permittivity ε^′ i and ε^′ w as a function their volume concentration a number equations are proposed in the works [2, 14-18].

In the first approximation, the dependence the dielectric constant the medium ε^′ r (dry snow ε^′ ds , firn ε^′ df , ice’s ε^′ di ) from density ρ r ( ρ ds , ρ df , ρ di ) and volume content the medium v r ( v ds , v df , v di ) can be described by K. Lichtenecker’s formula [2, 20]:

lg ε^′ r = v r lg ε^′ i (1 – v r ) lg ε^′ a(w) ,                                                                (14)

where v r = ρ r / ρ i – volume content medium; ρ i = 917 kg/m³ – the density dry ice without air inclusions.

Lueng’s formula [2, 21, 22] for such medium with spherical air and ice inclusions:

^=^(V?-i)+i),                                           (15)

where v i = ρ r / ρ i – volume content ice; ρ r – density the dry medium (dry snow ρ ds , firn’s ρ df , ice’s ρ di ).

According to the empirical formula of G. Robin [2, 21], the dielectric constant of the medium is determined by

ε^′ r = (1 + 8,845 ρ r )⁴.                                                                   (16)

Close ratio [2, 24]

ε^′ r = (1 + 0,848 ρ r )²,                                                                   (17)

obtained from the analysis radar logging a borehole on the Island Devon (Canadian Arctic Archipelago) and in the analysis of radiosonde data on the McMurdo ice shelf (Antarctica) and available laboratory and field measurement materials [2, 25]

ε^′ r = (1 + 0,845 ρ r )². (18)

Experimental dependencies obtained by different authors ε^′ r ( ε^′ ds , ε^′ df , ε^′ di ) from density ρ r ( ρ ds , ρ df , ρ di ), they show a very close agreement with the calculations based on the G. Lueng formula (15), while the maximum discrepancy with the results calculations based on empirical and computational dependencies does not exceed 2…3 % by ε^′ r ( ε^′ ds , ε^′ df , ε^′ di ) at a density more than 400 kg/m³ [2]. The real part the complex relative permittivity the medium ε^′ r (snow, firn, ice) and the speed EW propagation in the medium V r with density ρ r – 100; 500; 700; 917 kg/m³ according to (15) do not depend on f = 2…8 GHz, but only from T within small limits as for dry ice (Fig. 6). Relative permittivity a wet medium ε^′ vr (wet snow ε^′ ws , firn’s ε^′ wf , ice’s ε^′ wi ) depending on the percentage water content P w it is also described by the Lueng formula [2, 22]. For a two-component ice-water mixture with water-filled pores

<=(^>f.(v<-^)) ,(19)

where ε^′ i and ε^′ w relative permittivity ice and water, respectively.

For a three-component medium consisting ice with water and air inclusions, given (22) we obtain [2, 26]

( I                      / /—"—\ \ 3

^ = ^'Л'-р^+р.             ,(20)

where P wa – the total percentage water and air content («total» porosity warm ice).

Relationship between the relative permittivity a dry medium ε^′ r and humid medium ε^′ vr can be described by formulas [2, 24]:

ε′r = (1 + 1,7 ρr + 0,80 ρr2);(21)

ε′vr = (0,1Pw + 0,80 Pw2) ε′w + ε′r;(22)

εʺvr = (0,1Pw + 0,80 Pw2) εʺw,(23)

where ε^ʺ vr and ε^ʺ w – factors wet environment and water loss, respectively.

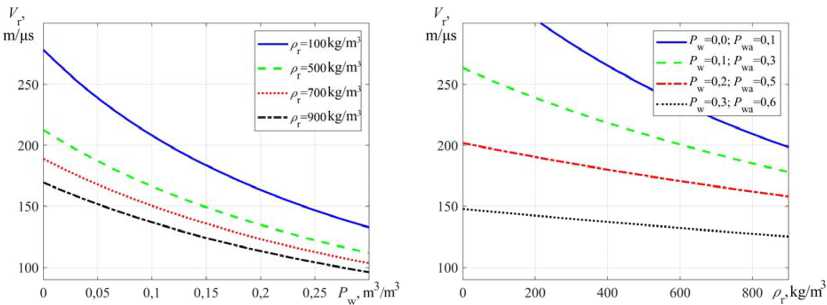
With an increase in the proportion water content in the medium P w (Fig. 9а) there is a drop in the speed EW propagation in the medium V r (snow, firn, ice) with completely filled pores with water calculated by (19) and the density the medium ρ r (Fig. 9b), there is also a drop in the rate EW propagation in the medium V r with a total share water and air P wa – 0,1; 0,3; 0,5; 0,6 and water P w – 0; 0,1; 0,2; 0,3 according to (20) for f = 8 GHz by T r = 0 °C, a with an increase in the proportion air content P а speed increases.

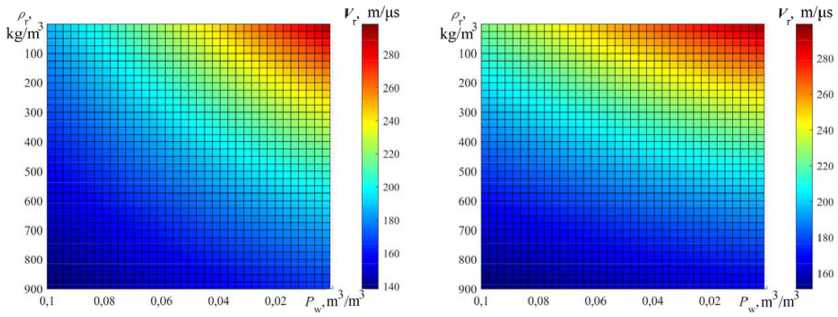
The speed of propagation EW in the medium V r (right scale) depending on the percentage water content P w = 0…0,1 (lower scale) and medium density (snow, firn, ice) ρ r (left-hand scale) at T r = 0 °C for the frequency f = 2 GHz (Fig. 10а) and f = 8 GHz (Fig. 10b) shows an increase in speeds on compared to in looser structures and a drop in denser structures.

b)

а)

Fig. 9. Dependence propagation rate the EW by V r (snow, firn, ice) from a – percentage of liquid water content P w for medium density ρ r – 100; 500; 700; 900 kg/m³ with fully filled pores with water by (19); b – density of medium ρ r with a total proportion of liquid water and air P wa – 0,1; 0,3; 0,5; 0,6 and liquid water P w – 0; 0,1; 0,2; 0,3 by (20) for f = 8 GHz at T r = 0 °C

а)

b)

Fig. 10. Dependence propagation rate the EW by (snow, firn, ice) (13) V r (snow, firn, ice) from the density of the medium (21) ρ r and the percentage of liquid water content (22) P w = 0…0,1 for: a – f = 2 GHz; b – f = 8 GHz at T r = 0 °C

How can it be seen that for dry medium, the EW propagation velocity at T r = 0 °C are in the intervals: for dry snow – V _ds = 278,1…212,7 m/μs; for dry firn – V _df = 212,7…189,0 m/μs; for dry ice – V di = 189,0…167,9 m/μs. The picture is changing with the increase in the proportion water content P w , because for pure water V pw = 32,74…41,97 m/μs.

An important factor affecting the speed EW propagation is the shape, size, and orientation air and water inclusions in dry and wet snow, firn, and ice. In [28] it is shown that when water inclusions are perpendicular to the EW direction, they have high velocities in the ice, and lower velocities when they are parallel to the EW direction, i.e. if the inclusions are drawn parallel and normal to the ice surface the snow-ice cover.

For medium with disc-shaped inclusions, the dielectric constant in the parallel direction £ || and perpendicular £ EF, described by the ratio [2, 28]:

= U£^Jf1fw4'4a+£^^

;

E 32^^25^1^551^^

C' (l + 2/4d) + f 0-P ) + (2-2Ла)£ .   , where εi and εw the permittivity the host ice and water inclusions, respectively; Pw – volume fraction water content; Ad – depolarization factor that characterizes how ordered the orientation inclusions is (stretched in one direction – Ad = 1, randomly placed – Ad = 0).

The calculations performed by Kotlyakov V.M., Macheret Yu.Ya., Sosnovsky A.V., Glazovsky A.F. in [2] indicate the applicability the Lueng formula (19) for estimating the average density dry snow cover and show that the speed EW propagation in snow, firn, and ice depends on the density ρ _r, the proportion water content P _w, the structure can change over a wide range. So in dry snow cover, with an average density of ρ ds = 400…500 kg/m³, the average speed is close to the EW V _ds = 190 m/μs. However, it will change greatly depending on the preferred orientation and shape ice and air inclusions in the snow. In dry snow with vertically and horizontally elongated and spherical inclusions the speeds differ by 38 m/μs (16 %) at a snow density of 300 kg/m³ and at 15 m/μs (7 %) at a density of 500 kg/m³ and the ratio semi-axes ellipsoids p = 2. By p = 4 this difference is 61 m/μs (26 %) and 23 m/μs (11 %) respectively.

Conclusion

Thus, if it is possible to remotely measure the speed EW propagation in medium V r , the average density medium ρ _{r aver} can be estimated, as well as the average water content in medium P _{w aver}, which will allow remote identification the medium (underlying surface), more accurately determine the depth snow and the thickness the ice cover, in order to perform a safe landing a helicopter-type aircraft on an unprepared area with snow and ice cover.

When the proportion water content in the medium P _w = 0, for the temperature the medium T r < 0 °C, which is typical, for example, for the Arctic territories, the task identifying the medium (underlying surface) is simplified, since the speed EW propagation in the medium V _r will depend only on the density ρ r and the structure these medium.

Knowing the intervals electromagnetic wave propagation speeds V _ds = 278,1…212,7 m/μs for dry snow, V df = 212,7…189,0 m/μs for dry firn and V di = 189,0…167,9 m/μs for dry ice, allows you to remotely identify the medium and more accurately determine the depth snow and the thickness the ice cover to assess the possibility landing a helicopter-type aircraft on an unprepared area with snow and ice cover.