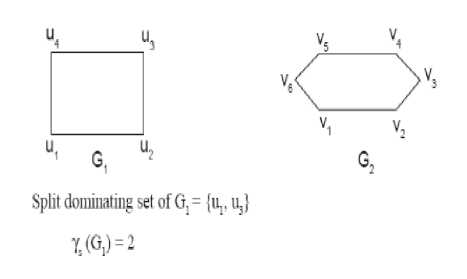
The Split Domination in Product Graphs

Published Online October 2013 in MECS

• I.    INTRODUCTION

  Graph theory is one of the most flourishing branches of modern mathematics. The last 30 years have witnessed spectacular growth of Graph theory due to its wide applications to discrete optimization problems, combinatorial problems and classical algebraic problems. It has a very wide range of applications in many fields like engineering, physical, social and biological sciences, linguistics etc., The theory of domination has been the nucleus of research activity in graph theory in recent times. This is largely due to a variety of new parameters, that can be developed from the basic definition of domination. The NP-completeness of the basic domination problems and its close relationship to other NP-completeness problems have contributed to the enormous growth of research activity in domination theory. It is clearly established from the exclusive coverage of the “Topics on domination in graph” in the 86^th issue of the Journal of Discrete mathematics (1990), that the theory of domination is a very popular area of research activity in graph theory. Most of the terminology of the paper considered from references ^[1] [3] .

The rigorous study of dominating sets in graph theory began around 1960, even though the subject has historical roots dating back to 1862 when the Jaenisch studied the problems of determining the minimum number of queens which are necessary to cover or dominate a n x n chessboard. In 1958, Berge defined the concept of the domination number of a graph, calling this as “coefficient of External Stability”. In 1962, Ore used the name ‘dominating set’ and ‘domination number’ for the same concept. In 1977 Cockayne and Hedetniemi made an interesting and extensive survey of the results know at that time about dominating sets in graphs. They have used the notation γ (G) for the domination number of a graph, which has become very popular since then.

The survey paper of Cockayane and Hedetniemi has generated lots of interest in the study of domination in graphs. In a span of about twenty years after the survey, more than 1,200 research papers have been published on this topic, and the number of papers continued to be on the increase. Since then a number of graph theorists Konig, Ore, Bauer, Harary, Lasker, Berge, Cockayne, Hedetniemi , Alavi, Allan, Chartrand, Kulli, Sampthkumar, Walikar, Armugam, Acharya, Neeralgi, Nagaraja Rao, Vangipuram many others have done very interesting and significant work in the domination numbers and the other related topics [5] [6]. A recent book on domination [2], has stimulated sufficient inspiration leading to the expansive growth of this field of study. It has also put some order into this huge collection of research papers, and organized the study of dominating sets in graphs into meaningful sub areas, placing the study of dominating sets in even broader mathematical and algorithmic contexts.

Motivated by the study of domination and split domination we have investigated some properties of a split domination number of the product graphs.

Important definitions:

• 1.1:    Dominating set:

A subset D of V is said to be a dominating set of G if every vertex in V \ D is adjacent to a vertex in D.

• 1.2:    Dominating number:

The dominating number γ (G) of G is the minimum cardinality of a dominating set.

• 1.3:    Split dominating set:

A dominating set D of a graph G is called a split dominating set, if the induced subgraph is disconnected.

• 1.4:    Split domination number:

The split dominating number γ s (G) of G is the minimum cardinality of the split dominating set.

• 1.5:    Kronecker Product of two graphs

If G1, G2 are two simple graphs with their vertex sets V1: {u1, u2,…..} and V2: {v1, v2, …..} respectively, then the Kronecker product of these two graphs is defined to be a graph with its vertex set as V1 x V2, where V1 x V2 is the Cartesian product of the sets V1 and V2 and two vertices (ui, vj), (uk, vl) are adjacent if and only if ui uk and vjvl are edges in G1 and G2 respectively.

This product graph is denoted by G1 (k) G2.

• 1.6:    Cartesian product of two graphs

If G1, G2 are two simple graphs with their vertex sets V1: {u1, u2,…..} and V2: {v1, v2, …..} respectively, then the Cartesian product of these two graphs is defined to be a graph with its vertex set as V1 x V2 : {w1, w2, …..} and two vertices w1 = (u1, v1) and w2 = (u2,v2) are adjacent if and only if either (i) u1 = u2 and v1v2 ε E (G2) or (ii) u 1u2 ε E (G1) and v1=v2.

This product graph is denoted by G1 (C) G2.

• 1.7:    Lexicograph product of two graphs

If G1, G2 one two simple graphs with their vertex sets V1: {u1, u2,…..} and V2 : {v1, v2, …..} respectively, then the Lexicograph product of these two graphs is defined to be a graph with its vertex set as V1 x V2: {w1, w2, …..} and two vertices w1 = (u1, v1) and w2 = (u2,v2) are adjacent if and only if either (i) u1 u2 ε E(G1) or (ii) u1 = u2 and v1v2 ε E (G2).

This product graph is denoted by G1 (L) G2.

In this paper ,we have obtained several interesting results on split domination of some product graphs.The organization of the paper is as follows: Section II describes several interesting relationships of γ s(G) with the other known parameters. Some results on Split dominating sets and Split domination numbers of certain types of Product Graphs are discussed in Section III and finally the conclusion of the paper is given in Section IV.

• II.  SOME RESULTS ON SPLIT DOMINATION OF

STANDARD GRAPHS

• i.     γ _s (G) ≤ α _o (G), where α _o (G) is a vertex covering

number

• ii.    γ (G) ≤ γ s(G)

• iii.    k (G) ≤ γ s(G)

• iv.    γ s(G) ≤ P. ∆ (G) , where ∆ (G) is the maximum degree of G. ∆ (G)+1

• v.    γ s (G) ≤ δ (G); If Diam (G) = 2, where δ (G) is the

minimum degree of G.

• vi.  They have obtained the split domination number of

some standard graphs as follows:

• vii.    γ S (CP) = [ p/3], where [x] is the lease + ve integer not less than x and CP is a cycle with p ≥ 4 vertices

viii. (vii) γ s (WP) = 3 , Where WP is a wheel with p ≥ 5 vertices

• ix.  (Viii) γ s (Km, n) = m, Where 2 ≤ m ≤ n and Km, n

is a complete bipartite graph.

Weichsel [10] has proved that if G1, G2 are connected graphs, then G1 (k) G2 is connected if and only if either G1 (or) G2 contains an odd cycle. It was further proved that if G1 , G2 are connected graphs with no odd cycle, then G1 (k) G2 is a disconnected graph. Sampath Kumar [7] has proved that if G is a connected graph with no odd cycles, then G (k) K2 = 2 G.

It can be easily seen that;

deg G₁ (k) G₂ (u i , v j ) = deg G₁ (u i ) . deg G₂ (v j )

We recall some of the results on these product graphs.

• Theorem 2.1:

In G1 (k) G2 , deg (ui, vj) = deg (ui) . deg (vj)

• Theorem 2.2:

If G1, G2 are finite graphs without isolated vertices, then G1 (k) G2 is a finite graph without isolated vertices.

• Theorem 2.3:

If G1, G2 are regular graphs,then G1(k) G2 is also a regular graph.

• Theorem 2.4:

IfG1 ,G2 are bipartite graphs,then G1(k) G2 is a bipartite graph.

Remark 2.5:

However, it is to be noted that If G1, G2 are simple graphs, then G1(k)G2 can never be a complete graph, for (ui, vj) is not adjacent with (ui, vk) for any j ≠ k (By definition 1.5)

We have obtained the following results.

• III.    SPLIT DOMINATION OF PRODUCT GRAPHS

In this section, we have obtained some results on Split dominating sets and Split domination numbers of certain types of Product Graphs.

• Theorem 3.1:

If G1 is any graph on p-vertices and Sn is a star on n-vertices.

Then γ s (G 1 (k)S n ) = p = | V (G 1 )|

Proof : Let V (G 1 ) ={ u 1 , u 2 , …………… u p } and

• V (S n ) = {{v 1 , v 2 , ……………. v n }

Let    D s (G 1 ) ={ u 1 , u 2 , …………… u p } and

D s (S n ) = {v 1 }, where v 1 is the only vertex in S n whose degree is >1.

Now the set D s (G 1 ) x D s (S n ) is a vertex cut of

G ₁ (k) S _n as illustrated in Fig 1.

However this set is not a dominating set.

It can be easily seen that the set of vertices

D = {(u1, v1), (u2, v1) ……………. (up, v1) } is a dominating set.

Further this is also a split dominating set.

For, the vertex of the form (ui, vj), for j ≠ 1 is not adjacent with any vertex in .

Now D is a split dominating set of minimum cardinality.

Suppose, if we delete a vertex ( ui, v1) from the set D, then this vertex (ui,v1) is not adjacent to any vertex in the set Ds(G1) x Ds(Sn). Thus D is not a dominating set and hence not a split dominating set.

Hence this is a split dominating set of minimum cardinality.

Therefore γ s (G (k) S n ) = p = | V(G 1 )|

Illustration:

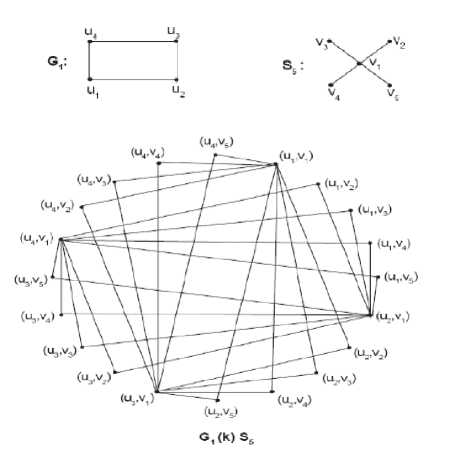
Figure 1: Graph of G 1 (k)S 6

Here D = {(ui,vi), (u2,vi), (u3,vi), (гад)}

The removal ofD vertices from Gi(k)S; will make the induced sub graph disconnected.

Thus D is a split dominating set. The cardinality of this set is 4.

HenceTs[G1(k)SB] = 4=|V(Gi)|

We have also obtained the following result regarding the split domination of the Kronecker product graph G1(k)G2, where G1, G2 are any two graphs.

• Theorem 3.2:

If G1, G2 are any two graphs, then γ s[G1(k)G2] ≤ min [ γ s(G1).|V2|, |V1|. γ s (G2)]

Proof : Let G 1 be a graph with p vertices with

V(G1) = { u1, u2, ………uP1} = V1say and G2 is a graph with p2 vertices with

V(G 2 ) = { v 1 , v 2 , ………v P₂ } = V 2 say

Let D 1 = { u d₁ , u d₂ ,……….. u d_r },

D2 = { vd1, vd2,……….. vds} be the split dominating sets of minimum cardinality of G1, G2 respectively.

The removal of the D1 vertices in G1 will make the induced sub graph < V1 – D1> to be disconnected graph.

Consider the set of vertices

D s = { (u d₁ ,v 1 ), (u d₁ ,v 2 )……….. (u d_1, v P₂ ),

(u d₂ ,v 1 ), (u d₂ ,v 2 )……….. (u d_{2 ,} v P₂ ) ,

(u d_r ,v 1 ), (u d_r ,v 2 )……….. (u d_{r ,} v P₂ ) }.

This is dominating set of G1 (k) G2 as shown in Fig 2.

For, if (u, v) is any vertex of in G1 (k) G2, u is adjacent with at least one vertex in { ud1, ud2,……….. udr}, as this is the dominating set of G1 being its split dominating set.

Now suppose v is adjacent with some vertex vk in G2 (certainly there exits at least one vertex vk in G2, since G2 has no isolated vertices).

Thus (u, v) is adjacent with (udi, vk) in Ds.

Therefore Ds is a dominating set.

Further this is also a split dominating set.

It can be established as follows:

We know that D1 is a split dominating set of G1. The induced sub graph is disconnected graph.

Let ui, uj be any two vertices in two different components of

Thus Ds is a split dominating set of G1 (k) G2 as illustrated in Fig 3.

Similarly, by the same argument we can prove that

The set Ds ′ = { (u1, vd1), (u2, vd1)…….. (up1, vd1), (u1, vd2) (u2, vd2),……. (up1, vd2), (u1, vds) (u2, vds),…… (up1, vds)}is also a split dominating set of G1 (k) G2 as illustrated in Fig 4 .

Hence γ s [G1(k)G2] ≤ min [ |Ds|, |Ds ′ |]

Thus γ s [G1(k)G2] ≤ min [ γ s(G1).|V2|, |V1| . γ s (G2)]

Illustration:

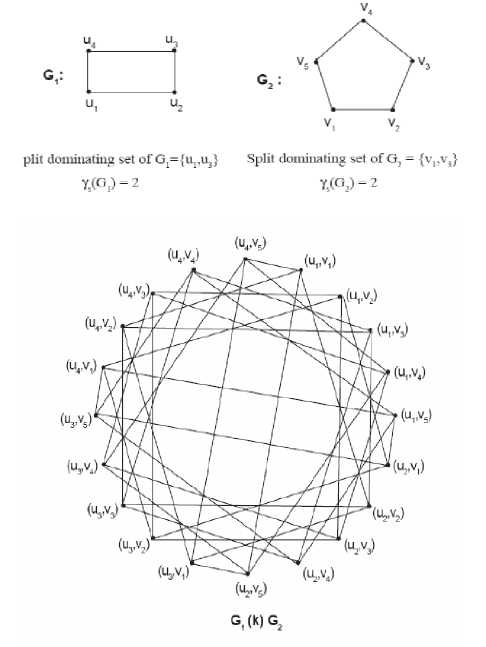
Figure 2: Graph of G 1 (k)G 2

The split dominating set

D,= {^Ujlx^YpVj.V^V,}

= l(ur Vj, (l^,V2), (Upvj. (UpV^ (Urvs). (11^), (yj, (UpVj), (“y^: (11^)}

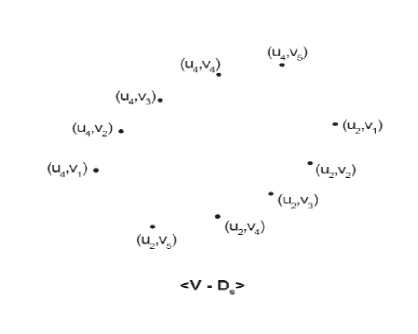
Figure 3: Graph of < V{G 1 (k)G 2 }-D s >

is disconnected

that is |DJ = у (Gt). V(G.) = 2.5 = 10

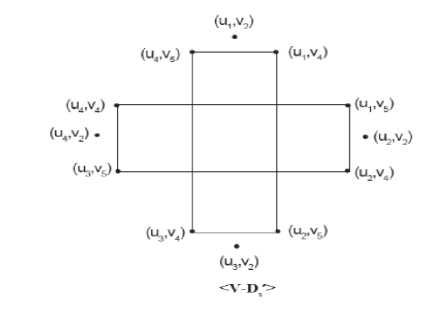
Figure 4: Graph of < V{G 1 (k)G 2 }-D s ' >

Thus D/ is another split dominating set.

|D'|-|V,| .Y,(O2)-4.2-8

X[G,(k)GJ< mm[|DJ,|D/|]

• - min [y, (G^ . I V₂1, | V, | . y, (G₂) ] = min [10. 8]

  - 8

Therefore Y. [Gt (k) G3] < 8

We recall some of the results already established by Sampath Kumar [7] for the Cartesian Product Graph.

• Theorem 3.3:

If G1, G2 are bipartite graphs, then G1 (C) G2 is also a bipartite graph.

• Theorem 3.4:

If G1, G2 are simple finite graphs without isolated vertices, then G1(C) G2 is also a simple finite graph without isolated vertices.

Now we obtain a relationship between the split dominating number of G1(C)G2 and the split dominating numbers of G1 and G2.

We obtain the following result.

• Theorem 3.5:

If G1, G2 are any two graphs without isolated vertices, then γ s [G1(C)G2] ≤ γ s(G1). |V2|

Proof : Let G 1 be a graph with p vertices with

V (G1) = { u1, u2…………..up} = V1 say

And G2 be a graph with q vertices with

V(G2) = {v1, v2, ……….vq} = V2 say

Let D1 = {ud1, ud2,………….. udr} be the split dominating set of G1 of minimum cardinality.

This means that the induced sub graph of G1 is a disconnected graph.

Let D2 = {vd1, vd2, ……….vds} be a split dominating set of G2 of minimum cardinality.

The induced sub graph is a disconnected graph.

Now consider the set of vertices

Ds={ (u d₁ , v 1 ), (u d₁ , v 1 ), ……….…,( u d_r , v 1 ),

(u d₁ ,v 2 ), (u d₂ ,v 2 ), …..……….,(u d_r , v 2 ),

(u d₁ ,v q ), (u d₂ , v q ), ………….,(u d_r , v q )}

G, (О G,

Figure 5: Graph of G 1 (C)G 2

This is a dominating set of G1 (C) G2 as illustrated in Fig 5.

For, if (u, v) is any vertex of in G1 (C) G2,v will be adjacent with at least one vertex in D2, which is the split dominating set of G2 say vdi ,then (u, v) is adjacent to a vertex (u, vdi) in D.

Hence Ds is a dominating set of G1(C)G2 as illustrated in Fig.6.

Let vi, vj be two vertices in in two different components.

Then it follows that (u, vi) and (u, vj) are in two different components of an induced sub graph

s > of G 1 (C)G 2 .

Thus D _s is a split dominating set.

Hence         γs [G1(C)G2] ≤ |Ds| and so γs [G1(C)G2] ≤ γs (G1).|V2|

Illustation:

Ц = {uru3}x{vrv,,v3,v4,v3,vj

= {(^.V,), (UpV,), (UpVj), (UpV^ (UpV^. (upv6), (u^v,), (u,^ (^V,), (^V,), (и^Д (g,^}

Figure 6: Graph of < V{G 1 (C)G 2 }-D s >

D3 is a split dominating set.

ID | = y5 (G,) . |V2| = 2.6 = 12

TJG^OGJ^ |D I-12

Y_s[G,(C)G₂] <  12.

It has already been established by Sampath Kumar [7] that

• Theorem 3.6:

If G1, G2 are simple finite graphs without isolated vertices, then G1(L)G2 is a finite graph without isolated vertices.

Now we obtain an expression for the split domination number of G1(L) G2 in terms of the split domination numbers of G1, G2.

• Theorem 3.7:

If G1, G2 are any two graphs without isolated vertices, then γ s [ G1 (L) G2] ≤ γ s (G1) . |V2|

Proof: Let G 1 be a graph with p vertices with

V(G1) = {u1, u2, …uP} = V1 say and G2 be a graph with q vertices with

V (G 2 ) = {v 1 , v 2 , …. v q } = V 2 say

Let D 1 = {u d₁ , u d₂ ……..u d_r } and

D2 = {vd1, vd2, ……..vds} be the split domination sets of minimum cardinality of G1, G2 respectively.

Consider the set

D s = { (u d₁ , v 1 ), (u d₁ , v 2 ), ……….…,( u d₁ ,v q ),

(u d₂ ,v 1 ), (u d₂ ,v 2 ), …..……….,(u d₂ ,v q ),

(u d_r ,v 1 ), (u d_r ,v 2 ), ………….,(u d_r ,v q )}

This is the dominating set of G1(L) G2 as shown in

Fig. 7.

For, if (u, v) is any vertex in , then we have the following two cases :

Either u is in D1 or u is in < V1 – D1>.

If u is in D1, then u = udi for some i. The vertex

(u, v) = (udi, v) and v will be adjacent to some vertex in D2 = {vd1, vd2, ………… vds}.

For the sake of definiteness, suppose v is adjacent with vdj for some j, then (u, v) = (udi, v) is adjacent with (udi, vdj)

Thus Ds is a dominating set.

Suppose ui, uj be two vertices in two different components of the induced subgraph of G1.

Then it follows from the definition of the split domination 1.3 and from the definition of the Lexicograph product graph 1.7, the vertices (ui, v) ,

(uj, v) will be in two different components of of G1 (L) G2.

Thus Ds is a split dominating set of G1 (L) G2as illustrated in Fig. 8.

Hence γs [G1(L) G2] ≤ |Ds| and so γs [G1(L) G2] ≤ γs (G1) . |V2|

Illustration:

Figure 7: Graph of G 1 (L) G 2

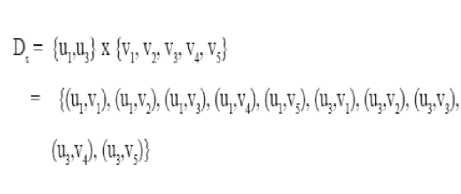
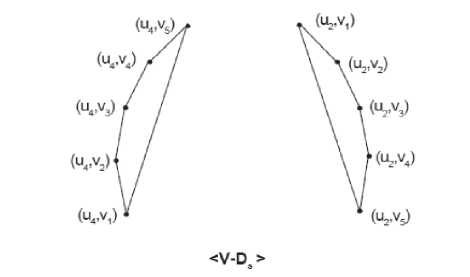
Figure 8: Graph of < V{G 1 (L)G 2 }-D s >

Da is a split dominating set, |DJ=Ts(G1).rV2| = 2.5=10 X^^GJS |DJ =10 Ш(Ц0,]< 10

• IV. CONCLUSION

The tools of Graph theory enable us to develop a simple method of constructing a graph with a given cardinality of the spilt dominating set with amazing ease. It is also amazing to observe how such a graph with a given domination number can be enlarged to include more vertices and edges in a methodical, simple manner without affecting the domination number. We can apply this to many applications such as to eradicate pests in

Agriculture, to control viruses which produces diseases in an epidemic form, to maintain confidential in transferring the information, especially very useful for Defense sector. To some extent this may be due to the ever growing importance of computer science and its connection with graph theory.