The Stability of Memory Rules Associative with the Mathematical Thinking Core

Published Online February 2011 in MECS

Memory stability, the ability to retain the past information and to influence future results [1], is thought to be due to the persistence of memory information, but remains flexible in face of environmental perturbations [2]. In an educated human, experiential knowledge could provide the foundation for an integration with stability-based processing of numbers. Much of advanced mathematics is built on basic number-processing skills, which is thought to be supported by a distributed network of various brain regions, including fronto-parietal (for a review, e.g., [3]) and other areas associated with various tasks [4]. A wealth of neuroimaging data [5-7] has revealed that activity in the fronto-parietal areas correlates with task rules in number-processing, which was measured either by retrieving a pure arithmetic fact or by calculating a memorized multi-fact task [8]. Therefore, core systems may serve to process concepts or facts, independently of non-numerical or numerical symbols. Nevertheless, the basic ability to calculate numerical tasks cannot fully explain the extent of human mathematical skills. During learning of advanced mathematics, a large set of unique human skills emerge, which provide a person with the ability to understand abstract mathematical rules (such as Boolean rules and integral calculus) and perform mathematical operations based on core systems of number.

The present study had two objectives – namely to 1) determine cortical activation during retrieval of Boolean rules associated with number-processing cognition, and 2) to locate the core systems of stabilized memory within the brain, in particular, which regions of the brain exhibited evidence of the process sources of mathematical thinking. The answers to these questions will provide a greater understanding for the relationship between stable mathematical memory and background knowledge. One particular challenge is how to distinguish between stable memory and memories resulting from memory-related effects. Exact small-number calculations in adult number-processing systems, for example, are processed differently from number-based calculations, a process which allows for immediate and accurate retrieval. Stability has been proposed to depend on systems that represent and track small-number processing [9, 10]. Exact small-number arithmetic (arithmetic facts) relies on visuospatial representation and linguistic competence [6, 11]. Arithmetic facts with stability, such as multiplication tables, use linguistic representation, which has been associated with memory and sequence execution [12]. Moreover, multiplication problems could be solved by retrieving the rule strategy from long-term memory, like decomposing a problem into smaller facts in counting [13]. To overcome the complexities of studying stable memory, Boolean rules were used, which differed only in the signs expressed. These stimuli are advantageous, because they retrieve memory strategies along a single dimension.

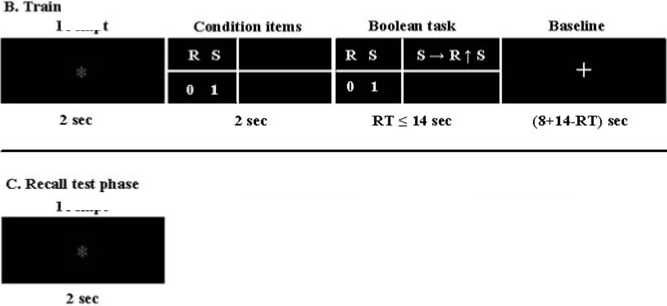
In the present study, according to Ebbinghaus’ memory paradigm [14] and the theory of working memory capacity[15], the effects of memory stability of Boolean rules based on background knowledge, as well as the relationship between Boolean rules and core systems of number-processing, were investigated. Specifically, the possibility of estimating the same regions of brain activation patterns for core mathematical thinking was analyzed. For each problem of the seven kinds of rules in Table 1[16], a set of problems, such as P↑Q→P were presented during a 1-week training period (Fig. 1B). Training success was measured in decreasing reaction times and error rates. The first two kinds of rules in Table 1 served as background knowledge. In a subsequent fMRI session (day 7), trial retrieval consisted of the last five kinds of rules (every kind of rule contains 4 expressions) in Table 1 (Fig. 1C). Two hypotheses are possible. First, it was assumed that the time-dependent learning utility had crucial influence, and simultaneously, that extensive and repetitive training for the rules in Table 1 should lead to similar modifications of brain activation. Second, it was assumed that characteristics inherent to the last five kinds of rules in Table 1 determine the acquisition process extensive and repetitive training should be based on number-processing and lead to an identical core of activation patterns. Based on previous studies [9, 10], these predictions could be applied to Boolean rules. Trained rules exhibited identical activation in the left parietal and left inferior frontal regions, and serve to process the simple arithmetic operations (arithmetical facts), while the trained rules exhibited a significant focus of activation around the fronto-parietal region [12]. These experimental effects have not been previously shown. The present study summarized the experimental analysis of behavior analysis and then reported the fMRI results for the stability of Boolean rules association with the core systems of number-processing.

TABLE I. Boolean rules

C1	C2	AND	OR	IMP	EQU	NAND	NOR	XOR
P	Q	P∧Q	P∨Q	P→Q	P←→Q	P↑Q	P↓Q	P▽Q
0	0	0	0	1	1	1	1	0
0	1	0	1	1	0	1	0	1
1	0	0	1	0	0	1	0	1
1	1	1	1	1	1	0	0	0

A. Experimental scheme Codeless

Encoding (Labile)

(Re)consolidation

Stabilized

Before day 1

Day 1

Day 2/3/4/5/6

Day 7

Untraining

Learning 2h Practice 20 trials/times untill accuracy; 80%

Practice 20 trials/times untill accuracy > 80%

Practice 20 trials/times untill accuracy > 80% fMRI (Long-test)

Session 1 x 40 trials

fMRI (Pre-test) Session 1 x 40 trials fMRI (Post-test) Session 1 x 40 trials ting scheme Prompt

(In)correct

Response time Average percent correct

Feedback

Prompt

(8+6-RT) sec

-^- time

Fig. 1. The experimental set-up. (A) Experimental scheme. (B) Training scheme. (C) Recall test phase.

• II.    Experimental Procedures

• A.    Participants

• 23.2±2.5 years) participated in the study. All participants

Eighteen university students (9 females; mean age

were informed about the procedure and gave written consent to participate in the experiment. The study was approved by the Ethical Commission of the Xuanwu Hospital of Capital Medical University. Six subjects had to be discarded from the analysis due to technical problems with the unsuccessful data collection (n=5) or excessive motion of the head (n=1). Thus, fMRI image analysis is based on the data from 12 participants [16].

• B.    References Training procedure

To examine the stable processes underlying learning-dependent memory, Boolean arithmetic tasks were utilized, with two operator symbols that served as trained tasks (Fig. 1B). fMRI test tasks were similar to those of adults’ learning artificial Boolean rules [17]. Subjects were trained on Boolean tasks until they were perfectly mastered. The subjects were tested by fMRI on the day before day 1, day 1 and day 7 (Fig. 1A). On the practice days, participants took part in seven training sessions on consecutive days and were trained on twenty Boolean arithmetic problems. Each problem comprised of two operator symbols in a set of twenty problems. The problem remained visible until the subject finished typing the solution. When the problems were presented on a computer, subjects entered the answer (1 or 0) using the number key on the computer keyboard. Reaction times were timed starting with the presentation of the problem until the answer was provided. Incorrect (correct) response times and average percent correct feedback were provided. If accuracy was < 80%, the subjects were tested on a new task set. Within a series of behavior experimental conditions, the overtime criterion was 14 s.

During the recall session, fMRI data were acquired. Subjects solved 40 Boolean problems (eight problems for each rule). Forty tasks were presented to the subject during each fMRI session. Stimuli were presented in a randomized, non-stationary, probabilistic sequence. Elements of each trial were presented in sequential order: red fixation star, conditions items of Boolean task, Boolean task, and white cross (duration of star, conditions, rule, and cross stimuli presentation was 2 s, 2 s, RT≤6 s, (8+6–RT) s, respectively)[16]. The task presentation participants were asked to retrieve the correct answer from stable memory, and press “1” or “0” on two button boxes using the right index and middle fingers (Fig. 1C). Reaction times were obtained for each trial. Subsequent to pressing the button, the next trial took place following an inter-trial interval. Stable memory tasks were assumed to primarily involve the hit retrieval of mathematic facts and template knowledge stored in long-term memory, without online calculation. Therefore, a white cross was utilized as a baseline condition.

• C.    Image acquisition and analysis

  Data acquisition. Imaging was performed on a 3.0-Tesla Siemens Scanner with a receive-only whole head coil. Prior to anatomic imaging, BOLD data were acquired by an echo-planar imaging (EPI) sequence and with AC-PC (anterior commissure-posterior commissure) on the twelfth slice from the bottom. Imaging parameters were as follows: slices=30, TR/TE=2000/31 ms, slice thickness=4 mm, slice gap=0.8 mm, flip angle=90°, FOV=256×256 mm², matrix= 64×64, 0.8×0.8×4.8mm³ spatial resolution. For each subject, the fMRI scan during run state lasted for 12 min10 s and 362 volumes were obtained. In a structural session, whole head T1 weighted images were acquired (TR/TE/TI=130/2.89/800 ms,

slices=30, flip angle=70°, matrix=320×320, slice thickness= 4mm, slice gap=0.8 mm, FOV =256×256 mm2) in the same position as the functional images.

Image preprocessing was conducted using SPM2 package ( implemented in Matlab 6.5. The first 2 volumes (10 s) of each subject were discarded to allow for magnetic saturation effects. The remaining 360 functional scans were first corrected for differences in slice acquisition time and realigned to the first volume to correct for inter-scan movements [18]. Movement parameters during spatial realignment were not greater than 3 mm and 3° for the more analysis.

Data analysis. The structural T1-weighted volumes were co registered to the mean EPI volume and spatially normalized to a standard T1 template in the space of Talairach. These normalization parameters of normalizing the structural volume were reapplied to the T2*-weighted volumes for performing spatial normalization. The functional volumes were spatially normalized to a standard EPI template. During normalization, all volumes were resampled in 3×3×3 mm3 voxels. Finally, all T2*-weighted volumes were smoothed with a 6-mm full width at half-maximum isotropic Gaussian kernel after spatial normalization.

The fMRI data were statistically analyzed using the general linear model (GLM) and statistical parametric mapping. Since the Boolean tasks were trained in a time scheme, including seven different training sessions to consolidate rule memory, practice-related changes collapsed these trials in a range of seven days as the stabilized condition. The explanatory variables (stability-based hits, trials of no interest comprising of all trials that took longer than 6 s, and intertrial intervals) were temporally convolved with the canonical hemodynamic response function (HRF) along with its temporal derivatives provided by SPM2. Regressor of the intertrial interval was used as the explicit baseline activation. Temporal filtering was achieved using autoregressive modeling (AR1) to model high-frequency noise, and a high pass filter was implemented using a cut-off period of 128 s in order to remove the low-frequency effects from the time series. These first-level results from SPM{t} contrast images were used in second-level random-effects analyses. At the second level, initially a one-sample t-test was calculated with a threshold of P < 0.05 (FWE (family-wise error)-corrected), and then the cluster-size statistics were used as the test statistic applying a threshold of P < 0.00001 (corrected, minimum cortex volume≥ 80 voxels cluster size). This analysis was limited to the brain cortex that was active for the stabilized condition. For the anatomical location of significant clusters, we transformed MNI (Montreal Neurological Institute) template Talairach space [19]. The Talairach atlas as implemented by the Talairach Daemon [20] was used as reference template for corresponding Brodmann’s Areas. Finally, we performed a region of interest (ROI) analysis in the parietal and the frontal associative cortex volume described above, in each of the task conditions compared to the average baseline.

Ш. Results

• A.    Behavioral data

Table 2 shows probabilities of correct responses and reaction time (RT) for the hit trials of pre-test (non-memory), post-test (labile memory) and long-test (stabilized memory) in three fMRI Experiments 1 , 2 and 3 (Fig. 1A). In the study phase, accuracy in detecting stability (Boolean rules) was high, with mean rates of 97.78% in long-test (the stabilized memory test) and 95.97% in post-term test (the labile memory test). Accuracy was not significant different between the long-test (stabilized) and post-test (labile).

Demands may have been relatively greater in the labile test (post-test), given that there was a greater need to encode the rules. In line with this idea, stability detection was significantly less reaction time in long-test (the stabilized memory test) than in post-test (the labile memory test) (2.35 s vs.1.66 s, respectively, t =4.22, p<0.001).

TABLE II.    Mean response accuracies and latencies for

rule retrieval on the repeat-three-times task

	Response accuracy (%)	Reaction time (s)
Pre-test	45.00(1.7)	2.39(0.05)
Post-test	95.97(0.7)	2.35(0.04)
Long-test	97.78(0.5)	1.66(0.04)

• B.    fMRI data

FMRI was used to investigate memory stability under the condition of known background knowledge. The fMRI trail (e.g. P→Q) was simpler than the training trail (e.g. P→Q↑P), which took place outside of the scanner and expected those operations were manipulated. The subject performance task in the fMRI scanner comprised the stability effects of over-learning responses, which was responsible for the effect observed in Experiment 3 (Table 3). Note that the regions with activity correlated with the fact memory task rule. The subjects were not required to understand visual objects, but to rather retrieve a rule, which was considered related to maintenance, and not calculation, processes.

Consistent with previous studies [21, 22], memory stability-dependent activity was obtained for single features of rule representation, as well as retrieval in the left inferior parietal lobule and left inferior frontal gyrus. Activity in the inferior parietal lobule (Fig.2A) was also dependent on stabilized memory for all rules. When the core systems of number-processing were compared with stable memory of Boolean rules, the activation on the same regions was observed within the left inferior frontal gyrus (Fig. 2B). When retrieval rules the activation regions were obtained within whole brain (Fig. 2C).

W. Discussion

The result of the stabilized memory was consistent with that of the arithmetic facts. Thus, activity in the same left inferior parietal lobule, as did the activity in the inferior frontal gyrus, which was expected to be a stable condition included retention of rule information. More importantly, there were additional brain areas showing stability-dependent activity when features from the rules were maintained. Activity in the inferior parietal lobule, which has previously been shown to be advantageous to stable memory for tasks defined by strategy and rule, was load dependent on memory of symbol representation.

TABLE III.    Regions of activation (in talairach space)

during all the retrieval rules relative to rest (intertrial interval)

	Region	BA	x y z	z-score	voxels
L	IFG/Insula	47/13	-33 20   -4	5.88	513
L	Th/PG	/27	-21 -35   2	5.51
L	Th/Caudate		-18 -20 15	5.37
R	LN		21    -9     3	5.29	266
R	LN		12   -3    -2	5.19
R	IFG	47	36   20   -9	5.14
L	PoG	2/1	-53 -24 51	5.28	537
L	MFG	6	-33   2   47	5.23
L	IPL/PoG	40/2	-48 -27 43	5.12
R	Posterior lobe	18	18 -63 -32	5.24	450
L/R	Declive		0   -74 -16	5.12
R	LG	18	9   -79     1	5.11
R	Culmen		21 -47 -15	5.06	90
R	Declive/FG /PG	19	27 -59   -7	4.94
R	LG/FG	18,19 /19	24 -70   -4	4.91

L: left; R: right; BA: Brodmann’s regions; IFG: Inferior frontal gyrus; Th: Thalamus; PG: Parahippocampal gyrus; LN: Lentiform Nucleus; IFG: Inferior frontal gyrus; PoG: Postcentral gyrus; MFG: Middle frontal gyrus; IPL: Inferior parietal lobule; LG: Lingual gyrus.

The present study provided evidence that experience-dependent stability in human mathematics was accompanied by modulations within the network of regions recruited during encoding. First, abstract mathematical rules, which require stronger retrieval capacity, and stress symbolic and concrete depictions were linked together in the processing regions, which should exhibit larger brain activity in fronto-parietal regions compared with number-processing tasks that merely induce recall of exact arithmetic facts. These regions have been repeatedly observed in response to relational numerical calculation tasks in adults [22-24], and have been shown display differential activation depending on the arithmetic problems [25, 26]. Previous lesion and imaging studies of arithmetic operations have demonstrated the importance of the inferior parietal lobule in arithmetic processing [23, 27]. Exact arithmetical facts (e.g., 2+3) are stored and maintained in same, but have also been associated with inferior frontal [28] and subcortical areas [25]. Second, previous studies have demonstrated the contribution of language in the retrieval of arithmetic facts [29]. Some studies have proposed that the parietal brain circuit is associated with language production and comprehension for storing and retrieving arithmetic facts [3, 30]. Both hypotheses have been verified, including similar modifications of brain activation for all trained rules and activation associated with core systems of number. When more response regions from these rules were compared with arithmetic facts, results confirmed that complex tasks proceed through more cognitive steps. Boolean rules vs. number-processing tasks previous studies were compared with identify common activations. fMRI data suggested that the partial cortex interacts with other regions to format of stabilized memory, which involved the extending of processing of arithmetic facts [22]. Although former studies did not compare advanced mathematics to basic number-processing, the present results suggested that the fronto-parietal regions may serve to increase knowledge based on arithmetical facts. For example, Fehr et al. [31] suggested that more difficult arithmetic problems require combined arithmetic facts, which activates the parietal regions [10]. Based on these data, Dehaene et al. [6] proposed that the source of mathematical thinking composes of linguistic and visual-spatial neural circuits, both of which are necessary for arithmetic processing. Activation in the left inferior parietal [32] and left parietal regions [33] has been shown to be activated in number-processing studies.

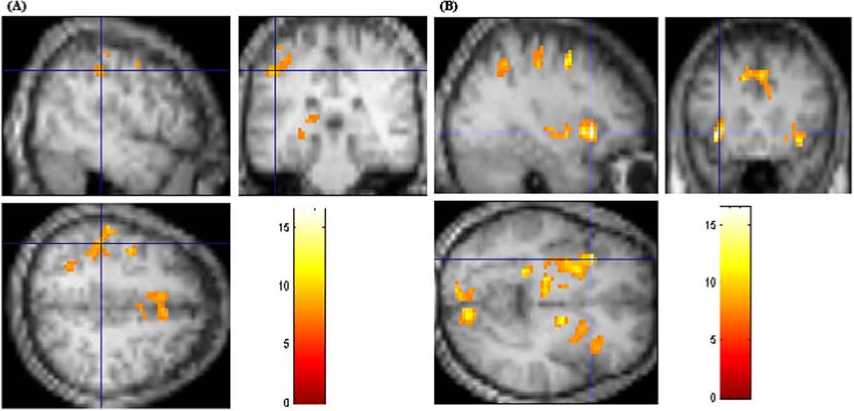
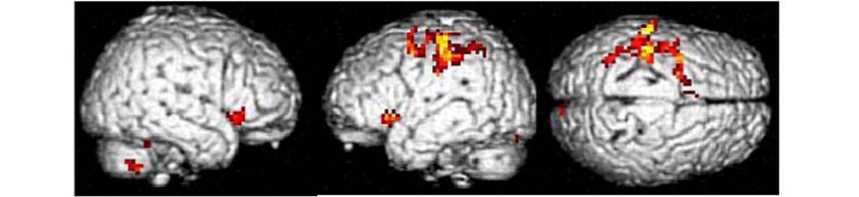
Fig. 2. (A) Two-dimensional significant activation in the left inferior frontal gyrus (Talairach: x=-33, y=20, z=-4). (B) Two-dimensional significant activation in the left inferior parietal lobule (Talairach: x=-48, y=-27, z=43). (C) Three-dimensional rendering of significant cortical activation for the random effects group analyses for memory stability of Boolean rules, p <0.00001.

Only a few studies have explored the relationship between rote arithmetic facts and correlative, different arithmetic operations. Fehr et al. [31] determined, through the use of fMRI, that the inferior parietal and inferior frontal was activated by complex arithmetic operations, compared with simple arithmetic facts. In addition, all complex arithmetic operations tasks and simple arithmetic facts exhibited common activation in the fronto-parietal regions. The present data indicated that rule retrieval tasks also exhibited the left fronto-parietal activations, when compared with simple arithmetic facts. These results emphasized the importance of background knowledge, especially when studies address complex mathematical problems. The present results provided evidence for memory stability that relies on core systems of number during the mental arithmetic in adults. During retrieval of Boolean tasks, for which stabilized memory was comparable to systems of number-processing, identical and different regions were activated. This suggested disparate levels and cortices of functional maturation in particular brain regions, based on core systems of number-processing. Long-term trained subjects exhibited activation in the left inferior parietal lobule and left inferior frontal gyrus. These areas have been consistently activated, with a fixed effected statistical map for sustained activity in the core systems of number-processing [34], and have been implicated in simple number-processing deficits due to fronto-parietal lesions [35]. Long-term trained subjects also exhibited activation in the left fronto-parietal, which are thought to be important for increased automaticity [36]. These findings suggested a process of increased stability of the left fronto-parietal regions with core mechanism.

This study provides background information about potential influences on stability-dependent activation, which helps to further emphasize the interpretation of the present findings. Stability-dependent functional activation clearly involved the core systems, which suggested that stability-dependent functions appear to be a consequence of maturing neural systems. This study provides evidence for stable memory in rule-based Boolean arithmetical tasks. Because the core systems are the most fundamental stable cognitive systems that adults prossess [37], the implications of the present findings are potentially wide-ranging. Also, images data help to understand the interrelationship between background knowledge and new arithmetic knowledge, and elucidate “the laws of experience-based learning”[38].

• V. Concluding Remarks

The aim of the present study was to investigate memory stability of Boolean rules in adults, and to determine whether these high-level skills accounted for performance based on the core systems of number. According to the core systems of number described by [4] results were consistent with retrieval of arithmetic facts [6, 30]. Consistent with our predictions, analysis of the behavioral data revealed that adults with stable memory performed better than those under the control of instable memory rules. Similarly, adults with stable memory executed mental arithmetic strategies significantly faster and exhibited increasing automation with regard to retrieval of arithmetic facts [38]. In conclusion, adults with stable memory exhibited the development of mathematical fact knowledge, culture background, and conceptual understanding, which were not mutually exclusive. Based on the model of Feigenson et al.’s [4] model, analyses revealed specific associations between rule processing and background knowledge. Based on previous studies focused on the cultural abilities of number-processing, the present results provided a better understanding for the origins of some key domains of the human mathematic culture.

Acknowledgment

This work was supported by Doctor Start-up Fund of Harbin Normal University (No. KGB201013), and Philosophy Social Sciences Program of Heilongjiang Province of China (No. 10B037). Furthermore, we are especially grateful to Erik, H.Q. Tu, L.L. Ding and one anonymous reviewer, who gave some suggestions that improved the manuscript.