The strategy of coordinated pursuit for a first-order differential game with Gronwall-Bellman constraints
Автор: Doliyev O.B.
Журнал: Мировая наука @science-j
Рубрика: Основной раздел
Статья в выпуске: 9 (90), 2024 года.
Бесплатный доступ
In this work, we will consider a simple pursuit differential game of the fitst order when Gronwall-Bellman constraints imposed on control functions of the players. The proposed method substantiates the parallel approach strategy in this line differential game of the fitst order. The new sufficient solvability conditions are obtained for problem of the pursuit.
Differential game, geometrical constraint, gronwall-bellman constraint, evader, pursuer, strategy, parallel pursuit
Короткий адрес: https://sciup.org/140306454
IDR: 140306454
Текст научной статьи The strategy of coordinated pursuit for a first-order differential game with Gronwall-Bellman constraints
Let in the space R” the controlled object P (the pursuer), chases another object E (the evader). Suppose Л and У are the locations of the pursuer and the evader respectively, and Wo (*o * Jo) are their initial locations. The motions of the objects are described by the equations
P : x = и, x(0) = x0,
E: y = v, j(o)= v0, where x,y,u,v e R \ n > 2.
In the present, the concept of the first type of Gronwall-Bellman constraint [1] for the control w(‘) is introduced in the form
|w(/)|2 ^ p1 +2j/^)|w(^)|2 ds, 0
-negative number and i ^s^ is a non-negative function. The first type of where p is a non
Gronwall-Bellman constraint generalizes geometrical constraint when /(^) = O.
Similarly, the concept of the first type of Gronwall-Bellman constraint for the control v0 is introduced in the form
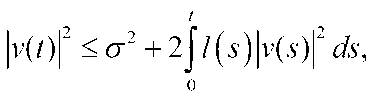
-negative number and i ^s^ is a non-negative function where a is a non
Here, и is the velocity vector of the pursuer and here the temporal variation of и must the set of all measurable
GB
be a measurable function w(-): [0, + oo) ^ R" We denote by U functions ^(’) satisfying Gronwall-Bellman constraint (3) (briefly, GB -constraint)
Similarly, v is the velocity vector of the evader and here the temporal variation of v must be a measurable function v(-):[0,+oo)->R". We denote by V(
GB
the
set of all measurable functions v(') satisfying the GB -constraint (4)
Definition 1. For a pair of is,
^O,W0), w(-)eUGS the solution of the equation (1), that
x(/) = x0 + ^i/^s)ds is called a trajectory of the pursuer on interval Z > 0
Definition 2 . For a pair of(.УоХ-)), v(-)eVG5 the solution of the equation (2), that is,
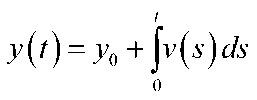
is called a trajectory of the evader on interval
Definition 3. The pair of classes of admissible controls introduced
(^ GB ? ^GB ) defines differential game (1)-(4) with constraints of the Gronwall-Bellman type or briefly, GB -game.
Definition 4. In the GB -game, the pursuit problem is called to be solved if there exists such control function

of the pursuer for any control function

of the
evader and the following equality holds at some finite time [
x(O = y(t ) .
Definition 5. If Р>(У, then
1^bM = v-\;bM^
is called ^ ^ GB -strategy of the pursuer ([3]-[4]) in the
GB -game,
where
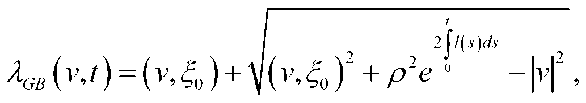
product of the vectors v and ^0 in the space R .
zo and
is the
scalar
Note that
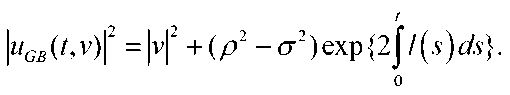
Lemma 1. (of Gronwall-Bellman). If
|®(/)|2 < cr + 2 j/(^)|ffl(5)|' ds, then
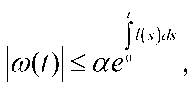
where G)(t\ / >0 is a measurable function and (X is a non-negative number and^ ^^ ^ is a non-negative function
Now we will introduce a notation
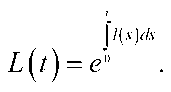
Property 1. If р>ф then the function ^GB ^^ is continuous, nonnegative and defined for all the control functions V(') such that satisfies the GB -constraint (3)
Property 2. If P>C>, then the following inequality is true for the function
Theorem. If p>a and l(s)>0 in the Gr -game, then the П -strategy of the player
P is winning on interval [0. 7U where ^GB is a positive solution of an equation
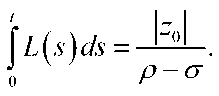
Proof. Suppose the pursuer choose the strategy (6) when the evader chooses any control function 'O G Ngb • Then according to the equations (1)-(2), we have the following Cauchy problem:
:0, z(0) = z0.
Thus the following solution is found by the given initial conditions or
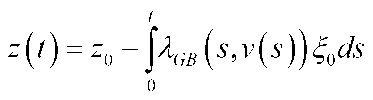
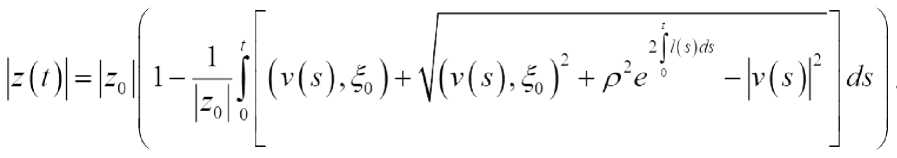
According to the properties (1)-(2), we will form the following inequality
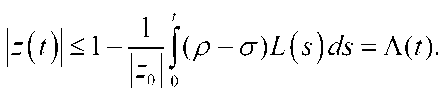
By solving an equation л(о = о we get a positive solution ^GB
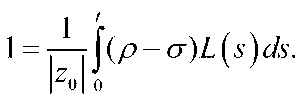
From this, we have
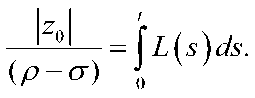
This finishes the proof of the theorem
Список литературы The strategy of coordinated pursuit for a first-order differential game with Gronwall-Bellman constraints
- Gronwall T.H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations. Ann. Math., 1919, 20(2): 293-296.
- Azamov A.A. About the quality problem for the games of simple pursuit with the restriction, Serdika. Bulgarian math. spisanie, 12, 1986, - P.38-43.
- Azamov A.A., Samatov B.T. П-Strategy. An Elementary introduction to the Theory of Differential Games. - T.: National Univ. of Uzb., 2000. - 32 p.
- Azamov A.A., Samatov B.T. The П-Strategy: Analogies and Appli-cations, The Fourth International Conference Game Theory and Management, June 28-30, 2010, St. Petersburg, Russia, Collected papers. - P.33-47.
- Azamov A., Kuchkarov A.Sh. Generalized 'Lion Man' Game of R. Rado, Contributions to game theori and management. Second International Conference "Game Theory and Management" - St.Petersburg, Graduate School of Manage-ment SPbU. - St.Petersburg, 2009. - Vol.11. - P. 8-20.
- Azamov A.A., Kuchkarov A.Sh., Samatov B.T. The Relation between Problems of Pursuit, Controllability and Stability in the Large in Linear Systems with Different Types of Constraints, J.Appl.Maths and Mechs. - Elsevier. - Netherlands, 2007. - Vol. 71. - N 2. - P. 229-233.
- Barton J.C, Elieser C.J. On pursuit curves, J. Austral. Mat. Soc. B. - London, 2000. - Vol. 41.- N 3. - P. 358-371.
- Borovko P., Rzymowsk W., Stachura A. Evasion from many pursuers in the simple case, J. Math. Anal. And Appl. - 1988. - Vol.135. - N 1. - P. 75-80.
- Chikrii A.A. Conflict-controlled processes, Boston-London-Dordrecht: Kluwer Academ. Publ., 1997, 424 p.
- Fleming W. H. The convergence problem for differential games, J. Math. Anal. Appl. - 1961. - N 3. - P. 102-116.


