Theory of Fuzzy Sets: An Overview

Published Online September 2013 in MECS

In most cases of our life, data obtained for decision making are only appropriate. Zadeh [1] introduced the concept of fuzzy set theory to meet those problems. The fuzziness can be represented in different ways; one of the most useful representations is the membership function. Fuzzy set theory generalizes the conventional set theory; therefore it is considered that its axiomatic foundation is unavoidably difficult from that of classical set theory. More specifically, it has to violate the two fundamental laws of Boolean algebra- the law of contradiction AA^c = ∅ and the law of excluded middle AA^c = Ω . In other words, it is possible for an element to partially belong to both a fuzzy set and set’s complement. The reason behind such a claim can be contributed to the fact that the complement of the fuzzy set a is defined by the membership function

µ _A ^c ( x ) = 1 - µ _A ( x ), ∀ x ∈ Ω (1)

This definition of complementation of fuzzy set has numerous applications. Various theories have been developed all of which cannot be covered in this article. Here for illustration purposes, we would name a few. These are cardinality, entropy, subsethood theorem and also in the case of fuzzy matrices. Similarly, we have found some drawbacks in the results obtained by various researchers working in the field of probabilitypossibility consistency.

The main purpose of this article is to convey that the aforementioned way of representing the complement of fuzzy sets as well as the consistency principles established so far can never give us the desired result. It seems that the existing definitions were not proposed within appropriate mathematical frameworks. In most cases of practical significance, it is desirable to consider an additional requirement for defining fuzzy complement to make it logical. This realization led Baruah ([2]-[8]) , to propose that the most desirable requirement in defining the correct complementation is the use of reference function and also the existence of two laws of randomness is required to define a law of fuzziness.

The rest of the paper has been organized as follows: Section II deals with the definition of complementation of fuzzy sets based on reference function. Section III provides some results of fuzzy sets and some new results are introduced on the basis of reference function. Section IV gives results found by the use of the existing probability-possibility consistency principles. Section V provides the Randomness-Fuzziness Consistency principle and its uses in finding the entropy of fuzzy numbers. Finally, Section VI deals with our conclusions.

Before embarking n deeper study on various aforementioned theories of fuzzy sets, let us reflect a little on the new definition of fuzzy sets put forward by Baruah. This can be described as follows:

• II.    Baruah’s Definition of Complementation of Fuzzy Sets

Baruah ([4], [5]) defined complement of a fuzzy set with the help of two functions: a membership function and a reference function. The differene between the two gives the membership value which plays a central role in defining fuzzy sets especially the complementation of fuzzy sets.

In accordance with the process discussed above, a fuzzy set defined by

A= {x, µ(x), x∈Ω} would be defined in this way as

A= {x, µ(x), 0, x∈Ω}

So that the complement would become

Ac ={x,1,µ(x),x∈Ω}

This definition of complementation of fuzzy sets leads us to conclude that unlike crisp sets fuzzy sets also obey excluded middle laws.

Symbolically these can be expressed as

A П A^c = 0

and

A U A^c -Q                           (5)

It is important to mention here that the new definition of complementation does satisfy almost all the properties of fuzzy sets except the two most debatable laws. As we see that the new definition performs precisely as the corresponding operation on crisp sets, it in fact challenges the most sacred elements of the foundation- fuzzy sets violate the excluded middle laws, which has ben taken for granted from the inception of the theory and viewed as inviolable.

Application of the existing definition of fuzzy sets is quite extensive particularly in those endeavours concerned with cardinality, entropy, subsethood as well as fuzzy matrices. The motivation for the application of the new definition lies in the need to handle some illogical conclusions.

So in this article, we would like to focus our attention to some of the theories of fuzzy sets with special reference to the cardinality, entropy, subsethood and fuzzy matrices. Let us have a brief look at these in the following sections.

• III.    Some Results of Fuzzy Sets

• 3.1    Cardinality of Fuzzy Sets

This section deals with some existing definitions and theories of fuzzy sets and their new definitions proposed which are in accordance with the theories developed by Baruah as the case may be.

In fuzzy set theory, we can see the use of the term cardinality which is most commonly used concept in many areas. Cardinality belongs to most important and elementary characteristics of a set. The cardinality of a crisp set is the number of elements in the set. Using fuzzy sets which are many-valued generalization of sets, one likes to have for them analogus characteristics. The concept of cardinality of fuzzy sets received a lot of attention from the researchers from the beginning of fuzzy set theory. Since an element can partially belong to a fuzzy set, a natural generalization of the classical notion of cardinality is to weigh each element by its membership degree, which gives us the following formula for cardinality of a fuzzy set. There are several approaches to the cardinality of fuzzy sets. One group of them had constructive approaches. Following these approaches, we get a single number or alternatively a fuzzy set as cardinality of fuzzy set. The first concept of this kind was proposed and discussed in De Luca and Termini [9]. In many applications, one prefers a simple scalar approximation of cardinality of a fuzzy set. Scalar cardinality of a fuzzy set is the sum of the membership values of all elements of the fuzzy set. In similar way fuzzy cardinalities of a fuzzy set that associate to any fuzzy set, a convex fuzzy natural number. But fuzzy cardinality of fuzzy sets is beyond the scope of this article. The scalar cardinality of a fuzzy set A is defined as follows:

A=∑µA(xi),x∈Ω this A is called the sigma- count of A.

It is important to mention here that since we would like to define fuzzy sets with the help of two functions such as fuzzy membership function and fuzzy membership value. In parallel with what had been done for cardinalities of fuzzy sets, we shall define the cardinality of a fuzzy set A as:

A = card ( A )

= ∑ { µ ₂( x ) - µ ₁( x )}, x ∈ Ω            ⁽⁶⁾

It can be easily seen that this new definition of cardinality satisfy the properties which were set for the existing definition, Dhar [10].

• 3.2    Entropy of Fuzzy Numbers

Fuzzy entropy is the measurement of fuzziness of fuzzy sets, and thus has an important position in fuzzy systems such as fuzzy decision making systems, fuzzy control systems, fuzzy neural network systems, and fuzzy management information systems.

Kosko ([11], [12]) has defined the entropy of a fuzzy set A as:

E(A) = A П Ac (7) A U Ac where AAc and AAc denote the cardinalities of the sets A П AC and A U Ac

And it is important to note here that the cardinality is defined in the following way:

IA = E Ma (x), X eQ

De Luca and Termini [6] suggested as a measure of fuzziness the “entropy” of a fuzzy set, which they defined as follows:

The entropy as a measure of fuzzy set A = { X , ^ _A ( X ), X e Q } is defined as

D ( A ) = H ( A ) + H ( A^c )                    (8)

n

H ( A ) = - K ^ m _a ( x , ) In p A ( x , )              (9)

j = 1

Where n is the number of elements in the support of A and K is a positive constant.

Yager [13] argued that the measure of fuzziness should be dependent on the relationship between the fuzzy set A and its complement A^c .Then he suggested that the measure of fuzziness should be defined as the lack of distinction between a and its complement A^c . Yager defined a measure of fuzziness of A in the following manner:

D ( A , A^c )

f_P ( a ) = 1 — и     _r J                  (10)

sup p ( A )

Where n1

D p ( A , A^c ) = [X| M a ( x , ) "I A a c ( x , )] ^p        (11)

i = 1

where A^c stands for the complement of the set A.

• 3.3    Cartesian Product of Two Fuzzy Sets

Let     A ₁, A ₂,........., A_n   be fuzzy sets in

Q , Q ,, Q„    respectively. The cartesian

• 1 ,    2 ,             , n

• 3.4    New definition of Cartesian Product of Fuzzy Sets

product of A ₁, A ₂,........., A_n is fu zzy set in the space

M ₄x A 2 XX A „ ^{( X} 1 , ^X 2 ,, ^X n )

= ^min( M A ^{( X} 1 ), M a ^{( x} 2 ),......, M a ^{( x} 1 ))

So, the cartesian product of A1, A2,........., An is denoted by

A x A xx A

Let A A......... Abe fuzzy sets defined in terms 1, 2,, of reference function in   Q, Qo,, Q„ respectively. The cartesian product of A1,A2,.........,An is fuzzy set in the space

^M A , X A ₂ X.........X A_n ^{( x} 1 , ^X 2 ,........ , ^X n )

= min( Ma (X1), Ma (x 2),......, Ma (x„)), max( mA (X!), mA (x 2),......, mA (x„)}

Where   mA (Xi), mA (X 2),......, mA (Xn )  are the reference functions of the fuzzy sets A1, A2,........., An

We would like to discuss it in the following way

Let us consider two fuzzy sets expressed according to the new definition as

A = {u i, Ma (u i), Ma ■ (U)} and

B = ^{ vi, M b ⁽ v , ), Mb ' ⁽ v , ^)}

Then their cartesian product would be presented as

A x B =

⁽ Ц а ⁽ u i ), Ц д, ⁽ u i )) (M_A ⁽ u 2 ), Ma'⁽ u 2 )

^x( M b ⁽ v i ), Mb ■ ⁽ v i ))

⁽ M b ⁽ v 2 ), M b■ ⁽ v 2 ))•••   ⁽ M b ⁽ V ), M b' ^{( v} n ) )

( ⁽ M a ⁽ u n ), M a⁽ u n )) )

For usual fuzzy sets we are to consider

M a ■ ⁽ u i ) = M a - ⁽ u 2 ) == M a • ⁽ u n ) =0

and also

Mb'(vi) = Mb'(v2) == Mb'(vn)=0

would be represented as in the following way according to Dhar [27]

	' ( a i ,0)	( b 1 ,0)	( c 1 ,0)
B =	( a 2 ,0)	( b 2 ,0)	( c 2 ,0)
	v ( a 3 ,0)	( b 3 ,0)	( c 3 ,0)

• 3.5    Fuzzy Matrices

It is well known that the matrix formulation of a mathematical formulae gives extra advantage to handle/study the problem.When the problems are not solved by classical matrices, the concept of fuzzy matrices are used. Matrices with entries in [0, 1] and matrix operation defined by fuzzy logical operations are called fuzzy matrices. All fuzzy matrices are matrices but every matrix is not a fuzzy matrix. Fuzzy matrices were introduced first time by Thomson who discussed the convergence of powers of fuzzy matrices. Fuzzy matrix has been proposed to represent fuzzy relation in a system based on fuzzy set theory. Just as a classical relation can be viewed as a set, fuzzy relation can also be viewed as a fuzzy subset.

In this article, we would like to suggest a fuzzy matrix representation based on reference function. Furthermore, new definitions for trace of a fuzzy matrix, determinant and adjoint of fuzzy matrices along with some properties associated with this definition is also suggested .It is important to mention here the fact that we would discuss about these in brief as these have been discussed in more details in our previous work (see for example Dhar ([20]). Let us have the following few lines as support of the statement.

Accordingly, for the a square fuzzy matrix of order 3

	^ a i	b 1	C i'
B =	a 2	b 2	c 2
	( a 3	b 3	C 3 V

And then the complement of the above matrix will be written as

Bc

( (i, a j   (i, b i )   (i, C i ) ^

(i, a 2 )   (i, b 2 )   (i, c 2 )

( (i, a 3 )   (i, Ь з )   (i, c 3 ) J

• 3.6    Transpose of a Matrix

Let A = [( a jj , 0)] be any fuzzy matrix. Then the m X n matrix obtained from A by changing its rows into columns and columns into rows is called the transpose of A and is denoted by the symbol A ' .

Symbolically, if

A = [( a_y -,0)]

Then B = [( Ь ^ , 0)] where b ^ = a ^

That is (j, i) th element of A is equal to the (i, j) th element of A.

If A' and B' be the transposes of A and b respectively, then the following properties hold

• (i)    ( A ' ) ' = A

• (ii)    ( A + B ) ' = A ' + B' , A and B being of the same size.

• (iii)    ( A • B ) ' = B ' • A ' , A and B being conformable for multiplications.

Proof

• (i)    Let A be a m X n matrix. Then A ' will be a П X m matrix. Therefore ( A ') ' will be a m X n matrix. Thus the matrices A and ( A ' ) ' are of the same type.

Also (i, j) th element of ( A ')

= (j, i) th element of A'

= (i, j)th element of A

Hence ( A ') ' = A

Let us consider the following example

Then

	( (0.1,0)	(0.7,0)	(0.5,0)
A =	(0.2,0)	(0.8,0)	(0.7,0)
	, (0.5,0)	(0.3, 0)	(0.2,0)
	' (0.1,0)	(0.2,0)	(0.5,0)
A =	(0.7,0)	(0.8, 0)	(0.3,0)
	, (0.5,0)	(0.7,0)	(0.2,0)

Therefore

' (0.1,0)

( A ') '= (0.2,0)

This shows that

(0.7,0) (0.5,0)л

(0.8,0) (0.7,0)

(0.3,0) (0.2,0) v

( A ' ) ' = A

• (ii)    Let A = [( a y , 0)] and B = [( b y , 0)] . Then A+B will be a matrix of the type m X n and consequently ( A + B ) ' will be a matrix of the type n X m .

Again A ' and B ' are both of n X m matrices. Therefore sum A ' + B' exists and will also be of matrix of the type n X m

Further (i, j) th element of ( A + B ) '

= (i, j) th element of A+B

= {max ( a _j , b _j ), min (0, 0)}

= (j, i)th element of A* + (j,i)th element of B'

= (j, i)th element of A ' + B '

Thus the matrices ( A + B ) ' and A ' + B ' are of the same type and their (j, i)th elements are equal.

Hence

( A + B ) ' = A + B'

Let us consider the following numerical example to make the matter clear.

Let us consider two matrices A and B as follows

A = and	< (0.1,0) (0.7,0) (0.5,0) 1 (0.2,0) (0.8, 0) (0.7, 0) v (0.5,0) (0.3,0) (0.2,0) y				0) ^ 0) 0) J
	3 =	' (0.1,0) (0.2,0) ( (0.5,0)	(0.3, 0) (0.4,0) (0.3, 0)	(0.5, (0.7, (0.2,
Then we have
	^	(0.1,0)	(0.7,0)	(0.5,0)л
A + В =		(0.2,0)	(0.8, 0)	(0.7,0)
	\	(0.5,0)	(0.3,0)	(0.7,0) ,
		' (0.1,0)	(0.2,0)	(0.5	,0) )
( A + B ) ' =		(0.7,0)	(0.8,0)	(0.3,0)
		v (0.5,0)	(0.7,0)	(0.7	,0) J
Again we have
		f (0.1,0)	(0.2,0)	(0.5,	0) 1
A =		(0.7,0)	(0.8, 0)	(0.3,0)
		v (0.5,0)	(0.7,0)	(0.2,	0) J
		' (0.1,0)	(0.2,0)	(0.5,	0) 1
and B	'=	(0.7,0)	(0.4,0)	(0.3,0)
		v (0.5,0)	(0.7,0)	(0.2,	0) J
		' (0.1,0)	(0.2,0)	(0.5,	0) 1
A ' + B ' =		(0.7,0)	(0.8,0)	(0.3,0)
		v (0.5,0)	(0.7,0)	(0.2,	0) J

Hene we get

( A + B ) ' — A' + B'

A —

' (0.1,0) (0.2,0) "

_v (0.5,0) (0.3,0) _v

If we consider the complement of the above fuzzy matrices, we get

( A^c + B^c ) ' — ( A^c ) ' + ( B^c )'

	Ac —	(1,0.1) (1,0.2) (1,0.5)	(1,0.7) (1,0.8) (1,0.3)	(1,0.5) 3 (1 ,0. 7) (1,0.2) )
		< (1,0.1)	(1,0.3)	(1,0.5)"
and B c —		(1,0.2)	(1,0.4)	(1,0.7)
		< (1,0.5)	(1,0.3)	(1,0.2) ,
		' (1,0.1)	(1,0.3)	(1,0.5)	3
Ac	+ Bc —	(1,0.2)	(1,0.4)	(1,0.7)
		v (1,0.5)	(1,0.3)	(1,0.2)	/
		' (1,0.1)	(1,0.2)	(1,0.5)"
( Ac	+ B c ) ':	— (1,0.3)	(1,0.4)	(1,0.3)
		v (1,0.5)	(1,0.7)	(1,0.2),

Again	' (1,0.1)	(1,0.2)	(1,0.5)"
( Ac ) ' =	(1,0.7)	(1,0.8)	(1,0.3)
	v (1,0.5)	(1,0.7)	(1,0.2) ,
and	< (1,0.1)	(1,0.2)	(1,0.5)"
( Bc ) ' =	(1,0.3)	(1,0.4)	(1,0.3)
	< (1,0.5)	(1,0.7)	(1,0.2) >

Therefore

	' (1,0.1)	(1,0.2)	(1,0.5)"
( Ac ) ' + ( Bc ) ' =	(1,0.3)	(1,0.4)	(1,0.3)
	v (1,0.5)	(1,0.7)	(1,0.2) ,

Hence we get

( A^c + B^c ) ' — ( A^c ) + ( B^c )'

• (iii)    Let us consider two fuzzy matrices as

( ((0.1,0) (0.9,0) (0.3,0) 3

and B —

( (0.4,0) (0.6,0) (0.1,0) )

Then by the process of matrix multiplication we get

AB _— ( ((0.2,0) (0.2,0) (0.1,0) 3

( (0.3,0) (0.5,0) (0.3,0) ,

And thus

	" (0.2,0)	(0.3,0)л
( AB ) ' =	(0.2,0)	(0.5,0)
	v (0.1,0)	(0.3,0) v
Again	' (0.1,0)	(0.4,0) з
B ' =	(0.9,0)	(0.6,0)
	v (0.3,0)	(0.1,0) ,
	' (0.1,0)	(0.5,0) з
and —	v (0.2,0)	(0.3,0) v
Therefore (	(0.2,0)	(0.3,0) 3
B'A ' —	(0.2,0)	(0.5,0)
	(0.1,0)	(0.3,0) ,

Hence we have

( AB ) ' = B ' A

Similarly if we consider the complement of fuzzy matrices which are conformable for multiplication then we get

( AB' ) — ( B^c )'( A^c )'

• 3.7    Trace of a Fuzzy Matrix

The trace of a fuzzy matrix is defined as

Let A be a square matrix of order n. Then the trace of the matrix A is denoted by tr A and is defined as trA = (max и, min ri)

where p ii stands for the membership functions lying along the principal diagonal and r_ii refers to the refence function of the corresponding membership functions.

The following properties can be easily verified

Let A and B be two fuzzy square matrices each of order n and X be any scalar such that

0 < X < 1

Then

• (i)    tr (A+B) = trA+tr B

• (ii)    tr ( X A ) = X tr ( A )

(iii)tr A= tr A , where A is the transpose of A.

• IV.    Probability-Possibility Consistency Principle

Where k is a constant which gurantee the following condition of consistency:

V w е X: n( w) > p (w)

This condition is a particular case of Dubious- Prade consistency principle but there is a condition that the value of ‘k’ must belong to the following interval:

0 <  k <

log p_n

( 1 - P n ) • log p n p ₁

It was mentioned by them that this above mentioned transformation is different from Klir’s transformation in the sense that Klir’s transformation has a constant power which belongs to the open interval ] 0,1 [ while the power k (1 — p i ) in variable transformation , is a variable to make it more specific. But this transformation was discarded due the same reason, Dhar ([33]-[38])

Yager’s probability- possibility transformation is as follows:

Assume P is a probability distribution on X = { X i , X 2,........ , X n } where p 1 >  p 2 >........> P n .

^Uj = j ( p j - p j — 1 ) + ^U j + 1

It was mentioned that using the formula stated above he trasformation from probability distribution to possibility distributionwas derived.

Similarly assuming U 1 >  U 2 >

> U as a n

normal probability distribution on X with U 1 = 1 , they obtained an associated probability distribution on X where,

^Uj - ^Uj + 1 j

pn

u

= _and p j = p j + 1 + n

This transformation was discarded for the aforementioned reasons, Dhar ([24]-[28]).

It is for this reason; we would like to suggest the Randomness- Fuzziness consisyency principle introduced by Baruah [3]. Let us have a look at it in brief in the following section.

• V.  Randomness-Fuzziness Consistency Principles

Baruah [3] introduced a framework for reasoning with the link between probability – possibility. The developoment of this principle focused mainly on the existence of two laws of randomness which are required to define a law of fuzziness. In other words , not one but two laws of fuzziness is required to define a law of randomness on two disjoint spaces which in turn can construct a fuzzy membership function. Fundamental to this approach is the idea that possibility distribution can be viewed as a combination of two distributions of which one is a probability distribution and the other is a complementary probability distribution.

The consistency principle introduced in the manner can be explained mathematically in the following form:

For a normal fuzzy number of the type N = [ α, β, γ ] with membership function

μ ( x ) = Ψ 1 ( x ), if α ≤ x ≤ β ,

= Ψ2(x), if β ≤ x ≤ γ, and = 0, otherwise, with Ψ1 (α) = Ψ2(γ) = 0,

Ψ1 (β) = Ψ2 (β) = 1, the partial presence of a value x of the variable X in the interval [α, γ] is expressible as

μ ( x ) = θ Prob [ α ≤ X ≤ x ]

+ (1 – θ ) {1 – Prob [ β ≤ X ≤ x ]},           (9)

where θ=1 if α ≤ x ≤ β and θ=0 if β ≤ x ≤ γ

Thus from the above principle, it can be seen that a possibility space can be seen as a combination of two probability spaces, one to the left of maximum membership function and the other to the right of the membership function.

This principle plays a key role in defining entropy of fuzzy sets in the following manner:

• 5.1    New Definition of Entropy of Fuzzy Numbers

Keeping in view of the original definition of Shannon’s entropy which is defined as:

H ( P ) = - ^ PilnPi i =1, 2, .....,n.           (15)

i where p1, p2, , pn denotes the probabilities of n events, fuzzy entropy too can be defined by using the Randomness-Fuzziness Consistency Principle defined by Baruah [21]

Accordingly, the left reference function of a normal fuzzy number which is nothing but a distribution function, would lead to entropy E ₁ . In a similar manner, the right reference function of the normal fuzzy number, which is nothing but a complementary distribution function, would lead to another entropy E ₂ .The pair [ E ₁, E ₂] found can rightly be called fuzzy entropy in the classical sense of defining Shannon’s entropy for a discrete law of randomness. Discretizing a law of randomness for a continuous variable should not be of much problem, which in turn can be used to define fuzzy entropy [ E ₁, E ₂] , where E ₁ and E ₂ are Shannon’s entropies for the left reference function and right reference function respectively. This was discussed in more details in Dhar [30]. Some properties of fuzzy entropy which are the results of the new definition of entropy of fuzzy sets, Dhar [31] are listed below:

A triangular fuzzy number A= [a, b, c] expressed by the membership function

	x - a _
	----, a <  x <  b
	b - a
M a ( x ) = '	x - c , _ _ ----, b <  x <  c
	b - c

0, otherw se

The left reference function x- a being a distribution b - a function would give rise to entropy E and the right reference function x-c , which is a complementary b - c distribution function would give rise to an entropy E .

Thus we shall get a pair of entropy for a fuzzy number with one maximum.

But for a trapezoidal fuzzy number which is expressed in the form A= (a, b, c, d)

A trapezoidal fuzzy number A is defined by the membership function

Ц а ( X ) = «

x - d „ „ -----, C < X < c - d

0, otherwise

It can be seen very easily that for the part lying in b <  X <  C , the membership function is equal to 1 for this interval and this is a case of uniform distribution.

So here the probability density function is equal to 1 and this shows that the probability lying in this c - b part is

c ₁

b c ^{- b}

= 1

This can be expressed in the way that for the part lying in the interval b <  X <  C , the probability is equal to 1 and hence from Shannon’s entropy formula we get the entropy of the interval of unit presence obtained from the Shannon’s index as

H (p )=-E PiIn (p--)

i

= -(1 In1)

Hence it can be said that in b <  X <  C , we shall get no entropy. Thus the entropy of trapezoidal fuzzy number can be expressed in the form ( E ₁,0, E ₂) .

Some properties of entropy of triangular fuzzy numbers and trapezoidal fuzzy numbers are observed due to the use of the new definition of entropy of fuzzy sets, Dhar [24] which are listed below:

• 5.2    Properties of Entropy of Fuzzy Numbers

  • 5.2.1    Property1

• 5.2.2    Property2

• 5.2.3    Property3

• 5.2.4    Property4

• 5.2.5    Property5

• 5.2.6    Property6

• 5.2.7    Property7

Entropy of all triangular fuzzy numbers is the same for the same choice of the length of the interval.

The image of a triangular fuzzy number is again a triangular fuzzy number and hence the entropy of a triangular fuzzy number and its image are the same.

Entropy of the sum of two fuzzy numbers A+B is the same as that of the numbers A and B for the same choice of intervals.

The entropy of the difference of two fuzzy numbers A and B is the same as that of the individual entropies of the fuzzy numbers A and B.

The result from multiplication or division is not triangular fuzzy numbers and so the entropies obtained from multiplication or division will not be same as that of the individual entropies of the two triangular fuzzy numbers under consideration.

Addition of two trapezoidal fuzzy numbers becomes trapezoidal fuzzy number and hence the entropy of the sum of two trapezoidal fuzzy numbers is the same as that of the individual entropies of the two trapezoidal fuzzy numbers under consideration.

Subtraction of two trapezoidal fuzzy numbers is again a trapezoidal fuzzy number and hence the entropy of the difference of two trapezoidal fuzzy numbers is the same as that of the individual entropies of the two trapezoidal fuzzy numbers under consideration.

It is important to mention here that multiplication, division and inverse of trapezoidal fuzzy numbers need not be trapezoidal fuzzy numbers. But in many cases, operations resulting from multiplication or division are approximated to be of trapezoidal shape. If the approximate shape is taken into consideration then we would get the entropy of the multiplication or division of two complex numbers to be approximately equal to the concerned numbers otherwise we get different entropy.

So nothing can be said properly regarding the entropy of multiplication and division of trapezoidal fuzzy numbers.

Let us consider the following example cited in Lee [33], to make it clear and simple.

Let A=(1,5,6,9) and B=(2,3,5,8) be two trapezoidal fuzzy numbers.

We use α-cut intervals

A _a = [4 a + 1, - 3 a + 9] and

Ba = [a + 2, -3a + 8]

Since a e [0,1] , each element for each interval is positive, and the multiplication between α-cut

For a = 0

A o • B о = [2,72]

For a = 1

A₁ • B 1 = [15,30]

Now using four points in a = 0 and a = 1 , we can visualize the approximated value as the trapezoidal fuzzy number.

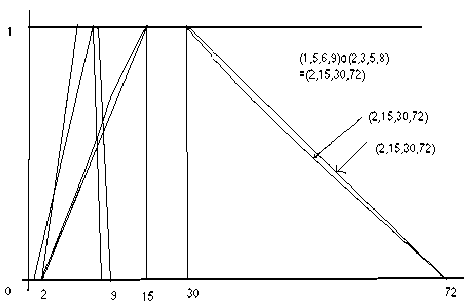
Fig. 1: Multiplication of two trapezoidal fuzzy numbers

It is important to note here the fact that if we consider non-triangular fuzzy numbers then the above mentioned properties donot hold always.

• 5.3    Fuzzy Ranking

Ordering of fuzzy quantities is based on extracting various features from fuzzy sets. A particular fuzzy set ranking method extracts a specific feature from fuzzy sets and then ranks them based on that features. Different procedures are available which may be based on centre of gravity, an area under the membership function, or point of intersection of various other poits between fuzzy sets. A brief survey of the various available ranking methods are discussed below.

Yager [34], proposed a ranking index which is based on the area under the membership function. Yager’s index is expressed as

Y ( A ) =

J g ( x )M a ( x ) dx

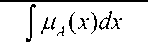
where g(x) is the measure of the importance of the value of x.

WCoG =  -- ^A---

I и A (x) dx where the quotient q is used to put more weight on higher membership values.

Cheng [37], developed distance method similar to WCoG as

_   J xu. (x) dx    _   J x^A \x) dx x0     Г            and y0     *    "

J цА ( x) dx           J цА-1( x) dx where the inverse of ЦА (x) is ЦА 1 (x) .

It is important to note here that all the methods discussed above for ranking of fuzzy numbers have some shortcomings if these are looked from the Randomness-Fuzziness Consistency principle. This principle states that a fuzzy number is expressible as a combination of a distribution function and a complementary distribution function. If this be the case, then the integration of distribution functions for ranking of fuzzy numbers are meaningless tasks. Hence the aforesaid methods for ranking fuzzy numbers are illogical from our standpoints.

• VI.    Conclusions

The main purpose of this article is to revisit and comment on some of the results associated with the existing definition of complementation of fuzzy sets.These results are discussed from the standpoints of the new definition of complementation of fuzzy sets on the basis of reference function and some new definitions are put forward whenever possible. Furthermore, we have discussed the three existing probability-possibility consistency principles and listed some drawbacks found in the process.Accordingly, the results obtained with the help of these principles are also not free from defects.It is for this reason , the Randomness-Fuzziness consistency principle is suggested hereby. Along with these some properties of the entropy of triangular as well as the trapezoidal fuzzy numbers are discussed herein. Further, the methods of ranking fuzzy numbers are rejected because these are obtained by integrating distribution functions from our perspectives and so further studies are required in this respect to find an appropriate method for ranking fuzzy numbers.

Acknowledgements

The authors would like to thank the anonymous reviewers for their careful reading of this article and for their helpful comments.