Three-dimentional modelling of external mechanical effects on devices and machinery in SolidWorks Simulation

Introduction. At present, when developing radioelectronic and electronic equipment, much attention is paid to the creation of three-dimensional models of devices. This allows you to reduce the cost of breadboard design and development time, to identify weak points, to develop recommendations for strengthening the design and to give a preliminary conclusion about the resistance of the device to loads. In this regard, numerical modelling is widely used in the design as an initial stage of complex testing of devices. With the help of specialized software the problems of strength, stability, dynamics, composites mechanics, hydrodynamics and heat transfer are solved [1–13].

The specific features of the devices, being developed in the Research and Production Center “Polus”, is that they must be rigid and strong. The load-bearing elements of the structure consist of plates and frames. In conditions of weight limitations, it is necessary to ensure the structural strength of devices and machinery in accordance with the specification.

Thus, the purpose of this work is to analyze the design of the device for resistance to external mechanical effects.

The analysis extends to the automation unit (AB). Mechanical loads are defined according to the specifications. The analysis was carried out by means of the SolidWorks software [14; 15].

The design of the automation unit (AB). According to the dimensional outline the AB has dimensions 340×200×200 mm and weight (6.7 ± 0.2) kg.

The automation unit is structurally composed of four unified bases of the torque control channels (TCC) and a filter located on the upper surface of the TCC, tightened at the corners by pins. The cases of the TCC are made of the alloy MA2-1 State Standard 21990–76 and have a wall thickness of 2 mm and a base of 3 mm. On each of the four bases, PCBs of glass fiber textolite STF-2-35-OS technical specification TU 16-503.161–83 are pressed. The side surfaces of the AB are covered with covers of the alloy MA2-1 State Standard 21990–76 with the thickness of 3 mm. To mount the device on its body on both sides there are six mounting feet.

Finite element model of the device. The modelling process begins with the creation of a geometric model of the AB (fig. 1), performed in accordance with the set of design documentation. In the model there are no elements that lack the effect of strengthening of the structure, but

their mass and the mass of radioelectronic devices are taken into account.

The software automatically creates a combined grid on a geometric model (fig. 2). The number of grid nodes is 1 501 193, and the elements – 888 873. The quality of the grid is determined by means of the Jacobian. For the given grid with a minimum (2 mm) and maximum (25 mm) side dimensions of its elements, the Jacobian is 29.4 (fig. 3). Its acceptable value is considered not more than 40.

The following material parameters were taken into account in the analysis (tab. 1): density; Poisson’s ratio; modulus of elasticity (Young’s modulus); tensile yield strength; strength limit.

The requirements for resistance to external effects. In accordance with the requirements specification the device must remain operational after various mechanical effects. During the modelling quasi-static effects, impact loads specified in the form of a shock spectrum and random and sinusoidal vibrations were used.

Modal Analysis. The eigenfrequencies, forms (modes) of vibrations of the AB model (fig. 4–6) and the resulting coefficient of mass participation are determined by the modal analysis (fig. 7).

Modelling of quasi-static effect and sinusoidal vibration. Border conditions:

– all elements of the model have a global contact with one another;

– the effect of gravity (acceleration of gravity) is taken into account;

– type of material model – linear, elastic, isotropic;

– the device is rigidly fixed over the entire surface of the mounting feet;

– the impact is applied to the base of the model consecutively in each of the three mutually perpendicular directions.

The natural frequencies of the AB model, obtained as a result of the modal analysis, exceed 150 Hz. Therefore, the calculation of sinusoidal vibration can be replaced by calculation for a quasi-static effect, since the stress arising in the elements of the model under the effect of a sinusoidal vibration will correspond to the stress under quasi-static loads.

In the case of quasi-static effect on the AB model, the maximum stress appears in the bases of the TCC (tab. 2).

As a result of the calculation, the values of the maximum stress and displacements under the effect along each of

the three mutually perpendicular directions were obtained.

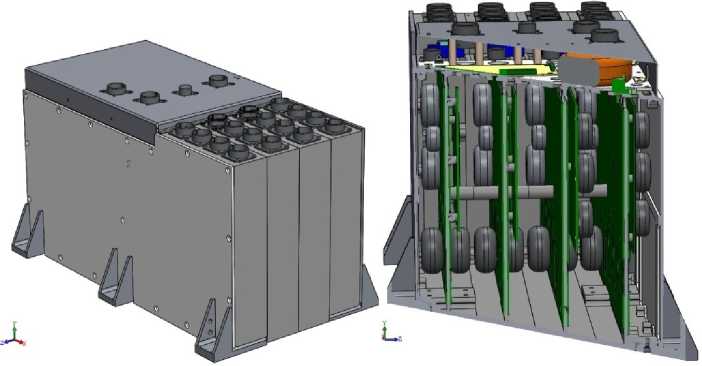
Fig. 1. Geometrical model of automation block (AB)

Рис. 1. Геометрическая модель БА

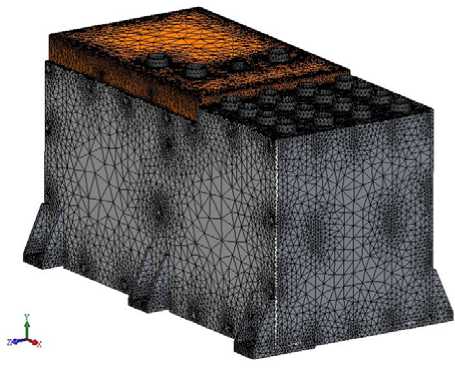
Fig. 2. A grid on geometrical model AB

Рис. 2. Сетка на геометрической модели БА

Fig. 3. Jacobian distribution

Рис. 3. Эпюра якобиана

Table 1

Material parameter	Parameter value
	Steel 10 shorttime strength, State Standard 1050–88	Magnesium alloy MA2-1, State Standard 21990–76	Aluminum alloy AMg6 2, State Standard 21631–76	Glass textolite, STF-2-35-OS technical specification TU 16-503.161–83
Density kg/m3	7 856	1 790	2 640	1700
Elastic modulus MPa	186 000	41 160	69 500	21 000
Poisson’s ratio	0.3	0.33	0.33	0.15
Tensile yield strength, MPa (kgf/mm2)	205 (20.9)	137.3 (14)	147 (15)	–
Ultimate strength, MPa (kgf/mm2)	333 (34)	245.25 (25)	294 (30)	300 (30.6)

Physical-mechanical characteristics of used materials

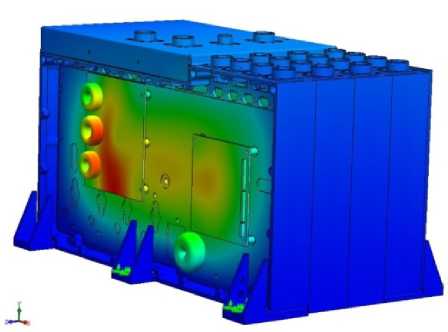
Fig. 4. First form of oscillations of model AB on frequency of 286 Hz

Рис. 4. Первая форма колебаний модели БА на частоте 286 Гц

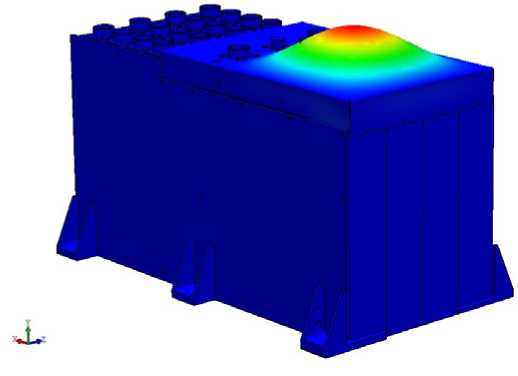
Fig. 5. Second form of oscillations of model AB on frequency of 316 Hz

Рис. 5. Вторая форма колебаний модели БА на частоте 316 Гц

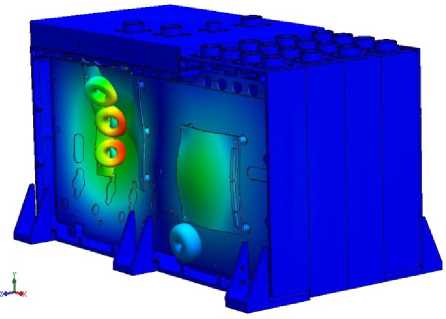
Fig. 6. Third form of oscillations of model AB on frequency of 362 Hz

Рис. 6. Третья форма колебаний модели БА на частоте 362 Гц

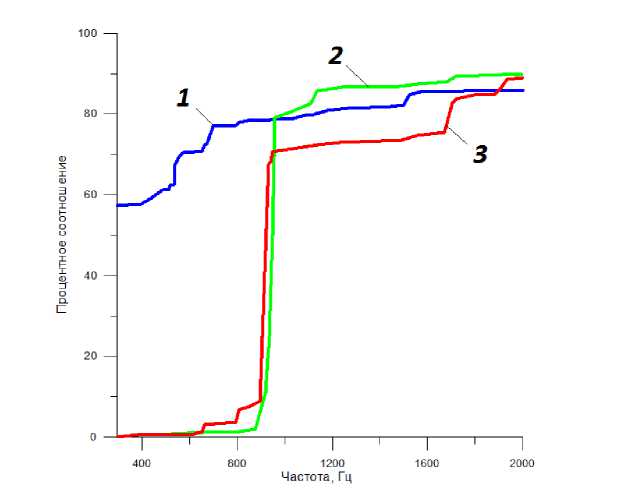
Fig. 7. Result factor of mass participation:

1 – mass participation in a direction of OZ axis; 2 – mass participation in a direction of OY axis; 3 – mass participation in a direction of OX axis

Рис. 7. Результирующий коэффициент массового участия: 1 – массовое участие в направлении оси OZ ; 2 – массовое участие в направлении оси OY ; 3 – массовое участие в направлении оси OX

Values of maximum stress and displacements OX , OY , OZ axes at quasi-static load

The load factor of η elements of the AB model is calculated by the formula

η = ^{σ b}    ≥ 1,                  (1)

^σ von Mises

where σ b is the yield strength of the material, MPa; σ von Mises is the calculated value of the stress according to Mises, MPa.

For principal stresses σ1, σ2, σ3, the Mises stress is expressed as

Table 2

Direction of effect	The maximum stress, MPa	The maximum displacement, mm
Along OX axis	9.7	0.012
Along OY axis	7.3	0.063
Along OZ axis	15.9	0.072

• =    (О1 - О2 )2 + (О2 -Оз )2 + (О1 -Оз )2

• ^О    von Mises     у                      2                       ^.

The minimum load factor in the base of the TCC along the OZ axis is n = 8-6 -

Stress and displacement distributions in the AB model under the effect of quasi-static accelerations along three mutually perpendicular axes are obtained (fig. 8–13). The maximum stress along the OZ axis occurs at the base of the TCC.

Modelling of the effect of random vibration. Border conditions:

• –    all elements of the model have a global contact with one another;

• –    damping in the model is 2 % of the critical;

• –    type of material model – linear, elastic, isotropic;

• –    the device is rigidly fixed over the entire surface of the mounting feet;

– the impact is applied to the base of the AB model consecutively in each of the three mutually perpendicular directions.

The maximum stress occurs at the base of the TCC at random vibration in the direction of the OX axis (tab. 3). The values of the maximum stress, accelerations and displacements at the level σ under the effect along each of the three mutually perpendicular directions are obtained.

The damping factor with respect to the critical damping was assumed to be 0.02. The finite element model of the device is presented in Section 2.

The minimum load factor in the base of the TCC along the OZ axis at the level 3σ, calculated by the formula (1), is η = 1.39.

Forms and values of accelerations, displacements and stress in the AB model at the effect of random vibration in the direction of the axes in accordance with tab. 3 are shown in fig. 14–22. In some drawings several elements of the design are hidden for the better visualization of maximum accelerations, displacements and stress.

Fig. 8. Distribution of stress in AB model at quasi-static load along OX axis

Рис. 8. Распределение напряжений в модели БА при квазистатическом воздействии по оси ОХ

Fig. 9. Distribution of stress in AB model at quasi-static load along OY axis

Fig. 10. Distribution of stress in AB model at quasi-static load along OZ axis

Рис. 10. Распределение напряжений в модели БА при квазистатическом воздействии по оси ОZ

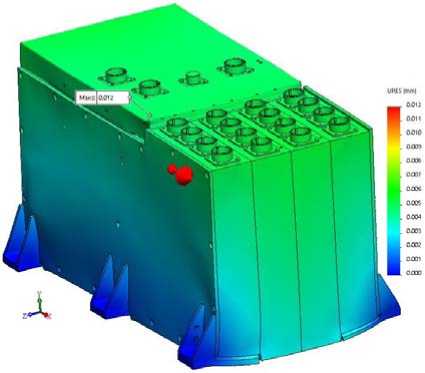
Fig. 11. Distribution of displacement in AB model at quasi-static load along OX axis

Рис. 11. Распределение перемещений в модели БА при квазистатическом воздействии по оси ОХ

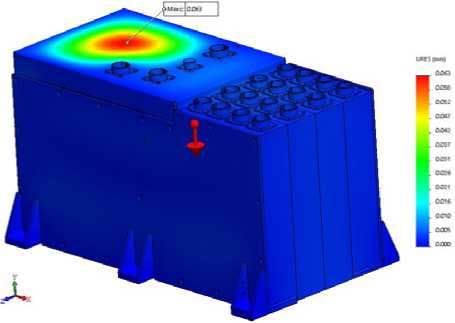
Fig. 12. Distribution of displacement in AB model at quasi-static load along OY axis

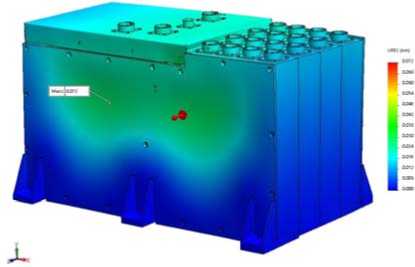
Fig. 13. Distribution of displacement in AB model at quasi-static load along OZ axis

Рис. 13. Распределение перемещений в модели БА при квазистатическом воздействии по оси ОZ

Table 3

Values of maximum stress, displacements and accelerations along OX , OY , OZ axes at effect of random vibration

Direction of impact	The maximum stress, MPa	The maximum displacement, mm	The maximum acceleration, g
Along OX axis	29.8	0.006	10.98
Along OY axis	5.66	0.177	72.09
Along OZ axis	32.9	0.135	56.05

Fig. 14. Distribution of accelerations in AB model at effect of random vibration along OX axis

Рис. 14. Распределение ускорений в модели БА при воздействии случайной вибрации по оси ОХ

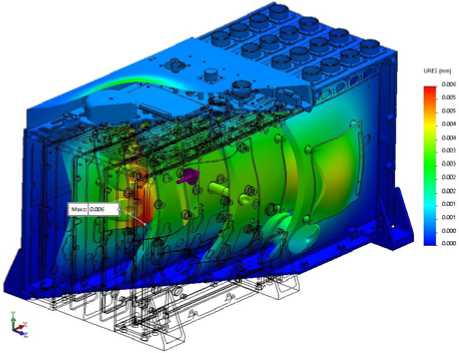
Fig. 15. Distribution of displacements in AB model at effect of random vibration along OX axis

Fig. 16. Distribution of the stress in AB model at effect of random vibration along OX axis

Рис. 16. Распределение напряжений в модели БА при воздействии случайной вибрации по оси ОХ

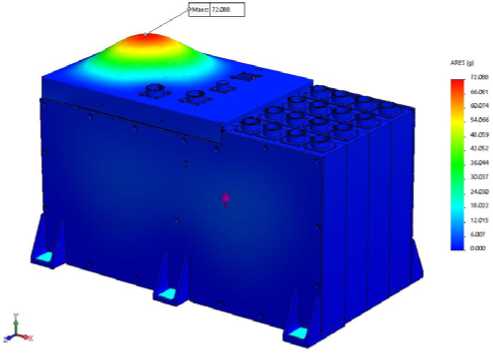
Fig. 17. Distribution of accelerations in AB model at effect of random vibration along ОY axis

Рис. 17. Распределение ускорений в модели БА при воздействии случайной вибрации по оси ОY

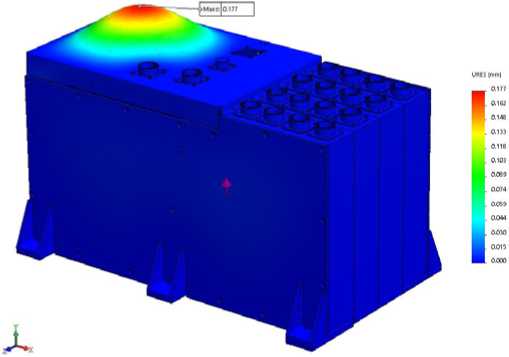
Fig. 18. Distribution of displacements in AB model at effect of random vibration along ОY axis

Fig. 19. Distribution of the stress in AB model at effect of random vibration along ОY axis

Рис. 19. Распределение напряжений в модели БА при воздействии случайной вибрации по оси ОY

Fig. 20. Distribution of accelerations in AB model at effect of random vibration along ОZ axis

Рис. 20. Распределение ускорений в модели БА при воздействии случайной вибрации по оси ОZ

Fig. 21. Distribution of displacements in AB model at effect of random vibration along ОZ axis

Fig. 22. Distribution of stress in AB model at effect of random vibration along ОZ axis

Рис. 22. Распределение напряжений в модели БА при воздействии случайной вибрации по оси ОZ

To predict the fatigue strength of the AB at given levels of effect of broadband random vibration, the predicted service life of the device can be determined from the formula

Т =------В-----,                   (2)

F0(σ/σД)m where ТВ is the number of loading cycles; F0 is the lower resonance frequency of the structure, Hz; σ is the maximum stress at the effect of broadband random vibration, MPa; σД is the fatigue strength endurance of the material, MPa; m is the index of the slope of the fatigue curve of the material.

For the bases of the TCC, the following parameters [16] were applied in the calculation: Т _В = 1 - 10 7 s; F 0 = 286.6 Hz; m = 9.55. Steel MA2-1 has the following characteristics: σ = 32.915 MPa; σ Д = 100 MPa.

Substituting the values of the parameters in formula (2), we get the predicted service life of the device Т = 1.4 - 10 9 s.

Modelling of the shock action. Modelling of the shock action on the AB, given in the form of an amplitude-frequency spectrum according to tab. 4, is carried out separately along each of the three mutually perpendicular axes: OX , OY , OZ (fig. 23–31).

Border conditions:

• –    all elements of the model have a global contact with one another;

• –    damping in the model is 2 % of the critical;

• –    type of material model – linear, elastic, isotropic;

• –    the device is rigidly fixed over the entire surface of the base;

• –    the impact in the form of a frequency spectrum is applied to the base of the AB consecutively in each of the three mutually perpendicular directions.

The maximum stress at the effect on the OZ axis occurs at the base of the TCC.

The most loaded element of the AB model is the base of the TCC at shock action along the OZ axis. The load factor of the side plate is n = 1.25.

Conclusion. The results of the analysis showed the following:

• –    the calculated minimum eigenfrequency of the AB model is f 01 = 286.6 Hz, which meets the requirements of the technical specifications;

• –    the minimum load factor at quasi-static action and sinusoidal vibration is 8.64 in the direction of the OZ axis;

• –    the minimum load factor at random vibration is 1.39 in the direction of the OZ axis;

• –    the maximum accelerations at random vibration along the OX , OY , OZ axes at the level of 3σ are 32.94g, 216.27g and 168.14g respectively;

• –    the minimum load factor at shock action along the OZ axis is 1.25;

• –    the maximum displacements at shock action along the OX , OY , OZ axes are 0.213, 0.56 and 0.76 mm respectively;

• –    the maximum accelerations at shock action along the OX , OY , OZ axes are 158.51g, 247.53g and 297.55g respectively.

The most critical types of loading are impact in the direction of the OZ axis and the impact of random vibration in the direction of the OZ axis. At the same time, the load factor in the base of the TCC is 1.25 and 1.39 respectively.

Based on the results of the analysis, locations for the installation of vibration-survey converters have been determined to measure the changes in the amplitude-frequency characteristics of the AB before and after the dynamic effects. When carrying out mechanical tests, the vibration-survey converters are installed on the side cover of the TCC, on the side of the base of the TCC located in the middle of the device (fig. 32), and on the upper part of the base of the TCC between the connectors at points 1 , 2 and 3 .

Thus, the analysis has shown that the design of the AB model meets the requirements of the technical specifications for resistance to external mechanical effects.

Table 4

Direction of impact	The maximum stress, MPa	Safety factor, η	The maximum displacement, mm	The maximum acceleration, g
Along OX axis	29.222	4.7	0.213	158.512
Along OY axis	79.083	1.74	0.555	247.531
Along OZ axis	109.84	1.25	0.758	297.549

Values of maximum stress, displacements and accelerations along OX , OY , OZ axes at shock action

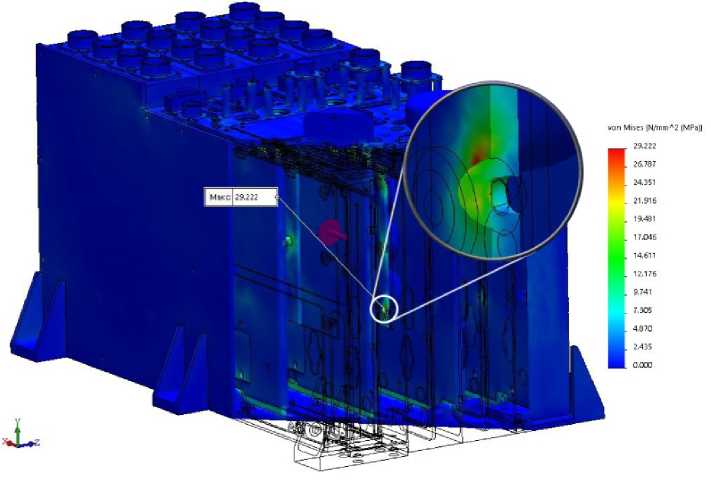
Fig. 23. Distribution of stress in AB model at shock action along OX axis

Рис. 23. Распределение напряжений в модели БА при ударном воздействии по оси OX

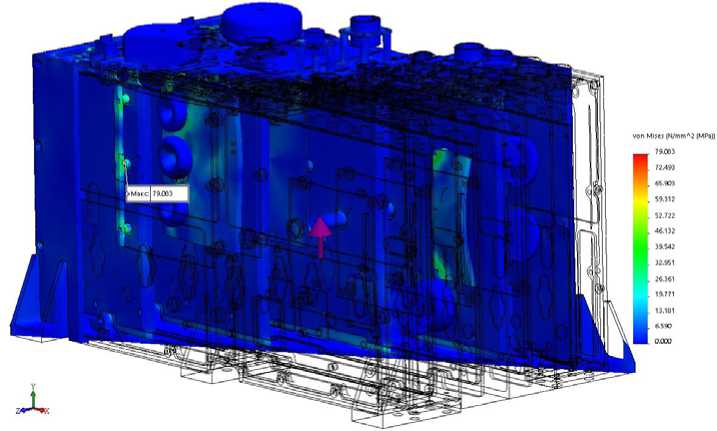
Fig. 24. Distribution of stress in AB model at shock action along OY axis

Fig. 25. Distribution of stress in AB model at shock action along OZ axis

Рис. 25. Распределение напряжений в модели БА при ударном воздействии по оси OZ

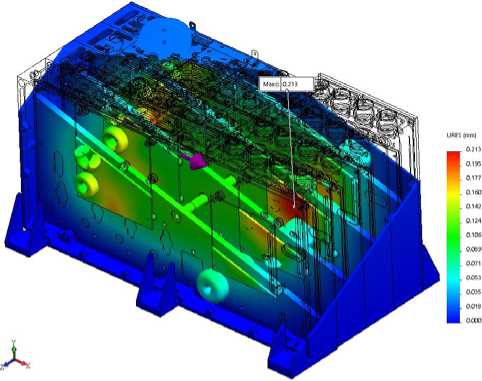
Fig. 26. Distribution of displacements in AB model at shock action along OX axis

Рис. 26. Распределение перемещений в модели БА при ударном воздействии по оси OX

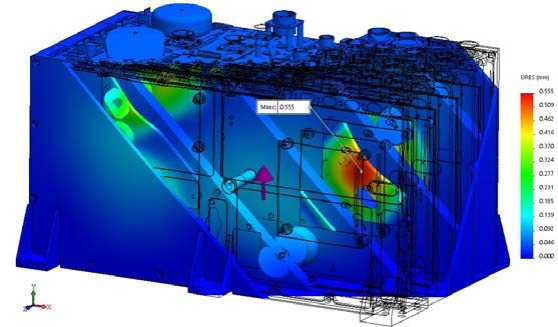
Fig. 27. Distribution of displacements in AB model at shock action along OY axis

Fig. 28. Distribution of displacements in AB model at shock action along OZ axis

Рис. 28. Распределение перемещений в модели БА при ударном воздействии по оси OZ

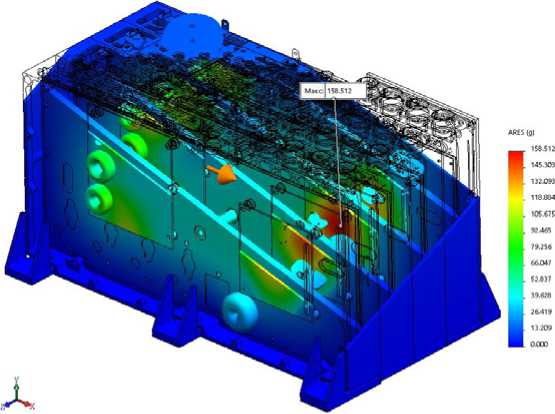
Fig. 29. Distribution of accelerations in AB model at shock action along OX axis

Рис. 29. Распределение ускорений в модели БА при ударном воздействии по оси OX

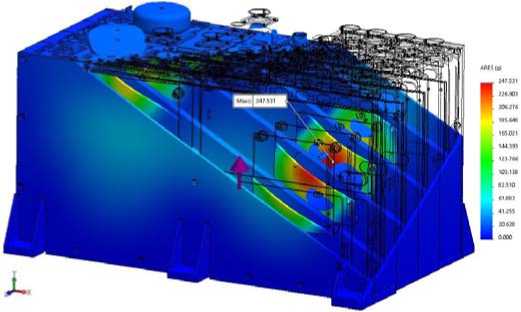
Fig. 30. Distribution of accelerations in AB model at shock action along OY axis

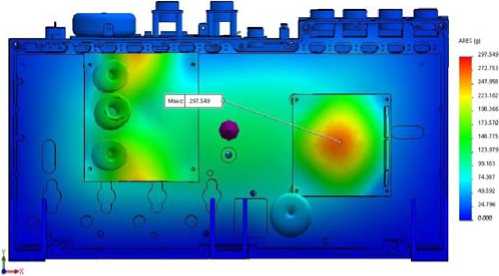
Fig. 31. Distribution of accelerations in AB model at shock action along OZ axis

Рис. 31. Распределение ускорений в модели БА при ударном воздействии по оси OZ

Fig. 32. Installation location of vibration-survey converters on AB

Рис. 32. Места установки виброизмерительных преобразователей на БА