Time deviations of physical properties of natural minerals

Physical properties at natural minerals sometimes can change in due course, and the sample thus can not be exposed to what – that to external influence and to be in rather stable thermodynamic conditions. If the mineral was in contact to an atmosphere this effect usually speaks influence of an atmosphere, however not all these changes can be explained by atmospheric influence? Such changes can take place even when atmospheric influence can be excluded (in vacuum or in depth dense layers of breed). The reason of this phenomenon – in influence on physical properties of a mineral of dot defects (for example, cationic vacancies).

Magnetic properties of minerals are in direct dependence on a direction of spin on units of magnetic under-lattices. The direction a back depends on size of a local magnetic field. Presence in crystal structure of dot defects can influence essentially size of a local magnetic field, so and on a direction a back. As spontaneous redistribution of dot defects, hence, probably and change of magnetic properties in due course is possible in due course [1-3].

The purpose of work : to give an explanation change of physical properties of minerals in due course

Inversion of the spin at a various configuration of defects in the second coordination sphere

Let’s show it by the example of structure such as NiAs (Fig. 1 b) with various distributions of cationic vacancies in structure. Let in this system ferromagnetic spin ordering in basic planes and antiferromagnetic between planes is carried out. Magnetic properties of system can be described Heisenberg Hamiltonian

H = -Z IfmSfSm, jm where f, m – units of a crystal lattice; Ifm – exchange parameters; Sf – the operator of the spin on unit f.

Though generally exchange interaction can be long-range and oscillatory (mechanism RKKI), we shall be limited to consideration of a case when I_fm are distinct from zero only for the nearest neighbours. In the elementary case exchange parameters accept only two values: I 22 between basic planes and I₁₁ – inside a plane.

If to be limited to a case of consideration Ising parts Hamiltonian

H = -£ Im 6f 6m, fm

(where 6 ₍ = 2 S xx ), own values partial own functions ff

I♦- ("» = |ПГ)„П^,

I „ I

Therefore own values energy W n possible to write down as:

W = - 4 S I m К n ⁶ f ⁶ m ^ф . ) = ^- 4 S ¹ m ⁶ '? ) ^{6 m}') .

From a condition of a minimum of energy W =min( W ) it is received 0 n

W 0 -- 4 s - ⁰ ,= 0 , where

S, =Z Ifm^,. m it is local field on unit f.

Thus, a necessary condition of minimum W0 is < 7 0 e 0 >  0, from which follows, that the direction for the spin is unequivocally connected with is familiar a local field

• - 0 = sign s 0 .

For example, if ε f =0, spin in unit f is «paramagnetic» and can have any orientation. Inclusion of a small magnetic field along an axis of quantization removes this degeneration and spin accepts value ^CT 0 = 1.

Within the framework of considered model there is a final number of types of the local fields described by various type of distribution of vacancies around of the given unit f. For crystal structure such as NiAs the basic condition the back on unit f, not containing vacancy in the nearest environment, 00 s I e

S 0 = ⁶ 1 11 — ² I 22 <  ⁰-

If in a basic plane in which there is a cons idered unit f, there are vacancies the basic condition will depend on their number, however the sign on a local field thus will not vary:

^ 0 = 5 I ii — 2 I 22 <  0,

^ 0 =- 2 1 22 <  0,

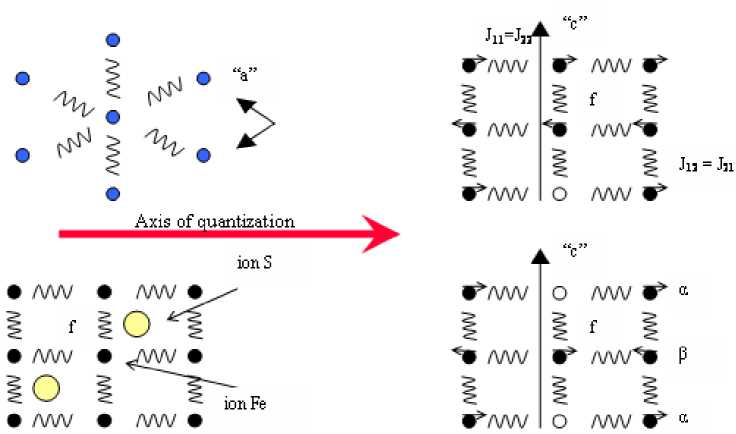
Fig. 1. Crystal structure type of NiAs with the various maintenance (contents) of vacancies of cations

• I .e. s 0 consistently accepts values for 1, 2, ...., 6 vacancies in the nearest environment. For definiteness, the magnetic structure submitted on Fig. 1 with is considered. An axis of quantization – X.

If vacancies are in the next basic planes the local field on unit f can accept both positive and negative value. Even if to accept, that i.e. presence of one vacancy does not result in change of a sign 0

at a local field 61ц<122 on unit f £f (Fig. 1c) two vacancies located in planes a, inevitably should cause reorientation a back (Fig. 1в) [4-7]. The basic condition for the first case will look like s0 = 61 -1 < 0

and for the second –

4 - 6 ;„

If the unit f is surrounded with vacancies and in a plane α, and in a plane β spins will be in this case in a «paramagnetic» condition.

Concept and principle of calculation of energy of cationic vacancies

For calculation of energy of dot defects of any kind it is necessary to write down Hamiltonian which should take into account all processes in which these defects participate. Own values of it Hamiltonian also will be set of the resolved power levels which can borrow dot defects.

That the role of defects was enough appreciable, their concentration in structure should be concerning big. It is the best way to lead the mathematical analysis by the example of any stoichiometric connection, for example, a pyrrhotite in which structure there are cationic vacancies [5-7].

Hamiltonian conditions of vacancies in stoichiometric connections of type can be presented a pyrrhotite as:

H = Z * f a>y + Z B fm a f a f + Z V f^m + Z ( ^ ^⁺+ + Ф a f ) f                 f , m                 fm                  f

Where af (af) the operator of a birth (destruction) of vacancy in f unit of a crystal lattice, nf = a+aj - the operator of number of vacancies in f an ohm unit, Bfm, - integral of carry of vacancies between units f and m, V – potential of interaction of vacancies, races put in units f and m, φ – f m amplitude of probability formation in crystal structure of defect on Frenkel.

The physical sense of the first sum in Hamiltonian can be understood from the following reasons. Hamiltonian magnetic interaction for stoichiometric connection it is possible to write down kind:

H — - V rec 2m fm f

If in crystal structure there are vacancies of magnetic cations, Hamiltonian magnetic interaction signs the following kind:

H j-pAp-S- pf = 1 it there is no vacancy in unit f, pf = 0 if there is a vacancy in unit f, Ifm integral of exchange interaction, Sf – the operator of the spin in f u^nit of a crystal lattice.

From the formulas submitted above follows, that at change of concentration of vacancies in a firm body his magnetic energy will change. If in a crystal there are no vacancies energy of magnetic interaction of some ion of the iron located in unit f, will be equal:

A e 0 = S x X I f S = e f .

jm

If in this unit f vacancy energy of magnetic interaction will change on size was formed (the axis X coincides with a direction a spin in crystal structure.) It is necessary to note, that the size ε f generally should depend on unit f. since in the nearest environment new vacancy in turn can be formed. It will be shown below, that at the account of interaction between vacancies the size ε_f practically will not depend on number of unit. Thus, ε f own values of the operator of potential energy of the vacancies, numerically equal energy necessary for destruction of magnetic interaction in f unit of crystal structure.

The second sum in Hamiltonian describes processes of moving of vacancies in the structure. It is obvious, that formed in some unit of a crystallographic plane vacancy can change the position as a result of processes next cation jump in the given vacant position.

Now we shall find out physical sense of the third sum to the very first formula Hamiltonian. The crystal structure of any stoichiometric connection is steady up to the certain number of vacancies in individual volume. We shall designate N 0 – limiting number of vacancies in some volume V 0 of substance. At N₁> N₀ this volume of substance is reconstructed in new structure, i.e. there is a single transition. It is natural to assume, that в connection there cannot be a local phase transition if the chosen volume V₀ is small enough (for example if have chosen one elementary cell). From here follows, that energy of transition of some volume V 0 in new structure should surpass energy of pushing out of superfluous vacancy, if in the neighbor it volume V₁ number of vacancies less critical. Thus, if as a result of fluctuation in the next volume V 1 of substance N 0, and in the given volume N> N0, vacancies diffuse in the next volume V₁.

The fact, that vacancies «feel» presence of other vacancies in elementary volume, V 0 at N> N 0 allows to enter interaction between vacancies, having simulated definitely potential of this interaction. It is obvious, that this potential gets out of structural features of concrete not stoichiometric connection.

Fourth (last) sum in Hamiltonian (H) describes processes of formation (destructions) of the vacancies caused by transition of cations from planes in interstitial space (or back), i.e. usual defects on Frenkel which probability of formation grows with increase in temperature of a crystal. At downturn of temperature of a firm body the ions located in interstice, with the greater probability take again vacant positions, than pass in interstice from units of lattice new cations. In case of constant thermodynamic parameters processes of formation and destruction of vacancies occur equiprobably.

Condition of splitting of single levels of cationic va cancies in a power zone

It is possible to show, that the account of moving of vacancies in structure results in splitting initial levels of energy ε f in some power zone.

Let’s write down Hamiltonian H only as two sums:

H 0 = Z = f a >f + Z B fm aa . f                      f , m

After transformation Fourier af = ( XZ e ak N k ,

Hamiltonian H 0 signs the following kind:

H о =]E \ (1

N x £ _e p - k ) f ) + (1 N x £ B^ fk - pm a + a p ^f                            ff • m)

Let’s make replacement εf average value as follows:

1 N

£ =   / £ f = £ о B = £ oV

N f N

Where ν – concentration of vacancies in a plane, N-number of units in a plane, NB – number of vacancies in a plane. Similar averaging of energy ε means the assumption of an equiprobable

f arrangement of vacancies in all units’ f crystal structure.

For transformation of the second expression to parentheses in the formula we shall take advantage of the following designations: m=f+h в (h )= 1n-l^BfJ . h

Finally Hamiltonian H0 it is possible to present as:

Hо =^{5 + B(k)} akak k

From last formula follows, that the single power level ε f is split at the account of movement of vacancies in some zone, which width B (к).

Inversion a back – result of transition of vacancy on extrinsic a level

It is obvious, that vacancies are distributed on the resolved power levels within the limits of a zone, however vacancies, induced process revolution a spin appear below power zone, i.e. on foreign a level near to a bottom of a zone.

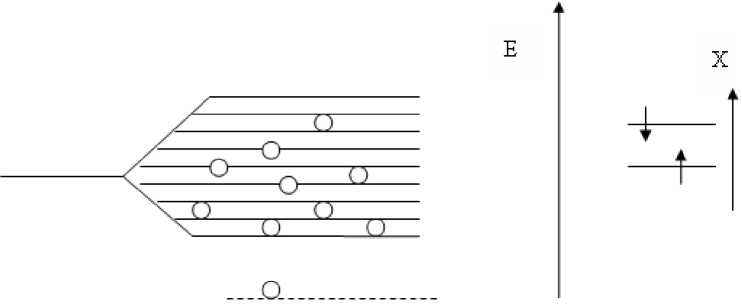
Fig. 2. Power levels of cationic vacancies

Really, the spin after inversion, passes, apparently from Fig. 1 in a condition with smaller energy since his orientation coincides with an axis of quantization. However this condition is possible only at presence in the nearest environment of the cationic vacancy responsible for this inversion. Leaving of vacancy from the given position would be accompanied by increase in energy of cation; therefore she is stabilized in this condition. This condition energetically lowers, than a similar condition of vacancy close cation with no inverting spin. Thus inverting the back on unit near to vacancy translates her on foreign a level with formation of pair «Vacancy – cation».

Generally parity between exchange integrals can be others, and the configuration of cationic vacancies in the second coordination sphere, the surrounding given unit of crystal structure, can be other. Vacancies can be in even and odd basic planes and accordingly the total magnetic moment of under-lattices (and in a result and the magnetic moment of a mineral) can or grow or decrease, depending on a concrete case.

In the conclusion it is possible to draw conclusions:

• 1.    The opportunity of inverting spin, induced is proved to dot defects;

• 2.    The opportunity of formation in structure of steady pairs «vacancy – cation», minerals influencing magnetic properties is shown.

• 3.    The opportunity is proved at enough high concentration of defects (the stoichiometric connections possessing the distant magnetic order) magnetic properties of minerals can change eventually without thermodynamic, chemical, radiating, atmospheric or other external influence.