Типизация неправильных пространственных разбиений

Размещения разнотипных случайных точек в 2D, 3D и многомерных пространствах с точки зрения «тяготения или отталкивания» имеют отношение к целому ряду дисциплин и требуют для анализа синтетического метода. Так, для проверки «тяготения» точек двух типов (б и ч) в работе Ю. А. Ткачева [15] использован частотный анализ «сочетаний типов ближайших точек». Компьютерным моделированием установлено, что границей «тяготения» и «отталкивания» является соотношение сочетаний (бб, чч, бч), отвечающее независимым случайным распределениям точек разных типов. Оба аспекта — метод ближайших точек и проблема равновесия противоположных тенденций — вызывают ассоциации из разных дисциплин, которые рассматриваются и обобщаются в этой статье. Логика рассуждения следующая. Вначале от точек совершается переход к разбиению пространства по Вороному — Дирихле и вслед за этим к более широкому классу разбиений, сохраняющих те же контакты полигонов (полиэдров, политопов — здесь и далее). Затем обсуждается задача определения границ между тенденциями «тяготения» и «отталкивания» разнотипных полигонов. В разных терминах она имеет место в химии, популяционной биологии, генетике и лучше всего разрешается в виде бинарных равновесий Харди — Вайнберга. Применительно к типизации петрографических структур (это основной акцент статьи) они обобщены на тернарные и куотернарные контакты минеральных зёрен. По сути, равновесия Харди — Вайнберга (и их обобщения) задают классифика- ционные границы между разбиениями, отличающиеся от «равновесных». Возникает задача их типизации, решаемая с помощью алгебраических квадратичных и отчасти кубических форм. К одному типу отнесены разбиения, обладающие топологически эквивалентными структурными индикатрисами.

Разбиения

Метод «ближайших точек» наводит на мысль о разбиении пространства по Вороному — Дирихле, которое порождается любой точечной (r, К)-системой Делоне [2, с. 60—62, 158—160; 6, с. 40—49]. На рис. 1 разбиение показано на примере простейшей К-модели (модели Колмогорова) кристаллизации горной породы с постоянными скоростями роста кристаллов, обусловившими прямолинейность межзерновых границ [1]. Применительно к нашим задачам процедура преобразует анализ «ближайших точек» в анализ «ближайших окружений» полигонов. Фундаментальное свойство разбиений Вороного — Дирихле хорошо известно: все точки полигона располагаются ближе к порождающей его точке, чем к любой другой такой точке. Реже отмечается, что при случайном расположении точек соответствующие им полигоны (в 2D) контактируют по 3, полиэдры (в 3D) — по 4 в одной точке. Геометрическая вероятность иного исхода равна нулю [7]. Уже в 2D это позволяет получить интересный результат.

Границы полигонов Вороного — Дирихле образуют граф. Пусть N0 — число его вершин (точек схождения по- лигонов), N1 — рёбер (границ полигонов), N2 — самих полигонов. Средняя координация полигона равна 2N1/N2, так как каждое ребро принадлежит двум полигонам. По теореме Эйлера:

N o - N i + N 2 = 2.

Но 3N₀ = 2N i , так как из каждой вершины выходят три ребра, а каждое из них принадлежит двум полигонам. Из совместного рассмотрения соотношений получаем:

2N1 / N2 = 6 (1 - 2 / N2) ^ 6 при V >/.

Как инвариант полигонального разбиения среди природных объектов лишь в пчелиных сотах 6 достигается строгим построением, все клетки — гексагоны, разбиение правильное. В иных весьма разнообразных неправильных разбиениях (рис. 2, «точками» являются центры кристаллизации, контракции и т. д.) 6 достигается в среднем в результате компенсации более высоких и низких координаций, с теми или иными моментами статистического распределения. Они могут быть рассчитаны и, по-видимому, содержат информацию о генезисе полигональной (полиэдрической) структуры. Несколько более сложное рассуждение можно провести и для 3D-разбиений [17, 19].

Таким образом, имеет смысл характеризовать и сравнивать пространственные распределения точек (каждого типа раздельно и всей системы в целом) параметрами (среднее, дисперсия, асимметрия, эксцесс) статистических распределений координаций полигонов. Трудности, возникающие на этом пути в 3D, очевидны и относятся к технической стороне проблемы. Например, как найти статистику контактов минеральных зёрен в горной породе (по 4 в точке), если по законам геометрических вероятностей они не попадают в плоскость сечения? Это именно тот случай, когда решение теоретической проблемы подразумевает техническую подоплёку. (Исторический пример: фундаментальная теория Фёдорова — Шёнфлиса нашла практическое применение лишь после открытий Лауэ и Брэггов.)

Равновесия

Задача определения границ между тенденциями «тяготения» и «отталкивания» в разных формах возникала в естественных науках как частный случай проблемы классификации [12, 13]. Удивительным образом, несмотря на специфику, во всех частных решениях прослеживается сходная логика — анализ взаимодействий (контактов, столкновений, встреч...) агентов.

Химия. При динамическом равновесии обратимой химической реакции mA + nB = pC + qD скорости прямой и обратной реакций равны:

k1 [A]m [B]n = k2 [C]p [D]q, где k1 и k2 — константы прямой и обратной реакций [8]. Для нашего рассмотрения важно, что равновесие определяется через произведения концентраций реагирующих веществ. Чем они выше, тем чаще столкновения молекул в каждой единице объёма.

Биология. Модель эволюции популяций типа «хищник — жертва» имеет вид:

dx / dt = a x — в x y , dy / dt = — у y + 3 x y , где x и y — число травоядных и плотоядных; а, в, у, 3 > 0 — параметры модели [5, 16, 18]. Уравнения прироста травоядных (при отсутствии хищников) и убыли плотоядных

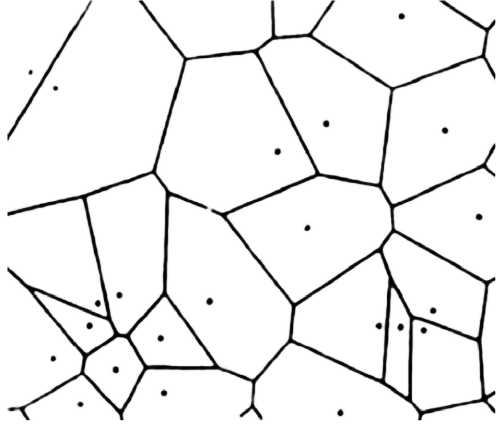
Рис. 1. (r, R)-система Делоне и соответствующее разбиение Вороного — Дирихле

Fig. 1. The Delaunay (r, R)-system and related Voronoy — Dirichlet tiling

Рис. 2. Полигональные разбиения поверхностей в природе: пчелиные соты, снежник (фото автора), такыр, солончак, петрографический шлиф, базальтовая отдельность, современные и ископаемые кораллы (фото из Интернета)

Fig. 2. Polygonal tilings of the surfaces in the nature: honeycomb, snowfield (authorsphoto), takyr, salt marsh, petrographic thin section, basaltic parting, modern and fossil corals. I-net, unless otherwise specified

(при отсутствии жертв) связаны через произведение x • у, пропорциональное числу встреч, влекущих убыль жертв и прирост хищников в ареале обитания.

Генетика. Английский математик Дж. X. Харди и немецкий врач В. Вайнберг независимо получили формулу, описывающую равновесие генотипов в потомстве [9, с. 362—368; 10, с. 126—128]. Если р и q — частоты (вероятности) конкурирующих генов А и В (в условной записи рА + qB = 1), то равновесные частоты генотипов АА, АВ (то же, что ВА) и ВВ среди потомков могут быть рассчитаны по формуле:

(рА + qB)2 = p2 AA + 2pq AB + q2 BB = 1.

Отклонения от равновесных частот указывают на генетический дрейф — результат естественного или искусственного отбора. В самом общем смысле формула Харди — Вайнберга характеризует идеальное перемешивание двух сочетаемых (сталкивающихся, конкурирующих, контактирующих^) разнородных сущностей, что роднит приведенные примеры. Она обобщается по числу слагаемых:

(P 1 A 1 + — + P n A n )² = 2 P ij A i A j = 1, где i, j = 1, —, n.

Типизация

Анализ противоположных тенденций с точки зрения равновесий Харди — Вайнберга содержит любопытный методологический нюанс. Представим, что статистический критерий (например, х²) показал на требуемом уровне значимости согласие эмпирических и теоретических вероятностей P ij (P ij _k, P ijki ). (Автором получено такое согласие для бинарных и тернарных межзерновых контактов в нескольких шлифах двуполевошпатовых среднезернистых гранитов.) Естественное стремление исследователя — интерпретировать установленное равновесие в категориях термодинамики или естественного отбора в зависимости от специфики системы. Но в самой ситуации не всё так просто. Ведь для природных систем равновесие Харди — Вайнберга представляет классификационную границу, на которую попасть невозможно. Всякое состояние системы находится по ту или иную сторону от неё, в том или ином классе неравновесных состояний. Применительно к пространственным разбиениям эвристичное решение проблемы дают алгебраические квадратичные и кубические формы.

Квадратичные формы. Формула Харди — Вайнберга, обобщённая на произвольное число слагаемых, допускает двоякое рассмотрение. С одной стороны,

(P 1 A 1 + — + P n A n )² = 1, что равносильно p 1 A 1 + — + P n A n = ± 1.

Формально в фазовом пространстве (А 1 , —, A n ) равновесие Харди — Вайнберга выражается парой параллельных прямых (n = 2), плоскостей (n = 3) или гиперплоскостей (n > 3). С другой стороны, небольшое варьирование коэффициентов p i приводит к уравнению:

!у Pi AiAj = 1, где квадратичные формы уже не являются полными квадратами, но определяют структурные индикатрисы — поверхности центрального типа, так как точки (Ai, Aj) и (—Ai, —Aj) принадлежат им одновременно. Это эллипсы и гиперболы (эллипсоиды и гиперболоиды), легко распознаваемые приведением квадратичной формы к каноническому диагональному виду. Теория опубликована нами ранее [3, 4] и применима для типизации бинарных отно шений в разбиениях пространства на разнотипные полигоны. (Заметим, что среди индикатрис возможны лишь те, которые обладают ненулевым детерминантом. Поэтому невозможны цилиндры, хотя они и являются центральными поверхностями второго порядка.) Для горных пород структурные индикатрисы столь же информативны, сколь и оптические индикатрисы, характеризующие совокупный эффект взаимодействия света с кристаллом.

Для n = 2 поле вероятностей генотипов А 1 А 1 (рц = р 1 ²), А 1 А 2 (2р₁₂ = 2р 1 р₂) и А₂А₂ (р₂₂ = р₂²) удобно показать на барицентрической диаграмме (рис. 3, для удобства разнесена на три уровня), так как их сумма равна 1. Здесь равновесие Харди — Вайнберга — линия S₂³. Разделяемые ею области по конфигурации напоминают поля составов различных минеральных серий. И это позволяет усомниться в правильности прямолинейных границ между минеральными видами согласно «правилу 50 %». Здесь же можно показать эффект «непрерывного перехода» между структурными типами горных пород. Из одного класса в другой в поле диаграммы можно пройти по непрерывному пути 1—5. Но это не противоречит радикальной перестройке структуры в точке 3, отмечаемой изменением типа индикатрисы (эллипс в точках 1 и 2, гипербола в точках 4 и 5).

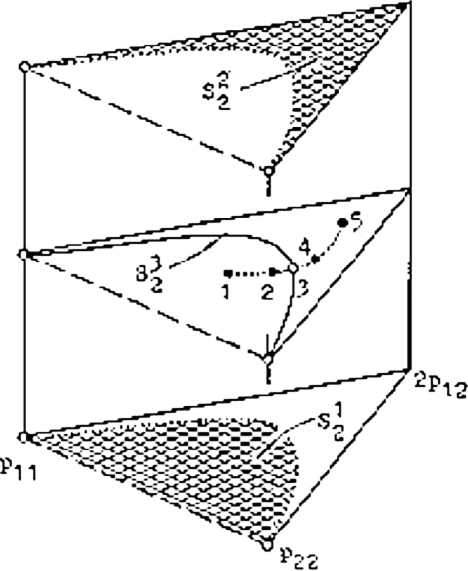
Рис. 3. Барицентрическая диаграмма (рц, 2р гг , р₂₂) для n = 2

Fig. 3. Barycentric diagram (рц, 2р₂₂, р₂₂) for n = 2

Кубические формы. Формула Харди — Вайнберга обобщается по степеням на тернарные:

(P 1 A 1 + — + P n A n )³ = 2 P ijk A i A j A k = 1, где i, j, k = 1, —, n и куотернарные отношения:

(P 1 A 1 + — + P n A n )⁴ = 2 Py ki A i A j A k A i = 1, где i, j, k, l = 1, —, n.

По-видимому, в генетике эти обобщения смысла не имеют. Иное дело — в петрографии. О технической труд- ности анализа куотернарных межзерновых контактов говорилось выше. Но анализ тернарных контактов в n-минеральных горных породах вполне может быть выполнен в шлифах, например, ради ответа на вопрос, отвечают ли массивные текстуры равновесию Харди — Вайнберга. При кажущейся очевидности ответа с этой точки зрения они ранее не изучались. В принципе, изучение петрографических структур следует выполнять в 3D. Анализ в 2D оправдывается лишь тем, что их классификация и номенклатура сформировались также по наблюдениям в 2D.

Для типизации тернарных отношений в разбиениях пространства на разнотипные полигоны можно использовать кубические формы, относя разбиения с топологически эквивалентными структурными индикатрисами к одному типу. Проблема состоит в том, что фундаментальная алгебраическая теория весьма сложна [11]. Для наших целей она может быть адаптирована при n = 2, то есть представлена в кубических кривых на плоскости благодаря их ньютоновой классификации [14]. Их разнообразие намного больше, чем для квадратичных кривых (рис. 4, из квадратичных кривых на плоскости в качестве индикатрис допустимы лишь эллипс и гипербола). Но остаётся вопрос, какие из них отвечают реальным системам, например статистикам тройных контактов зёрен в биминераль-ных горных породах. Повышение размерности пространства до n = 3, то есть изучение разнообразия кубических поверхностей, отвечающих статистикам тройных контактов зёрен в триминеральных горных породах, можно ожидать от методов компьютерной графики.

Заключение

Таким образом, проблема описания размещений разнотипных случайных точек в 2D, 3D и многомерных пространствах с точки зрения их «тяготения или отталкивания» есть во многих естественных науках. Она легко трансформируется в проблему описания соответствующих неправильных разбиений пространства, сохраняющих особенности разбиений по Вороному — Дирихле. (Так, в 3D два полиэдра граничат по поверхности, три — по ребру, четыре — в точке. Таково строение горных пород, металлов и сплавов.) Равновесия Харди — Вайнберга, обобщённые на тернарные и куотернарные межзерновые отношения, представляют собой классификационные границы в многообразии статистически неравновесных петрографических структур. Последние предложено типизировать по структурным индикатрисам — соответствующим поверхностям 2-го и 3-го порядков. К одному классу предложено относить структуры, обладающие индикатрисами одного топологического типа. Наличие теории алгебраических форм 3-го порядка лишь для двух переменных (ньютонова классификация плоских кривых) вынуждает ограничиться здесь лишь описанием биминеральных петрографических структур. В целом междисциплинарный подход к решению проблем представляется весьма продуктивным.

Автор благодарит рецензента, профессиональные замечания которого весьма способствовали улучшению статьи.