Типовые звенья в структурах виброзащитных систем и автоматического управления

Введение . В структурной теории виброзащитных систем широко используются структурные аналоги математических моделей в виде структурных схем эквивалентных в динамическом отношении систем автоматического управления (САУ) [1]. В теории автоматического управления, так же как и в структурах виброзащиты, используются типовые элементарные звенья. Передаточная функция САУ, имеющая вид произвольного полинома, может быть разложена на простые множители, т.е. представлена через передаточные функции звеньев.

При всей общности подходов построение дополнительных цепей, вводимых в структуру виброза-щитных систем, имеет свою специфику, что требует учета ряда особенностей.

• I.    Постановка задачи. Передаточная функция цепи дополнительной обратной связи в виброза-щитной системе определяется следующим образом:

  W don ( ^p )

  
  

  n

  a о + a i p + ... + a_np

  ^b 0 ⁺ b i ^{p +} ... ⁺ b m P m

  
  
  
  

где n,m - натуральные числа (n < m ); ai-, bi - коэффициенты, определяемые конструктивными особенностями ВЗС (i = 1, n; j = 1, m) [1]. В соответствии с (2) элементарные звенья ВЗС могут быть найдены путем упрощения Wдоп ( p) через «зануление» ai, bj в определенном порядке.

Возникающая проблема заключается в том, что нужно обозначить границы смывания двух подходов, определяемых в теории ВЗС и теории автоматического управления.

• II .    Сравнительный анализ . В теории автоматического управления (ТАУ) выбор типовых звеньев опирается в значительной мере на представления о некотором наборе типовых звеньев в силу традиции и связи с преобразованиями Лапласа:

k , p , - Tp ± 1, -—, T ² p ² ± 2 ^ Tp +1, —-------- .           (2)

P Tp ± 1                  T ² p ² ± 2 ^ Tp + 1

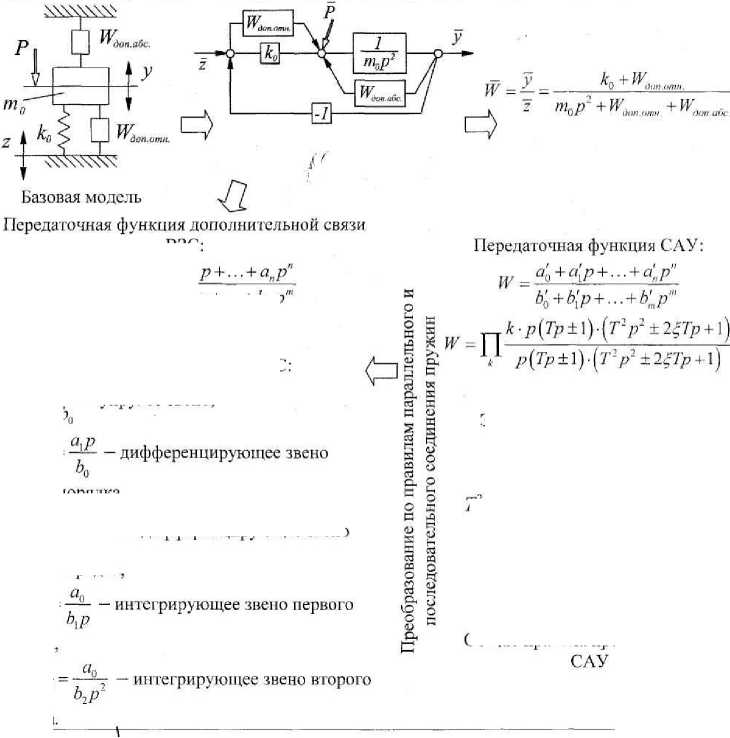
Напомним, что k в теории автоматического управления [2] называется передаточным коэффициентом, T - постоянной времени и ^(0 < ^ < 1) - коэффициентом демпфирования. С вышеприведенных позиций в понимании элементарных звеньев в (2) можно увидеть, что k, p, — являются элементарны- p ми, а остальные могут быть получены путем использования правил последовательных и параллельных соединений, как это принято в теории автоматического управления. Схема соотношения правил преобразования показана на рисунке 1. Хотелось бы отметить существенную особенность мехатроники ВЗС. Она связана с тем, что дополнительная связь, или дополнительная цепь, имеет размерность звена, на входе которого имеется смещение, а выходом является сила. То есть мы рассматриваем, по существу, механическую цепь, состоящую из однотипных элементов. Таких элементов пять, но к ним на таких же условиях может быть добавлено, при определенных условиях, звено чистого запаздывания. Такие элементы являются дуальными элементами и соединяются между собой для образования более сложных структур по правилам последовательного и параллельного сложения пружин [3].

Передаточная функция (1) в нашем случае относится к дополнительной механической цепи, вводимой определенным образом в структурную схему эквивалентной в динамическом отношении САУ. Сложность этой цепи предопределяет структуру, число элементарных звеньев и правила их коммутации.

W = Ар =

первого порядка,

Д^ = Ар1 = —™--дифференцирующее звено второго порядка.

р порядка, порядка.

Элементарные звенья С АУ:

Гр +2^Tp+V

Гр2 + 2^Тр + \

?(0

к, р, Тр+Х.

Р

’ Tprf 1

Рис. 1. Схема, поясняющая взаимосвязь между правилами преобразования в дополнительной цепи обратной связи и в структурной схеме САУ

ВЗС:

^Лр^^ ,

beAbtp*...+bmp

Элементарные звенья

№, = к = — — упругое звено, b

Общие правила преобразования

При рассмотрении САУ как таковой определяется передаточная функция ВЗС в целом, что приводит к выражению, имеющему в общем случае такой же тип, что и выражение (1). Но в двух случаях эти выражения при всей внешней схожести имеют разный физический смысл. Подчеркнем, что элементарная база ВЗС формируется в рамках дополнительной обратной связи [1]. В свою очередь, элементная база САУ формируется для всей системы в целом. Элементная база ВЗС состоит из дуальных элементов вполне определенной размерности - все элементы имеют вход - смещение и выход - силу, т.е. каждый элемент является элементарной пружиной, но со своими зависимостями от частоты и т.д. При рассмотрении передаточной функции САУ в целом и ВЗС в частности типовые элементы, предлагаемые в ТАУ, не несут в себе ограничений, которые налагаются в дуальных механических цепях [3]. В сложных механических колебательных систем определяются соответствующие передаточные функции и используются общеизвестные правила структурных преобразований. При формировании дополнительных обратных связей и дополнительных механических цепей в рамках структурной теории, составляющей основу ме-хатроники ВЗС [4], имеются некоторые особенности в правилах построения структур, что не противоречит законам механики и теории автоматического управления.

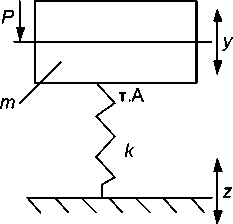
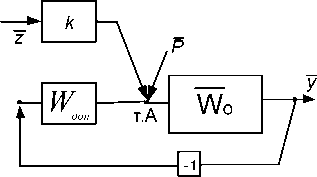
• III .    Общие методические положения о структурном подходе . Основой виброзащитной системы является механическая колебательная система. Ее простейшая форма - это объект массой ( т ) и упругий элемент ( к ) . Такую систему можно назвать базовой моделью. Ей соответствует эквивалентная в динамическом отношении система автоматического регулирования (рис. 2 а, б).

а)

б)

б

Рис. 2. Базовая модель ВЗС (а) и ее структурная схема (б)

Структурная схема дает представление о месте и роли упругого элемента, на вход которого подается смещение (у). Выходом звена с передаточной функцией Wgon = к является сила. Эта сила подает ся на вход второго звена с передаточной функцией W) =---— Такое звено в структурной схеме являет- mp2

ся «сумматором», поскольку на вход собираются все силы. Это звено выполняет базовую функцию и не входит в число элементарных звеньев и имеет по размерности другую передаточную функцию, так как выходным сигналом является смещение (у). В такой системе минимальной сложности звено Wgon = к создает силу упругого взаимодействия. С позиции теории автоматического управления (ТАУ) упомянутое звено называется усилительным. Второе базовое звено служит интегрирующим звеном второго порядка, которое упругую силу «трансформирует» в смещение. Обе схемы на рисунке 2 а, б соответствуют одному и тому же дифференциальному уравнению ту + ку = kz + P (t).                                  (3)

Структурная схема на рисунке 2 б – это графическая форма отображения дифференциального уравнения (3). Получение уравнения (3) может быть реализовано на основе принципа Даламбера или путем использования уравнения Лагранжа. Для нас важным обстоятельством является выбор в базовой модели «ключевого» элемента – это объект массой m . Точнее, «ключевым» элементом является материальная точка массой m , относительно которой составляется уравнение кинетостатики. Упругий элемент с коэффициентом жесткости k является таким образом элементарным звеном, а два звена с передаточными функциями W ₁ и W ₂ создают базовую модель минимальной сложности, при этом W ' = к входит в расширенный набор элементарных звеньев виброзащитных систем.

Отметим, что точка А (рис. 2 а ) переходит в точку суммирования сил (точка А по рис. 2 б ), что дает возможность находить динамическую реакцию через соответствующую передаточную функцию.

Усложнение ВЗС может идти через параллельное введение к упругому элементу дополнительной цепи, передаточная функция которой может быть представлена в виде дробно-рационального выражения вида (1).

Дополнительная цепь с передаточной функцией Wдоп(p) является дополнительной обратной связью, вводимой в структурную схему (рис. 2 б). В этом случае можно использовать известные в ТАУ принципы введения простейших технических средств. Если традиционный набор элементов, образующих ВЗС, состоит из массоинерционного звена, пружины и демпфера, то расширенный набор включает в себя звенья, имеющие передаточные функции интегрирующего звена первого рода, интегрирующих и дифференцирующих звеньев второго рода, звена чистого запаздывания (хотя такой перечень элементов, по-видимому, мог бы быть продолжен).

Будем полагать, что физическая или конструктивно-техническая форма реализации типовых звеньев осуществима на основе звеньев пассивной и активной природы. Последнее связано с использованием в ВЗС механизмов, приводимых в движение от внешних источников.

Характерным для развиваемого подхода является восприятие упомянутых типовых элементарных звеньев, однородными в том отношении, что все они имеют передаточную функцию, представляющую (в области преобразований Лапласа) отношение изображения сигнала на выходе к входному сигналу. При этом входной сигнал представляет собой смещение, а выходной - силу соответствующего вида. В этом смысле типовые элементарные звенья являются совместимыми, а их соединение определяется правилами параллельного и последовательного соединений как двух упругих элементов (или звеньев). На рисунке 3 показано соотношение традиционного и расширенного наборов.

Классический подход

W_np = к - упругий элемент или пружина

W d«n = bp - диссипативный или демпфирующий элемент

Развиваемы подход

W ₌ -массо-инерционный

W ин 2 mp

W™ = bp -Дифференцирующее звено первого порядка

W „ = к * пропорциональное звено пр

W_диф = LP ² -дифференцирующее звено второго порядка

W =

W ин 1

W ин

A

p

- инетегрирующее звено первого порядка

^ -интегрирующее звено p

W = Ар -ap -звено чистого vv зап e запаздывания

Рис. 3. Соотношение традиционного и расширенного подходов типовых элементов ВЗС

Поскольку типовые элементы являются однородными (в вышеприведенном значении), то из сочетания или комбинации двух различных элементов могут быть получены передаточные функции типовых элементов второго уровня, которые состоят из основных элементов с применением правил «параллельной и последовательной» сборки [4]. Хотя число комбинаций на основе соединения трех типовых элементов достаточно велико, однако это множество комбинаций должно быть уменьшено из-за учета свойства соединения элементов. Оно заключается в том, что параллельные и последовательные соединения одного типа (пружина с пружиной, диссипативное звено с диссипативным, дифференцирующее звено второго порядка с таким же звеном и т.д.) дают и в комбинационном виде звенья такого же типа.

• IV.    Особенности правил соединения звеньев ВЗС . Рассмотрим ряд примеров соединений не одного типа, а соединений элементов различных типов. Представим передаточные функции звеньев второго уровня, используя информацию о возможных комбинациях при последовательно-параллельном соединении между собой типовых элементов первого уровня (табл. 1).

Таким образом, комбинируя между собой последовательные и параллельные соединения типовых элементов из набора первого уровня, можно получить передаточные функции типовых элементов второго уровня. При этом передаточные функции всех типов элементов, за исключением типового элемента чистого запаздывания (и его соединений), могут быть получены из выражения (1), как частные случаи, путем «зануления» соответствующих коэффициентов в частотных уравнениях знаменателя и числителя передаточной функции (1) дополнительной связи общего вида. Что касается передаточной функции звена чистого запаздывания, то ее упрощение можно произвести путем разложения экспоненциальной функции в ряд, что позволяет ввести этот типовой элемент в число известных.

Дальнейшее наращивание сложности комбинационного построения приводит к понятию механической цепи, формирующейся из соединенных типовых элементарных звеньев на основе упомянутых правил структурных преобразований. Отметим, что взятая сама по себе дополнительная обратная связь достаточно рационально преобразуется в компактные структуры на основе двухполюсников, что было приведено в работах [3].

Таблица 1 Возможные виды типовых звеньев второго уровня

Виды звеньев	Параллельное соединение	Последовательное соединение	Примечания
W 1 = k , W2 = -p	W ' = k + -p	W" = k-p -p + k	W - демпфер, W" - форсирующее звено первого порядка
W 1 = k , W2 = Lp2	W ' = k + Lp2	w „ = _l2ppp_ Lp2 + k	W’ -fV форсирующие звено второго порядка W” форсирующие колебательное звено второго порядка
W 1 = k , W 2 = - p	w , = - + kp p	w » = -k - + kp	W’ - 4._____ .   . форсирующие интегральное звено первого порядка Wff - периодическое зве но
W = k , W 2 = 4 p	W ' = pk’-p	W"= -k 2 - + kp2	форсирующие интегральное звено второго порядка, колебательное звено
W 1 = k , W2 = Ae- a p	W' = k-e " ap	W" =__-k__ ke"ap + -
W 1 = bp , W2 = Lp2	W' = bp + Lp 2 = = p ( b + Lp )	W = bLpL Lp + b	форсирующие интегральное звено второго порядка
W 1 = bp , W2 = - p	W ' = - + bbp 2- p	w „ = - 2 bp bp2 + -	W" - „    „ _. „ „ колебательное звено с затуханием
2       A W = Lp 2, W 2 = - p	W ■= Lp 3+ - p	W- = -Lp2- Lp3 + -
W 1 = bp , W 2 = -e- ap	W '= bp + -e ~ ap	W" = bp-6 ap bp + -e ~ ap
A          9 W = — W 2 = Lp2 p	w=Lp 4 ± -p	W- = -Lp2- Lp 4 + -
W 1 = Lp2 , W 2 = -e - ap	W == Lp2 + -e - ap	W,, = Lp2-e a p Lp 2 + -e" ap
W i = -, W 2 = pp	w< = - i p + - -2 2 p	W "  =___ - 1 - 2___ p ( - 1 p + - 2 )
W 1 =    , W 2 = -e- ap p	w ' = - 2 + -p2 e - ap p 2	w' =-- - 2 A— - 2 e -ap + p p

Заключение. Направления динамического синтеза дополнительных цепей обратной связи могут быть, как показано выше, построены на комбинационных построениях механической цепи из типовых элементарных звеньев, однако такой методический прием не единственный. Приведенные результаты могут быть, в частности, получены путем редукции выражения (1). Последняя заключается в том, что, зануляя соответствующие коэффициенты выражения (1), можно получать не только передаточные функции традиционного и расширенного наборов типовых элементов, но и передаточные функции типовых структур второго уровня, а также более сложных структур, соответствующих задачам активной виброзащиты и виброизоляции.

Характерным обстоятельством, которое хотелось бы отметить, является то, что, выбрав передаточную функцию частного вида из выражения (1), одновременно можно получить возможность предварительной оценки динамических свойств с последующим выбором способов физической реализации такой цепи. В этом плане могут быть рассмотрены, как минимум, три направления:

• –    комбинация элементарных звеньев расширенного типового набора;

• –    комбинации через соединения типовых звеньев на основе правил структурного преобразования;

• –    поиск физических реализаций механических систем, имеющих передаточную функцию частного вида от выражения (1) на основе механизмов различного вида или сервоприводов.