Точечные дефекты в нематических жидкокристаллических материалах с коническим сцеплением на границе раздела
Автор: Крахалев М.Н., Шабанов В.Ф., Зырянов В.Я.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Технологические процессы и материалы
Статья в выпуске: 3 т.21, 2020 года.
Бесплатный доступ
Исследованы топологические точечные дефекты в нематических жидкокристаллических материалах. Предложен метод наклонного падения света, позволяющий определять азимутальный угол директора ахирального нематика, а также закрученного нематика (холестерика). Суть метода состоит в том, что при наклонном падении света на структуру с отличным от 0° и 90° полярным углом директора нематического жидкого кристалла (конические граничные условия) оптическая разность фаз, возникающая между обыкновенным и необыкновенным лучами, определяется величиной азимутального угла директора в центре слоя. Показано, что максимальное значение разности фаз достигается при нулевом азимутальном угле в центре слоя независимо от полного угла закрутки директора. Разработанный метод был использован для анализа топологических дефектов, формирующихся в слоях нематика и холестерика с коническими граничными условиями на межфазной границе. На основании полученных экспериментальных данных были построены распределения поля директора нематика и холестерика вблизи поверхностных точечных дефектов (буджумов) с топологическими зарядами m = +1 и m = -1. Полученные результаты интересны для исследований структурированных материалов, анализа оптическими методами дефектов структур, а предложенный метод наклонного падения света может использоваться для анализа широкого класса ахиральных и хиральных жидкокристаллических сред различного типа: смектиков, нематиков и холестериков с наклонными или гибридными граничными условиями.
Топологический дефект, ориентационная структура, нематический жидкий кристалл, оптическая разность фаз
Короткий адрес: https://sciup.org/148321993
IDR: 148321993 | УДК: 539.22 | DOI: 10.31772/2587-6066-2020-21-3-433-440
Текст научной статьи Точечные дефекты в нематических жидкокристаллических материалах с коническим сцеплением на границе раздела
Введение. Жидкие кристаллы (ЖК) – анизотропные жидкости, обладающие дальним ориентационным порядком молекул. Ориентация молекул ЖК характеризуется директором n – единичным вектором, ориентированным вдоль преимущественной ориентации длинных осей молекул [1]. В ЖК возможно богатое разнообразие формирующихся конфигураций поля директора, зависящих от граничных условий (преимущественной ориентации директора на межфазной границы), материальных параметров ЖК (констант упругости, шага спирали), внешних электрических или магнитных полей [2]. При этом в системе возможно формирование дефектов, вблизи которых наблюдается значительные искажения поля директора. И наоборот, при индуцировании сильных искажений в объеме, например магнитными (электрическими) полями или внедрением в ЖК микрочастичек, происходит формирование топологических дефектов. Возникающие искажения поля директора способствуют взаимодействию между собой дефектов и частичек, что проявляется в эффектах самоупорядочения дефектов [3–5], коллоидных [6; 7] и магнитных [8] частичек, позволяет управлять положением микрочастичек [9] и определяет групповое движение дефектов во внешнем электрическом поле [10]. Таким образом, наличие топологических дефектов является важной особенностью, существенно влияющей на основные характеристики жидкокристаллических материалов (оптические, электрооптические, динамические), которые определяют их перспективность для различных приложений в современных информационных технологиях.
В нематических ЖК могут сформироваться точечные объемные (ежи) [11; 12] и поверхностные (буджумы) [13] дефекты, линейные дефекты [14] и двумерные дефекты – стенки [2]. В случае закрученного нематика с соотношением толщины слоя d и шага спирали pd / p ≈ 1 в системе могут образоваться солитоноподобные структуры [15] или линейные дефекты[16]. Возможность формирования и стабильность различных типов дефектов определяется граничными условиями, задаваемыми на подложках. Так, при вырожденных тангенциальных (планарных) граничных условиях (угол между директором и нормалью к поверхности равен 90°) в ЖК ячейке формируется шлирен-текстура, состоящая из точечных и линейных дефектов, сила которых зависит от соотношения констант упругости ЖК [17]. В случае гомеотропного сцепления (угол между директором и нормалью к поверхности равен 0°) исходно дефекты в системе отсутствуют, однако приложение электрического поля или комбинации электрического и магнитного полей способствуют формированию упорядоченного набора точечных дефектов [3], двумерных дефектов [2] или солитоноподобных структур в закрученном нематике [15]. При гомео-планарных граничных условиях в системе возможно формирование точечных дефектов на подложке с планарным сцеплением или структура доменов с замкнутыми линейными дефектами.
Конические граничные условия (директор ориентирован к нормали к поверхности под углом, отличным от 0° и 90°) являются более подходящими для возникновения дефектов. Например, в ячейке с коническим сцеплением происходит формирование точечных, линейных и двумерных дефектов даже в отсутствие внешних полей [18]. В случае закрученного нематика с планарно-коническим сцеплением образуются линейные дефекты [19] или домены, ограниченные замкнутым линейным дефектом с парой точечных особенностей [20]. При этом на сегодняшний день точечные дефекты в ЖК системах с коническим сцеплением практически не исследованы.
В данной работе впервые представлены результаты исследования структур точечных дефектов, формирующихся в нематике и закрученном нематике при конических граничных условиях на обеих подложках.
Материалы и методы. Исследования проводились для нематической смеси ЛН-396 (Белорусский государственный технологический университет) и ЛН-396, допированной лево-закручивающей хиральной добавкой холестерилацетата (SigmaAldrich).Концентрация холестерилацетата составляла 0,2 %, что определяет шаг спирали холестерика величиной p = 72,5 мкм[19].Исследования проводились в ЖК ячейках, состоящих из двух стеклянных подложек, собранных таким образом, что между ними образуется зазор, который заполняется жидким кристаллом (рис. 1, a ). Стеклянные подложки методом центрифугирования покрывались пленкой полиизобутилметакрилат (SigmaAldrich), который задает для используемого нематика ЛН-396 конические граничные условия с полярным углом θ d /2 = 40◦[21]. Толщина d ЖК слоя задавалась стеклянными шариками и измерялась интерференционным методом до заполнения ячейки жидким кристаллом. ЖК ячейки заполнялись при комнатной температуре и выдерживались не менее 24 часов до проведения исследований. Исследования проводились с помощью поляризационного микроскопа (POM) AxioImager.M1m (CarlZeiss) с использованием длиннофокусного объектива 20x/0.22 в монохроматическом свете с длиной волны λ = 546 нм. Показатели преломления ЖК ЛН-396 равны n ꓕ = 1.528, n ‖ = 1.741 (λ = 546 нм).
Метод наклонного падения света. Распределение поля директора в ячейке удобно описывать с помощью полярногоθ( x , y , z ) и азимутального φ( x , y , z ) углов (рис. 1, b ). В этом случае директор n описывается уравнением:
пх = sin(0[x,y,z])cos(p[x,y,z]) ny = sin(9[x,y,z])sin(p[x,y,z]) nz = cos(9[x,y,z])
В общем случае углы θ и φ могут изменяться как по толщине ЖК слоя, так и в плоскости подложек. В большей степени это характерно для участков ЖК вблизи дефектов, при этом характер изменения углов определяется типом дефекта. И наоборот, по характеру изменения углов в окрестности дефекта можно определить его параметры. В случае точечных дефектов нематиков, для этого, например, используют метод флуоресцентной микроскопии [22]. В случае наклонной ориентации директора в объеме, которая реализуется при конических граничных условиях, для характеристики дефектов удобно использовать метод наклонного падения света, предложенного и описанного далее.
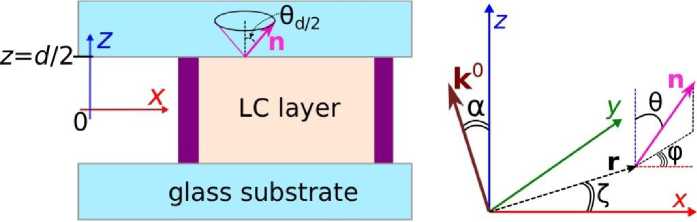
a b
Рис. 1. Схематическое представление ЖК ячейки ( a ) и система координат, используемая для расчетов оптической разности фаз в случае наклонного падения света и поля директора вокруг буджумов ( b )
Fig. 1. Scheme of LC cell ( a ) and the coordinate system used to calculate the optical phase difference at oblique light incidence and the director field around the boojums ( b )
Рассмотрим закрученный нематик вдали от дефектов. В этом случае можно полагать, что полярный угол директора постоянен и равен углу наклона директора на подложках θ( x , y , z ) = θ d /2 = θ -d /2 , а азимутальный угол φ( x , y ) зависит от координаты z по линейному закону:
P (x, y, z) = <0 (x, y) + ‘p™11 z, (2)
где φ 0 ( x , y ) – азимутальный угол директора в центре слоя (при z = 0), φ TOTAL - разность азимутальных углов директора на верхней ( z = + d /2) и нижней ( z = - d /2) подложках (полный азимутальный угол закрутки директора на толщине слоя d ). Рассмотрим наклонное в плоскости xOz падение луча света на слой ЖК (рис. 1b). Направление луча будем характеризовать единичным вектором k 0(±sinα, 0, cosα), где знак плюс соответствует нулевому азимутальному углу для вектора k 0, знак минус – значению азимутального угла вектора k 0 равному π. При выполнении условия Могена[23] можно положить, что в такой закрученной структуре распространяются две линейные волны, разность фаз между которыми в случае наклонного под углом α падения света определяется как:
6 = If1/. . "^”> dz' - nJ,
ZcOSaH- /2 Jn2+(n2-n2)CO52(0‘) / где z’ = z/d, а cos(θ’) равен:
cos(0') = nk0 = ±sina sin^dd^ cos(<0(x,y) + (Ptotal z') + cosa cos(dd^. (4)
На рис. 2 показаны зависимости от угла φ 0 ( x , y ) значения δ/ d , рассчитанные по уравнению (3) для нескольких значений полного угла закрутки φ TOTAL при наклонном падении под углом α = 5,33° (для случая, показанного на рис. 1, b ), и полярном угле θ d/2 = 40°. Видно, что в зависимостях наблюдается один максимум, соответствующий углу φ 0 ( x , y ) = 0°, а увеличение угла φ TOTAL приводит к незначительному уменьшению разности (δ max –δ min )/ d от значения примерно 0,43 рад/мкм до 0,27 рад/мкм для углов φ TOTAL 0° и 180°, соответственно. Такое различие разностей фаз, наблюдаемых для различных азимутальных углов φ 0 ( x , y ), может быть легко зафиксировано для обычно используемых толщин ЖК ячеек, составляющих порядка 10 мкм. При этом, используемый для расчета угол α позволяет легко проводить наблюдения с помощью поляризационного микроскопа, применяя длиннофокусный объектив. Данные, представленные на рис. 2, получены для положительного значения углов φ TOTAL (право-закрученный холестерик), при этом вследствие симметричности структуры относительно центра слоя идентичные результаты получаются и для отрицательных углов φ TOTAL (лево-закрученный холестерик).
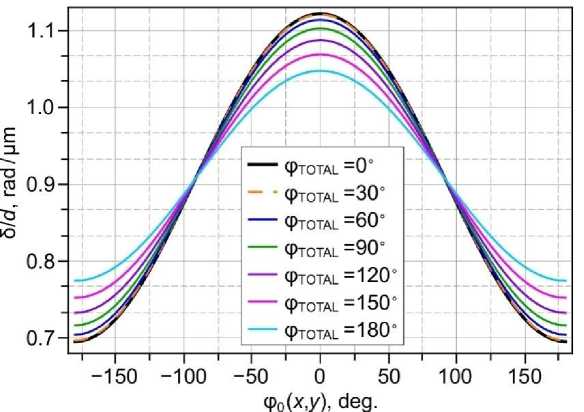
Рис. 2. Зависимости отношения δ/ d от угла φ 0 ( x , y ), рассчитанные для нескольких углов закрутки φ TOTAL . Расчет сделан для углов α = 5.33°, θ( x , y , z ) = θ d/2 = 40°, длины волны света λ = 546 нм и показателей преломления, соответствующих ЖК ЛН-396.
Fig. 2. Dependences of the ratio δ/ d on the angle φ 0 ( x , y ) calculated for some twist angles φ TOTAL . The data have been calculated for the angles α = 5.33°, θ( x , y , z ) = θ d/2 = 40°, the wavelength λ = 546 nm and the refractive indices corresponding to LC LN-396.
Приведенные выше результаты получены из предположения постоянства полярного угла директора θ и простой линейной зависимости азимутального угла φ от координаты z. В общем случае эти условия могут не выполняться. Так, например, в закрученной структуре нематика со значительными углами преднаклона директора на подложках полярный угол θ начинает зависеть от координаты z, одновременно с этим зависимость азимутального угла директора от координаты z отклоняется от линейного закона [24]. Тем не менее, результаты, полученные для простых случаев, показывают, что максимальное значение δ достигается при φ0(x, y) = 0° независимо от значений угла θd/2и φTOTAL. Соответственно, этот вывод можно распространить на случай неоднородного наклона и неравномерного угла закрутки в случае, если распределение директора в объеме симметрично относительно центра слоя. Именно такая ситуация реализуется в ЖК ячейках при одинаковых граничных условиях в отсутствии внешних воздействий (например, электрического поля). Далее данный метод будет применен для анализа буджумов, формирующихся в нематике и закрученном нематике при конических граничных условиях.
Буджумы в нематике. В отсутствие заданной ориентации директора на подложках (вырожденные тангенциальные или конические граничные условия) в системе формируются точечные дефекты на поверхности – буджумы. Вблизи буджумов ориентацию директора на поверхности (плоскость z = d /2) можно описать как [25]:
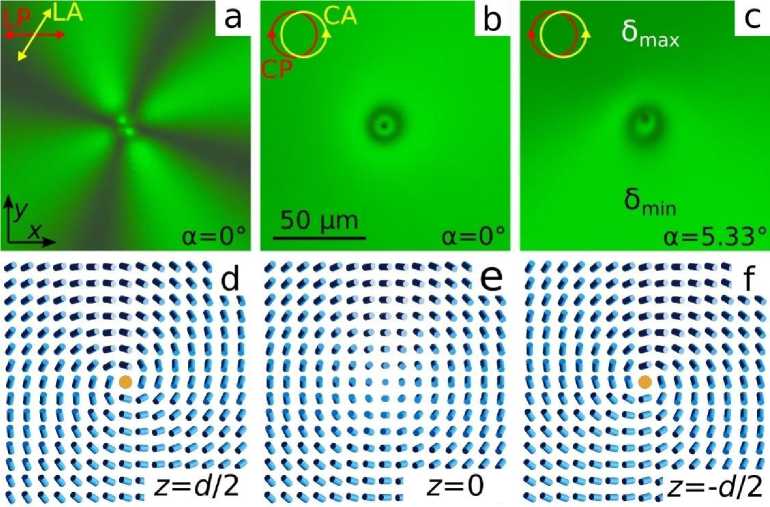
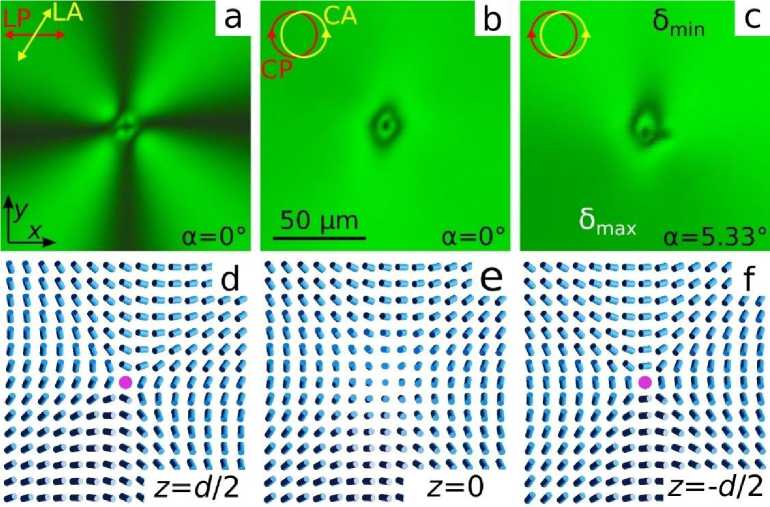
пх = sin (^d/ ) cosCm^ + () ny = sin (^d/2) sin(m< + где ζ –угол в полярной системе координат (см. рис. 1, b), m – поверхностный топологический заряд (сила) дефекта, -π ≤ ξ < π – угол закрутки буджума. Сила дефекта m и угол ξ используются для классификации буджумов (как и топологических дефектов других типов), и, соответственно, определение этих двух параметров достаточно для того, чтобы охарактеризовать свойства топологических дефектов. В ЖК ячейки имеется две подложки, и появление буджума на одной из подложек (например, верхней при z = d/2) должно сопровождаться формированием точечного дефекта на второй (нижней при z = –d/2) подложке. Минимуму упругой энергии будет соответствовать идентичное распределение директора вблизи буджумов на верхней и нижней подложках (вытекание в третье измерение). Для определения заряда m проводят наблюдения образца в геометрии скрещенных линейных поляризаторов (LP). В этом случае из дефекта выходят линии погасания, количество которых N связанно с зарядом дефекта простым соотношением: N = |m|⋅4 (рис. 3a). Определить знак m можно, поворачивая поляризаторы относительно образца или проведя наблюдения в циркулярных поляризаторах (CP). В случае буджумов с m = +1 интерференционная картина, наблюдаемая в геометрии циркулярных поляризаторов, вблизи дефектов будет иметь радиальную симметрию, в то время как для буджумов с m = -1, вследствие неравенства splay, band и twist констант упругости ЖК, интерференционная картина будет иметь более низкую симметрию (рис. 3b). В случае нематика полный угол закрутки директора φTOTAL = 0, соответственно азимутальный угол директора оказывается независящим от координаты zи равенφ0(x, y). Поскольку, в окрестности буджумов азимутальный угол директора изменяется в диапазоне -180° ≤ φ(x, y) = mζ+ξ ≤180°, то определить угол закрутки ξ можно используя метод наклонного падения света. В этом случае, при реализации схемы, показанной на рис. 2, δmax наблюдается при условии (mζ+ξ) = 0, а δmin соответствует условию (mζ+ξ) = π(–π). Для применения данного метода удобно использовать циркулярные поляризаторы. На рис. 3 показаны буджумы с |m| = 1, что видно из наблюдений в геометрии скрещенных линейных поляризаторов. При наблюдении в геометрии скрещенных циркулярных поляризаторов наблюдаемая интерференционная картина определяется только разностью фаз между обыкновенной и необыкновенной волной. Видно, что интерференционная картина в окрестности буджумов соответствует случаю, когда при движении от буджума к периферии происходит увеличение разности фаз от нуля до δ > 4π, что хорошо согласуется с параметрами ЖК ячейки, имеющей толщину ЖК слоя d = 14.6 мкм и угол наклона директора θd/2 = 40°, для которых из уравнения (3) при α = 0° и φTOTAL = 0 получается значение δ = 4.17π. Это соответствует вышеописанной ситуации, когда буджумы на верхней и нижней подложках располагаются один напротив другого (вытекание в третье измерение). В геометрии скрещенных линейных поляризаторов из буджума с m = +1 (Рис. 3, первый ряд) выходят четыре полосы погасания, параллельные поляризаторам. При наблюдении в циркулярных поляризаторах интерференционная картина симметрична в случае нормального падения света (α = 0°) (рис. 3b, первый ряд). В случае наклонного падения света под углом α = 5,33° симметрия интерференционной картины нарушается (рис. 3, c, первый ряд). По характеру изменения яркости наблюдаемой интерференционной картины можно сделать вывод, что максимальная разность фаз δmax соответствует линии погасания, ориентированной под углом ζ = –90°, а δmin соответствует значению угла ζ = –90°. Это означает, что угол закрутки буджума на верхней подложке ξ = 90° (рис. 3, d, первый ряд). Аналогичным образом можно определить угол закрутки буджума с зарядом m = –1 (рис. 3, второй ряд). В геометрии скрещенных линейных поляризаторов (при α = 0°) линии погасания образуют прямой крест, ориентированный под углом 15° к направлению линейного поляризатора LP. Из интерференционной картины, наблюдаемой при наклонном (α = 5.33°) падении света в геометрии циркулярных поляризаторов видно, что δmax соответствует линии погасания, ориентированной под углом ξ = -75°, что соответствует углу закрутки буджума на верхней подложке ξ = –75° (рис. 3, d, второй ряд). Рис. 3. POM фотографии участков образца нематика с буджумами, имеющими силу m = +1 и угол закрутки ξ = 90º (первый ряд), m = –1 и угол закрутки ξ = –75º (второй ряд). Фотографии сделаны в монохроматическом свете (λ = 546 нм) в геометрии скрещенных линейных поляризатора (LP) и анализатора (LA) для ориентации поляризатора LP 0º (a), скрещенных циркулярных поляризатора (CP) и анализатора (CA) для углов падения света α = 0° (b) и α = 5.33° (c). Рассчитанные по уравнению (5) соответствующие распределения поля директора на верхней подложке (d) Fig. 3. POM photos of the sample areas of nematic with boojums of m = +1 strength and the twisting angle ξ = 90º (the first row), m = –1 and ξ = –75º (the second row). The photos were taken in the monochromatic light (λ = 546 nm) for the crossed linear polarizer (LP) and analyzer (LA) at the polarizer orientation LP 0º (a), for the crossed circular polarizer (CP) and analyzer (CA) at the light incidence angle α = 0° (b) and α = 5.33° (c). The corresponding director field distributions on the top substrate calculated by eq. (5) (d) Следует отметить, что в образце наблюдаются буджумы с зарядом m = +1, имеющие угол закрутки ξ, близкий к значению ±90°. Таким образом, буджум с m = +1 и |ξ| = 90° наиболее энергетически выгоден для ЖК ЛН-396 в случае угла наклона директора θd/2 = 40°. Для буджумов с зарядом m = –1 наблюдаются различные углы закрутки ξ. Это является следствием того, что распределение поля директора вблизи буджума с m = –1 при различных углах ξ отличается только ориентацией осей симметрии, т. е. буджум с углом ξ можно получить, повернув всю структуру (систему координат) поля директора с ξ0 = 0 вокруг оси Oz на угол ξ/2 [25]. Таким образом, полная свободная энергия поля директора нематика вблизи буджумов с m = –1, в отличие от буджума с m = +1, не зависит от угла закрутки ξ. Буджумы в закрученном нематике (холестерике).Структуры холестерика исследовались для ячейки толщиной d = 12,7 мкм, что соответствует соотношению d/p = 0,18. В этом случае линии погасания наблюдаются для угла 58° между анализатором и поляризатором, что соответствует углу закрутки директора φTOTAL = –32° (рис. 4, a, 5, a). На рис. 4 показан буджум с m = +1, для которого полосы погасания образуют прямой крест, повернутый на угол –16° по отношению к направлению поляризатора. Наблюдение при наклонном падении света на ячейку (рис. 4, c) показывают, что δmax, а следовательно, и значение φ0(x, y) = 0 наблюдается при угле ζ ≈ 90°. В этом случае, в приближении линейной зависимости азимутального угла директора от координаты z (уравнение (2)), угол закрутки буджума на верхней подложке найдется из соотношения(+1·90° + ξ = φTOTAL/2), откуда ξd/2 = –106°(рис. 4, d), в то время как на нижней подложке ξ-d/2 = –74° (рис. 4, f). Ориентация четырех линий погасания соответствует условию, когда φ-d/2 равен 0°, ±90° и –180°, что соответствует углам 74°, 164°, –16°, –106° и согласуется с ориентацией полос погасания, наблюдаемых в геометрии скрещенных поляризаторов (рис. 4, a). Рис. 4. POM фотографии участка образца холестерика с буджумом, имеющим силу m = +1 и угол закрутки на верхней подложке ξ = –106º, сделанные в монохроматическом свете (λ = 546 нм)в геометрии скрещенных под углом 58° линейных поляризаторов для ориентации поляризатора LP 0º (a), скрещенных циркулярных поляризаторов для углов падения света α = 0° (b) и α = 5,33° (c). Рассчитанные по уравнению (5) с учетом условия (2) соответствующие распределения поля директора на верхней подложке (d), в центре слоя (e) и на нижней подложке (f) Fig. 4. POM photos of the sample area of cholesteric with boojum of m = +1 strength and the twisting angle on the top substrate ξ = –106º taken in the monochromatic light (λ = 546 nm) for the crossed at 58° angle linear polarizers at the polarizer orientation LP 0º (a), for the crossed circular polarizers at the light incidence angle α = 0° (b) and α = 5.33° (c). The corresponding director field distributions on the top substrate (d), at the layer center (e) and on the bottom substrate (f) calculated by equation (5) considering the conditions (2) Аналогичным образом можно определить угол закрутки буджумов с m = –1 (рис. 5). Крест, который образуют линии погасания ориентирован под углом примерно 5° к поляризатору (рис. 5, a), в то время как δmax достигается при угле ζ ≈ –100° (рис. 5, c). Это соответствует углу закрутки буджума на верхней подложке, который находится из соотношения (–1·(–100°) + ξ = φTOTAL/2), откуда ξ = –116° (рис. 5, d). На нижней подложке ему соответствует буджум с ξ = -84° (рис. 5, f). Рис. 5. POM фотографии участка образца холестерика с буджумом, имеющими силу m = –1 и угол закрутки на верхней подложке ξ = –116º, сделанные в монохроматическом свете (λ = 546 нм) в геометрии скрещенных под углом 58° линейных поляризаторов для ориентации поляризатора LP 0º (a), скрещенных циркулярных поляризаторов для углов падения света α = 0° (b) и α = 5,33° (c). Рассчитанные по уравнению (5) с учетом условия (2) соответствующие распределения поля директора на верхней подложке (d), в центре слоя (e) и нижней подложке (f) Fig. 5. POM photos of the sample area of cholesteric with boojum of m = –1 strength and the twisting angle on the top substrate ξ = –116º taken in the monochromatic light (λ = 546 nm) for the crossed at 58° angle linear polarizers at the polarizer orientation LP 0º (a), for the crossed circular polarizers at the light incidence angle α = 0° (b) and α = 5.33° (c). The corresponding director field distributions on the top substrate (d), at the layer center (e) and on the bottom substrate (f) calculated by equation (5) considering the conditions (2) Заключение. В данной работе нами предложен метод наклонного падения света на ЖК ячейку, позволяющий определять полярный и азимутальный углы ориентации директора в случае конических граничных условий. Возможности данного метода были продемонстрированы на примере точечных топологических дефектов-буджумов, формирующихся в нематике с углом наклона директора на границе θd/2 = 40°, для которых впервые были определены сила дефекта m и углы закрутки ξ. Показано, что в используемом нематическом ЖК ЛН-396 имеется тенденция формирования буджумов с m = +1, имеющих угол закрутки ξ = ±90°.Данный метод применим и для закрученной структуры холестерика. При этом, в случае выполнения режима Могена, максимальная разность фаз δmax между обыкновенным и необыкновенным лучами достигается при азимутальной ориентации директора в центре слоя φ0(x, y) = 0 независимо от полного угла закрутки директора φTOTAL.С использованиемпредложенного метода нами была определена ориентационная структура буджумов, формирующихся на верхней и нижней подложках, задающих коническое сцепление для ЖК. Полученные результаты представляют интерес для исследований структурированных материалов, анализа оптическими методами дефектов структур, а разработанный метод наклонного падения света может потенциально использоваться для анализа широкого класса оптически анизотропных и хиральных сред, таких как смектики, нематики и холестерики с наклонными или гибридными граничными условиями. Необходимо отметить прикладную значимость результатов исследования, поскольку жидкокристаллические среды на сегодняшний день остаются наиболее конкурентными функциональными материалами для применения в оптоэлектронных устройствах, требующих малую массу и габариты, низковольтное управление и малое энергопотребление, что, например, весьма актуально для применения в космических технологиях.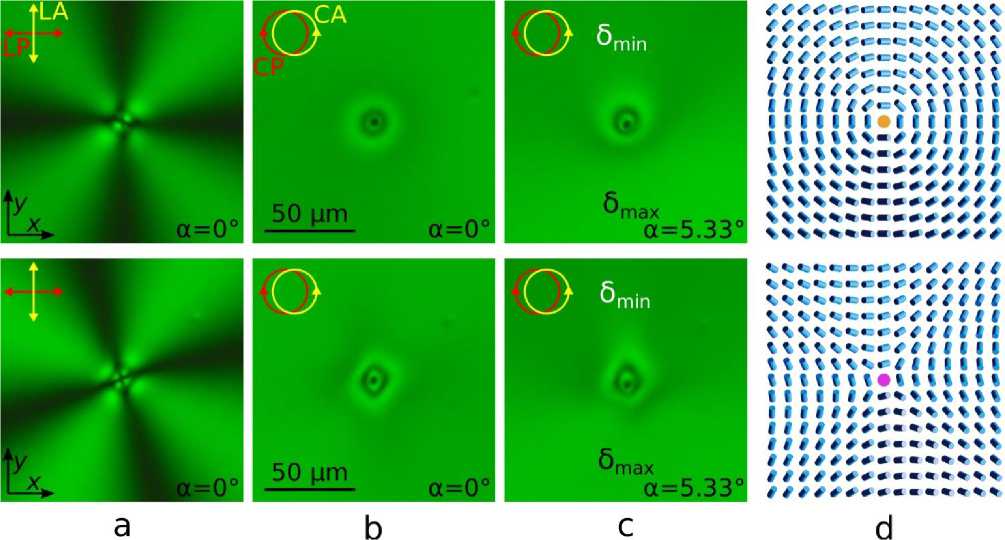
Список литературы Точечные дефекты в нематических жидкокристаллических материалах с коническим сцеплением на границе раздела
- Gennes P. G. de, Prost J. The physics of liquid crystals. 2. ed., Reprint. Oxford: Clarendon Press, 1998. 597 p.
- Oswald P., Pieranski P. Nematic and cholesteric liquid crystals: concepts and physical properties illustrated by experiments. Boca Raton: Taylor & Francis, 2005. 618 p.
- Sasaki Y. et al. Large-scale self-organization of reconfigurable topological defect networks in nematic liquid crystals. Nature Communications. 2016, Vol. 7, No. 1, P. 13238.
- Kim M., Serra F. Tunable dynamic topological defect pattern formation in nematic liquid crystals. Advanced Optical Materials. 2020, Vol. 8, No. 1, P. 1900991.
- Kim M., Serra F. Topological defect arrays in nematic liquid crystals assisted by polymeric pillar arrays: effect of the geometry of pillars. Crystals. 2020, Vol. 10, No. 4, P. 314.
- Senyuk B. et al. Topological colloids. Nature. 2013, Vol. 493, No. 7431, P. 200-205.
- Nych A. et al. Assembly and control of 3D nematic dipolar colloidal crystals. Nature Communications, 2013, Vol. 4, No. 1, P. 1489.
- Medle Rupnik P. et al. Field-controlled structures in ferromagnetic cholesteric liquid crystals. Science Advances. 2017, Vol. 3, No. 10, P. 1701336.
- Lavrentovich O. D. Transport of particles in liquid crystals. Soft Matter. 2014, Vol. 10, No. 9, P. 1264-1283.
- Sohn H. R. O., Liu C. D., Smalyukh I. I. Schools of skyrmions with electrically tunable elastic interactions. Nature Communications. 2019, Vol. 10, No. 1, P. 4744.
- Sengupta A. Microbial active matter: A topologi-cal framework. Front. Phys. Frontiers. 2020, Vol. 8, P. 184.
- Nabarro F. R. N. Singular lines and singular points of ferromagnetic spin systems and of nematic liquid crystals. Journal de Physique. 1972, Vol. 33, No. 11-12, P. 1089-1098.
- Meyer R. B. Point disclinations at a nematic-isotropic liquid interface. Molecular Crystals and Liquid Crystals. 1972, Vol. 16, No. 4, P. 355-369.
- Kleman M., Friedel J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev. Mod. Phys. 2008, Vol. 80, No. 1, P. 61-115.
- Oswald P., Baudry J., Pirkl S. Static and dynamic properties of cholesteric fingers in electric field. Physics Reports. 2000, Vol. 337, No. 1, P. 67-96.
- Smalyukh I. I., Lavrentovich O. D. Three-dimensional director structures of defects in Grandjean-Cano wedges of cholesteric liquid crystals studied by fluorescence confocal polarizing microscopy. Phys. Rev. E. 2002, Vol. 66, No. 5, P. 051703.
- Madhusudana N. V., Pratibha R. Studies on high strength defects in nematic liquid crystals. Molecular Crystals and Liquid Crystals. 1983, Vol. 103, No. 1-4, P. 31-47.
- Ryschenkow G., Kleman M. Surface defects and structural transitions in very low anchoring energy nematic thin films. Journal of Chemical Physics. 1976, Vol. 64, No. 1, P. 404-412.
- Krakhalev M. N. et al. Nematic and cholesteric liquid crystal structures in cells with tangential-conical boundary conditions. Crystals. 2019, Vol. 9, No. 5, P. 249.
- Krakhalev M. N. Electrically induced transformations of defects in cholesteric layer with tangential-conical boundary conditions. Scientific reports. 2020. Vol. 10. P. 4907.
- Krakhalev M.N. et al. Director configurations in nematic droplets with tilted surface anchoring. Liquid Crystals. 2017, Vol. 44, No. 2, P. 355-363.
- Ohzono T. Uncovering different states of topological defects in schlieren textures of a nematic liquid crystal. Scientific reports. 2017, Vol. 7, P. 16814.
- Yeh P., Gu C. Optics of liquid crystal displays. New York, Wiley, 1999, 438 p.
- Lien A. The general and simplified Jones matrix representations for the high pretilt twisted nematic cell. Journal of Applied Physics. 1990, Vol. 67, No. 6, P. 2853-2856.
- Harth K., Stannarius R. Topological point defects of liquid crystals in quasi-two-dimensional geometries. Front. Phys. Frontiers. 2020, Vol. 8, P. 112.


