Точки минимума давления в осесимметричных течениях жидкости
Автор: Голубкин В.Н., Сизых Г.Б.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Механика
Статья в выпуске: 2 (34) т.9, 2017 года.
Бесплатный доступ
Показано, что при отсутствии точек торможения в ограниченной области осесим- метричного вихревого течения идеальной несжимаемой жидкости давление достигает минимального значения на границе области. Нарушение этого свойства давления сви- детельствует о наличии внутренней точки торможения. Полученный вывод может быть использован для верификации численных расчетов течения при обтекании тел враще- ния.
Уравнения эйлера, вихревые течения, принцип минимума дав- ления, осесимметричные течения, несжимаемая жидкость
Короткий адрес: https://sciup.org/142186187
IDR: 142186187 | УДК: 533.6.011
Текст научной статьи Точки минимума давления в осесимметричных течениях жидкости
Давление в стационарных безвихревых течениях идеальной несжимаемой жидкости не может достигать минимума во внутренней точке течения. Этот факт следует из теории гармонических функций. Для вихревых течений идеальной жидкости известен принцип Роуланда [1], предлагающий различные утверждения о минимуме или о максимуме давления, в зависимости от знака некоторой функции Q , для определения которой нужно знать первые производные компонент скорости (см. ниже). Позже этот принцип был обобщен Гамелем [2] на случай вязкой несжимаемой жидкости. В свою очередь, принцип Гамеля был обобщен Трусделлом [3] (см. также [4, §28]) на случай сжимаемой жидкости. Однако оба эти обобщения не дают новых утверждений для идеальной несжимаемой жидкости, поскольку в этом случае они сводятся к изначальному принципу Роуланда, который практически непригоден для априорных выводов, поскольку знак функции Q трудно указать заранее.
В работе [5] обнаружено свойство экстремальных значений давления в плоском вихревом течении идеальной жидкости: если в ограниченной области течения жидкости отсутствуют точки торможения и давление p не постоянно всюду, то и максимум и минимум p достигаются только на границе области.
В данной статье обоснован принцип минимума давления в осесимметричных вихревых течениях идеальной жидкости, условия которого совпадают с условиями принципа [5] и поэтому имеют более обозримый и идентифицируемый вид, чем условия Роуланда.
Полученный принцип минимума можно применить к практически важным осесимметричным течениям.
2. Принцип минимума давления в осесимметричном течении идеальной жидкости
Рассмотрим пространственное стационарное течение идеальной несжимаемой жидкости в замыкании G некоторой ограниченной области G . Такое течение описывается уравнениями Эйлера:
Q x V = - 1 Vp — 1VV 2 , (1)
P 2
div V = 0 , (2)
где p - давление, V - вектор скорости, p = const — плотность жидкости, Q = rot V -завихренность, V = | V | , V - оператор Гамильтона.
Будем считать, что в рассматриваемой области отсутствуют точки торможения, то есть
V > 0 .
При этом допускается наличие точек торможения ( V = 0) на границе области.
Также будем считать, что все гидродинамические функции являются дважды непрерывно дифференцируемыми функциями координат в области G и непрерывными на ее замыкании G .
Покажем, что для осесимметричных течений при выполнении указанных условий справедлив принцип минимума давления: если давление не постоянно в области G , то оно достигает минимального значения только на границе этой области.
Для доказательства введем трехмерную прямоугольную декартову систему координат Oxyz и обозначим через u, v , w соответствующие компоненты вектора скорости. Вычисляя дивергенцию обеих частей векторного уравнения (1), получим
- A p = Q 2 — V • rot Q-- А V 2 ,
P 2
где А - оператор Лапласа.
Учитывая, что 2 А V 2 = V • AV + ( Vu ) 2 + ( Vv ) 2 + ( Vw ) 2 и что для несжимаемой жидкости V • rot Q = — V • AV , из (4) после перестановки слагаемых получим
1А p = Q 2 — ( Vu ) 2 — ( Vv ) 2 — ( Vw ) 2 . ρ
Замечание. Уравнение (5) известно давно [1]. Функция Q , о которой говорилось во введении, есть половина правой части (5). Если во всей области Q ^ 0 или Q ^ 0, то уравнение (5) становится супер- или субгармоническим, и давление (если не постоянно всюду) не может достигать во внутренней точке течения соответственно минимума или максимума. В этом состоит принцип Роуланда. Однако до сих пор знак параметра Q можно было априорно указать только для безвихревых течений, в которых Q ^ 0. В данной статье предложен способ исследования экстремальных свойств давления для незакручен-ных осесимметричных течений без выяснения знака параметра Q . Для этого уравнение (5) преобразовано к другому виду, допускающему применение теоремы Хопфа [6, 7].
Уравнение (5) верно для общего 3D-случая. Далее рассмотрим незакрученные осе- симметричные течения и воспользуемся присущим им свойством перпендикулярности
(Q V ) 2 = ( Р Vp + 2 VV 2 ) 2 ,
векторов скорости и завихренности. Тогда из (1) следует, что или, учитывая принятое выше предположение (3) об отсутствии точек торможения (V = 0),
П 2 = 5 2 , 2 ( Vp ) 2 + ^Vp • VV 2 + V , ( 2 VV 2 ) 2 =
= ( 5 2 V 2 Vp + , VV 2 ) -Vp + V , ( 2 VV 2 ) 2 .
Подставляя это выражение для квадрата завихренности в (5), получим
5 А p - {^ v p + 5V 2 V V 2) V =
= V 2 ( 2 VV 2 ) - ( Vu ) 2 - ( Vv ) 2 - ( Vw ) 2 .
Левая часть этого уравнения инвариантна относительно выбора системы координат Oxyz . Следовательно, правая часть
I =
V 2 ( 2 VV 2 ) — ( Vu ) 2 — ( Vv ) 2 — ( Vw ) 2
также инвариантна, то есть ее значение не зависит от выбора системы координат Oxyjz. Возьмем произвольную точку области G и расположим систему координат Oxyjz так, чтобы положительное направление оси Ox совпало с направлением скорости V . Тогда в выбранной точке соответствующие компоненты скорости будут U = V > 0 , V = 0 , w z = 0. Следовательно, в этой точке
I = ' 2 ( uVu + VVv + wVw j) 2 - ( Vz) 2 - ( VV ) 2 - ( Vw j) 2 = - ( VV ) 2 - ( Vw j) 2 ^ 0 .
Поскольку точка была выбрана произвольно, неравенство I ^ 0 выполнено во всей области
G. Поэтому во всех точках области G уравнение (6) можно записать в виде аp- (-12Vp + VV21 -Vp = f,
ρV 2 V 2
где правая часть неположительна: f = pI ^ 0.
Вернемся к выбранной с самого начала системе координат Oxyz. Если записать левую часть последнего уравнения в координатной форме, то второе слагаемое примет вид: b 1 dx + b2 dp + b3 dp, где коэффициенты b 1, b2 и b3 суть компоненты вектора, записанного в фигурных скобках, и зависят не только от гидродинамических функций u, v , w, p,но и от их первых производных. Таким образом, уравнение (6), которое является следствием уравнений Эйлера, может быть представлено в виде a 11 дл + 2 a 12 д^Л + a 22 ІЛ + 2 a 13ТЛГ + 2 a 23 d.p + a-3 Й + ∂x2 ∂x∂y ∂y2 ∂x∂z ∂y∂z ∂z2
+b 1 dp + b 2 dp + b 3 dp = f, (7) ∂x ∂y ∂z где коэффициенты a 11 = a22 = a33 = 1, a 12 = a 13 = a23 = 0 и функция f ^ 0.
Для анализа свойств решения уравнения (7) (в предположении, что оно существует) воспользуемся одним из следствий теоремы Хопфа [6, 7], приведенным в работе [8]. Это следствие специально сформулировано для использования в аэрогидродинамике. Сформулируем его с использованием обозначений данной статьи.
Пусть во всех точках ограниченной области G коэффициенты a11, a12, a22, a13, a23 и a33 уравнения (7) являются коэффициентами положительно определенной квадратичной формы A. Пусть, далее, для любой точки M(x, y, z) G G существуют числа ш = ш(x,y,z) > 0 и А = А(x,y,z) > 0 такие, что замкнутый круг U(M; ш) целиком лежит в области G и в нем все коэффициенты уравнения (7) ограничены и выполняется неравенство det A > A. И пусть во всех точках области G выполняется неравенство f С 0.
Тогда если решение p Е C 2 ( G ) уравнения (7) непрерывно в замкнутой области G, то p ^ min p во всей области G. При этом, если p = const в G, равенство p = min p возможно только на ∂G.
Если учесть, что согласно (3) скорость не обращается в нуль во внутренних точках области G , несложно проверить, что уравнение (7) удовлетворяет всем условиям приведенного следствия теоремы Хопфа. Отсюда следует, что при отсутствии точек торможения в ограниченной области осесимметричного вихревого течения идеальной несжимаемой жидкости давление достигает минимального значения только на границе области.
3. Случай наличия точек торможения
Проиллюстрируем существенность требования отсутствия точек торможения для полученного принципа минимума. Приведем пример, в котором нарушение этого требования приводит к «появлению» внутренней точки минимума давления.
Введем цилиндрическую систему координат r, ϕ, z с началом в точке O и будем рассматривать симметричные относительно оси Oz течения. Пусть e r , e ϕ , e z – правая тройка единичных векторов в радиальном, окружном и осевом направлениях соответственно. Вектор скорости незакрученного течения имеет вид V = V r e r + V z e z , где компоненты скорости V r и V z зависят только от переменных r , z .
В данном разделе все величины r , z , V r , V z и давление p, отнесенное к плотности, будем считать безразмерными. (Размерные величины координат г, ), компонент скорости V r , V z и давления p можно выразить через безразмерные переменные по формулам: r = rL , г = zL , V r = V r U , V z = V z U и p = p pU 2 , где L и U - характерные значения длины и скорости в рассматриваемом течении.)
Будем искать точное решение уравнений (1) и (2) в виде
V r = - ( g ( r )sin z )/ r, V z = -(g ' ( r )cos z)/r, (8)
p = 2 - ( g ( r ) cos z ) 2 - 0 . 5 ( V r 2 + V z 2) , (9)
где g = g ( r ) - некоторая функция одной координаты r . Если записать уравнения (1) и (2) в цилиндрической системе координат r, ϕ, z и подставить в них выражения (8) и (9), то эти уравнения окажутся выполненными, если функция g удовлетворяет обыкновенному дифференциальному уравнению (здесь и далее штрих означает дифференцирование по аргументу r ):
g " - r - g + 2 r 2 g = 0 . (10)
Рассмотрим задачу Коши для уравнения (10) на отрезке 0 . 75 С r С 1 • 25 с условиями, заданными в середине отрезка:
g (1) = 1 ,g (1) = 0 . (11)
Эта задача состоит из двух «стандартных» задач Коши. Одна из них – для уравнения (10) на отрезке 0 . 75 С r С 1 с условиями (11) на правом конце отрезка. Другая - для уравнения (10) на отрезке 1 С r С 1 • 25 с условиями (11) на левом конце отрезка.
Коэффициенты уравнения (10) ограничены на отрезке 0 . 75 С r С 1 • 25. Поэтому решение задачи Коши (10), (11) на отрезке 0 . 75 С r С 1 • 25 существует и единственно. Формулы (8) и (9), в которых g ( r ) является решением этой задачи, дают точное решение уравнений (1) и (2) в полосе 0 . 75 < r < 1 . 25 , -ж < z < + то . Рассмотрим прямоугольную область 0 . 75 < r < 1 . 25 , - 0 . 25 < z < 0 . 25. В выражения (8) и (9) входят функция g ( r ) и ее производная g' ( r ). Их графики, полученные в результате численного решения задачи (10), (11), представлены на рис. 1.
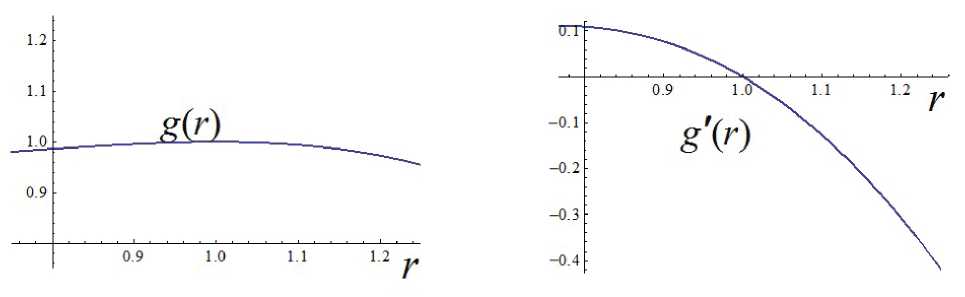
Рис. 1
Из (8) и (11) следует, что точка S с координатами r = 1 , z = 0 является точкой торможения ( V r = V z = 0). Линии тока этого течения показаны на рис. 2.
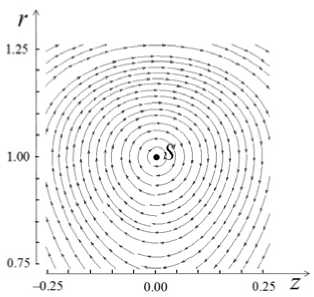
Рис. 2. Линии тока
Жидкость вращается вокруг точки S , и кривизна линий тока показывает, что давление должно уменьшаться по мере приближения к точке S . Поэтому в точке S будет минимум давления. Результаты расчетов в виде картины изобар с оттенками серого цвета приведены на рис. 3.
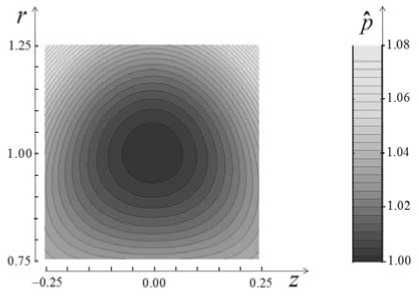
Рис. 3. Картина изобар
Расчеты показывают, что в рассматриваемой области точкой минимума давления является внутренняя точка S . Таким образом, при наличии внутренней точки торможения, когда условия установленного принципа минимума нарушаются, минимум давления может располагаться внутри области, а не на границе.
Численные расчеты проведены с высокой точностью. Тем не менее предложим строгое доказательство того, что точка S является точкой локального минимума давления. Из (8) и (9) следует, что д'' (1) = — 1. Это позволяет найти значения первых и вторых производных р(r,z ) в точке z = 0, r = 1. В итоге в окрестности точки S имеем разложение
р(1 + A r, A z ) = р (1 , 0) + (A r ) 2 + (A z ) 2 + o ^(A r ) 2 + (A z )2) , A r ^ 0 , A z ^ 0 , показывающее, что точка S действительно является точкой локального минимума давления.
4. Точки зарождения кавитации
В монографиях [9, 10] объясняется, почему кавитация при медленном увеличении скорости набегающего потока зарождается именно на поверхности обтекаемых тел. Объяснение основано на том, что точки минимума давления в безвихревых течениях находятся на границе. Подчеркнем, что эти выводы обоснованы в [9, 10] только для безвихревых (потенциальных) течений. Принцип работы [5] и принцип минимума давления, полученный в данной статье, позволяют сделать аналогичные выводы для плоских и осесимметричных вихревых течений. Кавитация в таких вихревых течениях должна зарождаться в точках минимума давления, которые расположены именно на поверхности обтекаемых тел.
5. Заключение
Обоснован принцип минимума давления для осесимметричных вихревых течений несжимаемой жидкости. Его условия имеют более обозримый вид, чем это было приведено в [1], и поэтому данный принцип можно использовать для априорных оценок, для качественного анализа течений и для верификации численных методов расчета наряду с полученными ранее принципами экстремальных значений [5, 11].
Список литературы Точки минимума давления в осесимметричных течениях жидкости
- Rowland H. On the motion of a perfect incompressible fluid when no bodies are present//American Journal of Mathematics. 1880. V. 3. P. 226-268.
- Hamel G. Ein allgemeiner Satz uber den Druck bei der Bewegung volumbestandiger Flussigkeiten//Monatshefte Math. Phys. 1936. V. 43. P. 345-363.
- Truesdell C. Two Measures of Vorticity//J Rational Mech. Anal. 1953. V. 2. P. 173-217.
- Серрин Дж. Математические основы классической механики жидкости. М.: Изд-во ИЛ, 1963.
- Голубкин В.Н., Ковалёв В.П., Сизых Г.Б. Принцип максимума давления в плоских течениях идеальной несжимаемой жидкости//Ученые записки ЦАГИ. 2016. Т. 47, № 6. С. 28-36.
- Hopf E. Elementare Bemerkungen uber die Losungen partieller Differentialgleichungen zweiter Ordnung vom Elliptischen Typus//Sitzungsberichte der Preussischen Akademie der Wissenschaften. 1927. V. 19. P. 147-152.
- Миранда К. Уравнения с частными производными эллиптического типа. М.: Издательство иностранной литературы, 1957.
- Беспорточный А.И., Бурмистров А.Н., Сизых Г.Б. Вариант теоремы Хопфа//Труды МФТИ. 2016. Т. 8, № 1. С. 115-122.
- Седов Л.И. Механика сплошной среды. Т. 2. М.: Наука, 1973.
- Бэтчелор Дж. Введение в динамику жидкости. М.: Мир, 1973.
- Голубкин В.Н., Сизых Г.Б. Принцип максимума функции Бернулли//Ученые записки ЦАГИ. 2015. Т. 46, № 5. С. 53-56.


