Точная и приближенная матрица жесткости и вектор узловых нагрузок балочного конечного элемента с линейным законом изменения жесткости по длине

Введение. В современной инженерной практике, особенно в контексте устойчивого развития и оптимизации ресурсов, активно применяются конструкции с переменной жёсткостью — например, балки переменного сечения [1] . Такие решения позволяют существенно снизить материалоёмкость и собственный вес конструкций, что прямо повышает их экономическую эффективность и экологичность за счёт сокращения расхода материалов [2] . Кроме того, математическая модель балки переменной жёсткости служит инструментом для качественного описания напряжённо-деформированного состояния железобетонных элементов, в которых изменение жёсткости происходит вследствие нелинейной работы материала [3, 4] и образования трещин [5, 6] .

В статически неопределимых балках, широко распространённых в строительной механике, распределение внутренних усилий зависит от соотношения жёсткостей элементов. Пренебрежение переменным характером жёсткости может привести к значительным ошибкам при определении внутренних усилий и, как следствие, к неверному подбору сечений, что ставит под угрозу как надёжность, так и экономическую целесообразность проекта. На рис 1 приведён наглядный пример — учёт переменной жёсткости в балке (рис. 1 б ) привёл к кардинальному изменению эпюры изгибающих моментов по сравнению с расчётной моделью постоянной жёсткости (рис. 1 а ).

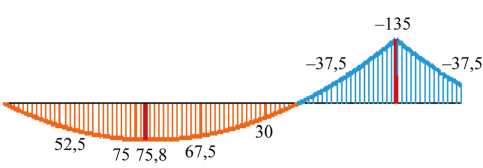
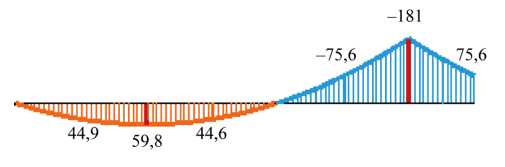
а)                                                            б)

Рис. 1. Результаты расчета статически неопределимой балки:

а — фрагмент статически неопределимой балки постоянной жесткости и эпюра изгибающих моментов в ней;

б — то же для балки переменной жесткости

Расчет балок переменного сечения традиционно осуществляется численными методами, в частности методом конечных элементов (МКЭ). Несмотря на существование аналитических решений [7] , они часто представлены в виде сложных рядов [8] или специальных функций [9] , что затрудняет их практическую реализацию в инженерном программном обеспечении. Кроме того, такие решения зачастую не обладают универсальностью для произвольных законов изменения жесткости и граничных условий [10, 11] .

Напряженно-деформированное состояние балок переменного сечения изучается различными авторами уже давно. В рамках численного расчета с применением МКЭ можно отметить одни из первых работ [12, 13] . Наиболее распространённым подходом к учёту переменной жесткости является дискретная аппроксимация с использованием конечных элементов постоянной жесткости (рис. 1 б ), значение которой принимается равным среднему на участке [14, 15] . Несмотря на простоту, такой подход не всегда обеспечивает требуемую точность расчетов.

Более точные результаты получаются при использовании линейной аппроксимации жесткости внутри конечного элемента. Такой подход применяется в рамках настоящей статьи. В то же время классические методы построения матриц жесткости для элементов с переменными параметрами [16] , основанные на вариационных подходах [17] или аппроксимациях [18] , могут не обеспечивать точного выполнения дифференциальных уравнений равновесия и граничных условий. Это приводит к погрешностям при существенном изменении жесткости по длине элемента или в предельных случаях — например, при моделировании зон с резким падением жесткости (образование трещин, пластического шарнира).

Таким образом, актуальность данного исследования обусловлена необходимостью разработки эффективного и более точного метода расчета балок переменной жесткости.

Цель настоящего исследования — получение и верификация матриц жесткости для конечного элемента балки с кусочно-линейным законом изменения жесткости.

Для достижения поставленной цели были сформулированы следующие задачи:

Механика

• 1.    На основе вариационной постановки задачи и линейной аппроксимации жесткости внутри конечного элемента получить приближённую матрица жесткости.

• 2.    Путём аналитического решения дифференциального уравнения изгиба получить точную матрицу жесткости для конечного элемента балки с линейно изменяющейся жесткостью.

• 3.    На серии тестовых примеров провести сравнительный анализ точности результатов расчёта с использованием предложенных матриц жесткости и классического подхода с дискретной аппроксимацией жесткости; точность определять путем сравнения с результатами аналитического решения.

Вариационный метод получения матрицы жесткости. Вариационные методы [19] являются общепринятыми и наиболее универсальными способами получения матрицы жесткости конечного элемента. Точность полученной матрицы зависит от того, насколько корректно вводимая аппроксимация искомой функции отражает решение дифференциального уравнения.

Для рассматриваемой балки применяются классические гипотезы Эйлера-Бернулли. Изменение изгибной жесткости поперечного сечения D z по длине конечного элемента принято в виде линейной функции:

D z ( x ) = D о

x

V о + l ( V i -V о )

, D z ( 0 ) = v о D о , D z ( L ) —V 1 D о ,

где D 0 — начальная жесткость; L — длина конечного элемента; ψ 0 и ψ 1 — коэффициенты, учитывающие изменение начальной жесткости D 0 в начале и конце элемента соответственно. При этом ψ 0 ≥ 0 и ψ 1 ≥ 0.

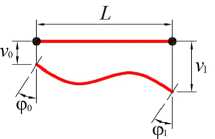
Метод конечных элементов рассматривается в форме перемещений. В качестве неизвестных выступают прогиб и угол поворота сечения v i и φ i (рис. 2 а ) в начале x = 0 и конце x = L элемента.

а)

б)

Рис. 2. Балочный конечный элемент:

а — неизвестные метода конечных элементов; б — узловые нагрузки и внутренние усилия

Для аппроксимации функции перемещений v ( x ) приняты полиномы Эрмита [1, 4] :

v = v о N 1 + фо N 2 + v 1 N3 + ф1 N 4, где Ni — функции формы (полиномы Эрмита), записанные ниже:

2 x ³    3 x ²             x ³

N = —5---r+1 ; N 2 =-5-

¹ L ³ L ^{2         2} L ²

—

2 x ²               2 x ³    3 x ²          x ³

+ x; N^ =--5—1—5~ ; N 4 = —7

L ³ L ³ L ^{2     4} L ²

—

x ² L

.

Аппроксимация (2) соответствует следующим граничным условиям:

v ( о ) = v о ; v '( о ) = ф ( о ) = Ф о ; v ( L ) = V i ; v '( L ) = ф ( L ) = ^ .

Штрихом в (4) обозначена производная функции v ( x ) по x .

Из формул (3) следует, что классические функции формы не учитывают закон распределения изгибной жест- кости по длине элемента, что, в свою очередь, негативно сказывается на точности получаемых результатов расчета. Для повышения точности расчетов, при использовании вариационной постановки задачи, может быть применен метод двойной аппроксимации [20].

Изгибающий момент связан с кривизной соотношением:

d2vM

---— —.

dx 2

Здесь D z — изгибная жесткость поперечного сечения балки согласно (1).

С учетом (2) и (3):

Mz (12 x   6 1     (6 x4

— V — +ф -+

Dz    о к L3   L2 J     к L2

—

12 x 6 1

7г⁺F ]^{+ф 1}

( 6 x 21 -- —- к L2 L J

Потенциальная энергия деформации изгиба определяется формулой:

L

^U = 2 J D z

d ² v I j —у I dx. dx )

С учетом (6) и (1) формула (7) примет вид:

U ■ ² L ³ /D о = 6 (v о +V 1 ) f 11 ^{+ 4 L} ( ² V о +V 1 ) f .2 ^{— 12} ( V о ⁺ V 1 ) f 13 ^{+ 4 L} ( V о ^{+ 2} V 1 ) f 14 ⁺

^{+ L 2} ( 3 V о +V 1 ) f 22 ^{— 4 L} ( ² V о +V 1 ) f 23 ^{+ 2 L 2} ( V о +V 1 ) f 24 ^{+                         (8)}

^{+ 6} ( V о ⁺ V 1 ) f 33 ^{— 4 L} ( V о ^{+ 2} V 1 ) f 34 ^{+ L 2} ( V о ⁺ 3 V 1 ) f 44 ,

где fii = vоvо; f2 = vоФо; fi3 = vоvi; f.4 = vоФ1;(9)

f 22 = Ф о ф 0 ; ^f 23 = Ф о v 1 ; ^f 24 = Ф о Ф 1 / f 33 = v 1 v 1 >' ^f 34 = v 1 Ф 1 >' ^f 44 = Ф 1 Ф 1 ■

Если ввести вектор неизвестных U = [ v _о , Ф _о , v₁, ф₁ ] T , то (8) можно переписать в следующем виде:

U = 1UT •[K]• и.(Ю)

Здесь [ K ] — матрица жесткости элемента, определенная с учетом (8) и (9):

[ к ] = ^	6 ( ф о + ф 1 )	2 L ( 2 ф о +Ф 1 )	- 6 ( ф о + Ф 1 )	2 L ( ф о + 2 ф 1 )	■                       (11)
	2 L ( 2 ф о + ф 1 )	L 2 ( 3 Ф о + Ф 1 )	- 2 L ( 2 ф о +ф 1 )	L 2 ( ф о + ф 1 )
	- 6 ( ф о +Ф 1 )	- 2 L ( 2 ф о +Ф 1 )	6 ( ф о + ф 1 )	- 2 L ( ф о + 2 ф 1 )
	2 L ( ф о + 2 ф 1 )	L 2 ( ф о +Ф 1 )	- 2 L ( ф о + 2 ф 1 )	L 2 ( ф о + 3 ф 1 )

Случай ^о = ^о = 1 соответствует классической матрице жесткости балки.

Положительные направления узловых нагрузок X i и внутренних усилий приведены на рис. 2 б , из которого следует:

Qо = -X1; Mо = X2; Q1 = X3 ;M1 =-X4.(12)

Вычислим работу внешних сил.

L

W = X1 vо + X2фо + X3v1 + X4ф1 + I (qv) dx = qL ^    (     qL2

X +     v^ + X ₂ +

¹    2 I ^о I ²    12

о            п фо +^ X з + “2 |v 1 + 1 X 4- q2 ]ф1 ■

В матричной форме:

W = uT •(F + Fq),(14)

где F — вектор сосредоточенных узловых нагрузок; F q — вектор узловых нагрузок от распределенных. Компоненты данных векторов имеют вид (15):

F = [ X1, X 2, X 3, X 4 ] T; Fq = [ qL/2, qL2 /12, qL/2, - qL2 /12] T.(15)

Как видим, полученный в (15) вектор узловых усилий от распределенных нагрузок не учитывает изменение жесткости по длине. Это является недостатком вариационного подхода в контексте рассматриваемой задачи.

Полная энергия системы с учетом (Ю) и (14) определяется выражением:

П = U - W = 1UT •[ K ]• U - UT •( F + Fq).(16)

Применяя принцип минимума потенциальной энергии, получим условие стационарности функционала (16):

— = -(1UT •[K]• U-UT • (F + Fq В = [K]• U-FF + Fq) = о. ди    дu I 2

Из (17) следует основное уравнение метода конечных элементов: [ к ] • u = F + F_q.

Прямой метод получения матрицы жесткости. Полученная матрица жесткости (11) обладает существенным недостатком. Если принять v _о = ф_о = о, а также ^_о = о и ^₁ = 1 (что соответствует нулевой жесткости на левом защемленном краю), момент на левом краю будет определяться формулой:

M о = ^X 2 = ^K 2 , 1 v о ^{+ K} 2 , 2 ^ф о ^{+ K} 2 , 3 v 1 ^{+ K} 2 , 4 ^ф 1 = l ₂ ( ² v 1 ^{+ ф} 1 ^L ) ■

Отметим, что в (19) рассматривается предельный случай — математическая идеализация, когда жесткость на опоре не просто мала, а асимптотически стремится к нулю. Таким образом, в соответствии с (19), момент на левом краю не обращается в ноль, что противоречит формуле (5). Причина заключается в неточной аппроксимации функции прогибов формулой (2). Чтобы устранить это несоответствие, была найдена точная матрица жесткости путём непосредственного интегрирования дифференциального уравнения изгиба балки с учётом изменения жесткости по длине по формуле (1).

Механика

Аналогичный подход применяли и другие авторы. В работе [21] решение получено в форме степенных рядов, поэтому его нельзя считать замкнутым. В работе [22] методом непосредственного интегрирования получена матрица жесткости элемента со степенным законом изменения жесткости для задач устойчивости. В работе [23] рассматривался произвольный закон изменения жесткости по длине, однако для практического использования представленных результатов требуется выполнить интегрирование. Работы [24, 25] посвящены решению задач устойчивости. В этих работах закон изменения жесткости по длине задан в виде полинома второй и четвёртой степени, при этом не приведён вектор узловых сил от распределённых нагрузок. Общим недостатком работ, учитывающих полиномы второй и более высокого порядков в функции изменения жесткости по длине, является сложность вычисления матрицы жесткости. Так, например, для получения коэффициентов матрицы жесткости согласно [26] необходимо вычислять выражения вида sin [ε ln (λ)] (сохранены исходные обозначения), что затрудняет анализ предельных случаев и внедрение решений в коммерческие программные комплексы.

Для получения точной матрицы жесткости рассматривается известное из курса сопротивления материалов дифференциальное уравнение плоского поперечного изгиба балки с переменной жесткостью:

d ² ( D d ² v ]_ dx ² 1 z dx ² J q

Учитывая вид (1), общее решение однородного уравнения (20) будет содержать логарифм. Исключим размерные величины под знаком логарифма путем замены переменной по формуле:

x = pL, 0 > p > 1.

• (21)

• (22)

• (23)

Учитывая (21): dv 1 dv Ф =— =-- .

dx L d p

В результате общее решение уравнения (20) примет вид [27]: v(p) _ C 1 + C2 (p —a)2 + C3 (p-a) + C4 (p —a)In|p — a| + v*, где α = ψ0 / (ψ0 – ψ1); v* — частное решение неоднородного уравнения. Ввиду громоздкости частное решение не приведено.

Решение (23) справедливо для случаев ψ 0 ≠ ψ 1 , ρ ≠ α, так как эти случаи порождают неопределенности, которые будут раскрыты предельным переходом в формулах (31), (32) и (33).

Неизвестные константы интегрирования определяются из граничных условий:

v ( 0 ) _ v 0 ; v '( о ) = Ф о L; v ( 1 ) _ v I ; v '( 1 ) = Ф 1 L.                                      (24)

В (24) штрихом обозначена производная по ρ. Множитель L у углов поворота в граничных условия (24) присутствует из-за введенной замены переменной (21), что отражено в (22). После определения констант интегрирования из (24), момент и поперечная сила в балке, с учетом введенной замены переменных, вычисляются по формулам:

M _ —

D о [v о +p(Vi — У о)] d2 v (p)

(

L ²

d p2

; Q _— 4d- dо [vо + p(v L d p

\

d2v(p)^ ''1—v 0 >] -d?- J

Коэффициенты матрицы жесткости с учетом (25) и (12) могут быть найдены из выражений:

X 1 ^{_ —} Q ( ^о ) ^_ k 11 V о ⁺ k 12 ф о ⁺ k 13 V 1 ⁺ k 14 Ф 1 ^— F q, 1 ;

X 2 _ M ( о ) _ k 21 V о + k 22 ф о + k 23 V 1 + k 24 Ф 1 - F q,2 ;

> .

X 3 ^_ Q ( ¹ ) ^{_ k} 31 ^v о ^{+ k} 32 ^ф о ^{+ k} 33 ^v 1 ^{+ k} 34 ^ф 1 ^{— F}q, 3 ^;

X 4 ^{_ —} M ( ¹ ) ^_ k 41 v о ^{+ k} 42 ^ф о ^{+ k} 43 ^v 1 ^{+ k} 44 ^ф 1 ^— F q, 4 ■

Матричная форма (26) эквивалентна полученной ранее (18). Матрица жесткости в рассматриваемом случае

примет вид:

[ K ]_ Dr в L3

2 ^ 2 X	2 L ^й о	— 2 ^ 2 X	— 2 L ^и 1
2 L ^ш о	L 2 (2 v о © о — ^ 2 )	— 2 L ^и о	— L 2 (2 v о © 1 + ^ 2)
— 2 ^ 2 X	— 2 L ^й о	2 ^ 2 X	2 L
— 2 L ^© 1	— L 2 (2 v о © 1 +^ 2 )	2 L ^	L 2 (2 ф 1 © 1 +^ 2)

В (27) для компактности введены следующие обозначения:

^_in(vо/vi); ^ = vо —vi; ₽ = ^(vо+vi)—2^; ©о = vо^ —^; ©1 =vA —^.

Для реализации предлагаемой матрицы жесткости в программном обеспечении критически важно иметь возможность преобразования распределенных нагрузок в вектор узловых сил. Ниже записаны точные выражения вектора F q .

F q =	qL _ 2 А. (2 у 2 + 2 у 0 у 1 -у 2 ) - 3 ^ ( 3 у 0 -у 1 ) ]	.                                     (29)
	6^ qL 2 [ 2 Ху 0 ( у 0 + 2 у 1 ) -£ ( 5 у 0 + у 1 ) ] 12 ₽^ qL [ 2 1 ( у 0 - 2 у 0 У 1 - 2 у 2 ) - 3 ^ ( у 0 - 3 у 1 ) ]
	qL 2 [ 2 Ху 1 ( 2 у 0 + у 1 ) - ^ ( у 0 + 5 у 1 ) ] [                     12 ₽^                    ]

Основным достоинством полученных матрицы (27) и вектора (29) является простота реализации, а также отсутствие в вычислениях рядов и специальных функций.

При решении некоторых задач коэффициенты жесткости сечения у₀ и у 1 удобнее связывать с кривизной. В этом случае необходимо знать, каким образом кривизна связана с перемещениями и углами поворота узлов элемента. Для этого можно воспользоваться формулой (5). Зная, каким образом момент выражается в начале и конце элемента согласно формулам (26), получим:

d 2 v dx 2   0 x =0 d 2 v dx 2 x = L

= n     ( k 21 v 0 + k 22 ^ 0 + k 23 v 1 + k 24 ^ 1   Fq, 2 ) ’ D z ( 0 )    4D 0 у 0                                           l                      (30) m (p = 1)      1 /                                    \ -               = гл    ( k 41 v 0 + k 42 ^ 0 + k 43 v 1 + k 44 ^ 1   Fq, 4 ) ' D z ( x = L )   D 0у1

Случаи у₀ = 0, у 1 = 0 и у₀ = у 1 = у порождают неопределенности различного вида в матрице (27) и векторе (29).

Раскроем их.

Случай у0 = 0.

[ K ] =2T	■ 1	0	- 1	L ’	Г qL/ 3 " 0 ; F q = 9         .                                 (31) 2 qL / 3 _- qL 2 / 6 ]
	0	0	0	0
	- 1	0	1	- L
	_ L	0	- L	L 2 _

Случай у 1 = 0.

[ K ] = 2 ^^	Г и	L	- 1	0 "	Г 2 qL/ 3~ -    qL 2 / 6 ; F q =   J,,.                              (32) qL/ 3 [ 0 ]
	L	L 2	- L	0
	- 1	- L	1	0
	[ 0	0	0	0 ]

Из (31) и (32) видно, что столбцы и строки матрицы жёсткости, а также компоненты вектора узловых сил от распределённых нагрузок, связанные с изгибающими моментами на левом и правом концах конечного элемента соответственно, обратились в ноль — что соответствует уравнению (5). Обращение в ноль изгибной жёсткости может возникать, например, при обрыве растянутой арматуры или разрушении сжатой зоны железобетонной балки в каком-либо сечении. В случае статически неопределимой балки при подобных разрушениях конструкция может продолжить работу. В коммерческих программных комплексах при возникновении подобных ситуаций, как правило, в расчётной схеме активируются шарниры.

Случай у₀ = у 1 = у. Данный случай соответствует классической матрице жесткости.

[ K ] = Df	■ 12	6 L	- 12	6 L "	Г qL/ 2 "  - _ qL 2 / 12 ; F q = qL/ 2 [- qL 2 / 12 _
	6 L	4 L 2	- 6 L	2 L 2
	- 12	- 6 L	12	- 6 L
	_ 6 L	2 L 2	- 6 L	4 L 2 ]

Механика

В практических расчетах для снижения вычислительных погрешностей, которые могут накапливаться в процессе вычисления компонентов матрицы жесткости и множителей (28), рекомендуется принимать формулы (31), (32) и (33) не при строгом достижении предельного случая, а при приближении к нему. Например, установить пороговые условия для использования (27) и (29) в виде у i > 10^-4 и |1 - у₀ / у 1 | > 10^-3 . Указанные значения ориентировочные и зависят от особенностей конкретной реализации.

На рис. 3 приведены графики трех элементов матрицы жесткости, рассчитанные по формулам (11) и (27) при ψ 1 = D 0 = L = 1.

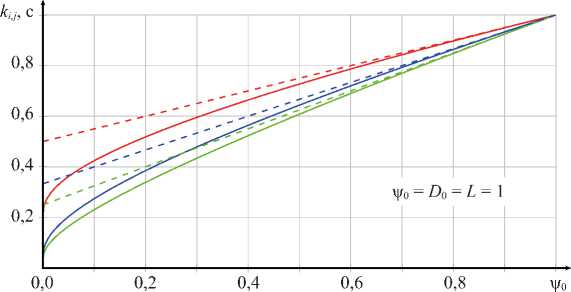
---к_и^т,,/12     ----A-₂₂™™74     ---A-_l2™‘76

---кц "P"™712     ---A-₂₂"P"^fo74     --- к, ₂"p"”76

Рис. 3. Зависимости k 11 , k 22 и k 12 от ψ 0 . Сплошные линии — на основе точной матрицы жесткости (27); пунктирные — на основе приближенной матрицы (11)

Из представленных на рис. 3 результатов видно, что при ψ 0 = 0 и соответствующих граничных условиях коэффициенты матрицы жёсткости, связанные с моментом на левом краю, в точной матрице (27) обращаются в ноль — это соответствует физическому смыслу. Приближённая матрица жёсткости (11) таким свойством не обладает. При существенной разнице жёсткости в начале и конце элемента (ψ 0 / ψ 1 < 0,2) значения коэффициентов точной и приближённой матриц могут различаться до 100 % (исключая из рассмотрения предельный случай ψ 0 → 0). В подобных ситуациях рекомендуется использовать точную матрицу жёсткости (27). Для правого края конечного элемента могут быть сделаны аналогичные выводы.

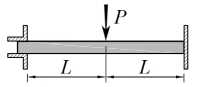
Результаты исследования. Для демонстрации результатов, полученных с использованием предложенных матриц жесткости, выполнены примеры расчета для балок длиной 2 L , изображенных на рис. 4.

а)

jllllllllllllllll!

б)

Рис. 4. Эскизы схем для примеров расчета:

а — защемленная балка длиной 2 L , нагруженная сосредоточенной силой; б — то же при действии равномерно-распределенной нагрузки

Ввиду симметрии относительно x = L, в решении рассматривается половина балки. Граничные условия при действии сосредоточенной силы (схема на рис. 4 а) приняты следующие:

v(0) = 0; v'(0) = 0; v'(L) = 0; (Dzv")'

- P/ 2 .

x = L

Аналогично для случая распределенной нагрузки (схема на рис. 4 б ): v ( 0 ) = 0 ; v '( 0 ) = 0 ; v '( L ) = 0 ; ( D z v ") '

= о .

x = L

Будет рассмотрена следующая функция распределения жесткости по длине балки:

D z ( x ) = D 0

s 0

—

x /                ч     2 x ² /

— ( 3 s 0 + s 1 ^— 4 ) + -2- ( s 0 + s 1 ^{— 2} ) .

L ²

s 0 и s 1 — коэффициенты к жесткости балки в начале и середине пролета, т.е. D z (0) = D 0 s 0 и D z ( L ) = D 0 s 1 .

При этом D z ( L / 2) = D 0 . Важно отметить, что (36) определяет закон изменения жесткости по длине балки в целом, в то время как (1) — по длине конечного элемента.

Функция (36) выбрана исходя из способа приложения нагрузки и граничных условий. Для балки постоянной жесткости в этом случае моменты на опоре и в середине балки будут достигать максимальных значений. В случае, если материал балки железобетон, в этих точках стоит ожидать образование трещин снижение изгибной жесткости [27] . В четверти пролета моменты близки к нулевым и, следовательно, жесткость близка к начальной D z ( L / 2) = D 0 .

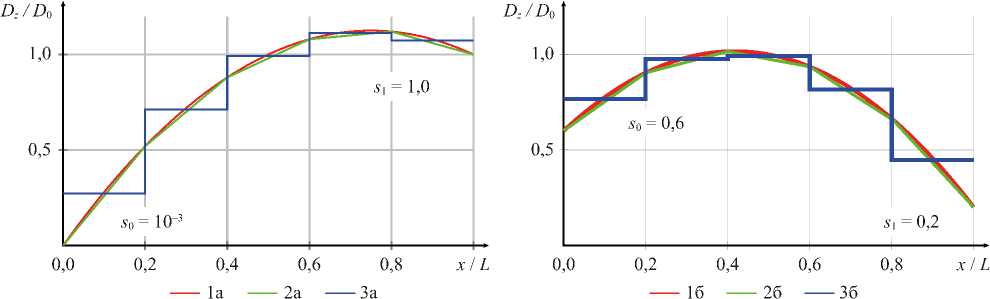
На рис. 5 представлены графики распределения жесткости по длине балки, а также рассматриваемые методы аппроксимации для двух вариантов: вариант 1 — s 0 = 0,001; s 1 = 1,0; вариант 2 — s 0 = 0,6; s 1 = 0,2.

а)

б)

Рис. 5. Распределение жесткости D z ( x ) / D о по длине балки: а — вариант 1 — s о = 0,001 и s 1 = 1,0; б — вариант 2 — s 0 = 0,6 и s 1 = 0,2. Кривые 1 а и 1 б — исходная функция; 2 а и 2 б — кусочно-линейная аппроксимация; 3 а и 3 б — дискретная аппроксимация

Из представленных на рис. 5 результатов видно, что линейная аппроксимация даже при пяти конечных элементах дает удовлетворительное совпадение (отклонение не превышает 5 %) с исходной функцией изменения жесткости по длине для рассматриваемых примеров. Высокая точность сохраняется при аппроксимации жесткости кусочно-линейной функцией для переменных сечений сложной формы [28] . Значение средней жесткости при дискретной аппроксимации вычислялось по формуле:

D zi =

x i + 1

^xi +1

—

x i

J Dz (x) d

xi

Результаты вычисления коэффициентов у для матриц жесткости конечных элементов приведены в таблице 1. Для дискретной аппроксимации у₀ = у 1 = у.

Коэффициенты матриц жесткости элементов

Таблица 1

Элемент		1		2		3		4		5
х ,	x i + 1	0,0	0,6	0,6	1,2	1,2	1,8	1,8	2,4	2,4	3,0
Вариант 1: s 0 = 0,001 и s 1 = 1,0
Коэфф. у о,1		у о	У 1	у о	у 1	у о	у 1	у о	у 1	у о	у 1
Линейная		0,001	0,52	0,52	0,88	0,88	1,08	1,08	1,12	1,12	1,0
Дискретная		0,274		0,714		0,993		1,113		1,073
Вариант 2: s 0 = 0,6 и s 1 = 0,2
Коэфф. у о,1		у о	У 1	у о	у 1	у о	у 1	у о	у 1	у о	у 1
Линейная		0,6	0,904	0,904	1,016	1,016	0,936	0,936	0,664	0,664	0,2
Дискретная		0,768		0,976		0,992		0,816		0,448

Так как решается упругая задача, результаты расчета компонентов напряженно-деформированного состояния линейно зависят от величины нагрузки и начальной жесткости D 0 . Ввиду этого в расчете данные величины приняты равными единице.

Механика

Решение уравнения (20) с граничными условиями (34) и законом изменения жесткости (36) найдено аналитически для рассматриваемых значений s ₀ и s 1 . Ввиду громоздкости данное решение здесь не приведено. Для произвольных значений s ₀ и s 1 аналитическое решение получить не удалось.

Результаты из полученного аналитического решения далее сравнивались с результатами расчета методом конечных элементов. В основном расчете балка была разбита на 5 конечных элементов. Для исследования влияния числа конечных элементов на точность результатов была выполнена серия расчетов, в которых варьировалось их количество.

По результатам проведённых расчётов определялась величина погрешности по сравнению с аналитическим решением. Для формулирования выводов о необходимом числе элементов принята пороговая погрешность 5 %. Выводы о возможности применения подхода в практических расчётах формировались из условия, что пороговая точность достигается при числе элементов меньше 60 — в этом случае длина конечного элемента составляет 50 мм. Применение более мелкого разбиения нецелесообразно для расчёта балок в строительных конструкциях — оно приводит к существенному увеличению вычислительных затрат и времени расчёта. Максимальное число элементов в примерах расчёта принималось равным 400 (длина конечного элемента при этом составляет 7,5 мм). При большем числе конечных элементов в реализованном автором решателе начинали накапливаться вычислительные ошибки.

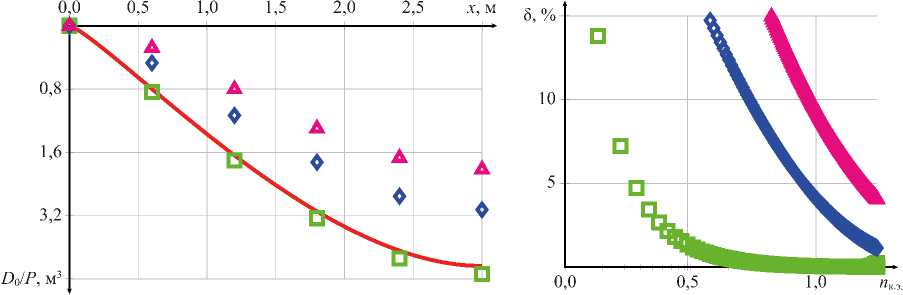
Пример 1. Решение задачи изгиба защемленной балки, нагруженной в центре сосредоточенной силой. Эскиз расчетной схемы приведен на рис. 4 а . Распределение жесткости принято по варианту 1: s 0 = 0,001 и s 1 = 1. График функции жесткости для данного варианта приведен на рис. 5 а . На рис. 6, 7 приведены результаты вычисления прогибов и изгибающих моментов, а также погрешность вычислений.

□ la ^2a АЗа ---4а                         □ 16 $26 АЗб

а)                                                                     б)

Рис. 6. Результаты вычисления прогибов для примера: а — результаты вычисления прогибов v в зависимости от x ; б — погрешность вычисления в зависимости от числа конечных элементов.

1 а , 1 б — линейная аппроксимация и точная матрица жесткости (27);

2 а , 2 б — линейная аппроксимация и приближенная матрица жесткости (11);

3 а , 3 б — дискретная аппроксимация; 4 а — результаты аналитического расчета

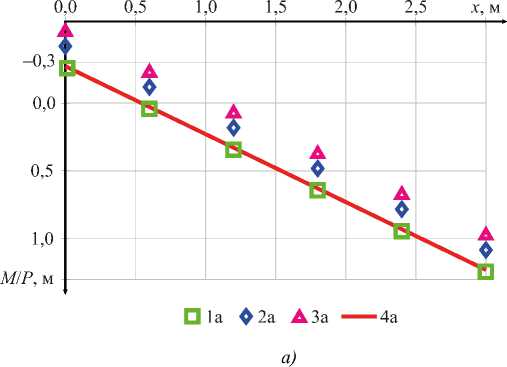
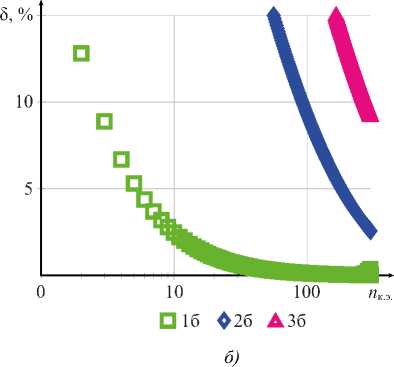
Рис. 7. Результаты вычисления моментов для примера 1:

а — результаты вычисления изгибающих моментов M в зависимости от x ; б — погрешность вычисления в зависимости от числа конечных элементов; 1 а , 1 б — линейная аппроксимация и точная матрица жесткости (27);

2 а , 2 б — линейная аппроксимация и приближенная матрица жесткости (11); 3 а , 3 б — дискретная аппроксимация;

4 а — результаты аналитического расчета

Пример 2. Рассмотренный ранее пример 1 представляет собой случай, близкий к предельному, так как жесткость на левом краю балки стремится к нулю. Для более объективной оценки точности рассматриваемых подходов выполнена аналогичная серия расчетов для случая плавного изменения жесткости. На рис. 8, 9 представлены результаты для варианта 2 изменения жесткости, а именно для s 0 = 0,6 и s 1 = 0,2. График функции жесткости для данного варианта приведен на рис. 5 б .

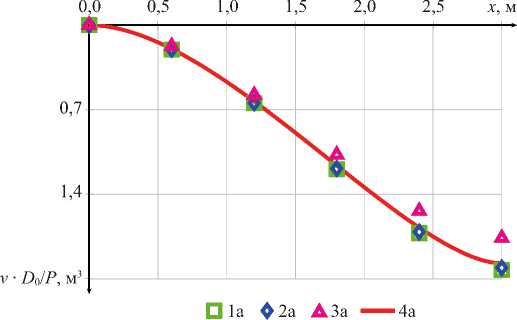
а)

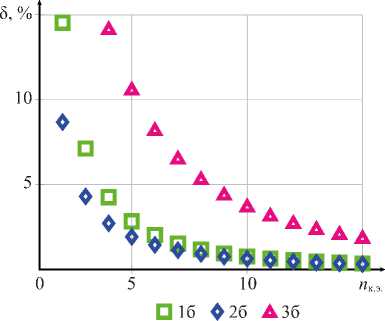
б)

Рис. 8. Результаты вычисления прогибов для примера 2: а — результаты вычисления прогибов v в зависимости от x ;

б — погрешность вычисления в зависимости от числа конечных элементов. 1 а , 1 б — линейная аппроксимация и точная матрица жесткости (27); 2 а , 2 б — линейная аппроксимация и приближенная матрица жесткости (11); 3 а , 3 б — дискретная аппроксимация; 4 а — результаты аналитического расчета

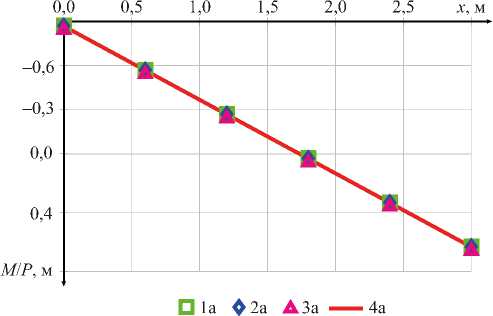
а)

Рис. 9. Результаты вычисления моментов для примера 2: а — результаты вычисления изгибающих моментов M в зависимости от x ; б — погрешность вычисления в зависимости от числа конечных элементов; 1 а , 1 б — линейная аппроксимация и точная матрица жесткости (27); 2 а , 2 б — линейная аппроксимация и приближенная матрица жесткости (11);

3 а , 3 б — дискретная аппроксимация; 4 а — результаты аналитического расчета

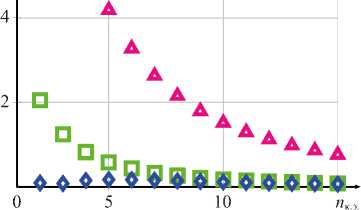
□ 16 ^26 АЗб

б)

Пример 3. Задача изгиба защемленной балки, находящейся под действием распределенной нагрузки. Эскиз приведен на рис. 4 б . Результаты расчета на рис. 10, 11 получены для варианта 1 распределения жесткости, т.е. для s 0 = 0,001 и s 1 = 1.

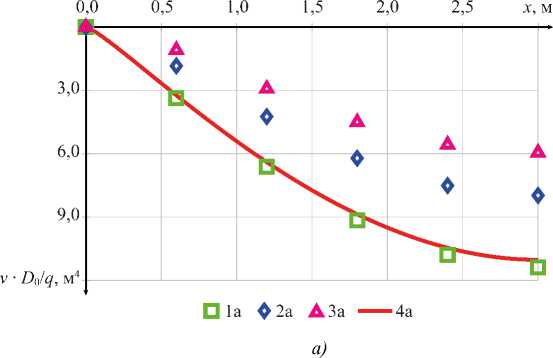
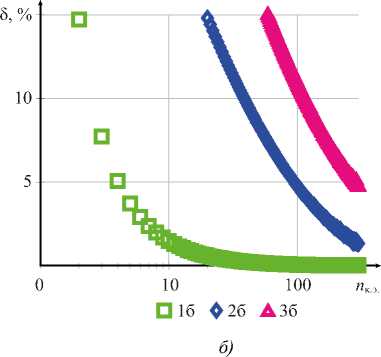
Рис. 10. Результаты вычисления прогибов для примера 3: а — результаты вычисления прогибов v в зависимости от x ; б — погрешность вычисления в зависимости от числа конечных элементов; 1 а , 1 б — линейная аппроксимация и точная матрица жесткости (27); 2 а , 2 б — линейная аппроксимация и приближенная матрица жесткости (11);

3 а , 3 б — дискретная аппроксимация; 4 а — результаты аналитического расчета

Механика

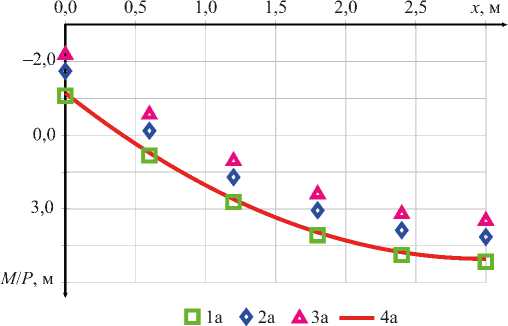
а)

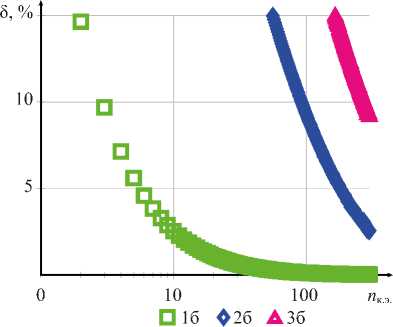
б)

Рис. 11. Результаты вычисления моментов для примера 3: а — результаты вычисления изгибающих моментов M в зависимости от x ; б — погрешность вычисления в зависимости от числа конечных элементов; 1 а , 1 б — линейная аппроксимация и точная матрица жесткости (27); 2 а , 2 б — линейная аппроксимация и приближенная матрица жесткости (11);

3 а , 3 б — дискретная аппроксимация; 4 а — результаты аналитического расчета

Обсуждение. На основе анализа результатов, приведённых на рис. 6 и 7, сформулированы следующие заключения. В случаях существенного изменения жёсткости, как в рассмотренном примере 1, только точная матрица жёсткости (27) позволяет получить результаты, сопоставимые с аналитическим расчётом. Пороговая точность в 5 % в этом случае достигается при 5 конечных элементах для перемещений (рис. 6 б ) и при 6 конечных элементах (рис. 7 б ) для изгибающих моментов. При использовании приближённой матрицы жёсткости (11) аналогичная точность достигается только при 90 и 180 конечных элементах для прогибов и моментов соответственно. Дискретная аппроксимация позволила достичь пороговой точности по прогибам при 220 конечных элементах. По моментам требуемая точность при дискретной аппроксимации не была достигнута даже при 400 элементах.

Результаты расчёта при действии распределённой нагрузки, приведённые на рис. 10 и 11 для примера 3, аналогичны приведённым на рис. 6 и 7 для примера 1. Основным отличием является то, что точность результатов при использовании приближённой матрицы (11) и при дискретной аппроксимации уменьшилась. Таким образом, можно сделать вывод, что на результаты расчёта влияет не только матрица жёсткости — точная или приближённая — но и вектор узло- вых сил от распределённых нагрузок.

По результатам расчёта при плавном изменении жёсткости, приведённым на рис. 8 и 9 для примера 2, сфор-

мулированы следующие выводы. Приближённая (11) и точная матрица жёсткости (27) конечного элемента в случае плавного изменения жёсткости балки по длине позволяют получить сопоставимые по точности результаты при меньшем числе элементов. Например, для достижения погрешности в 5 % при вычислении прогибов при использовании предложенных матриц требуется не более 4 конечных элементов против 8 при дискретной аппроксимации. Таким образом, даже в случае плавного изменения жёсткости линейная аппроксимация в пределах конечного элемента позволяет снизить степень дискретизации расчётной схемы в два раза, сохраняя сопоставимую точность расчёта.

Представленные на рис. 8 б и рис. 9 б результаты имеют особенность. Результаты, полученные с использованием приближённой матрицы жёсткости (11) при одинаковом числе элементов, показывают меньшее отклонение от аналитического решения, чем результаты, полученные с использованием точной матрицы (27). Причиной этого является выпуклость (рис. 5) функции изменения жёсткости по длине. В этом случае площадь фигуры, ограниченная сверху аппроксимацией, меньше, чем исходная. Следовательно, величина прогибов, полученная с использованием линейной аппроксимации, оказывается больше (0 а). Из результатов расчета коэффициентов приближенной (11) и точной матрицы (27), приведенных на рис. 3, видно, что приближенная матрица (11) обладает большей жесткостью, что частично компенсирует данный эффект и снижает общую погрешность. Ниже приведена матрица [А Х ], коэффициенты которой вычислены по формуле A K i,j = К Лр^иб' / К о ^чн' где К ^риб. — коэффициенты матрицы (11); Кто^чн' — коэффициенты матрицы (27). Вычисления выполнены для параметров у₀ = 0,664, y 1 = 0,2, D ₀ = 1,0 и L = 0,6, что соответствует пятому конечному элементу для варианта 2 распределения жесткости.

[АК ] =

1 , 09

1 , 08

1 , 09

1 , 11

1 , 08

1 , 06

1 , 08

1 , 14

1 , 09

1 , 08

1 , 09

1 , 11

1 , 11

1 , 14

1 , 11

1 , 09

Среднее значение коэффициентов матрицы (38) составляет 1,098. Следовательно, жесткость конечного элемента 5 будет ориентировочно на 10 % выше, если используется приближенная матрица жесткости (11).

Заключение. В работе предложен и верифицирован подход к построению матриц жесткости для балочных конечных элементов с линейным изменением жесткости по длине. Получены как приближённая (на основе вариационного решения задачи), так и точная (путём аналитического интегрирования дифференциального уравнения) матрицы жесткости и соответствующие векторы узловых нагрузок. Ключевыми преимуществами полученных матриц являются следующие:

• 1.    Аналитический вид приближённой (11) и точной (27) матриц жесткости, а также приближённого (15) и точного (29) вектора узловых сил от распределённых нагрузок, что делает их легко внедряемыми в существующие МКЭ-программы — как в авторской реализации на Python, так и в коммерческих пакетах.

• 2.    Представленные примеры верификации (рис. 6–11) позволяют утверждать, что даже при сравнительно грубой дискретизации (небольшое число элементов) линейная аппроксимация адекватно описывает напряжённо-деформированное состояние балок как при плавном, так и при резком изменении жесткости (включая моделирование зон существенного падения жесткости).

Линейная аппроксимация жёсткости обеспечивает оптимальное соотношение точность – сложность – вычислительные ресурсы, делая предложенный метод практичным инструментом для анализа реальных конструкций переменной жёсткости. Сравнение результатов расчёта с использованием приближённой и точной матрицы жесткости показывает, что приближённая матрица позволяет с высокой точностью и при меньших вычислительных затратах обеспечить требуемую точность для балок с плавным изменением жесткости по длине. При быстром изменении жесткости по длине, а также в предельных случаях для достижения существенно более высокой точности при сохранении числа элементов рекомендуется использовать точную (27) матрицу жесткости. Дискретная аппроксимация применима лишь в случаях плавного изменения жесткости по длине.

Полученные матрицы жесткости открывают возможности для более точного и эффективного анализа реальных конструкций, в том числе железобетонных элементов с учётом физической нелинейности — это определяет направление дальнейших исследований. Также предполагается получение геометрической матрицы жесткости для решения задач устойчивости и матрицы масс для динамического анализа.

Sventikov AA, Kuznetsov DN. Strength and Deformability of Steel Beams with a Step-by-Step Change in Wall Thickness. Russian Journal of Building Construction and Architecture. 2025;1(77):14–23.

Yagofarov AKh. Calculation of a Two-Span Uncut Beam of Variable Rigidity with Equal Spans. News of Higher Educational Institutions. Construction. 2021;(754(10)):55–65.

Karamysheva AA, Yazyeva SB, Chepurnenko AS. Calculation of Plane Bending Stability of Beams with Variable Stiffness. Bulletin of Higher Educational Institutions. North Caucasus region. Technical Sciences. 2016;(186(1)):95–98.

Cherednichenko AP, Potelzheko EA, Tyufanov VA. Methods for Calculating Beams with Variable Stiffness. In: Proc. International Student Construction Forum-2017. Vol. 1. Belgorod: Belgorod State Technological University named after V.G. Shukhov; 2017. P. 249–252.

Nesterov VA. Stiffness Matrix of the Tridimensional Beam Finite Element with Low Transverse Shear Stiffness. Siberian Aerospace Journal . 2010;29(3):71–75.

Fedorinin NI, Solomonov KN, Tishchuk LI. Universal Equation of Elastic Line of a Beam of Linear Rigidity. News of Tula State University. Technical Sciences. 2022;(9):517–521.

Об авторе: