Точное решение одного функционально-дифференциального уравнения параболического типа с помощью теории полугрупп и некоторые его применения

Функционально-дифференциальные уравнения параболического типа активно используются при решении целого ряда задач оптоэлектроники [1] и математической биологии [2]. Многие общие свойства уравнений такого типа описаны в обзоре [3]. Однако в математической физике важную роль играют не только свойства решений её уравнений, но и построение точных решений этих последних, поэтому рассмотрим задачу Коши на прямой: d u ( x , t )     d ² u ( x , t )         ,     .       _{z           z 4}                        c

--------=----- j+ a • u ( - x , t ) ,    u ( x ,0) = u ₀( x ) , x e R , a ^ 0.            (1) d t         d x ²

Для этой задачи справедлива следующая теорема.

Теорема. Пусть u ₀ е L _w ( R ) , тогда точное решение задачи Коши (1) имеет вид:

+w u (x, t) = j g(x, %; t) ■ u0% • d% ,

-w где интегральное ядро оператора эволюции равно g (x ,%; t) = ch (a ■ t) ■ G (x - %; t) + sh (a ■ t) ■ G (x + %; t) ,

а

G ( x ; t) =

2 ■ V n ■ t

• exp ■ x

2 A x

4 • t)

Доказательство. Перепишем задачу Коши (1) для исходного функциональнодифференциального уравнения параболического типа в операторном виде:

u^- = Au,      u (0) = u ₀,                                  (5)

dt где

A = D ² + a ■ P                                   (6)

— линейный оператор, действие которого на произвольную функцию f ( x ) можно определить с помощью следующих правил: ( Df )( x ) = f '( x ) (оператор дифференцирования)

и ( Pf )( x ) = f ( - x ) .

Как хорошо известно [4], решение абстрактной задачи Коши (5) равно:

u ( t ) = exp( At ) u ₀.

Далее, входящий в формулу (6) оператор P есть не что иное, как широко используемый в квантовой механике оператор пространственной инверсии [5].

Этот оператор коммутирует с квадратом оператора дифференцирования D : [ D ², P ] = 0, следовательно:

exp[(D2 + aP) ■ t ] = exp(a ■ t ■ P) ■ exp(t ■ D2).                         (8)

Легко убедиться в том, что в пространстве L _w ( R ) оператор инверсии P ограничен, причём || P || = 1, поэтому:

w пП.П

exp( a ■ t ■ P ) = 2—- ■ Pⁿ . n = 0 n ^!

Но так как P ² = I , где I — тождественный оператор [5], то формула (9) упрощается:

exp( a ■ t ■ P ) = ch ( a ■ t ) ■ I + sh ( a ■ t ) ■ P .

Наконец, {exp(Z • D2)}>0 — оператор полугруппы Гаусса-Вейерштрасса, действие которого на произвольную функцию f е Lю (R) задаётся её свёрткой с функцией (4) [6]:

+∞

(exp( t • D ²) • f )( x ) = J G ( x - f ; t ) • f ( f ) • d f .

-∞

Комбинируя формулы (7), (8), (10) и (11), придём к выражениям (2) и (3), то есть к условию теоремы.

Теорема полностью доказана.

Интегрируя соотношение (2) по x по всей прямой и переставляя затем порядки интегрирования по x и по ξ , получим следующее утверждение.

Следствие 1. Если u ( x , t ) — точное решение задачи Коши (1) с начальным условием и ₀ е L 1 ( R ) , то:

+∞+∞

J и (x, t) • dx = exp(a • t) • J и 0( x) • dx.(12)

-∞-∞

Соотношение (12) демонстрирует разницу между поведением решений обычного уравнения параболического типа (a = 0) и функционально-дифференциального уравнения параболического типа ( а ^ 0), а именно, площадь, ограниченная решением уравнения (1) и осью x, со временем либо экспоненциально растёт (при а > 0), либо экспоненциально убывает (при а < 0) — в отличие от площади, ограниченной решением уравнения диффузии-теплопроводности ( а = 0), которая не меняется со временем.

Переходя в формуле (10) от гиперболических функций к экспоненциальным и используя затем формулу (8), легко вывести ещё одно следствие из доказанной выше теоремы.

Следствие 2. Оператор полугруппы, соответствующий инфинитезимальному генератору полугруппы (6), можно представить в виде:

exp( At) = [exp(a • t) • P+ + exp(-a • t) • P- ] • exp(t • D2),                  (13)

где P± = (I ± P)/2 — операторы, удовлетворяющие соотношениям P±2 = P±, то есть проекционные операторы.

Это представление эволюционного оператора задачи Коши (1) позволяет лучше понять общую структуру её точного решения (2), а именно, действуя согласно формуле (7) на начальное условие и ₀( x ) оператором полугруппы в представлении (13), получим, что:

и (x, t) = exp(a • t) • и+(x, t) + exp(-a • t) • и (x, t),

где u± (x, t) = (u0(x, t) ± u0(—x, t))/2 — соответственно чётная и нечётная части от функции u 0( x, t) = (exp(t ■ D 2)u0 )(x), являющейся решением обычного уравнения теплопроводности с тем же начальным условием u0 (x). Таким образом, из выражения (14) следует, что на больших временах при а > 0 остаётся и экспоненциально растёт чётная часть u+(x, t) от функции u0(x, t) , а при а < 0 остаётся и экспоненциально растёт нечётная часть u- (x, t) от функции u0 (x, t) .

Важной характеристикой инфинитезимального генератора (6) рассматриваемой полугруппы является его резольвента R _A ( A ) = ( A — A I ) ^{— 1} [4, 6].

Пусть функция r ( x , J ; A) — интегральное ядро оператора резольвенты. Оно действует на произвольный вектор f е L _ю ( R ) следующим образом:

+∞

( R a ( A ) f )( x ) = J r ( x , J A ) ■ f ( J ) ■ d J .

-∞

Применив к выражениям (2)-(4) формулу связи между оператором резольвенты и оператором полугруппы [4, 6]:

+∞

⁽ R A ( ^A ) f ⁾⁽ x ) = - J ^exP( - ^A ■ t ) ■ (^exP( ^At ) ^{f )( x} ) ■ ^{dt                        (16)}

и сравнив между собой выражения (15) и (16) после использования известных свойств преобразования Лапласа [7] и известного выражения интегрального ядра для резольвенты R _A ( D²) оператора D ² [6], несложно получить ещё одно утверждение.

Следствие 3. Интегральное ядро оператора резольвенты инфинитезимального генератора полугруппы (6) равно:

r ( x f ; A ) =

p ( x , J ; A — а ) + p ( x , — J ; A — а ) + p ( x , J ; A + а ) — p ( x , — J ; A + а ) 2

где p(x, J; A) = — exp(—JA- | x — J |)/(2 ■ VA) — интегральное ядро резольвенты RA(D2).

С другой стороны, подстановка представления (13) оператора рассматриваемой полугруппы в формулу (16) позволяет переписать выражение для резольвенты в операторном виде:

Ra( D2 + а ■ P) = P+ ■ RA—а (D2) + P— ■ Ra+« (D2).

Очевидно, что формулы (17) и (18) эквивалентны друг другу.

Рассмотрим пример точного решения задачи Коши (1). Выберем её начальное условие в виде гауссоиды с характерной шириной l0 , сдвинутой относительно начала координат на расстояние x :

u 0 ⁽ x ) = exp

⁽ x - x 0 ) 2

⁴ l 0

Оператор полугруппы Гаусса-Вейерштрасса (exp(D2t))  трансформирует во времени функцию (19) следующим образом:

u ⁰( x , t ) =

l

0 exp l0 + t

1 ( x — x 0 ) 4   1 ₀ 2 + 1

.

Наконец, из функции (20) по формуле (14) получаем точное решение задачи Коши (1)

с начальным условием (19):

u ( x , t) =

l0

T i F+ t

(

• ch( a t ) ■ exp

I

1 ( ^{x — x} 0 ⁾² 4    1 02 + 1

+ sh( a t ) • exp

—

¹ ( ^x + ^x 0 ⁾²

4   1 2 + 1

J

Графики функции (21) при x ₀ = 2 , l ₀ = 1 и различных значениях а приведены на рис.

1 и 2.

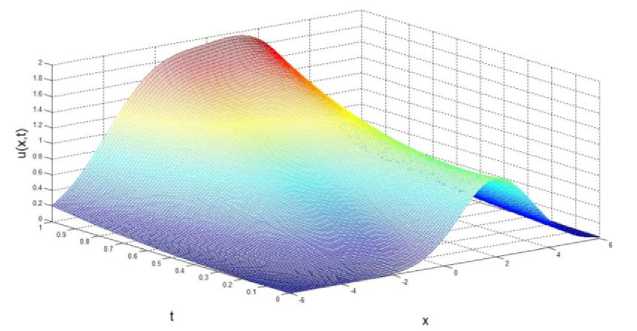
Рис. 1. Временная эволюция смещённой гауссоиды при а = 1,5.

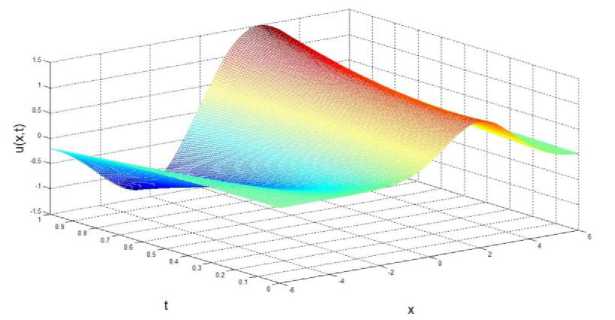
Рис. 2. Временная эволюция смещённой гауссоиды при а = — 1,5.

Из рисунка 1 видно, что на больших временах экспоненциально растёт чётная часть гауссоиды (20). Из рисунка 2 видно, что на больших временах экспоненциально растёт её нечётная часть. Таким образом, этот пример полностью иллюстрирует доказанную в данной работе теорему.

В заключение необходимо отметить, что полученные результаты могут быть применены для дальнейшего развития теории полугрупп, в частности, построенное точное решение задачи Коши (1) может быть положено в основу различных схем теории возмущений, а найденное в следствии 3 теоремы интегральное ядро оператора резольвенты инфинитезимального генератора полугруппы (6) даёт возможность вычислить резольвенты последовательных степеней этого оператора.