Точное решение уравнений Навье - Стокса, описывающее закрученные торнадообразные течения вязкого газа

Точные решения уравнений Навье - Стокса для сжимаемого вязкого газа крайне редки и представляют большой интерес, поскольку именно изучение точных решений дает правильное представление об основах гидромеханики. В случае несжимаемой вязкой жидкости известен ряд точных решений, когда исходную систему уравнений в частных производных удается свести к обыкновенным дифференциальным уравнениям, а в некоторых случаях даже решить задачу аналитически до конца. Особое место в этом ряду занимают точное решение Бюргерса, описывающее стационарное вихревое течение вязкой жидкости с тремя ненулевыми компонентами скорости [1], и решение Джеффри - Гамеля для течения вязкой несжимаемой жидкости в плоском диффузоре [2].

Впервые автомодельные решения уравнений Навье - Стокса для течения вязкого сжимаемого газа от источника массы в плоских и осесимметричных конических диффузорах

(с) Врутяп М. А., Ибрагимов У. Г., 2024

• (с) Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (национальный исследовательский университет)», 2024

2.    Постановка задачи

теоретически изучались в работах [3-6]. В [3] рассматривается осесимметричное течение в конусе с непроницаемыми стенками и условием скольжения для скорости и температуры на стенке. В [4-6] изучается течение в осесимметричных и плоских каналах с массоотводом газа на стенке. В работах [7, 8] рассмотрено течение в клине при условии адиабатической стенки и показано, что автомодельные решения, удовлетворяющие условию сплошной среды, реализуются в каналах с малыми углами раствора. В работе [8] найдены аналитические решения для течения в плоском канале с коэффициентами динамической вязкости и теплопроводности, зависящими от температуры по степенному закону, а в работе [9] рассмотрено аналогичное автомодельное течение вязкого сжимаемого газа от струи (источника импульса), истекающей в область между двумя расходящимися стенками. В недавних работах [Ю,П] получены новые автомодельные решения для течения вязкого газа при произвольной зависимости коэффициентов переноса от температуры, а в [11] найдены несимметричные автомодельные решения.

В работе [12] изучен новый класс автомодельных решений, в которых все параметры течения вдоль оси канала изменяются по экспоненциальному закону. При этом было изучено течение в ограниченной области, а именно в цилиндрическом канале.

Закрученные течения вязкого газа рассмотрены в работе [13]. Однако, как и в [12], автомодельные решения были получены только для ограниченной, на этот раз конической области, что не позволило авторам работы исследовать решения в дальнем поле.

В настоящей работе в предположении, что все параметры течения вдоль оси вихря изменяются по экспоненциальному закону, получено точное автомодельное решение уравнений Навье - Стокса для закрученного течения вязкого газа в неограниченной области. Система уравнений в частных производных при этом сводится к системе обыкновенных дифференциальных уравнений.

Полученные в настоящей работе автомодельные течения авторы не склонны отождествлять с реальной картиной течения в атмосферном торнадо [14]. Однако в отдельных аспектах найденные решения качественно напоминают эту картину.

Рассмотрим течение вязкого теплопроводного газа, закрученного вокруг некоторой оси. Введем цилиндрическую систему координат ( г, в, z) так, чтобы ось z совпадала с осью вращения газа: ж = г cos в, у = г sin в, z = z (рис. 1).

Рис. 1. Схема закрученного течения газа

Система уравнений Навье - Стокса в цилиндрических координатах имеет вид

1d         d raT(rpu) + al(pw) —°, (1) du dr du + - НЕ2 — - dp + 11. (rOrr) + A (Orz) - OH, r      dr r dr         dz         r (2) dv     dv pu^~ + Pw^~ dr     dz

+ ^p= = 11 (r^) + | ( o _>z ) + ^ , r dr        dz

г

r

dw dw dp 1d d (4) dr + '.■— - я—+ dz -^- (rOzr ) + r dr dz(Ozz), dh dh    dp    dp   1 d /  dT \

+1^)+ dz \ dz

Р dr  Р dz    dr    dz   r dr \  dr J

+ 2p {e_rr + e_ee + e _zz] + 4/z { е _гв + E_rz + e _0z) ^- -/z(divV) .

Здесь p, u, v, w, h, p — соответственно плотность, радиальная, азимутальная и продольная компоненты скорости, энтальпия и давления; р к — коэффициенты динамической вязкости и теплопроводности. Предполагается, что течение не зависит от азимутальной координаты в. Компоненты тензора напряжений ст:

(У rr

= 2pe_rr

-

- pdivV,   O ee — 2рЕ_вв

-

- pZ vV, 3

O zz

— ² p^ zz

-

- pdivV, 3

O re — O er — 2pE re ,  O rz — O zr — 2pE rz ,  O ze — O ez — 2pe ez ,

_ du _ u dw dz'

^rr —    , ^ee — ,   ^zz dr         r

_— 1 / dw  du \

2 dr + dz

_ 1 dv

^{£ez —} 2 dz^.

_ rd / v \

^{£re —} 2 drU,   ^£rz

Газ предполагается совершенным, подчиняющимся уравнению состояния:

p — pRT.

Введем безразмерные переменные, пусть r — rL, p — ppo, u — Uwo, v — vwo, w — Wwo, P — PPo> T — TTo, где переменные с индексом 0 берутся в некоторой точке на оси вихря. Компоненты вектора скорости отнесены к продольной компоненте скорости вдоль оси вихря wo; L — некоторый линейный размер вдоль оси вихря. Тогда система уравнений (1) - (5) примет следующий вид:

1 дд

... (rPu) + E^(Pw)— °.(6)

r drdz

__du^ du pv2 _ dp 1  (1 d_do pudU + pwdU - T — -dr + кД Ф dr(rOrr’+ du(Orz)- V f       (’ pu^+pw^ + pui —Д {1 » (rOer) + A (Oez) + Oer Г(SI dr dz r    Reo r dr        dzr

__dw   __dw     dp 1   1 d .. d pu~^ + l>w'    — -TX +     4 T3TZ (rOzr) + 3TX (Ozz)

dr dz     dz   Reo  r drdz ри дТ pw дТ _др _др (7 - 1) М2 д_ + (7 - 1)М2 дН = идг + W£)z +

,                     1

+ ( 7 - 1)5I0ReoPro

f 1 д Л_ дТ\   д __дT\^>\

[ г дг \д дг) + дг у dz) ) +

+² дд {^_2 г + ^£1 в + ^£zz } + 4 дд {^е^ ^{+ —} z + ^£l z } — о дд (^^vV) • Reo                   Reo                  3 Reo

Здесь Mo = wo/y/yRTo, Reo = poWoL/do, Pro = c_Pdo/^o ^— числа Маха, Рейнольдса и Прандтля соответственно; 7 = c_p/c_v — показатель адиабаты.

Автомодельное решение системы уравнений (6) - (10) будем искать в виде р = p(r)eaz, и = u(r)e^z, v = v(r)e^z, w = w(r)e^z,

T = T (r)e² ^ ^z, p = p(r)e^(a+2 ^ >^z , д = Tⁿ •

Нетрудно убедиться, что показатели степени вязких и конвективных членов совпадают при выполнении простого условия:

23п = a + /3.

Тогда исходная система уравнений в частных производных принимает форму обыкновенных дифференциальных уравнений:

¹ d

(И)

- — (rри) + 2nppw = 0, r dr рии' + pwu3 —

pv2 r

-P + lh т(гТП (4^ - 2 и rReo dr \    уз 3 r

l^pw) )⁺

+ ^p(2 n +l) Tⁿ (w' + ри) Reo

-

Tⁿ 4 и r Reo l r

-

2,/ i

^- l^pw) ■

puv' + pwv3 + ^pUV = 1- P- (rTⁿ (v' - ^V )) + r    r Reo dr            r J J

+    '+ rT eo у - r),

puw' + pw²p = -3(2n + 1)p +

+ M2 n + 1) Tⁿ Mpw - 2 и '

Reo       l l

-

r Ro ^d (rr ( ^w+pu)) +

2 и )■ l r

uT ' + 23wT                         Tⁿ    2    их 2      _ч2

^p TT-K = ^up+p(2 n + W⁺²R_i|^{u +} ф) ⁺<^pw)J ⁺

⁺ Reo [(" ' ^{- v} ) ^{2 + (w}'^{+ pu ) + (pv)2} ] - IRe, ( ^u'⁺ “ ^+pw ) 2⁺

+ ------—^{1          1} (rTⁿT ')' + 4 3 ²( n + 1) T ⁿ⁺¹ •                         (15)

( 7 - 1)5I^ReoPro r

В полученных формулах штрихом обозначены производные по переменной г. Здесь и далее для удобства записи опущены черточки у безразмерных переменных.

Коэффициент /3 может быть как положительным, так и отрицательным, и отвечает за скорость роста либо затухания газодинамических переменных. Введенный выше параметр L представляет собой расстояние вдоль оси z, на котором скорость и изменится в е раз.

Граничные условия на оси вихря запишем в виде

р(0) = 1, и(0) = 0, v(0) = 0, ш(0) = 1,

Т (0) = 1,   > 0          .

7^

Из уравнения неразрывности (11) следует, что для производной на оси должно выполняется условие и‘(0) = —nUw(0) = —nU.

Для определения граничного условия на азимутальную компоненту скорости обратимся к формуле для завихренности течения:

dw(r, z)

dr J +

1 drv(r, z)

^z г dr ,

П = rot V = , 777+ e, (9U<7 dz          dz или через автомодельные переменные:

П = e.Uve^ + e, (Uu —    e?z + ez-^e^ = dr J        г dr

-— e - Uv + e ,

Uu- — 7) + e z¹ TV у dr J r dr J

Здесь e_r, eg, e _z единичные направляющие векторы в цилиндрической системе координат. Откуда видно, что завихренность также автомодельна по переменной z:

П = n (r)e^Pz.

Компонента вектора завихренности вдоль оси z имеет вид

^{1 drv}

Qz = n (r) • e z = --j—. r dr

Раскладывая далее азимутальную компоненту скорости по формуле Тейлора, находим значение завихренности на оси, r = 0:

Qz юДТО^,^.

Откуда v‘(0) = Qz(0)/2 = Qq/2, где Qq — завихрениесть вдоль оси z в центре вихря. Из условия симметрии имеем ш‘(0) = Т ‘(0) = Д(0) = 0.

Будем искать решения, в которых азимутальная компонента скорости затухает на бесконечности:

v ^ 0 при r ^ ^.

Так как переменные r и z отнесены к L, то коэффициент U принимает значения ±1. Для определенности примем далее U = —1-

3.    Течение в тонком вязком ядре вихря

Пусть г = г 16, где 6 ^ 1. Предположим также, что выполняются условия

∼

7 2

62Reo > 1

Из уравнения неразрывности следует, что нетривиальное решение возможно только при и ~ 6. Введем новую переменную ui = и/6. Тогда в нулевом приближении система автомодельных уравнений (11) - (15) принимает вид

1 d ri dri

(r1pu1) + 2nftpw = 0,

• — = о.

dr1

• ■    R. ^ ^    " (’' — Д)) = 0,

• — (2n + 1)р У-*-    (_Г1Т^п ^ ) =0,

r1Reo dr± у      dr1 у

1 d

(7 - 1)7I^ReoPro n dri

( ПТ" Л =0, drij

решение которой при ft = —1 записывается в конечной форме:

Р = 1, Т = 1,   р =

7^2 ,

ui = nri — ^{n(2n +} 1) Reo6²r3, v = ^° 6ri, 87 2                   2

w = 1

-

⁽²ⁿ TljRa 2 2

⁶ ' , 47 2

или, возвращаясь к переменной r имеем:

и = nr —

п(2п + 1)             По

-----5— Reor , v = —r, 87М 2      0 ’         2 ’

w = 1 —

(2n + 1)Reo 2

------------r

47 2       ’

Откуда легко видеть, что скорость w обращается в ноль на расстоянии r*:

^г * =/

4       2

(2n + 1)Reo ’

а скорость и - на расстоянии r**:

r /    8^ ¹²    =V~2r

^r**   V(2n + 1)Reo       *’

Вычислим теперь компоненту Пг завихренности поля течения:

П = - ^ = П.

r dr

Таким образом, заключаем, что в нулевом приближении в тонком вязком ядре величина завихренности не зависит от r.

4.    Течение вне вязкого ядра

При больших числах Рейнольдса Reo ^ 1 во внешней области вне вязкого ядра в нулевом приближении течение можно считать невязким. Автомодельные уравнения Эйлера тогда принимают вид

1 d - — (гри) + 2nppw = О, r dr (16) рии' + pwuP — Р— = -р', r (17) риг' + pwvP + РиГ = о, r (18) puwf + pw2p = —Р(2п + 1)р, (19) uT ‘ + 2PwT     .

^Р~( ----1.1-’ = ^{up + Р(2п + 1)w}’                        (²⁰)

(7 - 1)Мо

Уравнение энергии записывается в виде r (rp“ ((7-1М + т)) + 2("+1)ppw ((ДДДо + \) = 0’ где Р2 = u2 + г2 + w2. Интегрирование полученного выражения с учетом уравнения неразрывности дает ту2

]Д7—М2_ 27. = | Р^иг ( Ра    , Т 2 А     \U2U2r2

b-lM + 2

где величины с индексом 2 относятся к внешней границе вязкого ядра. Второе уравнение импульсов можно также проинтегрировать:

rv / pur 7 ^2п Г2 V2       Р2и2Г2 ’

откуда находим выражение для температуры:

^T = /    ^T2    + ^и2±^ш2 + Г2 Л - / Т_2 \²77 / Р^иг

(7 - 1)712    7(7 - 1)712       2        2          r         Р2и2г2

Из системы уравнений (16) - (20), с учетом интегралов (21) и (22), при радиальной скорости и » 1 можно получить простое решение. Уравнение неразрывности в этом случае принимает вид

)

-

и² + ш² 2

-   (гри) ^ 0’ r ar откуда следует, что rpu = const. Тогда для азимутальной скорости имеем r2V2 v ^----.

r

Из полученной формулы также видно, что проекция завихренности на ось z во внешней области мала:

^

¹^ «о r dr

Уравнения импульсов (17), (19) упрощаются:

puu' « 0, puw' « 0, откуда u ~ con st, w ~ const. Тогда для плотности и температуры газа во внешней области (вне вязкого ядра) окончательно получаем

_ p2r2       _ . (7 - 1^2 2 б^Ур p ~ —  T ^ T2 + —2~M0v2 /1 - (7) )• т.е. азимутальная скорость v и плотность p при r ^ от убывают практически до нулевых значений.

5.    Численное решение системы автомодельных уравнений

В произвольном случае нелинейная система обыкновенных дифференциальных уравнений (11) - (15) для аналитического исследования представляется архисложной, поэтому воспользуемся численными методами. Систему будем решать относительно функций u(r), v(r), w(r), Т (r) и p(r). Задача сводится к краевой, с начальными условиями в точке r — 0. В расчетах использована неявная схема второго порядка точности, шаг интегрирования: Ar — 10^-5.

В ходе численного решения оказалось, что на некотором расстоянии r от оси радиальная скорость u, плотность p и температура Т претерпевают разрыв. Образуется косой скачек уплотнения, фронт которого расположен на поверхности цилиндра (рис. 1). Стоит, однако, отметить, что при более грубом шаге интегрирования Ar > 10^-4 разрыв может не наблюдаться. В этом случае численное интегрирование заканчивается в точке, где радиальная скорость u и температура Т обращаются в ноль, а плотность р, азимутальная v и продольная w компоненты вектора скорости V стремятся к бесконечности. Подобное поведение решения, связанное с большим шагом интегрирования, является либо артефактом, либо оно указывает на возможность непрерывного решения. Окончательно выяснить этот вопрос авторам не удалось.

В настоящей работе представлено разрывное решение. Для этого в расчетах с малым шагом интегрирования использована комбинированная расчетная схема, когда в вязком ядре вблизи оси (0 < r < r) решаются уравнения Навье - Стокса, а во внешней области (r > г) — уравнения Эйлера.

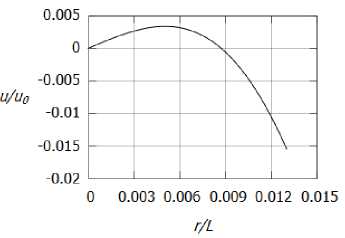
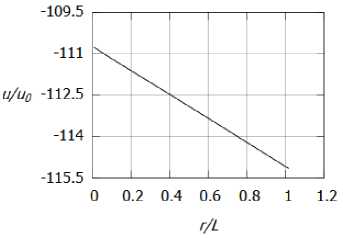
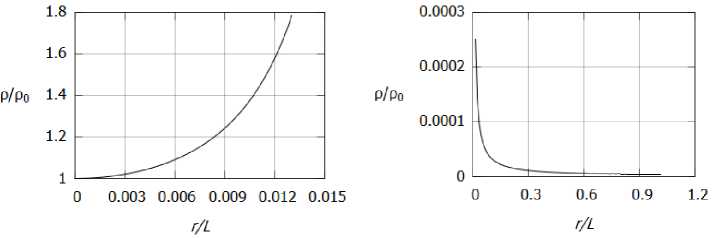
На рисунках 2а, 26 изображены профили радиальной скорости u соответственно во внутренней и внешней областях при Mg — 0.5, Reg — 10000, п — 1, 7 — 1.4. На рисунках За, 36 изображены соответствующие эпюры плотности (течение направлено из бесконечности в сторону оси вихря).

Как видно из рисунков 2, 3, перепад скорости и плотности перед и после ударной волны оказывается выше предельного теоретического значения, соответствующего течению совершенного газа без подвода/отвода тепла. Физически подобная картина течения возможна, например, если на ударной волне имеет место отвод энергии, например из-за протекающих эндотермических химических реакций.

Закон сохранения потоков массы, импульса и энергии в автомодельных переменных имеет вид poutuout — Pinyin,

2   , poutTout poutuout +     , ,2

7^ Ig

^p in ^u in +

P in y in

7^ 10 ’

^T out , ^u out , _{n —} (^{7 —} Ф Ig ²

Т-

± in

(7 - Ф10

, ^u2 n + 2 .

а)                                            б)

Рис. 2. Распределение радиальной скорости и: а) в вязком ядре, б) во внешней области

а)

б)

Рис. 3. Распределение плотности р: а) в вязком ядре, б) во внешней области

Здесь параметры p_out, u_out, T_out отнесены к внешней невязкой области, a p t _n, U i _n, Т { _п — к области вязкого ядра, находящейся за скачком уплотнения; q — теплота, которая поглощается при прохождении ударной волны, q <  0. В расчетах положение ударной волны оказалось на расстоянии г « 0.013 пр и q = -6132, p_in = 1.7856, u_in = -0.0154, T_in = 0.5973 и P out = 0.00025, u_out = -110.8, T_out = 0.293. Заметим, что в произведенных расчетах значение г оказал ось больше г**.

а)

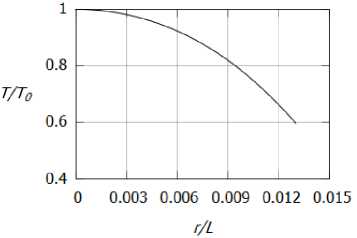
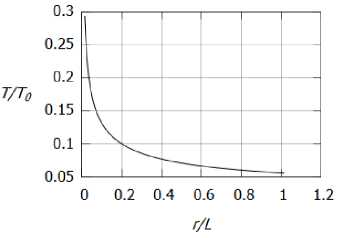
Рис. 4. Зависимость температуры от расстояния: а) в вязком ядре, б) во внешней области

б)

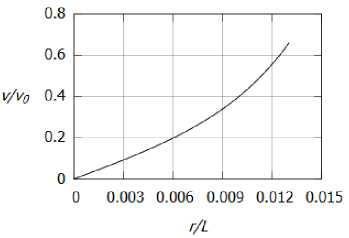
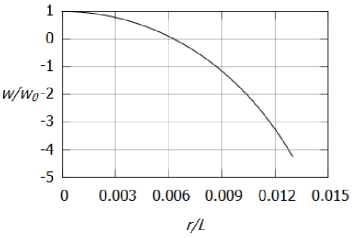
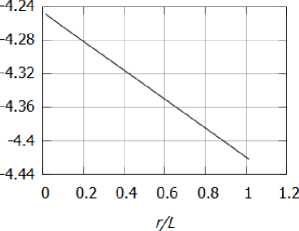
На рисунках 4а и 46, 5а и 56, ба и 66 изображены профили температуры Т, азимутальной скорости v и осевой скорости w соответственно. Из рисунков 4, 5 видно, что температура и азимутальная компонента скорости убывают при г ^ от.

Представляет интерес физическая картина течения в вязком ядре. Формула для линий тока имеет вид dr rdO dz и(г, z)     v(r, z)    w(r, z), или в автомодельных переменных:

dr rdd       dz

u(r)e d ^z    v(r)e d ^z    w(r)e d ^z

Отсюда можно выразить азимутальную и продольную координаты как функции от r:

v(r)dr ru(r) ’

/ w(r)dr u(r) ■

На рисунке 7 изображена полученная зависимость z = z(r). На некотором расстоянии r* от оси поток разворачивается и течет вниз от оси вихря. На расстоянии r = r** радиальная компонента скорости u обращается в ноль, и течение направлено строго вниз, а при r > r** поток течет из бесконечности в сторону оси z.

а)

Рис. 5. Зависимость азимутальной скорости от расстояния: а) в вязком ядре, б) во внешней области

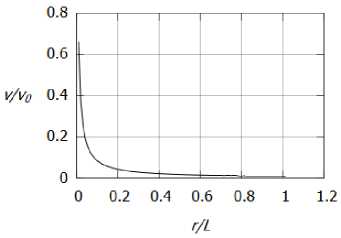
б)

а)

Рис. 6. Зависимость продольной скорости от расстояния: а)

w/w0

б)

в вязком ядре, б) во внешней области

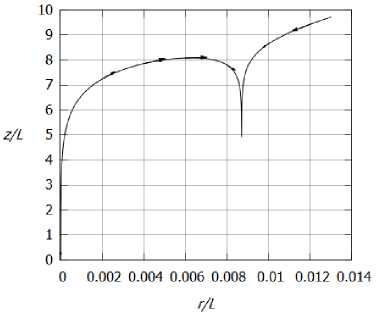
Рис. 7. Линии тока в вязком ядре в плоскости rz

На рисунке 8 дано качественное изображение винтовой линии в трехмернвж координатах (приведен всего один виток). На расстоянии г = г** поток движется по окружности строго вниз, а линия тока в этом месте имеет излом. Для более наглядного представления вихря на рис. 9 изображена винтовая линия с большим числом витков.

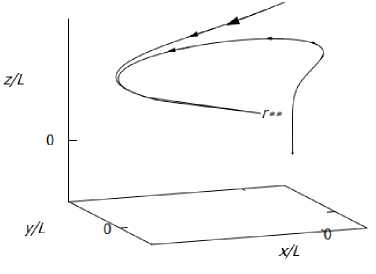
Рис. 8. Винтовая линия тока в вязком ядре

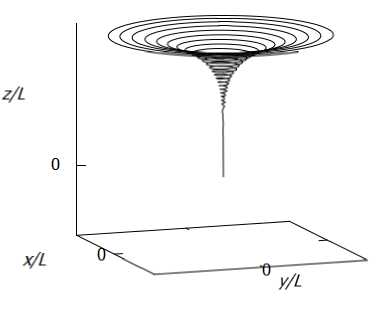
Рис. 9. Винтовая линия тока для восходящего потока

В центре вихря наблюдается сильное восходящее течение с дальнейшей закруткой потока вверх по течению. На внешней границе области поток напротив обладает нисходящим движением, что напоминает картину течения в торнадо.

6.    Заключение