Точное решение уравнений пластичности плоского напряженного состояния

Рассмотрим уравнения, описывающие плоское напря-

и = tu ( у ), v = tv ( у ).

женное состояние в случае медленных нестационарных

течений. Уравнения имеют вид

д и дст, дт _ д v — + —- + — = 0, —	дт дст + — + —- = 0,	(1)
д t   д x   д у      д t	д x   д у
ст 2 + ст 2 - ст ст + xyxy	3 т 2 = 3 к 2,	(2)

д и        д v     дv + ди дx   =   дУ    = дx дУ = X-1        (3)

2^x    у    2Су стx       6т          ’ где стx, стy, т - компоненты тензора напряжений; к - по-

Подставим (6) в (5), в результате получим систему обыкновенных дифференциальных уравнений для определения u , v :

, d ки'       — к      kv‘       п и + -—,         = о, v +--,         = 0. (7)

^ку V4 v ^,2 + и ^{,2           ку} 4 v ^,2 + и^,2

Здесь штрих означает производную по переменной y .

Пусть 2 v' = w sin 9, 2 и ' = w cos 9, тогда система (7) запишется в виде

стоянная пластичности; u , v – компоненты вектора скорости; l – некоторая положительная функция, определяемая по условию пластичности (2). Уравнения (1) – это условия равновесия, (3) – закон течения. Из (1)…(3) полу-

и + k — cos 9 = 0, v + 2 к — sin 9 = 0. dydy

чаем

^Г д и д v 1 J д v д и 1 3 ст_г = XI 2--+— 1 , 3 ст„ = XI 2--+— I ,

( д x д у )         ( д у д x )

,    . Г д v д и 1

6 т = XI +— I .

(д x д у J

С учетом (4) уравнения (1)…(3) запишутся в виде

. XГ_д и д v ) _ X Г дv ди ) д I 2 + I д I+ I ди + 3 ( дx ду ) + 6 ( дx ду ) 0

д t          д x                д у           '

- X Г д v  д и ) - X Г д и   t; v )

д I+ I д I+ 2I д v    6 ( дx  ду J 3 ( дx   ду J о д t         дx                ду           '

3V3 к X^{- 1}

Г , д и д v 1   Г д и , д v 1

I 2 — + — I +I — + 2— I -

( д x д у J   (д x    д у J

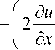
д v V ди , д v 1 + — II — + 2— I ду J(дx    ду J

3 Г д v д и + ^_I ~ ⁺ ~

4 ( д x д у

Продифференцируем (8) по y и c учетом введенных выше обозначений получим d2d wcos9 + к —^cos9 = 0, wsin9 + 4k—^sin9 = 0. (9) dy2

Умножим первое уравнение (9) на - sin 9 , а второе -на cos 9 и сложим:

9"(4cos2 9 + sin2 9)- 39’2 sin 9cos 9 = 0.(10)

Пусть 9' = p (9), тогда 9" = p‘p и уравнение (10) запишется в виде p'(4cos2 9 + sin2 9)-3psin9cos9 = 0.

Интегрируя его, получим p=9= I c 2 , \ 1 + 3cos2 9

где с – произвольная постоянная. Следовательно, су = j V1 + 3cos2 9к9 =

J OtI²   .       1 Г ./ri

1 - — sin² 9 к 9 = ¹ E 9 ,— ,   (11)

MJ 4 I 2 J

Можно показать, что уравнения (5) допускают оператор д    д    д

X = t—+ и+ v— д t    ди    д v в смысле Ли. Поэтому решение уравнений (5) можно искать в виде и = tu(x, у), v = tv(x, у).

Решения такого вида могут быть использованы для описания движений с постоянным ускорением. В данной статье мы ограничимся решениями вида

„L V31               „ где EI 9, -2- I - эллиптический интеграл второго рода.

Из формулы (11) следует, что 9 = 9 ( у ) - монотонно возрастающая функция при c >  0. Поскольк у

9      / c 2 ,

V1 + 3cos² 9

то из формул (8) получаем

, d           ck sin 9

и = - к — cos 9 = ,      =,

^—у       V1 + 3cos² 9

Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева ck cos 0

V1 + 3cos² 0

d v = -2 k — sin 0 = -dy

Компоненты тензора напряжений в этом случае бу- дут т = k cos 0,

CT _y = 2 k sin 0 , a x = k sin 0 .              (13)

Дадим одну из возможных интерпретаций построен- ного решения (11)…(13). Пусть

i n Vs । y, = E4,уJ, y2 = E^

3п Уз

4,2

тогда

т(у, ) = k "22, ct y(y,) = У2k,

u ( У , ) = ck-5-, v ⁽ y , ) = ^- ck -55,

^{т (} У 2 ) = ^{- k} -^2,

CT _y ( y 2 ) = - 72 k , u ⁽ y 2 ) = ^- ck -y-, ^{v (} У 2 ) = ^ck y^-. ⁽¹⁴⁾

Это означает, что верхняя шероховатая жесткая плита, заданная уравнением y = y ₁, движется вниз и вправо с постоянными ускорениями. На плите задано постоянное нормальное и касательные напряжения. Вторая плита (ее уравнение y = y ₂), движется вверх и влево с постоянными ускорениями. На этой плите также заданы нормальное и касательное напряжения.

Замечание. Подобные решения можно построить и для описания сжатия трубы, стенки которой движутся с постоянным ускорением.

S. I. Senashov, V. I. Burmak

EXACT SOLUTIONS OF EQUATIONOF PLASTICITY OF PLANE STRESS CONDITION

The article presents a new exact solution of equation of plane stress state, which describes compression of plastic layer with rigid sheet, which come close to constant acceleration.