Точное решение задачи об акустике в произвольной многослойной среде при контактном взаимодействии с клиновидным штампом

PNRPU MECHANICS BULLETIN

Анизотропия свойственна многим материалам, применяемым в инженерной практике [1], электронике [2], кристаллофизике [3], науках о Земле [4; 5] и во многих других областях. Анизотропия всегда возникает в задачах при рассмотрении движущегося объекта в упругой среде [6; 7]. Смешанные задачи математической физики, к числу которых относится ряд задач о распространении радиоволн [8; 9], контактные задачи [10; 11], задачи акустики [12; 13], теории прочности [14] и других областей, часто приводятся к решению интегральных уравнений Винера - Хопфа [15]. Этим методом удается точно решать только одномерные смешанные задачи, или некоторые пространственные, сводящиеся к одномерным. Двумерные смешанные задачи решаются приближенно, асимптотическими [16] или численными методами [17], в частности, используя для их развития точные решения одномерных интегральных уравнений Винера - Хопфа. В случае анизотропных сред эти методы неэффективны [10]. Прогресс в этой области может дать построение точного решения двумерного интегрального уравнения Винера - Хопфа в анизотропном случае. В работе [18] универсальным методом моделирования для случая изотропной среды впервые было построено точное решение двумерного интегрального уравнения Винера - Хопфа в первом квадранте. В настоящей работе другим подходом, развитым в [19], впервые построено точное решение интегрального уравнения Винера - Хопфа в анизотропном случае. Как частный случай, анизотропные материалы включают композитные материалы и кристаллы, монокристаллы с изменяющимися свойствами при горизонтальном повороте осей координат. Также к ним относятся волокнистые и пленочные материалы, армированные пластики, пьезокварц, графит и другие природные и искусственно созданные материалы с горизонтально изменяющимися свойствами.

1. Постановка задачи

Рассматривается интегральное уравнение Винера -Хопфа, заданное в первом квадранте [18]. Оно имеет вид

∞∞

Кq = J J k(x - ^, y - n)qfe n)d§dn = f (x, y),

0 0

0 < x < «, 0 < y < «;

^{k (} x , у ) = ТГ f I K ^{( a},^{в )} e - ^V,

¹ d a d в ,         (1)

∞∞

Q ( a , в ) = JJ q & П ) ■      ddd П ,

0 0

∞∞ f (x, y) = — J Jf(X, ц)e"* 4п2 Ц

- i ( X x + ц y )

d X d ц .

Функция K ( а, в ), в общем случае комплекснозначная, порождается решением анизотропной граничной задачи в многослойной среде, является непрерывной и суммируемой на осях по обоим аргументам, с поведением на бесконечности вида

K ( а , в ) = O ( а^{- 1} ), в = const; (2) K ( а , в ) = O ( в^{- 1} ), а = const, |а| , |P|^l .

Для интегрального уравнения (1) справедливы теоремы единственности [10].

Теорема 1. Пусть вещественная или мнимая составляющие функции K ( а , в ) знакопостоянные на вещественных осях а , в . Тогда интегральное уравнение (1) имеет единственное решение.

Для случая динамических контактных задач справедлива приведенная ниже теорема единственности [10].

Теорема 2. Пусть вещественные полюсы мероморфной функции K ( а , в ) последовательно чередуются с нулями при движении по контурам Г , , Г ₂ . Тогда интегральное уравнение (1) имеет единственное решение.

Анализ решения двумерного интегрального уравнений Винера - Хопфа, построенного для случая изотропной среды в [18], показал, что для перехода к решению двумерного интегрального уравнения (1) в анизотропном случае необходимы некоторые преобразования в представлении правой части f ( x , y ) рассматриваемого уравнений.

Представим правую часть f ( x , y ) в форме

∞∞ f (x, y) = — f J F(X, p)e-4n2 -L -L

- i ( X x +p y )

d X d p .

В силу линейности интегрального уравнения достаточно рассмотреть правую часть в форме F ( X , p ) e - ^{1 ( X x ;p} y ) . Решив интегральное уравнение с этой правой частью, после этого интегрированием по параметрам X , p получим решение с правой частью (3). Не нарушая общности, возьмем представление подынтегральной функции в виде, которое осуществимо разными способами.

F ( X , p ) e ^{- 1 ( X x +p} y ) = f ( x , X , p ) + f , ( y , X , p ) = f ( x , y , X , p ).

Как показано в [18], это позволит построить решение двумерного интегрального уравнения Винера -Хопфа избранным подходом.

Для решения применим подход, использованный в работе [19].

Для этого заданное в первом квадранте О,, уравнение (2) продолжим новыми неизвестными Ф ₁₂( x , у ), ф ₂₁( x , y ), ф ₂₂( x , y ), с носителями Q ₁₂, Q ₂₁, Q ₂₂ соответственно на всю плоскость. Тогда получим интегральное уравнение (2) в виде

J J K ( а,в ) Q ( а , в ) e ^{- 1( o} x ^+в y ) d а d в =

^{4 п} Г ₁ Г 2

= J J f ( x , y , X , p ) d X d p + Ф 12 ( x , y ) +

Г1 Г

+ Ф 21⁽ x , у ) + Ф 22⁽ x , у )                   ⁽⁴⁾

После применения преобразования Фурье продолженное интегральное уравнение (4) принимает вид

K ( а , в ) Q ( а , в ) -Ф 12 ( а , в ) -Ф 21 ( а , в ) -

- Ф 22 ( а , в ) - F ( а , в , X , p ) = 0.

Здесь F ( а , в , X , p ) = { F ( а , в ) } а + { F ( а , в ) } +.

В дальнейшем ради краткости параметры X , p в (4) опустим и вернемся к ним лишь при описании решения с правой частью f ( x , y ).

В результате выполненных построений, аналогичных использованным в [18], получено точное решение интегрального уравнения (1) в виде

∞∞

q ( x , у )    , f f q ( x , у , X , p ) e - ^{1 ( X x} " y ) d X d p ,

4n2 -L -L

q ( x , y , X , p ) = -^f J Q ( а , в , X , p ) e ' ^{+в y} ) d а d в , 4 п ² Г ₁ Г₂

Q ( а , в , X , p ) = Q 1 ( а , в , X , p ) + Q 2 ( а , в , X , p ).

Здесь приняты обозначения

Q 1 ( а , P , X , p ) = - K - ^|( а , P ) { K __д ( а , в ) { K :P ( а , P ) { F ( а , в ) } ; } - }>

+ K ;> , P ) { Г -К а , в ) ] F ( а , P ) } : } ^;                                (6)

αα

Q 2 < u , в , X , p ) =- K ^{- 1}( а , в ) ] K -а ( а , в ) { K :а ( а , P ) { F ( а , в ) } 2 } а } + +

; K ;P ( а , в ) ] K -К а , в ) { F ( а , в ) } ; } ; .

Операторы в фигурных скобках в (6) детально описаны в [19] и имеют вид

{ G ( а , в ) } + =     J G ^^,^) d ^ , аеП⁺ а,

а 2п 1 Г1 ^ - а

{G(а, в)}-- = -J G^^,^)d^, а € П-.

а    2пi Г ^ - а

{G(а,в)};= -1- JG^^^n)dп, в€п;, в 2п 1 Г П - в

{G(а,в)}-=-JG^^^n)dП, в€П-. в 2п 1 р п-в в

¹ 2

K+а (а, в) = exp-Ljln K ^ в) d ^, аепа, 2п 1 Г1 ^ - а

K-а (а, в) = exp ( - -Ljln K^ в) d^ ), аеПа, 2п 1 Г ^ - а

Г 1 С ln K ( a , п) . о ^к _+р ( а , ^{р )} = exp — I--- d п , РеЦз , 2 п i г п-в

K - _р ( а , в ) = exp ( - -^J ln K ( О , ^{П )} d П ) , в-И . 2 п i Г п-в

Исследование свойств решения смешанной граничной задачи на поверхности вне штампа осуществляется оценкой поведения соответствующих функций. Для этого используем следующие представления поверхности вне зоны контакта

Здесь П О, П О - комплексные области выше, плюс, и ниже, минус контура Г 1 , а П + , П - - области правее, плюс, и левее, минус контура Г ₂.

В результате подстановки построенного решения в левую часть уравнения (1), взятого в форме

4 п ²

JI

г, Г

K ( а, в ) Q ( а , в ) e - ⁱ⁽ ° x ^{+в y} ) d а d в =

= Ф 12^{( x} , У ) ⁺ Ф 21^{( x} , У ) ⁺ Ф 22^{( x} , У ).

4 п ²

JJ

K ( а, в ) Q ( а , в ) e - ⁱ⁽ ° x ^{+в У} ) d а d в = f ( x , У ),

Г , Г 2

несложно убедиться, использовав свойства операторов (6), (7), в его точном удовлетворении.

2. Исследование акустических свойств поверхности вне зоны контакта

В том случае, когда функция K ( а, в ) является анизотропной мероморфной по обоим комплексным переменным [10], нулевые и полярные множества которой представляют аналитические кривые двух комплексных переменных. Предполагается, что полярные множества разрешимы относительно параметров и представимы в виде а _n =а _n (Р), в _n =в _n ( а ). В динамических смешанных граничных задачах вещественным может быть конечное число полюсов [10]. Контуры Г 1 , Г ₂ лежат на вещественной оси комплексных плоскостей а , в всюду, кроме зон появления на вещественных осях вещественных полюсов функции K ( а , в ). В этом случае в достаточно узких зонах вещественных осей они отклоняются в комплексную плоскость, обходя полюса. Контуры выбираются таким образом, чтобы в случаях гармонических по времени смешанных граничных задач была бы физически оправданная постановка граничных задач – на бесконечности обязан правильно выполняться принцип излучения, состоящий в направленности фазовых скоростей на бесконечность для нормальных материалов и из бесконечности – для мезоматериалов электроники [10]. В первом случае в первом квадранте вещественные полюса символа K ( а , в ) обходятся контурами сверху, если при переходе к комплексным амплитудам принята функция exp( - i to t ), to - частота колебаний, t – время. Во втором случае обход в первом квадранте осуществляется снизу. Во втором квадранте положение контуров противоположное. В то же время решение указанного интегрального уравнения и ему подобных имеет важные применения в фундаментостроении, сейсмологии, в устройствах элементной базы электроники, при изучении смешанных граничных задач о поведении плазмы в разных состояниях и в ряде других важных технических областях.

Дальние зоны носителей функций ф ₁₂( x , у ), Ф ₂₁ ( x , у ), ф ₂₂ ( x , у ) по отношению к источнику характеризуются следующими неравенствами

Фп( x , У ): x <  °, У >  °, | х | <<  1

Ф 2, ( x , У ): x <  °, У <  °, | x | <<  1, |у| <<  1

Ф 22 ( x , у ): x >  °, у <  °, |у| <<  1.

С учетом этих свойств исследуем волновое поле вне штампа. Воспользуемся свойством разложимости мероморфной функции K ( а , в ) по простейшим рациональным с помощью полюсов [10]. Справедливы формулы

K(а, в) = Z ----' '!

„ а-а n + ( в ) „ а-а n - ( в )

С „С „ к (а, в) = У —     + У —'.

„ в-в n + (а) Z в-в n - (а)

В том случае, если материал анизотропной среды не обладает мезосвойствами, имеют место следующие свойств полюсов [10]

Re а n + ( в ) >  °, Im а n ₊ ( в ) >  °, Re а n - ( в ) <  °, Im а n - ( в ) <  °, Re в n + ( а ) >  °, Im в n + ( а ) >  °, Re в n - ( а ) <  °, Im в n - ( а ) <  °.

Полученный интеграл в дальней зоне при x ^ -да можно оценить методом стационарной фазы [20]. В результате получаем представление вида

ф ₁₂( x , У ) =          [ к ( а , в ) Q ( а , в ) e ^{- i(} ° x ^{+в У} ) d а d в ~

4п г Г

~ ^2 J JZ

-г^п_Г] _г2 n

C n ^а+ Q ^{( а} , ^{в )} e - ⁱ⁽ _a x ^{+в y} ) q ( а , в ) d а d в = ^а-а n + ^{( в )}

= Z C n а+ Q ( а n + ( в ), в ) e ^{- 1 ( а} n ^{+ ( в )} x ^{+в У} ) d в . 2 л / ₂   n

В результате преобразований находим

Ф 12 ^{( x} , У ) = Z n

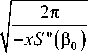
f ( Р а )

exp ^{- ix}S ( р ° ) ⁺ i n sgn S "( 3 ° ) |j ⁺ O ⁽ x ^{- 1)} ] ,

x <  °, | x | >>  1 (8)

f ( Р ) = ^ C n а+ Q [ а n + ( в ), Р ] , S ( в ) = а n + ( в ) -в k 1 , 2 п

S ' ( P ° ) = °, S '' ( p ° ) * °, y = - k 1 x , k 1 >  °

Аналогично имеем

Ф 22 ( x , у ) = Af f K ( а , в ) Q ( а , в ) e ^{- i( a x +в} y ) d а d в- ^{4 п} г , г

—C      e ^- i ^w+в y ) Q ( а , в ) d а d в =

в-в n + (а)

~

- 41 2 J JZ

^П Г 1 г ₂ n

= J 7 C n в+ Q( а , в n + ( a )) e ^{- i W+в} n ^{+ ( а ) у} ) d а . ^Г n

Ф ( х , у ) = У ---2П—- f (а₀)

22        7 --у5"(а0) ( 0)

exp -iy5(а0) + 4sgn5"(а0) [1 + O(у-1)], f (а) = / Cnв+ Q[ а, вn + (а) ], 5 («) = -«k2 +вn + (а), 2п

5 ' ( а₀ ) = 0, 5 "( в₀ ) * 0, х = - k ₂ у , к ₂ > 0.

Несложный анализ позволяет получить асимптотическое поведение поверхности ф ₂₁( х , у ). Для у = кх главный член асимптотики в дальней зоне на выбранных прямых получается описанным ранее способом и имеет вид

2 п

Ф,|(ху)- 77 -х^чмf (в0)х хexp -ix5(в0) + insgn5''(ва) [1 + O(х 1)] +

■f ( а ₀ ) exp - iy5 ( а ₀ ) + у sgn 5 '' ( а 0 ) х ⁽¹⁰⁾

^-»        2п

⁺⁷    - у5 '' ( а 0 )

х[ 1 + O ( у ^{- 1}) ] ,

5 ( в ) = а n + ( в ) + в к , 5 ( а ) = а к ^{- 1} + в n + ( а ).

Среди а _{n +} ( в ₀), в _{n +} ( а ₀) следует выбрать имеющие минимальную мнимую составляющие, они будут представлять главные члены асимптотики в дальней зоне. В частности, возникающие при достаточно высокой частоте вещественные нули [10] описывают акустические свойства поверхности многослойной анизотропной среды вне области контакта.

Пример

В качестве примера рассмотрим наиболее сложный случай вычисления комплексных нулей этой функции, взяв для этого мероморфную функцию F ( u ) = K ( и ) +

+ s и , s >  0, встречающуюся в контактных задачах.

4(1 - v ) sh ² и           2 у

K ( и ) =--------------, и =л/а,+а₂ .

и ( sh 2 и + 2 и )            ^{1 2}

На представленных рис. 1, 2 приводятся примеры вычисления параметра а 1 = а 1 ( а ₂) с учетом зависимости от а ₂ для разных комплексных нулей функции

F ( и ). Аналогичный вид имеет зависимость а ₂ = а ₂( а 1 ). Наличие этих соотношений дает возможность для проведения вычислений по формулам (8)–(10).

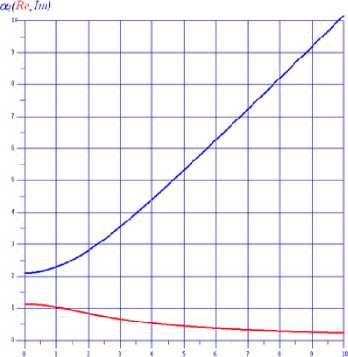
Рис. 1. Верхняя кривая описывает поведение мнимой составляющей функции а 1 =а 1 ( а ₂), а нижняя - вещественной составляющей для параметров v = 0,1; s = 0,1;

и 1 = 1,28153 + 2,027 i

• Fig. 1.    The upper curve describes the behavior of the imaginary component of the function а 1 = а 1 ( а ₂), and the lower one is real component for parameters v = 0,1; s = 0,1; и 1 = 1,28153 + 2,027 i

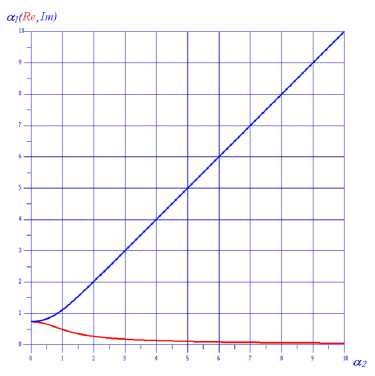
Рис. 2. Верхняя кривая описывает поведение мнимой составляющей функции а 1 = а 1 ( а ₂), а нижний - вещественной составляющей для параметров v = 0,2; s = 1;

u₂ = 0.7417 + 0.743771

• Fig. 2.    The upper curve describes the behavior of the imaginary component of the function а 1 = а 1 ( а ₂), а нижняя - вещественной составляющей для параметров v = 0,2; s = 1;

u₂ = 0.7417 + 0.743771

Заключение

Таким образом, впервые получено точное решение двумерного интегрального уравнения Винера – Хопфа, возникающего в контактной задаче для клиновидного штампа в произвольной анизотропной многослойной среде. Оно позволило изучить акустические свойства анизотропных материалов в дальней зоне вне области контакта. Полученный результат может быть применен к решению значительного числа смешанных задач, иг-