Точностные и вероятностные характеристики алгоритма распознавания режима полета вертолета в радиолокационной системе воздушного базирования

Современные и перспективные вертолеты являются опасными низкоскоростными, маловысотными и высокоманевренными воздушными целями, успешно противостоящими наземным средствам ПВО. Одним из вариантов активного противодействия воздушной цели класса «вертолет» может быть обнаружение его и последующее поражение с борта перспективного авиационного комплекса с помощью управляемой ракеты класса «воздух – воздух» с активной радиолокационной головкой самонаведения.

Для наведения на вертолет необходимо применять метод самонаведения ракеты, соответствующий режиму его полета. Так, метод пропорционального наведения применим при стационарном режиме полета вертолета, метод пропорционального наведения с положительным или отрицательным смещением – при полете вертолета с ускорением или торможением, метод погони с дополнительным углом упреждения – при полете вертолета в режиме «висение».

Очевидно, что выбор того или иного метода самонаведения должен осуществляться на основе распознавания режима полета вертолета в радиолокационной системе воздушного базирования. При этом установлено, что информативным параметром отраженного от вертолета радиолокационного сигнала является изменение во времени его доплеровской частоты, обусловленной скоростью сближения ракеты с вертолетом. В настоящее время режим такого распознавания режима полета вертолета в радиолокационной системе воздушного базирования в интересах последующего выбора, соответствующего метода самонаведения ракеты отсутствует.

Цель работы – разработка алгоритма распознавания режима полета вертолета в радиолокационной системе воздушного базирования, который обеспечивал бы выбор соответствующего метода самонаведения ракеты на него и получение точностных и вероятностных характеристик.

Разработку алгоритма распознавания произведем при частично заданной структуре автоселектора скорости радиолокационной системы воздушного базирования (РЛС ВБ) и наличии измерений дальности и собственного ускорения носителя. Пусть справедлива гипотеза Г_ij о том, что в каждый дискретный момент времени на выходе блока дискретной логики формируются отсчеты доплеровской частоты, обусловленной скоростью сближения носителя РЛС ВБ с вертолетом, соответствующие i -му режиму и j -му набору параметров полета вертолета. При этом справедливы условия (1) и (2).

Р ( r j ) = P ij , i = 1,4, j = 1, 7, (1)

4 J

ZZ P j = 1, (2) i = 1 j = 1

где P_ij – вероятность того, что на выходе блока дискретной логики имеется отсчет доплеровской частоты, соответствующий i -му режиму полета вертолета с j -м набором его параметров.

В общем случае наблюдение на входе синтезируемого алгоритма на k -м шаге его работы для каждой гипотезы Г ij будет иметь следующий вид:

Г ij : Y ij ( k ) = H ij ( k ) X ij ( k ) + ξ ij ( k ), (3)

где X _ij – вектор состояния, фазовыми компонентами которого являются оцененные значения доплеровской частоты, дальности до вертолета и собственного ускорения носителя РЛС ВБ в радиальном направлении; H _ij – переходная матрица наблюдения; ξ _ij – вектор-столбец шумов наблюдения, представляющий собой гауссовские «белые» последовательности с нулевым математическими ожиданиями (МОЖ) и матрицей спектральных плотностей N ξ .

Исходя из этого оценка доплеровских частот с учетом дальности до вертолета и собственного ускорения носителя РЛС ВБ должна производиться в нескольких оптимальных фильтрах (ОФ), в каждом из которых априорные сведения, принятые при фильтрации, соответствуют определенной гипотезе относительно режима полета вертолета, т. е. блок оценок в алгоритме распознавания должен быть многоканальным по числу i = 1 , 4.

Кроме того, при справедливости гипотезы относительно i -го режима полета вертолета может иметь место J наборов параметров его полета. В результате блок оценок должен быть многоканальным и по числу наборов параметров полета вертолета при каждой принятой гипотезе относительно режима его полета. Отсюда следует, что блок оценок должен представлять собой матрицу оптимальных фильтров, в каждом из которых производится совместная фильтрация последовательных дискретных отсчетов доплеровских частот, дальности и собственного ускорения. На основе наблюдения (3) в каждом ОФ с учетом принятых априорных сведений производится оценивание истинного вектора состояния X ( k ).

Из полученной совокупности оценок необходимо выбрать только одну Х д , которая в соответствии с выбранным критерием оптимальности была бы наиболее близка к истинному вектору X ij , т.е. гипотезе Г ij .

При условии, что модель наблюдения и вектор состояния являются линейными, можно использовать для синтеза каждого оптимального фильтра многомерную линейную калманов- скую фильтрацию, описываемую, как [1, 2, 3]

P - (к +1) = Ф( k )P (к )ФТ (k) + Q( к +1);(4)

¥( к +1) = H( k + 1)P - (k + 1)HT (k +1) + R( k +1);(5)

K(k +1) = P - (k + 1)HT (k +1) T (k +1);(6)

_

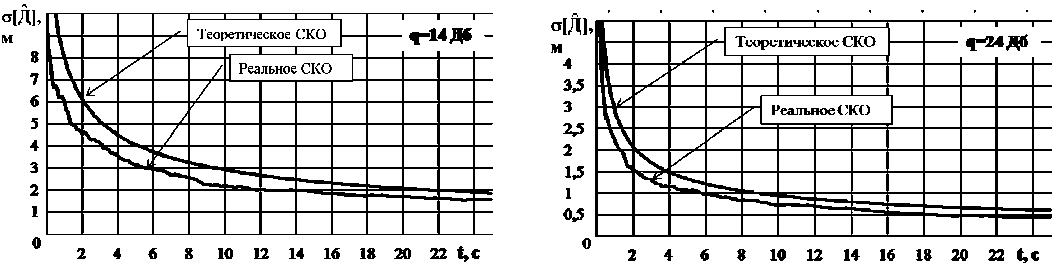
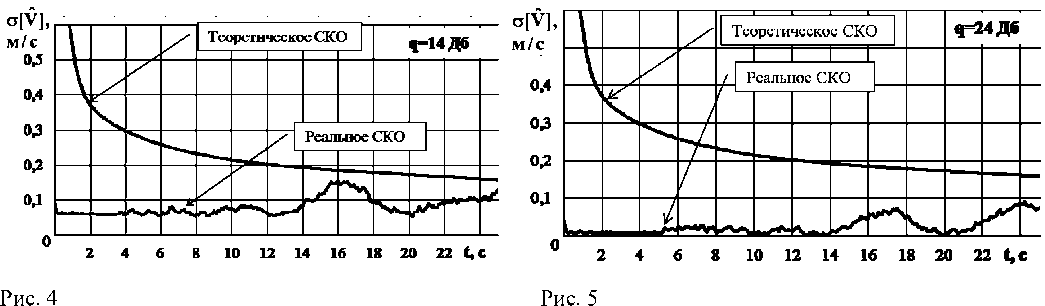
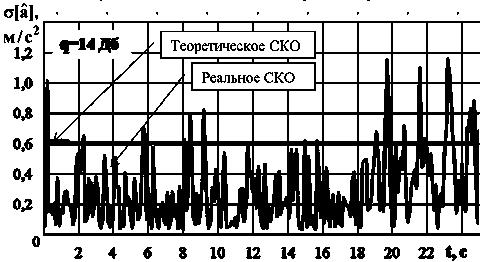
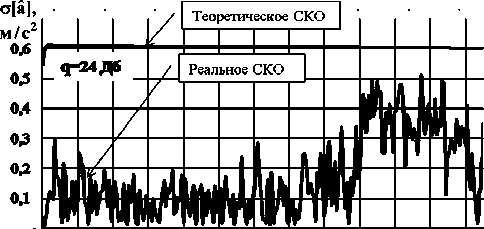
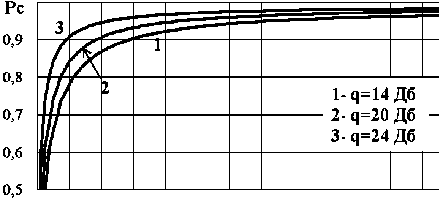
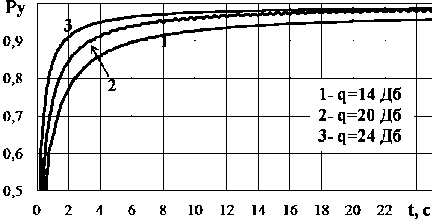
Zk+="'k - -H(k+|)Ф(k ■|)X

X(k+1) Ф(k)x(k)+K(k + i)Z(k+1),(8)

P( k +1) = [I - K (k + 1)H( k + 1)]P - (k +1),(9)

где P (k +1) и P(k +1) - ковариационные матрицы ошибок экстраполяции и фильтрации соответственно, размерности n×n (n – размерность вектора состояния); Ф(k) – переходная матрица состояния размерности n×n; Q(k+1) и R(k+1) – ковариационные матрицы шумов возбуждения и наблюдения размерности n×n и m×m (m – размерность вектора наблюдения) соответственно;

K(k+1) – матрица весовых коэффициентов размерности n×m; Z(k+1) – матрица невязки измерений размерности m×1; I – единичная матрица размерности n×n.

Определим основные матрицы данных уравнений для фильтров, настроенных на стационарный полет вертолета, с ускорением, с торможением и полет в режиме висения.

Стационарный полет вертолета

Система дифференциальных уравнений, описывающих взаимное перемещение носителя РЛС ВБ и вертолета, при его стационарном полете может быть представлена следующим об-

разом: Д (t) = "(ТВ1( t) + A VB1 ( t) + Vh (t) + A Vh (t)),               Д(0) = Д о; • Vb1( t) = 0,                                                    Vbi(0) = Vbio; 0d( t) = 0,                                                    a b1(0) = 0; AVb1( t) = A а в1( t),                                        A Vb1(0) = 0; A аГв1( t) = -«B1A а В1 (t) - Pb1A Vb1( t) + V 2«В1^ а2вв n B1(t),   A a b1 (0) = 0; - VH (t) = 0,                                                    VH (0) = Vh0;   (10) A V. (t) = - ан (t),                                            A Vh (0) = 0; aH (t) = 0,                                                    a н (0) = 0; A ан (t) = -ан A a н (t) - вн A Vн (t) + V 2«н^H n н (t),         A a н (0) = 0; A а (t) = 0,                                                   Aa (0) = A а0; UJa (t) = -aa Ua (t) + ^2 a2 na (t),                      Ua (0) = U a0, где Д – наклонная дальность между носителем РЛС ВБ и вертолетом; Vв1 и ∆Vв1 – детерминированная и флюктуационная составляющие радиальной скорости полета вертолета; aв1 и ∆aв1 – детерминированная и флюктуационная составляющие ускорения вертолета (индекс 1 указывает на стационарный режим полета вертолета); Vн и ∆Vн – детерминированная и флюктуационная составляющие скорости полета носителя РЛС ВБ на участке его самонаведения; aн и ∆aн – детерминированная и флюктуационная составляющие ускорения полета носителя РЛС ВБ на участке его самонаведения; ∆a – постоянная ошибка акселерометра носителя РЛС ВБ, обусловленная погрешностями начальной выставки гироплатформы, нескомпенсированным дрейфом гироскопов; Ua – низкочастотная ошибка измерения, обусловленная шумовыми составляющими ошибок акселерометра [4].

В векторно-матричной форме система уравнений (10) будет иметь следующий вид:

X = AX ₊GN X(0) = X0, (11)

где А – матрица размерности 11х11, имеющая следующие отличные от нуля элементы: a_1,2 = a_1,3 = = a1,6 = a1,7= a6,8= –1; a2,4 = 0; a3,5= a7,9 = a7,10= a7,11 = 1; a5,3 = –βв1; a5,5 = –αв1; a9,7= –βн; a9,9= –αн; a11,11 = –αa; G - матрица размерности 11x11, имеющая следующие ненулевые элементы: g_; = = _лla„iCr2 1 ;

2 |Т , g99 = ^аа^ан ; gп>п = 2аааага ; N = |0,0,0,0,nв1,0,0,0,nн,0,nа - транспонированный вектор формирующих белых гауссовских шумов с нулевыми математическими ожиданиями и единичными интенсивностями, имеющий размерность 11×1.

Элементы переходной матрицы наблюдения Н(k) в уравнении (3) будут определяться, с одной стороны, составом измерителей функционально связанных координат, а с другой – условием наблюдаемости фильтра, которое необходимо обеспечить для предотвращения его расходимости. Исходя из этого переходная матрица наблюдения будет иметь размерность 3×11, а ее ненулевые элементы следующие: h1,1= h2,2= h2,3= h2,6 = h2,7= h3,6 = h3,7= 1.

Элементы вектора шумов наблюдения ξ(k), имеющего размерность 3×1, являются некоррелированными с элементами вектора шумов возбуждения N(k).

Для определения элементов матриц Ф(k) и Q(k) в уравнении (4) необходимо перейти от векторно-матричного дифференциального уравнения (11) в непрерывном времени к аналогичным уравнениям в дискретном виде исходя из следующих соотношений [5]:

Ф(k) = eATg,

Q( k) = M [J( k )J T( k)],(13)

(k+1) Tд

J( k) = J Ф[( k + 1)T - r]G(r)N(r)dr,(14)

kTд где Тд – период дискретизации.

В первом приближении ограничимся линейными членами, т. е.

Ф(k) ≈ I + АTд.(15)

В результате матрица Ф(k) будет иметь следующие отличные от нуля элементы: φ_1,2 = φ_1,3 = = φ_1,6= φ_1,7 = φ_6,8 = –Т_д; φ_3,5 = φ_7,9 = φ_7,10 = φ_7,11 = Т_д; φ_1,1 = φ_2,2 =φ_3,3 = φ_4,4 = φ_6,6 = φ_7,7 = φ_8,8 = φ_10,10 = = 1; φ_5,3 = –β_в1Т_д; φ_5,5 = 1–α_в1Т_д; φ_9,7 = –β_нТ_д; φ_9,9 = 1–α_нТ_д; φ_11,11 = 1–α_aТ_д.

После преобразований, определяемых формулами (13) и (14), и ограничении линейными членами, ненулевыми элементами ковариационной матрицы Q(k) шумов возбуждения будут являться следующие:

q5,5 = ^2а^^ставт;q9,9 = ²«н^H^тд; qii,ii = ²«а^ста^2тд; q9,11 = qii,9 = V^^H^I^O^ITg;

q5,9 = q9,5 = V4«в1СТав1«нСТ2Тд; q5,11 = q_n^ = ^а^ааО-"2Тд.

Полет вертолета с ускорением

Модель вектора состояния, описывающего взаимное перемещение носителя РЛС ВБ и вертолета при его полете с ускорением (индекс 2), представляет собой следующую систему дифференциальных уравнений:

Д (t) = -(Vb2( t) + A Vb2( t) + Vн (t) + A V (t)),	Д(0) = Д 0;
V.;- t ) = a B2( t),	* b2(V)* в20;
Cb2( t) = 0,	aв2(0) = 0;
A Vb2( t) = A а в2( t),	A V32(0) = 0;
Aaie2(t) = -ав2Аав2(t) -Pb2AVb2(t) + V2ae2aавв	n в2 (t),   Aa в2(0)= 0;
VTH (t) = 0,	VH (0) = VH0;       (16)
A V>h( t) = - ан (t),	A VH (0) = 0;
01h (t) = 0,	a н (0) = 0;
A С1н (t) = -ан A a н (t) - ^hA Vн (t) + V^aH^2n н (t),	A aH (0) = 0;
A а (t) = 0,	A а (0) = A ад;
Ua (t) = —aa Ua (t) + V2aa^a na (t),	U a(0)= U a0-

Матрица А размерности 11×11 имеет следующие отличные от нуля элементы: a_1,2 = a_1,3 = = a_1,6 = a_1,7 = a_6,8 = –1; a_2,4 = 1; a_3,5 = a_7,9 = a_7,10 = a_7,11 = 1; a_5,3 = –β_в2; a_5,5 = –α_в2; a_9,7 = –β_н; a_9,9 = –α_н; a11,11 = –αa.

Матрица G размерности 11×11 имеет следующие ненулевые элементы:

g5,5 =             ; g=       2 ; g_u,_n =       ^.

N = |0,0,0,0, n b₂,0,0,0, n н ,0, n_а|Т.

Матрица Ф будет иметь следующие отличные от нуля элементы: φ1,2 = φ1,3 = φ1,6 = φ1,7 = = φ6,8= –Тд; φ3,5 = φ7,9 = φ7,10 = φ7,11 = Тд; φ1,1= φ2,2 = φ3,3 = φ4,4= φ6,6 = φ7,7 = φ8,8 = φ10,10 = 1; φ5,3 = –βв2Тд; φ_5,5 = 1–α_в2Т_д; φ_9,7 = –β_нТ_д; φ_9,9 = 1–α_нТ_д; φ_11,11 = 1–α_aТ_д.

Ненулевыми элементами ковариационной матрицы Q шумов возбуждения будут являться следующие:

2,                    2,                    2                                 2      _2^

q9,9 ²«н^н^Тд; qll,ll ²«а^_а^Тд, q5,5 ²«в^ав^2Тд; q5,9 q9,5 ^“в²^^ав2“н^СТнТд;

/       5       5                       Гл 2     2ГГ~ q5,11 = 911,5 = 4аС2в1ав2в2«аа2Tg; q9,11 - q11,9 - х^^.нн«а^аТд.

Полет вертолета с торможением

Вектор состояния, описывающий взаимное перемещение носителя РЛС ВБ и вертолета при его полете с торможением (индекс 3), имеет следующий вид:

Д (t) = -(Ve3( t) + A Vb3( t) + Vh (t) + A Vh (t)),               Д(0) = До;

^Vb3⁽t) = ^—a b3⁽tX                                          ^Vb3⁽⁰⁾ = ^Vb30^;

ae3⁽t) = 0                                                a B3⁽⁰⁾= 0;

•

^AVb3(t) = ^Aа^в3(t),                        ^AV^B3(0)=^0;

^Aав3⁽t) = ^aB3^Aав3⁽t)^-^b3^AVb3⁽t) + д/2^ав3стОВв Яв3(t) ^Aaв3⁽⁰⁾= ^0;

V_H(t) = °                                            ^vh⁽⁰⁾= ^vh0;⁽¹⁷⁾

^{A V}H ⁽t) = ^—аH ⁽tX                                       ^{A V}H ⁽⁰⁾= ^0;

^ан⁽t) = ⁰                            a^{H (0)}=^0;

^{A а}н ⁽t) = ^—ан ^Aa н ⁽t) ^—Ph^AVн ⁽t) ⁺V ^2анСТнЯн ⁽t),         ^Aa н ⁽⁰⁾= 0;

^{Aa (}t) = 0,                                                   ^{Aa (0)}= ^Aа⁰;

•                                                   2"

^a ⁽t) = ^—«_aUa ⁽t) + V²«_a^а ^Яa ⁽t),                      Ua⁽⁰⁾= UaO-

Матрица А размерности 11×11 имеет следующие отличные от нуля элементы: a_1,2 = a_1,3 = = a1,6 = a1,7 = a6,8 = –1; a2,4 = –1; a3,5 = a7,9 = a7,10 = a7,11 = 1; a5,3 = –βв3; a5,5 = –αв3; a9,7 = –βн; a9,9 = –αн; a11,11 = –αa.

Матрица G размерности 11×11 имеет следующие ненулевые элементы:

2^; ; g,,, = OS; g.,11 = 2^.

Т

^N= |0,0,0,0,nB3,0,0,0,nр ,0,na | .

Матрица Ф будет иметь следующие отличные от нуля элементы: φ1,2 = φ1,3 = φ1,6 = φ1,7 = φ6,8 = = –Тд; φ3,5 = φ7,9 = φ7,10= φ7,11= Тд; φ1,1 = φ2,2 = φ3,3 = φ4,4 = φ6,6 = φ7,7 = φ8,8 = φ10,10 = 1; φ5,3 = –βв3Тд; φ5,5 = = 1–α в3Тд; φ9,7= –βнТд; φ9,9= 1–αнТд; φ11,11 = 1–αaТд.

Ненулевыми элементами ковариационной матрицы Q будут являться следующие: 222 q⁹⁹ = 2=.,нT,;q_lu, = 2=.,аT.^;q5,5 = 2_а13_О„3^Тд;

q5,9 = q9,5 = V4«в3,ав3«н,2T. ; q5Jl = q,, 5 = V4«в3,2в3«а,2T.;

q 9 ,ll = q,l ,9 = ^^н^н²^Hi^a^a T. ■

Полет вертолета в режиме висения

Модель вектора состояния, описывающего взаимное перемещение носителя РЛС ВБ и вертолета при его полете в режиме висения (планерная составляющая спектра сигнала отсутствует, имеет место лишь спектральная составляющая, обусловленная отражениями сигнала от силовой установки вертолета), имеет следующий вид:

VJ (t) = 0,                                   v-! (0) = 0;

aB^y(t) = 0,                                          a_всу (0) = 0;

A V,' (t) = A a By (t),                             A Y^ (0) = 0;

А асу (t) =     A a B^y(t) + 720457 n (t)      A a B^y(0) = 0;

VH (t) = 0,                                       Vн (0) = Vн0;              (18)

A V_h (t) = - а_H (t),                                  A V_h (0) = 0;

ан (t) = 0,                                            a н (0) = 0;

^Aalp⁽t) = ^-«h^Aaн ⁽t) ^-Ph^AVh⁽t) ⁺V²«h^H nн ⁽t), ^Aaн ⁽⁰⁾= 0;

•

^{Aa (}t) = ⁰,              ^{Aa (0)}= ^Aa0;

Ua( t ) = -«a Ua( t ) + V 2«a°'an a( t ),                 Ua(0) = U, где индекс «су» относится к силовой установке вертолета.

Матрица А размерности 11×11 имеет следующие отличные от нуля элементы: a_1,2 = a_1,3 = = a1,6 = a1,7= a6,8= –1; a2,4 = –1; a3,5= a7,9 = a7,10= a7,11 = 1; a5,5 = –αв4; a9,7= –βн; a9,9= –αн; a11,11 = –αa.

Матрица G размерности 11×11 имеет следующие ненулевые элементы:

g 5,5 = V 2«^B-A3; g 9,9=22=^21; g 11,11 = 7 ²«."^a •

N= 0,0,0,0,nв4,0,0,0,nн,0,nа^Т.

Матрица Ф будет иметь следующие отличные от нуля элементы: φ_1,2 = φ_1,3 = φ_1,6 = φ_1,7 = = φ6,8 = –Тд; φ3,5 = φ7,9 = φ7,10 = φ7,11 = Тд; φ1,1 = φ2,2 = φ3,3 = φ4,4 = φ6,6 = φ7,7 = φ8,8 = φ10,10 = 1; φ5,5 = = 1–α_в4Т_д; φ_9,7 = –β_нТ_д; φ_9,9 = 1–α_нТ_д; φ_11,11 = 1–α_aТ_д.

Ненулевыми элементами ковариационной матрицы Q шумов возбуждения будут являться следующие:

q5,5 ⁼²αв4σа²в4^Tд^;q5,9⁼q9,5^{= 4}αв4σа²в4αнσн^2Tд^;

q5,11= q11,5= 4αв4σа²в4αаσа²Tд; q9,9=2αнσн²Tд; q11,11=2αаσа²Tд;

q9,11 ⁼q11,9 ^{= 4}αнσн²αаσа^2Tд^.

После оценки фазовых координат взаимного перемещения вертолета и носителя РЛС ВБ в каждом калмановском фильтре необходимо найти такой ОФ из их матрицы в блоке оценок, в котором априорные сведения относительно режима и набора параметров полета вертолета будут наиболее близки к реально наблюдаемому процессу на его входе. При этом будет иметь место структурная неопределенность, обусловленная множествами гипотез относительно режима полета вертолета, и параметрическая неопределенность, обусловленная множествами гипотез относительно наборов параметров при каждом режиме его полета. Следовательно, в дальнейшем возникает необходимость проверки совокупности гипотез в соответствии с выбранным критерием согласия.

В рамках калмановской теории фильтрации целесообразным является использование критерия согласия χ²-Пирсона, применяемого для проверки соответствия экспериментальных данных теоретической модели [6]. Согласно этому критерию на основе экспериментальных данных (в данном случае наблюдаемого процесса на входе алгоритма распознавания) формируется случайная величина l2, которая при совпадении реального процесса и его модели должна обладать свойствами χ2, т.е. l2 = χ2. Случайная величина l2 при калмановском подходе определяется следующим образом:

l²(k+1)=Z^T(k+1)Ψ^-1(k+1)Z(k+1),                                   (19)

где векторы Ψ(k+1) и Z(k+1) определяются в соответствии с уравнениями (5) и (7) соответственно.

Проверка согласия априорных сведений реально наблюдаемому процессу производится путем вычисления величины l2(к+1) и сравнения ее с граничным значением хгр, соответствую- щим заданным степени свободы Лсв и уровню вероятности ошибки Рош(х > Хгр )• Количество степеней свободы определяется размерностью вектора наблюдения Y(k+1), т.е. Sсв=3. Значения х2 (5св, Рош) табулированы.

Так, если гипотеза Гij верна (при дополнительном условии, что статистические характеристики вектора ξ (k) шумов наблюдения (формула (3)) заданы правильно), то должно выпол-ij няться условие lj(k + 1) < хгрА5св,рош),                                                (20)

в противном случае это условие не выполняется.

Для определенности и упорядочивания примем расположение ОФ в их матрице таким, чтобы в каждой строке матрицы находились бы ОФ с постоянными априорными сведениями о режиме полета вертолета (стационарный полет, с ускорением, с торможением, висения), а в каждом столбце – ОФ с различными априорными сведениями о параметрах полета. Тогда алгоритм нахождения такого ОФ из их матрицы в блоке оценок, в котором априорные сведения относительно режима и набора параметров полета вертолета будут наиболее близки к наблюдаемому процессу на его входе, заключается в следующем.

• 1.    Для каждого оптимального фильтра их матрицы производится вычисление соответствующих значений lj^(k₊1) по формуле ⁽¹⁹⁾.

• 2.    Осуществляется сравнение полученных величин 12 (к +1) с соответствующими значениями хГр _ (5св, Рош) (формула (20)).

• 3.    Определяется максимальный номер строки матрицы оптимальных фильтров, где находится хотя бы один фильтр, для которого выполняется условие (20). Значение номера строки и будет соответствовать оценке режима полета вертолета i .

Условие (20) может быть выполнено сразу в нескольких ОФ данной строки их матрицы, т.е. в общем случае не исключена и параметрическая неопределенность. Разрешение параметрической неопределенности при калмановском подходе возможно произвести по критерию минимума обобщенной дисперсии D_Σ(k+1) действительных ошибок фильтрации в установившемся режиме для всех составляющих вектора X_ˆ (k), определяемую как [1] ij

D, jk₊1) = Z^Т(k + 1)Z;,⁽k +1).                                    (21)

Отсюда следует, что алгоритм определения набора параметров полета вертолета (номера j-го столбца) заключается в том, что для каждого ОФ, определенного выше строки их ма-– 366 – трицы, по формуле (21) производится вычисление соответствующих значений D^ ^. (к +1) и определяется номер столбца матрицы, где находится тот оптимальный фильтр, для которого

-эта величина минимальна. Значению номера столбца и будет соответствовать оценка j -го набора параметров полета вертолета. На рис. 1 представлена структура алгоритма распознавания.

На рис. 1 введены обозначения: 1 – блок оценок; 2 – блок вычисления величины l²; 3 – блок сравнения; УС – устройство сравнения.

Значения точностных и вероятностных характеристик синтезированного алгоритма распознавания были получены путем моделирования. В качестве примера на рис. 2–7 для ситуации стационарного полета вертолета изображены графики временных зависимостей теоретических и реальных среднеквадратических ошибок (СКО) фильтрации дальности «носитель РЛС ВБ – вертолет», скорости полета и ускорения вертолета при значениях отношения сигнал/шум (q) 14 и 24 дБ, которые иллюстрируют качество сходимости работы ОФ. Для других режимов полета вертолета данные оценки также являются сходящимися.

Рис. 1

Fig. 1

Рис. 2                                                 Рис. 3

Fig. 2

Fig. 3

На рис. 8–11 представлены зависимости вероятностей правильного распознавания стационарного режима полета вертолета (РС), с ускорением (РУ), с торможением (РТ), в режиме висения (РВ) при отношениях сигнал/шум 14, 20 и 24 дБ, а в табл. 1 – значения МОЖ (M[·]), СКО (σ[·]) и доверительных интервалов (I_0,95) вероятностей правильного распознавания при времени сопровождения-распознавания 2 с.

Из анализа приведенных результатов следует, что вероятность правильного распознавания режима полета вертолета при времени сопровождения-распознавания 2 с и отношении сиг-нал/шум q = 14…24 дБ составляет:

для стационарного полета – 0,75…0,93;

для полета с ускорением – 0,74…0,91;

Fig. 4

Рис. 6                                                  Рис. 7

Fig. 6                                                         Fig. 7

Fig. 5

2   4   6   8   10 12 14 16 18 20 22 t,c

0   2   4   6   8 10 12 14 16 18 20 22 t, C

Рис. 8

Fig. 8

Рис. 9

Fig. 9

Fig. 10

Fig. 11

Таблица 1

Table 1

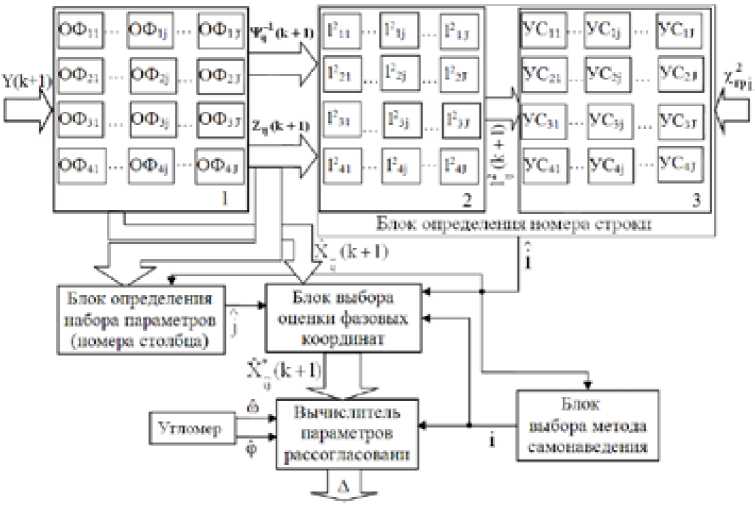
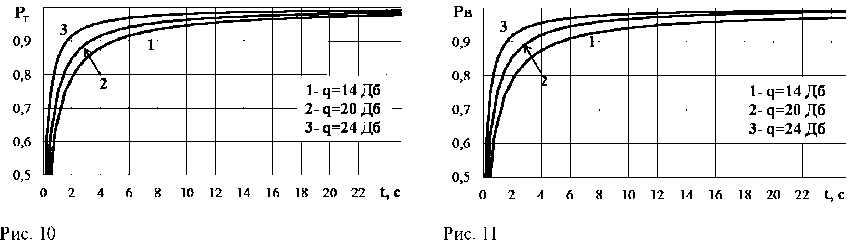
q, дБ Вероятность M[∙] σ[∙] I0,95 14 РС 0,76 0,02 0,75; 0,78 РУ 0,75 0,03 0,74; 0,77 РТ 0,77 0,02 0,75; 0,78 РВ 0,76 0,02 0,75; 0,77 20 РС 0,82 0,03 0,83; 0,85 РУ 0,83 0,02 0,82; 0,84 РТ 0,83 0,02 0,81; 0,84 РВ 0,83 0,03 0,81; 0,85 24 РС 0,91 0,02 0,90; 0,93 РУ 0,9 0,01 0,89; 0,91 РТ 0,9 0,02 0,89; 0,92 РВ 0,91 0,01 0,90; 0,92 для полета с торможением – 0,75…0,92;

для висения – 0,75…0,92.

Таким образом, на основе многомерной линейной дискретной калмановской фильтрации и при частично заданной структуре автоселектора скорости носителя РЛС ВБ был синтезирован алгоритм распознавания режима полета вертолета и получены его точностные и вероятностные характеристики.