Токи внезапного короткого замыкания в синхронном генераторе с магнитоэлектрическим возбуждением

Повышенный интерес в последние годы к возобновляемым источникам электроснабжения (ВИЭ) – ветроэнергоустановкам, мини- и микроГЭС – предопределил увеличение разработок низкоскоростных генераторов мощностью от единиц до 100–150 кВт. Это главным образом асинхронные и синхронные генераторы с возможностью их полной или частичной герметизации, отсутствием скользящих контактов, позволяющим выполнять их необслуживаемыми. В синхронных генераторах с этой же целью применяют магнитоэлектрическое возбуждение.

Особенности работы ВИЭ – мощность источника, соизмеримая с мощностью потребителя, переходные процессы, связанные с постоянным изменением нагрузки потребителя, мощностью приводного движителя, существенно зависящей от скорости ветра или водного потока.

Для свободнопоточной микроГЭС [1] разработан низкоскоростной торцевой синхронный генератор (НТСГ) с возбуждением от постоянных магнитов [2], позволяющий применить прямой привод от ортогональной турбины, вращающейся в свободном потоке с частотой 85– 250 об/мин.

При проектировании этого генератора основная задача расчета магнитной системы машин с постоянными магнитами [3] заключалась в определении конструкции, оптимальной по габаритам, массе, стоимости и другим показателям, обеспечивающей в рабочем зазоре заданное значение магнитного потока. Разработанная математическая модель генератора применима и для расчета других конструкций генера-

В статье представлена разработанная с использованием предыдущей модели математическая модель переходных процессов НТСГ.

В качестве методологической основы вывода уравнений синхронных машин использованы положения об обобщенном электромеханическом преобразователе энергии.

При математическом описании синхронной машины сделан ряд общепринятых допущений [4], которые дают возможность вместо реальной машины с достаточной степенью точности исследовать идеализированную синхронную машину.

В математической модели НТСГ введено еще одно допущение: учет активного сопротивления статора. Поскольку в генераторах малой мощности активное сопротивление соизмеримо с индуктивным сопротивлением и существенно влияет на характер переходных процессов, изменяются следующие параметры: длительность процессов увеличивается, и они становятся затухающими, амплитуда тока возрастает. Перечисленные параметры очень сильно влияют на выбор системы управления, от которой зависит качество стабилизации величины напряжения и его частоты.

В стабилизированных магнитах их магнитные свойства характеризуются внутренней магнитной проводимостью. В соответствии с таким представлением ротор низкоскоростного синхронного генератора с магнитами и полюсными наконечниками заменен эквивалентной обмоткой, состоящей из обмотки возбуждения и стержней демпферной обмотки, подключенными к источнику тока. Такая замена позволяет представить уравнения равновесия напряжений синхронного генератора с постоянными магнитами по аналогии с уравнениями обычной синхронной машины. МДС магнитов представлена магнитодвижущей силой фиктивной обмотки возбуждения, т. е. произведением тока обмотки возбуждения на число витков этой же обмотки. С учетом выбранного числа витков обмотки возбуждения определен ток возбуждения. Аналогично проводится расчет и для демпферной обмотки, при этом задаются количеством ее стержней.

Пусть обмотка статора многофазная (m i > 3) и равномерно распределена по окружности расточки статора. Основная гармоническая МДС этой обмотки распределяется вдоль полюсного деления по синусоидальному закону. Ротор машины явнополюсный, воздушный зазор под полюсным наконечником постоянен. Распределение индукции магнитного поля в воздушном зазоре на полюсном делении τ, создаваемой МДС обмотки статора и постоянными магнитами ротора, определяется проводимостью воздушного зазора.

Обмотки статора и ротора имеют в общем случае разное число фаз и витков, различное распределение в пространстве. Для того чтобы расчеты производились в одной системе координат, выполнено приведение роторной обмотки к статорной с помощью принятых коэффициентов приведения. По условиям приведения полная мощность в реальных и приведенных обмотках должна быть одинакова.

Принимаем, что обмотки возбуждения и демпферная обмотки (ротора) приведены к якорным обмоткам (статора).

Для каждой из обмоток машины можно записать уравнения второго закона Кирхгофа

-ud = dy d/dt - toyq + raid

-uq = dyq/dt + toyd + raiq ufd = dV fd/dt + rfdifd ufq = dV fq/dt + rfqifq

0 = dy 1 d/dt + rx di d

0 = dV ! q^{/dt +} r i q i ! q

Система уравнений (1) может быть ещё дополнена уравнением движения

М В

М+J л > dt

где M_B – внешний вращающий момент, М – электромагнитный момент; J – момент инерции вращающихся масс ротора, ω – угловая скорость ротора.

Дифференциальные уравнения (1), (2) устанавливают связь между напряжениями, токами и потокосцеплениями машины. В них в качестве коэффициентов входят активные сопротивления обмоток якоря, возбуждения и демпферной, индуктивности само- и взаимоиндукции обмоток. Эти электрические параметры необходимы для определения точки отхода прямой возврата и ЭДС холостого хода, зависят от формы магнитного поля в рабочем зазоре и, следовательно, от конструкции ротора. На рис. 1 рассмотрена модель явнополюсного низкоскоростного торцевого синхронного генератора с постоянными магнитами.

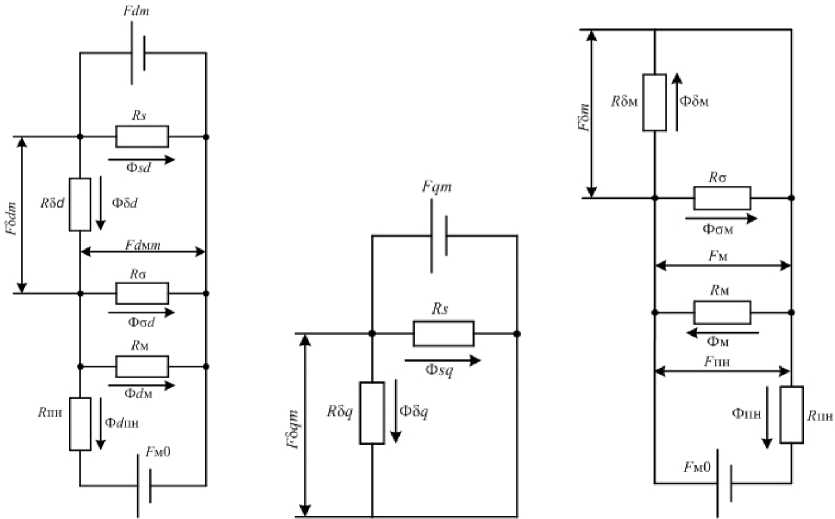
По расчетной модели составлены схемы замещения магнитных цепей для различных положений ротора: в межполюсном пространстве (рис. 2 а ), распределение магнитного поля реакции якоря (рис. 2 б ), распределение магнитного поля магнита (рис. 2 в ).

Каждое сопротивление в схеме замещения – это обратная величина соответствующих магнитных проводимостей, необходимых для определения индуктивных сопротивлений машины x_q, x_d .

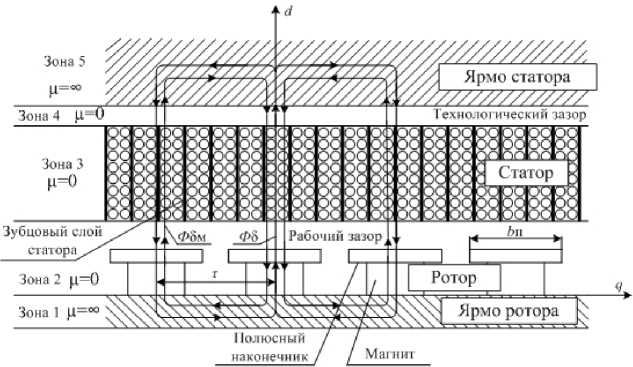
Рис. 1. Расчетная модель явнополюсного генератора

а)                                        б)                                        в)

Рис. 2. Схемы замещения магнитных цепей

Сопротивление воздушного зазора R δ d для потока Ф δ d будет равно

R

F

8 dm _

δ

δ d        0 δ фd d    ^Λ _δd

-

Аналогично находят сопротивление R _{δ d} для потока Ф _{δ d}

R

F

⁸ qm _

δ

δ q        0 δ фq q    ^Λ δq

-

Сопротивление рабочего зазора R δ d для потока Ф δ d будет равно

R

F

δ m

δ м       0 δ фм м

Λ

δм

.

Сопротивление полюса магнита по продольной оси

R м

h

м

м в мм

Λ

м

-

Сопротивление рассеяния якоря

-

Сопротивление рассеяния ротора на один полюс

R- 4

-

Поскольку в синхронных машинах с постоянными магнитами воздушный зазор равномерен и существенно меньше длины полюсной дуги, можно принять, что поле в рабочем зазоре в пределах полюсной дуги для ротора распределено по прямоугольному закону, для статора – по синусоидальному закону, а в промежутках между полюсами равно нулю.

Для исследования переходных режимов в электрических машинах был использован операторный метод. Принимая частоту вращения ротора неизменной, вводя относительное время и переходя от оригиналов переменных функций к их изображениям, систему дифференциальных уравнений (1) можно представить в следующем виде:

-u d ^ = Р ' V_d(P) ^- ®¥ q ⁽P) + r a i d P)

^-u q ⁽P) = Р • ^dV q (P) + ^V d (P) + r a^ P) ^u fdd ^(p) = ^р • ^V fd ^(p) + ^r ffd i ffd ^(p)

q^ =     fq ^(P) + ' < ^P

⁰ = ^PV 1  - + r i A ^Р

⁰ = р "V 1 q^) ⁺ r i q iq»)

где u_d ( p ), u_q(p ), U fd ( p ) - изображения напряжений, приложенных к обмоткам машины; ^(р) - изображения потокосцеплений обмоток машины; i(p) - изображения токов.

Решив систему уравнений (9) относительно токов, после несложных преобразований получим ud(p) •Z4p+u4p • xq(p)+U(p) •

i d ^(p) =

xx p • / ad  >) • Z (P) + /   ad W • x (p)

V ⁺ px_f )     ^q    ( r ^ ⁺ px_f )     q ,

Zd(p) • Zq(p)+xd(p) • xq(p)

u (p ) • x (p) + u (p ) • Z (p) - U (рр. dq q d f

i q (P ) =

p • ( x^ad    ( Pp ) • Z_d(p) - p •

(r + px ) d ff

/ x^ad \ (p ) • x_d(p) ⁽ r_/ + px f. )      ^d _

Z (p) • Z (p) + x (p) • x (p) d q dq

,

где Z_d(p ) = r 1 + p • x_d(p ), Z_q ( p ) = r 1 + p • x_q(p ) - соответственно полные операторные сопротивления синхронного генератора по продольной и поперечной осям.

С помощью теоремы разложения осуществим переход от операторных выражений токов к временным. Определим корни уравнения

F l (p ) = Z d ( p ) • Z q ( p ) + X d ( p ) • X q (p ) = 0-

Так как X d ( p ) и X q (p ) - сложные операторные функции, преобразуем (12) следующим образом:

^F 2 (P) = xd(P) • x q ⁽P) P ^{2 +} P • r I *⁽P) ⁺ x (P) J / 1 V “ q

"

/ 1 x (p) • x (p)Kr / 1 x (p) • x (p) + I I = 0 .

V d ^q ; i v d q 2J

Отношение

2 • X d (p ) • X q (p ) / X d ( p ) + X q ( p ) = X₂(p )

представляет собой операторное индуктивное сопротивление обратной последовательности. Зависимость x ₂( p ) от индуктивных операторных сопротивлений по продольной и поперечной осям обусловлена тем, что магнитное поле обратной последовательности движется относительно ротора с двойной синхронной частотой и его амплитуда поочередно совпадает с осями d и q ротора, т. е. равно x ₂( p ) поочередно равно X d (p ) или X q ( p ). Корни характеристического уравнения (14) находятся приравниванием к нулю индуктивных операторных сопротивлений x d ⁽ p ), x q ⁽ p ) ^и выражений в квадратных скобках.

Корни выражения (13) в квадратных скобках найдем при условии, что переходный процесс затухает, т. е. r_f + 0. Операторные сопротивления x d ( p ) = x' d , x_q(p ) = x_q .

^x 2 (^p) ² • ^x _d • x^q/(xd ^{+ Xq) x} 2 .

Выражение (13) принимает вид

F 2 (p) = x_d(p) . x , (p) ^ p 2 + p . ( 2,,2

+ 1 = 0.

В^{оспользуемс}я выражением операторного индуктивного сопротивления ^X d ⁽ р ) через п^остоянные времени T d и T d о :

где T d 0

xf

– постоянная времени обмотки возбуждения при разомкнутой обмотке статора;

x

d d 0 x

rf d – постоянная времени обмотки возбуждения при замкнутой обмотке статора и d

разомкнутой демпферной.

Приравнивая x d (p ) и выражение в квадратных скобках (17) к нулю, соответственно получим

P 1 =

^, T^' d

p = \ r/x i ² - 1 - r / 1 x x 1 = i .

Вне зависимости от мощности генератора и его полюсности в выражении (20) корень р' _'

равен мнимой единице, так как слагаемые ( г /х г и r²/ 1 х x I для рассматриваемых гене- 12     1 ^ d q )

раторов мощностью до 50 кВт очень малы. Поэтому учет активного сопротивления статора происходит в уравнении (19) только в первом слагаемом.

x

Так как постоянная времени = Т а , тогда r

p23 - - ± p - а

Зная корни характеристического уравнения, по теореме разложения определим оригиналы токов id(τ), iq(τ). После ряда преобразований получим id(т) = -Eo 1 /xd +1 /xd -I/xd )exP(- T/Td )-(1 /xd )eXP(- T/Ta )cosT]            (22)

i q ^{( T} ) = ^- E o 1 ^/X q e^XP ^{( - Т/Т} _а ^{) si}n ^{T ]} -

По разработанной математической модели рассчитаны переходные процессы для низкоскоростного торцевого синхронного генератора мощностью 5 кВт напряжением промышленной частоты 220/380 В и частотой вращения 250 об/мин.

График переходной составляющей тока короткого замыкания будет описываться следующим выражением:

i Кп = I m exp ( - t/T d ) cos _mt ,

'

^где Im = Eo '

f 1

^^^^^^m

\

( xd

xd

– амплитуда переходной составляющей тока короткого замыкания.

График апериодической составляющей токов короткого замыкания представлен на рис. 3.

Из графика (рис. 3) видно, что под влиянием активного сопротивления апериодическая составляющая тока короткого замыкания затухает быстро. Длительность переходного процесса составляет чуть более 0,1 мс, начальная величина равна 2 I н.

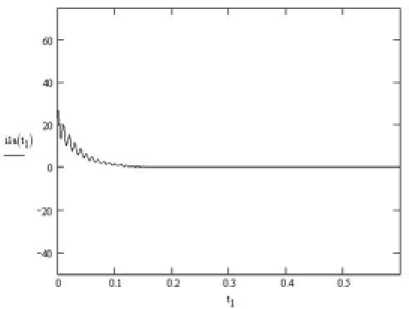
Рис. 3. График апериодической составляющей тока при трехфазном коротком замыкании

Выражение установившегося тока короткого замыкания примет вид ikm = Im cos tot.                                                              (25)

Построив кривые отдельных составляющих и сложив их ординаты, получим результирующую кривую тока короткого замыкания. Тогда выражение для результирующего тока короткого замыкания примет вид ik = Ila (t )-Vm exp(- t/Td)+ Im ]cos tot.                                    (26)

Графики установившегося и результирующего токов короткого замыкания представлены на рис. 4. Амплитуда установившегося тока короткого замыкания равна 2 I н. Установившееся значение тока достигается к 0,1 с.

При коротком замыкании, когда потокосцепление максимальное, результирующий магнитный поток, сцепленный с фазой, можно рассматривать как сумму основного потока и потока самоиндукции, созданного апериодической и периодической составляющими тока короткого замыкания. Поток самоиндукции, создаваемый периодической составляющей тока симметричного короткого замыкания, вращается синхронно с ротором и вызывает появление апериодических токов в обмотке ротора. Поток самоиндукции, создаваемый апериодической составляющей тока короткого замыкания, будучи неподвижным в пространстве, индуцирует ЭДС основной частоты в обмотке вращающегося ротора, в результате чего на апериодические всплески токов в обмотке возбуждения налагаются периодические токи основной частоты. В результате сложного процесса взаимодействия апериодических токов статора (рис. 3) и периодического тока ротора кратность токов в обмотках дополнительно возрастает. При этом если апериодическая составляющая тока в обмотке роторе затухает с постоянной времени T' d , то периодическая составляющая тока (рис. 3) затухает с постоянной времени T_a обмотки статора.

Магнитная проводимость ротора также отличается по продольной и поперечной осям. Вследствие этого суммарный ток короткого замыкания (рис. 4 б ) стремится поддержать неизменным потокосцепление, испытывает колебания и изменяется во времени так, как показано на рис. 4 б . При x q = x d пульсации апериодического тока практически отсутствуют.

Полученные данные показывают, что пульсирующие составляющие момента, возникающие в результате взаимодействия магнитных потоков, движущихся относительно друг друга, весьма велики и стремятся отогнуть лобовые части обмотки статора. Кроме того, в начальный момент короткого замыкания машина испытывает сильный удар, поскольку энергия магнитных полей в этот момент значительно возрастает за счет кинетической энергии ротора. В результате этого возникает тормозящий момент, имеющий характер кратковременного импульса. Следовательно, большое внимание должно уделяться обеспечению механической прочности машины, прежде всего ее активной части.

В торцевом генераторе обмотки, выполненные в виде обмоточных модулей, заливают компаундом, создавая изоляцию типа «монолит», улучшающую изоляционные свойства обмотки, ее теплоотдачу и повышающие механическую прочность статора.

Постоянные магниты ротора устанавливают в специальный шаблон, исключающий их взаимное перемещение, и закрывают полюсными наконечниками, закрепляемые немагнитны- – 927 –

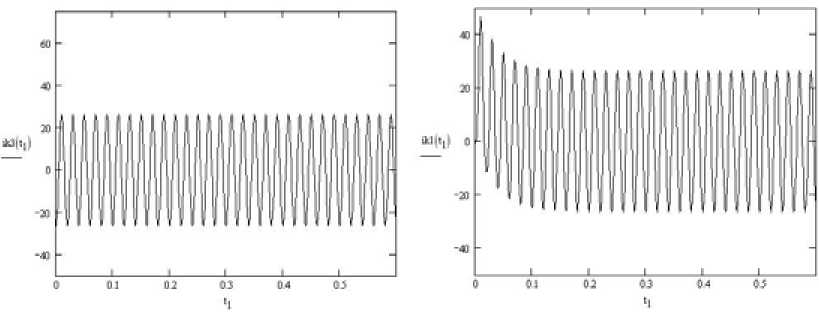
а)

(б)

Рис. 4. Графики установившегося ( а ) и результирующего токов короткого замыкания ( б )

ми винтами на диске ротора за пределами активной части. С учетом амплитуд знакопеременных моментов рассчитываются вал и подшипниковые щиты генератора.

Процесс внезапного короткого замыкания, происходящего при работе машины под нагрузкой, имеет более сложный характер, но в главнейших чертах аналогичен рассмотренному выше случаю, когда короткое замыкание происходит при холостом ходе. Величины начальных и ударных токов короткого замыкания при этом также существенно не изменяются.