Тонкая круговая пластина под действием равномерно распределенной нагрузки гравитационного типа

В авиационной, ракетной, кораблестроительной и других областях промышленности всегда большое внимание привлекают проблемы устойчивости и колебаний различных конструкций: оболочек, мембран, стержневых систем и т. д.

Гибкие пластины и оболочки являются типовыми элементами микроэлектромеханических систем, применяемых в устройствах исполнительной автоматики космических аппаратов. Задача об устойчивости оболочек наряду с задачей об изгибе стержней являются всегда актуальной проблемой механики деформируемого твердого тела.

В работах [1–3] даётся общая методика исследования задач изгиба оболочек. В работах [4] и [5] методом стрельбы решается задача изгиба круглой мембраны при радиальном сжатии. В работе [6] решение задачи о радиальном сжатии круглой пластины решается в аналитическом виде. Работа [7] посвящена численному анализу задачи об изгибе круглой мембраны из ферроэласта в однородном магнитном поле. В настоящей работе предметом исследования является изгиб тонкой круговой пластины под действием равномерно распределенной поперечной нагрузки постоянного направления.

Исследование изгиба круговой пластины под действием гравитационной нагрузки. Рассмотрим круговую пластину под действием распределенной нагрузки, направленной перпендикулярно её плоскости и сохраняющей свое направление. Для записи уравнений равновесия используем цилиндрическую систему координат, как показано на рис. 1.

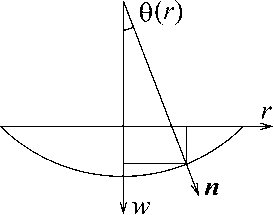
Рис. 1. Система координат

Исследование проводится в геометрически нели нейном случае, то есть — = cos 0 , где r - радиальная dl координата, l – криволинейная длина, отсчитываемая от оси w, 0 - угол наклона касательной к полярной оси.

В заданной системе координат система уравнений равновесия сил и моментов будет выглядеть следующим образом

ГF

rd ( ^F- F- = ⁰

) = q                                , (1)

d0

( rM ) M = - F sin 0 + F cos 0

r dF   r) r p r z где Fr – погонная (на единицу длины) сила в радиальном направлении, F, - погонная трансверсальная сила, Fz – погонная сила в аксиальном направлении, q = const – поверхностная плотность внешней распределенной нагрузки, Mr и Mр - соответственно погонные радиальный и трансверсальный изгибающие моменты.

Преобразуем третье уравнение системы (1). Для этого применим закон Гука для линейно упругого материала

Mr = D (к r 1 цк J , M 9= D (s+ЦК r ) ,

где D = Eh ³/12 ( 1 -ц ) – цилиндрическая жесткость; h – толщина пластины; R – радиус; E – модуль Юнга; ц - коэффициент Пуассона; к _r и к , - соответственно главные радиальная и трансверсальная кривизны изогнутой поверхности пластины. Далее, учитывая соотношения для кривизн

_Л d 0         sin 0

к r = cos 0 —, кр=--- dr r к r +кр = 1 d ( r sin 0), rdr получаем cos 0 d rdr

F

(rFr )-^ = 0 r

cos 0 d rdr

( ^rF z ) = q

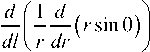
- F_r sin 0 + F_z cos 0

Интегрируя первые два уравнения системы (2), имеем

F r = 1J F , dl + C rr

F = 1 r qrdr + C 2 . ^z r^ cos 0 r

Подставим (3) в третье уравнение системы (2), вынося общий множитель 1/ r за скобки, получим

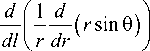
.       . . (4)

C ₂ | cos 0 .

¹ [- (J F , dl + C i ) sin в + fj qrdr + r L ^XJ ’ v cos 0

При отсутствии внешней нагрузки, сосредоточенной по краю, в пластине в точке r = R усилия равны 0, значит F r ( R ) = 0 и F z ( R )= 0, поэтому C 1 = 0 и C 2 = 0. Используем следующее стандартное выражение для трансверсальной силы и соотношение между радиальным и трансверсальным продольными напряжениями

F p = h Q , ,

Q

,

A d I rGr cos 0—I —— dr I cos 0

Радиальное напряжение направлено вдоль касательной, поэтому, как видно из рис. 1

q _r = q sin 0 ,

Q, = qd(r tg0), j F, dl = j hqd^ (r tg 0) dl = hq j -dl (r tg 0) dl = hqr tg 0. Подставляя полученное выражение в (4), получаем, учитывая, что dr = cos 0dl d (1 d / . ^x) 1 Г 7      2 p qrdr

D — I--(r sin 0)| = — -hqr tg2 0+ ---- dr V r dr ) r L            J cos 0

Раскрывая скобки в левой части уравнения (5), получим интегро-дифференциальное уравнение

D d ² sin 0 dr ²

1 d sin 0

+ D-- rdr sin 0 7     2 м 1 f qrdr

- D^ + hqr tg ² 0 = -J L .

r ²                 r cos 0

Построим далее приближенное аналитического решение нелинейного уравнения (6) в предположении малости прогиба пластины. Будем считать, что угол наклона касательной 9 изменяется очень медленно, следовательно, cos9 под знаком интеграла мало отличается от 1. В свою очередь, r меняется от 0 до R, тем самым определяя поведение подынтегральной функции. Поэтому в интегральном члене можно воспользоваться теоремой о среднем и положить cos9 = 1. После такого упрощения мы получим дифференциальное уравнение

„ d ² sin 9 „1 d sin 9 sin 9 ,    . qr

D----— + D---D —— + hqr sin2 9 = —, dr2rdr r22

или, объединяя первые два слагаемых, получим

„ 1 d ( d sin 9) sin 9 ,     -г „ qr

D--r ----- - D —— + hqr sin ² 9 = — . (7)

r dr ( dr J      r ²                 2

Уравнение имеет ядро r и, следовательно, особую точку при r = 0. Поэтому в центре пластины ставится условие ограниченности решения.

Обезразмерим уравнение (7), произведя замену x = r / R, имеем d sin 9)       sin 9 hqx sin2 9 qx

- DR2—+        =   , dx J       x2      R 2 R

' sin 9) sin 9 hqx sin2 9= qx dx J   x2     DR3   " 2 DR3"

DR ’ ' — | x x dx V

1 d f d

—-I xx dx V

Введем новый безразмерный параметр нагрузки k ≡ q /( DR ³), тогда уравнение преобразуется к виду

1 d f d sin 9) sin 9 ,, . ₂ k --I x ------I--— + hkx sin 9 = —x .

x dx V dx J x2

Граничные условия при жестком закреплении по контуру имеют вид

19(0)| <«,     9(1) = 0(9)

Так как прогиб пластины мал, можно считать, что sin 9 >> sin2 9 . Из того, что 0 < x < 1, следует sin9

—— >> hkx sin 9 ,   значит,   можно положить x2

hkx sin ² 9 = 0, тогда уравнение (8) приводится к виду

1 d f d sin 9) sin 9 k --I x------I--— = —x, x dx V dx J x2

19 ( 0 )| <« ,       9 ( 1 ) = 0.

Обозначая для простоты записи sin(9(x)) = y (x), и раскрывая скобки, получаем линеаризованное уравнение x2 y" + xy'- y = 2 x3.(10)

Решение его найдем методом вариации произвольных постоянных, для этого решим однородное уравнение, соответствующее (10)

x2 y" + xy ‘ - y = 0.(11)

Решение его пишется сразу y = C1 x + -2-.(12)

x

Считая C 1 и C 2 зависящими от x , подставим (11) в (9), тогда получаем систему уравнений

CLCL к

c;x+11 = 0, c;—2 = -x.(13)

1x           1x2

Разделим первое уравнение (13) на x и сложим со вторым, затем умножим второе уравнение на – x и сложим с первым. Получим

C2=- 4 x3, C‘= 4 x.(14)

Следовательно,

C2 =- kx4 + C20, C1 = kx2 + C10.(15)

Подставляя (15) в (10), имеем окончательно sin 9 = C10x + ^2° + — x3.

10 x 16

Ввиду первого граничного условия (9), С ₂₀ = 0.

Применяя второе условие (9), получаем к

C 10 =-    .                     (17)

Тогда sin 9 = 1k (x3 - x).                   (18)

Криволинейная длина и прогиб определяются по формулам rdr

I                   , w

0 1 - - sin ² 9 ( r )

R sm- ⁹⁽ r ) dr . ₍1₉₎ r 1 - - sin ² 9 ( r )

С учетом (17), выражения (18) принимают вид

x

l ^{( r} ) = J

w ^{( r} ) = ^- J

x

dx

1 - k 1² ( x ³ - x ) ² , k 1² ( x ³ - x ) dx у/ 1 - k 1² ( x ³ - x ) ²

.

Здесь введено обозначение k 1 = k /16. Построенное решение (20) соответствует первой моде статического нагружения пластины.

Из условия неотрицательности подкоренного выражения в интегралах (20) следует, что максимальное значение k 1 ® 2,5. Так как в данной работе рассматривались малые прогибы, то мы ограничились значениями k 1 < 1. При этом прогиб не превосходит значения 0,1.

Формы изогнутой пластины приведены на рис. 2. Величина внешней нагрузки q , геометрические и физические параметры пластины и параметр k 1 связаны соотношением 16 k 1 = q /( DR ³)

Построенные решения качественно совпадают с численными решениями Л. И. Шкутина и уточняют известные приближенные аналитические решения [1–3].

В работе проведено исследование изгиба тонкой круговой пластины, находящейся под действием постоянной равномерно распределенной нагрузки гравитационного типа. При условии малости величины прогиба по сравнению с радиусом самой пластины построено уточненное приближенное аналитическое решение поставленной задачи с учетом геометрической нелинейности.

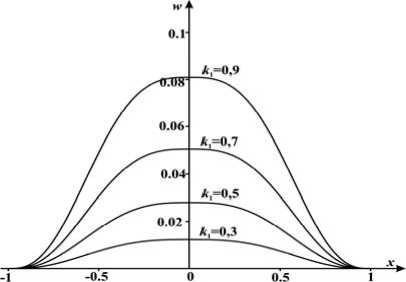
Рис. 2. Формы изгиба тонкой круговой пластины при различных значениях безразмерной нагрузки k ₁. Масштаб по осям 1:10