Топологическая оптимизация силовых конструкций на основе модели переменной плотности

[3] объяснили эти особенности тем, что в любой точке допустимой геометрической области с учетом дискретности используемых математических моделей реализуется одно из двух возможных «крайних» состояний: конструкционный материал либо содержится, либо отсутствует. Для устранения указанных недостатков в постановке задачи структурной оптимизации силовых конструкций предложено использовать специфические пористые материалы. При этом в геометрические ограничения, внутри которых может размещаться конструкция, вписывается непрерывная упругая среда (континуальная модель), включающая в себя все возможные силовые схемы. Результаты оптимизации параметров континуальной модели могут дать информацию о наилучшей силовой схеме разрабатываемого объекта. Такой подход, использующий твердое деформируемое тело с переменными по объему характеристиками материала, допускает возможность появления в модели конструкции «переходных» зон между «крайними» вариантами состояния упругой среды.

Отметим, что ранее в работе Комарова А.А. [4] высказана и использована идея применения в процессе проектирования конструкций гипотетического материала с переменным по объему модулем упругости при оптимизации плоских конструкций. В дальнейшем эта идея получила развитие в исследованиях [1, 3, 5-8] в виде тела переменной плотности с соответствующими прочностными и упругими характеристиками. Bendsoe M.P. и Kikuchi N. [5] решили задачу оптимизации распределения материала в континуальной модели относительно степени пористости материала. В этом исследовании упругая среда, вписанная в допустимую геометрическую область, делится на конечные элементы. За целевую функцию принимается податливость упругой среды, а ограничением является масса материала. Материал упругой среды считается пористым, для чего ему сопоставляется определенная микроструктура. Элементарная ячейка такой микроструктуры для пластины показана на рис. 1. В ячейке имеется полость прямоугольной формы с длинами сторон a и b. Размеры полости внутри ячейки определяют общую пористость материала или долю незаполненного в нем объема. Каждый конечный элемент имеет фиксированное значение пористости. Размеры полостей ai и bi и ориентация ячеек θi рассматриваются как переменные проектирования, где i – номер элемента. Изменение размеров полости и угла ее ориентации влечет за собой изменение свойств материала упругой среды, определяемых методом усреднения (homogenization method) [5, 6]. Свойства материала упругой среды в случае проектирования пространственной конструкции определяются пятью проектными переменными в каждом элементе [6, 7].

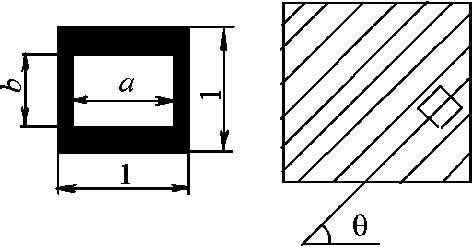
Рис. 1. Размеры и ориентация элементарной ячейки

В монографии [6] отмечается, что при проектировании тонкостенных конструкций топологическая оптимизация по методу усреднения обычно приводит к получению стержневых конструкций типа ферм Мичелла [9]. В то же время, например, большинство авиационных конструкций по своей природе являются тонкостенными упругими системами, состоящими из элементов, обладающих различными свойствами. Так, лонжероны, нервюры и шпангоуты обычно состоят из поясов, адекватно моделируемых стержневыми элементами, и стенки, работающей в плоском (мембранном) напряженном состоянии. Обшивка часто подкрепляется стрингерным набором для увеличения критических усилий потери устойчивости. Следовательно, для эффективного проектирования силовых схем авиационных конструкций решения, получаемые на континуальной модели, должны обосновывать выбор не только стержневых, но и оболочечных элементов.

Для целей топологической оптимизации авиационных конструкций Комаровым В.А. [1] введен в рассмотрение изотропный материал с переменной плотностью ρ , модуль упругости и прочностные характеристики которого пропорциональны плотности

E = ρ E , (1)

σ = ρσ , (2)

где σ – допускаемое напряжение материала; E и σ – модуль упругости и допускаемое напряжение при единичной плотности.

Допустимое геометрическое пространство конструкции разбивается сеткой трехмерных конечных элементов, моделирующих объемное напряженное состояние, и плотности материала в элементах принимаются за переменные проектирования. Особо отметим, что в каждом элементе упругой среды (1) – (2) используется только одна проектная переменная. Эта особенность, с одной стороны, позволяет строить более эффективные алгоритмы оптимизации распределения материала в континуальной модели по сравнению с подходом [5], с другой стороны, предъявляет повышенные требования к процедурам интерпретации получаемых результатов, в том числе к анализу силовой работы среды переменной плотности.

В работе [1] обоснован выбор приближенного алгоритма с использованием концепции полнонапряженности. В [8] этот подход обобщен на случай одновременного учета ограничений на эквивалентные напряжения, обобщенные перемещения и критические усилия потери устойчивости. Вариации проектных переменных в соответствии с алгоритмами [1, 8] вырождают элементы, передача усилий через которые нерациональна, и, наоборот, выделяют из конструкции элементы, обеспечивающие рациональные пути передачи сил. В результате определяется теоретически оптимальная конструкция (ТОК). В [1] разработана методика выбора рациональных силовых схем конструкций типа крыла с использованием картин потоков главных усилий (ПГУ) главных касательных сил (ГКС) с учетом конструктивных и технологических требований.

Идеи, высказанные в [1], могут быть использованы и развиты для проектирования произвольных пространственных тонкостенных конструкций. Стратегия выбора рациональной силовой схемы конструкции на основе интерпретации силовой работы тела со свойствами материала (1) – (2) заключается в следующем:

• 1.    Для удобства анализа силовой работы континуальная модель делится на ряд слоев объемных конечных элементов.

• 2.    Первое приближение к выбору рациональной структуры синтезируемого объекта может дать информация о расположении в ТОК сгустков плотности и зон с «разреженной» плотностью (а, следовательно, и с незначительной жесткостью). Граница между вырожденными и невырожденными элементами определит контур силовой части проектируемой упругой системы. Если эта граница не является чётко выраженной, то далее целесообразно прорабатывать несколько вариантов структуры конструкции.

• 3.    Принимая во внимание достаточно малые размеры конечных элементов континуальной модели, полагаем, что компоненты тензора напряжений внутри элементов изменяются незначительно. Поэтому для идентификации основных путей передачи усилий в ТОК анализируются значения напряжений и усилий в центре элементов.

• 4.    Послойная визуализация распределения материала и ПГУ позволяет выявить зоны ТОК, в которых материал работает в существенно одноосном или двухосном напряженном состоянии [1]. В силовой схеме разрабатываемой конструкции в этих зонах целесообразно использовать, соответственно, стержни и оболочки.

• 5.    Для уточнения формы и расположения оболочек можно использовать картины ГКС в различных проекциях ТОК.

• 6.    Элементы, предназначенные для подкрепления оболочек, целесообразно располагать в соответствии с картинами ПГУ, стремясь к тому, чтобы направления стержней были близкими к направлению одного из главных усилий на соответствующем участке.

Рассмотрим особенности анализа ГКС в случае пространственных конструкций. В произвольном элементе серединного слоя ТОК вырежем кубический элемент с гранями единичной длины, параллельными координатным осям (рис. 2).

Со стороны рассматриваемого элемента на единичную площадку смежного элемента, нормальную оси x , действуют касательные силы τ xy и τ xz , равные касательным напряжениям. Заменим силы τ xy и τ xz равнодействующей τ x . ГКС τ x можно изображать как векторы без стрелок в центре элементов на схеме соответствующего слоя модели в перпендикулярной оси x проекции. Траектории ГКС в ТОК позволяют выявить рациональные сечения предполагаемых оболочек. Аналогичные картины ГКС τ y и τ z можно построить в проекциях, перпендикулярных осям y и z .

Рис. 2. Единичный кубический элемент континуальной модели произвольной пространственной конструкции

В качестве примера визуализации ГКС рассмотрим призматический стержень с квадратным поперечным сечением, защемленный по одному торцу и нагруженный крутящим моментом по свободному торцу. Для стержня, заполненного материалом переменной плотности, по алгоритму [1] получена ТОК. На рис. 3 показано распределение материала и траектории ГКС в продольном и поперечном сечениях ТОК.

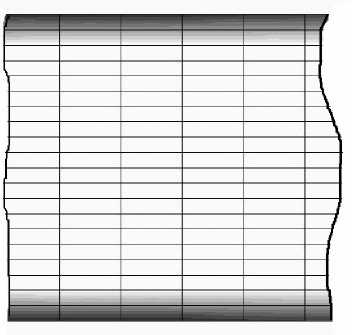
Выводы: картины распределения плотности, ПГУ и ГКС в континуальной модели объекта, составленной из ряда слоев объемных конечных элементов, позволяют наглядно визуализировать и интерпретировать особенности силовой работы пространственных тонкостенных конструкций с учетом их геометрических форм и граничных условий.