Топологическая транзитивность косых произведений в плоскости с отрицательным шварцианом семейства отображений в слоях
Автор: Ефремова Людмила Сергеевна, Фильченков Андрей Сергеевич
Журнал: Труды Московского физико-технического института @trudy-mipt
Статья в выпуске: 4 (16) т.4, 2012 года.
Бесплатный доступ
Выделен класс косых произведений отображений интервала с отрицательным швар- цианом семейства отображений в слоях. Доказан критерий различения топологически транзитивных отображений из выделенного класса, основанный на использовании свой- ства равномерной аппроксимируемости фазового пространства периодическими орби- тами. Построен новый пример косого произведения-эндоморфизма в замкнутом пря- моугольнике, имеющего аттрактор с непустой внутренностью.
Косое произведение, топологическая транзитивность, аттрактор
Короткий адрес: https://sciup.org/142185880
IDR: 142185880
Текст научной статьи Топологическая транзитивность косых произведений в плоскости с отрицательным шварцианом семейства отображений в слоях
Свойство топологической транзитивности является основополагающим при исследовании динамических систем (см., например, [1] - [3]). В последнее время активно изучается свойство робастной (т.е. сохраняющейся при малых возмущениях в пространстве рассматриваемых систем) транзитивности на. компактных многообразиях без края (см., например, [4]). Изучению некоторых робастных свойств на. инвариантных частично гиперболических множествах С 2-диффеоморфизмов, заданных на многообразиях размерности > 3, посвящена, статья [5].
Существует обширная библиография, посвященная различным аспектам топологической транзитивности динамических систем класса косых произведений (см., например, [2], [3], [7], [8]).
Настоящая работа, является продолжением статей [9] и [10], в которых выделен класс топологически транзитивных косых произведений, заданных на. прямоугольнике, и установлена. взаимосвязь свойства, топологической транзитивности отображения из выделенного класса, с наличием всюду плотного (в фазовом пространстве) множества, периодических точек. В отличие от традиционно рассматриваемых обратимых динамических систем (см. также [1] - [7]) все отображения из класса, выделенного в данной работе, являются эндоморфизмами (т.е. необратимыми отображениями).
Определение 1.1 [6]. Пусть X — топологическое пространство. Отображение р : X ^ X называется топологически транзитивным, если существует такая точка жо G X, что её траектория О^(ж) = pn(x)nEN плот на в X. При этом точка с плотной траекторией называется транзитивной точкой отображения р.
Напомним, что отображение р : X ^ X топологически транзитивно тогда и только тогда, когда для любых двух непустых открытых подмножеств U,V С X существует такое натуральное число п = n(U, V ), что V П pn(U ) = 0 [6].
В данной статье определено понятие шварциана семейства, отображений в слоях косого произведения отображений интервала, выделен класс косых произведений в плоскости с отрицательным шварцианом семейства отображений в слоях, доказан критерий различения топологически транзитивных косых произведений из выделенного класса, основанный на. использовании свойства, равномерной аппроксимируемости фазового пространства, (прямоугольника) периодическими орбитами. Полученные результаты позволили также построить новый пример косого произведения-эндоморфизма, в замкнутом прямоугольнике, имеющего аттрактор с непустой внутренностью (ср., например, с [И]).
Косым произведением Ғ : І ^ I, где І = Іі х І2, Іі = [аі,Ьі], І2 = [02,^2], называется отображение вида
Ғ (ж, у) = (f (ж), дх(у'У), где дх(у) = д(ж, у), (1)
при этом f : Іі ^ Іі называется фактор-отобраясонном косого произведения Ғ. а отображение дх : І2 ^ І2 при любом ж € Іі называется отображением, действующим в слое над тонкой ж.
В силу (1) при любом натуральном п справедливо
Ғ п(ж, у) = (f п(ж), Ух,4уҮ), где дх,п(у) = д/п-дх) ° ... ° д/(х) ° дх (у). (2)
Символом дх будем обозначать отображение дх,п, если ж - периодическая точка f (ж € Per(f )) с (наименьшим) периодом п.
Обозначим через Т 3(І) (То(І)) пространство С 3-гладких (непрерывных) отображений вида (1) с фазовым пространством І, наделённым С 3-нор мой (С0- норм ой). В Т 3(І) выделим подмножество отображений, удовлетворяющих следующим условиям:
(С.1) шварциан семейства отображений в слоях, определенный в силу следующего равен ства
S (дх(у)) =
Цз дх (У) д^ дх(у)
-
з / др дх(у) У
2 1м)
отрицателен при всех (ж, у) € І таких, что ддх (у) = 0;
(С.2) отображение дх : І2 ^ І2 при любом ж € Іі имеет не более одной критической точки в интервале (a2,b2), причём эта точка неплоская1',
(С.3) дх (Э (І2)) С Э (І2) при л юбом ж € Іі, г де д (І2) — границ а отрезка І2.
Обозначим через Т3(І ) класс отображений из Т 3(І), удовлетворяющих условиям (С.1) -(С.3).
В настоящей работе построен пример косого произведения из класса Т3(І).
Определим понятие равномерной аппроксимируемости фазового пространства І периодическими орбитами.
Пусть P — произвольное разбиение замкнутого прямоугольника І координатными прямыми на m замкнутых подпрямоугольников J р любые два из которых либо не пересека-m ются, либо имеют общую вершину или общую сторону (при этом І = U Jj).
1=1
Определение 1.2. Будем говорить, что фазовое пространство І отображения Ғ равномерно аппроксимируется периодическими орбитами, если для любого е > 0 и любого разбиения P прямоугольника І с параметром Х(Р ) < е найдётся Ғ-периодическая орбита Orbp (ж;у), пересекающаяся с внутренней частью прямоугольника Jj при каждом 1 < j < m.
Сформулируем основные результаты работы.
Теорема А. Для отображения Ғ € Т3(І ) следующие утверждения эквивалентны:
(А.1) Ғ топологически транзитивно;
(А.2) фазовое пространство І равномерно аппроксимируется периодическими орбитами косого произведения Ғ.
Определение 1.3. Правосторонним (левосторонним) неустойчивым многообразием периодической точки жо периода п отображения f : Іі ^ Іі называется множество
W+ (жо, fп) = {ж € Іі | V U +(жо) 3k € N : ж € f kn(U +(жо))} ,
(W-(жо,fп) = {ж € Іі | V U-(жо) 3k € N : ж € fkn(U-(жо))}) , где U + (жо) — произвольная правосторонняя окрестность точки жо (U-(жо) — произвольная левосторонняя окрестность точки жо).
Введём дополнительное условие:
(С.4) у отображения Ғ Е T3(I ) сунірствуст точка (жо,уо) Е Per(F ) ( наименьшего) периода п такая, что:
-
а) если жо Е IntIi, то W+ (жо, / k ) = Ii, W - (жо,/ k ) = Ii, где k — период точки жо относительно / (k — делитель п), Int0 — внутренность множества;
-
Ь) если жо = ai (или жо = bi), тогда W“(жо,/ k ) = Ii ( W "(жо,/ k ) = Ii).
Теорема В. Пусть Ғ Е T3(I ) удовлетворяет дополнительному условию (С.4). Тогда каждое из условий (М.1) и (М.2) эквивалентно условию:
(В.1) мпооісестоо Per(F) периодически.!: точек отображения Ғ всюду плотно в I.
2. Предварительные сведения
Сформулированные теоремы проясняют природу топологической транзитивности отображений из T3(I): топологическая транзитивность здесь равносильна возможности равномерно аппроксимировать фазовое пространство рассматриваемой динамической системы её периодическими орбитами с любой наперёд заданной степенью точности.
Статья построена следующим образом. Во втором разделе приведены вспомогательные сведения, использующиеся в работе. Третий раздел посвящён доказательству основных теорем А и В; здесь приведён пример, показывающий, что условие (С.4) в теореме В опустить нельзя. В четвёртой части работы построен пример косого произведения в замкнутом прямоугольнике, имеющего глобальный аттрактор с непустой внутренностью.
Приведём ряд утверждений, устанавливающих взаимосвязь свойства топологической транзитивности отображения из класса T3(I ) со свойствами его фактор-отображения и отображений в слоях.
Заметим, что фактор-отображение произвольного непрерывного топологически транзитивного косого произведения на отрезке Ii сюръективно, топологически транзитивно и имеет плотное множество периодических точек.
Лемма 2.1. Пусть Ғ Е T3(I) удовлетворяет условию (М.1). Тогда при любом ж Е Ii отображение д ж (у) унимодально по у2.
Доказательство. В силу условий (С.2) — (С.3) возможны следующие случаи:
-
(а) каково бы ни было ж Е Ii, дж (у) не содержит критических точек как функция переменной у;
-
(Ь) существует ж Е Ii такое, что дж(у) содержит критическую точку как функция переменной у.
В случае (а) имеем: каково бы ни было ж Е Ii, дж(у) не содержит критической точки как функция переменной у. Тогда при любом ж Е Ii дж(у) как функция переменной у. является строго монотонной, причем характер монотонности не зависит от ж. Следовательно, для любой точки (ж; у) Е I при условии, что у Е д (I2), выполнены неравенства дж(у) < дж, 2 (у) < ... < дж,„(у) < ... или дж(у) > дж, 2 (у) > ... > дж,„(у) > ... Поэтому найдется уо Е I2 (уо = уо(ж)) такое, что уо = lim дж,п(у). Последнее противоречит топологической транзитивности F. Следовательно, реализуется случай (Ь).
Тогда найдется ж’ Е Ii такое, что дж‘ (у) как функция переменной у содержит критическую точку сж’ Е (а2, 62). В этом случае при у < сж‘ верно неравенство ддж‘(у) > 0, а при у > сж‘ - неравенство !^дж‘(у) < 0. Следовательно, дж‘(у) унимодально по у, и в силу условия (С.3)
9х‘ («2) = 9х‘ (Ы = «2. (3)
Так как функции 9х(«2) и 9^(62) непрерьшны по ж € /1, то из равенств (3) и условия (С.3) следует, что 9х(«2) = 9х(Ь2) = «2 при всех ж € /1. Тогда, используя классическую теорему Ролля и условие (С.2) теоремы, получаем, что при каждом ж € /1 существует единственная критическая точка сх по переменной у отображения 9х(у) при чем сх - точка возврата 9х(у) и 9х(12) = [«2, 9х(сх )]• Лемма 2.1 доказана.
Отметим, что операция композиции (использующаяся при переходе к итерациям отображения Ғ) выводит из класса унимодальных отображений в слоях, приводя к мультимодальным отображениям. При этом знак шварциана отображений в слоях при переходе к их композициям сохраняется (см. [12, гл. 4, § 1]).
Лемма 2.2. Пусть Ғ € Т 0(/) топологически транзитивно. Тогда отображение Ғ — сюрвекуия слоя {ж} х /2 на слой {/(ж)} х /2, при любом ж € 11.
Напомним определение топологической эквивалентности отображений, которое нам потребуется в дальнейшем.
Определение 2.3 [6, ч. 1, гл. 2, § 2.1, п. 2.1а]. Говорят, что отображения 91 : М ^ М и 92 : N ^ N (М и N — произвольные отрезки числовой прямой) топологически эквивалентны, если существует гомеоморфизм һ : М ^ N, что 91 = һ-1 о 92 о Н.
Важную роль в теории унимодальных (мультимодальных) отображений отрезка играет понятие комбинаторной эквивалентности, выделяющее унимодальные (мультимодальные) отображения, всевозможные (соответствующие) итерации которых имеют «одинаковую схему складок».
Определение 2.4 [14, гл. 6, п. 6.1.3]. Говорят, что мультимодальные (унимодальные) отображения 91,92 : /2 ^ /2 с множествами точек возврата С (91) и С (92) соответственно3 комбинаторно-эквивалентны, если существует сохраняющая ориентацию биекция һ : U 91 (С(91)) ^ U 92 (С(92)) такая, что һ о 91(2) = 92 о h(z) при всех 2 € U 91 (С(91)) nEZ nEZ nEZ
И һ(С(91)) = С (92). здось Z - множество целых чисел.
Предложение 2.5 [9]. Пусть Ғ € Т3(/ ) удовлетворяет условию (А1). Тогда при всех ж € /1 и п > 1 отображение 9х,п(у) : /2 ^ /2 комбинаторно-эквивалентно отображению 92 : /2 ^ /2, г Де 9а (у) = А(у — «2)(Ь2 - у)4 при А = (^2—22Д-
Предложение 2.5 показывает, что в рассматриваемом классе косых произведений существует единственное отображение (9д(у)), произвольные итерации которого определяют «схему складок» всех отображений в слоях произвольных соответствующих итераций косого произведения Ғ .
Необходимо отметить, что комбинаторная эквивалентность унимодальных (мультимодальных) отображений отрезка является более слабым свойством, чем топологическая эквивалентность. Из комбинаторной эквивалентности совсем не следует топологическая эквивалентность. Таким образом, комбинаторно-эквивалентными могут быть два унимодальных (мультимодальных) не являющиеся топологически эквивалентными отображения, одно из которых содержит периодические аттракторы, а другое - нет.
Далее будет приведено утверждение (предложений 2.8), указывающее на взаимосвязь комбинаторной эквивалентности с топологической. В начале приведем два вспомогательных определения.
Определение 2.6 [14, гл. 6, п. 6.1.3]. Пусть отображение отрезка / в себя 9 : / ^ / имеет периодическую точку у* (наименьшего) периода п. Периодическая орбита ОтЬд(у* = {у*,9(у*),...,9п-1(у*)} называется периодическим аттрактором периода п. если множество
В (у*) = |ж : 9к (ж) ^ ОтЬд (у*), к ^ +то} содержит окрестность (возможно, одностороннюю) орбиты ОгЬд (у*). Множество В (у*) называют областью притяжения орбиты ОгЬд(у*)
Определение 2.7 [14, гл. 6, п. 6.1.3]. Рассмотрим отображение отрезка I в себя g : I ^ I. Тогда интервал J С I называется блуждающим интервалом, если все его итерации J,g(J),g2(J ),... попарно не пересекаются и последовательность {gn(J )}п>о не стремится к периодической орбите.
Предложение 2.8 [14, гл. 6, п. 6.1.3]. Пусть gi, g2 : I2 ^ I2 — унимодальные (мультимодальные) отображения. Если gi и g2 комбинаторно-эквивалентны и не имеют блуждающих интервалов и периодических аттракторов, то gi и g2 топологически эквивалентны.
Лемма 2.9 [15, гл. 4]. Пусть отображение g Е С 2 (I2) имеет неплоскую критическую точку. Тогда g не имеет блуждающих интервалов.
3. Доказательство основных теорем А и В
Доказательство теоремы А разобьем на ряд шагов, проделанных в леммах 3.1 и 3.5. Для доказательства теоремы В, кроме того, необходимы леммы 3.2, 3.3, 3.4 и 3.6.
Используя критерий топологической транзитивности (см. введение), докажем, что свойство равномерной аппроксимируемости фазового пространства косого произведения его периодическими орбитами влечет за собой топологическую транзитивность косого произведения.
Лемма 3.1. Пусть F Е T3(I ) удовлетворяет (А.2) Тогда косое произведение F топологически транзитивно.
Действительно, возьмём в I два произвольных открытых непустых подмножества U и V. Воспользуемся свойством равномерной аппроксимируемости прямоугольника. I периодическими орбитами отображения F Е T3(I). Найдётся некоторое разбиение Р‘ прямоуголь-к пика I па. к 'замкнутых подирямоуго.тышков (I = U Ij) 11 натуральные числа. 0 < q,р < к г=1
такие, что U D Ig. V D Ip. При этом существует F — перво динеская топка (х*,у*) такая, что FТ (х* ,у*) Е U. a F /(х*,у*) Е V. Для определённости будем считать, что г < I. Тогда Fl-r(U ) П V = 0. Таким образом, лемма 3.1 справедлива.
Из определения 1.2 непосредственно следует
Лемма 3.2. Пусть F Е T3(I ) удовлетворяет (А.2). Тогда косое произведение F имеет плотное множество периодических точек.
Далее покажем, что свойство топологической транзитивности влечёт за собой равномерную аппроксимируемость фазового пространства, периодическими орбитами динамической системы рассматриваемого класса. Для этого сначала убедимся в том, что топологическая транзитивность косого произведения из класса T3(I ) влечёт плотность множества его периодических точек.
Лемма 3.3. Пусть F Е T3(I ) удовлетворяет условию (А.1). Тогда для любого х Е Ii отображение gx(у) не имеет блуждающих интервалов.
Доказательство. В силу условия (С.2) и леммы 2.9 отображение gx (у) не имеет блуждающих интервалов при всех х Е Ii.
Лемма 3.4. Пусть F Е T3(I ) удовлетворяет условию (А.1). Тогда для любого х Е Ii отображение gx(у) не имеет аттракторов.
Доказательство. Допустим, существует точка х* Е Ii такая, что отображение gx* (у) имеет периодический аттрактор у* (наименьшего) периода п. В силу свойства (С.2), леммы 2.1 и леммы 2.2 gx*,2(cx*) = 02. Таким образ ом, ни точка сх*, ни один из её прообразов не принадлежат области притяжения периодического аттрактора у*.
Заметим, что точка у* имеет максимальную окрестность U, не содержащую саму точку сх* и всевозможные её прообразы (U не пусто, так как содержит область непосредственного притяжения точки у*). Тогда dU состоит из некоторых прообразов критической точки сх* — с/ и сг порядков I и г соответственно.
-
1) Пусть I = г = 1. Тогда точка сх* принадлежит множеству U. Последнее противоречит выбору интервала U .
-
2) Положим I = г > 2. Тогда точка сх* принадлежит интервалу ^^д*ф 1(сі), д1- 1(сг)). Следовательно, на интервале (сі,ст ) существует прообраз точки сх*. Последнее противоречит выбору интервала U.
-
3) Пусть теперь I = г. Для определённости будем считать, что I < г. Тогда справедливы следующие равенства:
дХ+ 1(сі ) = b2 и дХ* (с) = 02 при всех k > I + 2, дХ+ 1(сг) = Ь2 и дХ* (сг ) = 02 при всех s > г + 2.
Получаем, что дХ* 1([сі, сг ]) = [a2,b2] то есть множество U = [сі, сг ] содержит прообразы точки сх* . Последнее также противоречит выбору U. Таким образом, при всех ж Е І1 отображение дх(д) не имеет аттракторов. Лемма 3.4 доказана.
Тогда в силу предложения 2.8 всякое отображение дх,п при любом ж Е І1 и п > 1 топологически эквивалентно некоторой итерации логистического отображения вида дП : І2 ^ І2 при А = (ъ™2Д2! а значит, топологически транзитивно и обладает плотным множеством периодических точек. Последнее вместе с равенством Рег(! ) = І1 влечет за собой существование плотного множества периодических точек у рассматриваемого топологически транзитивного косого произведения.
Таким образом, доказано, что в рассматриваемом классе косых произведений условие (А.1) влечёт за, собой выполнение условия (В.1).
Лемма 3.5. Пусть Ғ Е Т3(І ) удовлетворяет условию (А.1). Тогда косое произведение Ғ удовлетвор.яст условию (А.2)
Доказательство. Как показано выше, множество периодических точек отображения Ғ плотно в прямоугольнике І. Возьмём произвольно и зафиксируем действительное число Ф > 0 и построим по нему разбиение Р прямоугольника І на т открытых подпрямоугольников Ji, 1 < г < т, с параметром разбиения А(Р) < Ф. Рассмотрим произвольную транзитивную точку (ж* , у*) отображения Ғ. Введём следующие обозначения:
п1 = min { k| Ғfc(ж*, у*) Е J1}, п2 = min {к|Ғ k(ж*,у*) Е J2 }, ..., пт = min {k|F k (ж* , у*) Е Jm} .
Положим по = max {пД. Обозначим через р метрику в І, например, согласованную с то-
Кг<т
пологией произведения в І. Тогда р(ҒПі(ж*, у*), dJi) — это расстояние между щ-й итерацией точки (ж*, у*) и границей прямоугольника Ji, пусть d' =mіп{р(Ғп*(ж*, у*),дJi), 1 < г < т} — минимальное из таких расстояний. Обозначим е = min {е', d'}. В силу равномерной непрерывности косого произведения Ғ по числу е укажем число 5 > 0 такое, что max р (Ғ п(ж* ,у*),Ғ п(ж,у)) <Ф V (ж,у) ЕU ((ж*, у*), 5),
О<п<по 2
где U ((ж*, у*), 5) — окрестность точки (ж*, у*) радііуса 5.
Тогда произвольная точка (жо,уо) Е Рег(Ғ )QU((ж*,у*),5) за первые по итераций попадёт во внутренность каждого из открытых подпрямоугольников разбиения Р, то есть орбита точки (жо,уо) аппроксимирует прямоугольник І с точностью до е. Лемма Зю дока-зяня.
Далее показано, что при добавлении условия (С.4) плотность периодических точек косого произведения из выделенного класса влечёт как топологическую транзитивность, так и равномерную аппроксимируемость фазового пространства, периодическими орбитами.
Лемма 3.6. Пусть Ғ Е Т'3(І ) удовлетворяет условиям (С.4) и (В.1). Тогда косое произведение Ғ удовлетворяет каэіедому из условий (А.1) и (А.2).
Доказательство. Пусть (жо, уо) — внутренняя периодическая точка отображения Ғ, удовлетворяющая условию (С.4). Тогда жо — внутренняя /-периодическая точка (обозначим через п её период), правостороннее и левостороннее неустойчивые многообразия которой равны всему отрезку Ii. Покажем, что какую бы периодическую точку (ж, у) € Рет (Ғ € Т3(I )) мы ни взяли, она удовлетворяет условию (С.4).
Предположим противное. Пусть существует (ж, у) € Рет(Ғ) такая, что ж € Рет(/) и имеет период к. Пусть для определённости ІП^ж,/к) = р. Тогда ІП^ж,/к) = J , где J — вполне инвариантный относительно /к интервал, отличный от Ii. Тогда J не содержит точку ж*. Пусть Orbf (J) = J|J/(J)U •••U/k-i(J) — вполне инвариантное относительно отображения / множество. Множество Orbf(J) не содержит точку ж*, следовательно, существует правосторонняя окрестность U + (ж*) такая, что U + (ж*) QOrbf(J) = 0. Кроме того, в силу условия (С.4) сущеетвует I € N такое, что /lnU + (ж*) = Ii. Значит, в U + (ж*) существует некоторый прообраз отрезка J. Обозначим его через J- С U + (ж*). Тогда существует по € N такое, что при любом п > по /п (J-) € Orbf (J). то есть J- — блуждающий отпосителыю / интервал (J_ состоит из блуждающих точек). Следовательно, в J- не существует периодических точек, что противоречит условию (В.1). Таким образом, в условиях теоремы В любая периодическая точка фактор-отображения / имеет правостороннее неустойчивое многообразие, совпадающее со всем отрезком Ii. Аналогичным образом это свойство доказывается и для левосторонних неустойчивых многообразий /-периодических точек.
Рассмотрим два произвольных открытых множества U, V С Ii. Тогда в U существует некая периодическая точка жо, обозначим её период через п. Возьмём произвольную правостороннюю окрестность U +(жо) С U. Тогда в силу условия (С.4) существует натуральное число s такое, что /sn (U + (жо)) = Ii D V. Последнее означает, что отображение / топологически транзитивно (см. критерий топологической транзитивности).
В силу условий (С.2), (С.3) и плотности множества периодических точек косого произведения отображение дх(у) при каждом ж € Ii является сюръективным унимодальным отображением, не обладающим ни аттракторами, ни блуждающими интервалами. Следовательно, дх(у) при каждом ж € Ii топологически эквивалентно некоторой итерации логистического отображения вида у = 4ж(1 - ж), т.е. дх(у) топологически транзитивно. Таким образом, периодические орбиты отображения дх(у) равномерно аппроксимируют отрезок I2 [16]. Последнее вместе с равіюмеріюй аппроксимируемостью отрезка. Ii периодическими орбитами / влечёт за собой равномерную аппроксимируемость прямоугольника I периодическими орбитами Ғ. Тогда в силу леммы 3.1 отображение Ғ топологически транзитивно. Лемма. 3.6 доказана.
Теоремы А и В доказаны.
Отметим, что дополнительное условие (С.4) опустить нельзя. Одно лишь свойство плотности множества периодических точек отображения Ғ рассматриваемого класса не влечет за. собой топологическую транзитивность.
Примером обладающего плотным множеством периодических точек, но не топологически транзитивного косого произведения из T3(I ) может служить отображение Ғ1(ж,у) : [0,1]2 ^ [0,1]2 с фактором
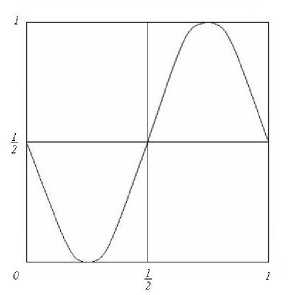
Рис. 1
/ (ж)=- у^3+1бж2 - 136ж+2
(см. рис. 1) и отображениями в слоях дх(у) при любых (ж, у) € I, определённые так, как это сделано для отображения Ғ (см. раздел 4). Тогда Рет(Ғ1) = [0,1]2. но Ғ1 не является топологически транзитивным, поскольку фактор-отображеіше / имеет два. ішварпаіиных промежутка. [0, 2) 11 ( 2, 1L
4. Пример косого произведения, имеющего аттрактор с непустой внутренностью
Докажем теорему существования косого произведения из класса 1'3(1 ).
Теорема 4.1. Существует топологически транзитивное косое произведение F G 1^1 ).
Доказательство. Определим косое произведение F : [0,1]2 ^ [0,1]2 в силу следующих равенств:
F(ж,у) = (4ж(1 — ж), дх(у)), (4)
где
у дх(у( = j
а(ж( (г — Ь(ж)) (г — с(ж)) (г — d(ж)') dz,
а(ж), Ь(ж), с(ж) и d(ж) — С 3-гладкие на отрезке [0,1] функции действительного переменного.
Равенство (5) может быть записано следующим образом:
дж(у( = оо(ж)у4 + щ(ж)у3 + О2(ж')у‘2 + О3(ж)у,
где оо(ж) = щщ;
Й1(ж) =
а(х)(Ь(х)+с(х)+(х)) .
3 :
02(ж) =
a^^b^d^+b^c^+c^d^x)) 2
оз(ж) = —o(ж)b(ж)с(ж)d(ж).
Найдём функции о(ж), Ь(ж), с(ж) и d(ж), исходя из следующих условий:
-
д.(1) = 0;
-
gx(tx( = 1;
Эд^ (у) I _ -|.
Эу |У=0 = 1;
Эд^^у)
Эу vy=tx = 0
где при каждом ж G [0,1] tx = ^ + отображения дх(у) по перемешюй у. Имеем
: [0,1] ^ [0.5, 0.6] — абсцисса критической точки
o(tx) =
-
4(t2 — 2t2 + 4tx — 2) '2 ( 'х — 1)2 ;
c(tx) =
2tX — t3 — 4t2 +11tx — 6 V 4t2 — 20t7 + 49t2 — 92tX + 162tX — 204t3 + 201t2 — 132tx + 36
St3 — 16t2 + 32tx — 16 + St3 — 16t2 + 32tx — 16
b(tx)
. 2t4 — t3 — 4t2 + 11Д — 6
c(t2) + 4(t 2 — 2- + 4t . — 2) ;
d(t2 ) ' x .
Отметим, что функции o(tx), b(tx ), c(tx ) и d(tx ) корректно определены при всех ж G [0,1].
На рис. 2 приведён график функции д2 (у) : [0,1]2 ^ [0,1]. На рис. 3 приведён график функции у = дх (у) при ж = 0.5.
В силу (4) фактор-отображение построенного косого произведения есть унимодальная С 3-гладкая сюръекция отрезка [0, 1]; функция д(ж, у) есть С 3-гладкая по совокупности переменных ж и у сюръекция квадрата [0, 1]2 на от резок [0, 1], причем при каждом ж G [0,1] отображение в слое дх(у( является унимодальной сюръекцией отрезка [0, 1] такой, что на [0, 1Хо + 2 ] д2 ( у ) гтрого воз растает по у. а на, (120 + 2, 1] дх (у) строго убывает по у. причём
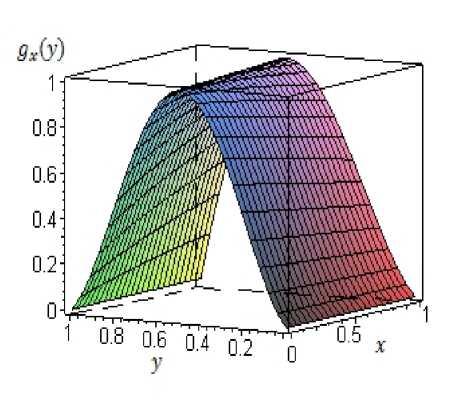
Рис. 2
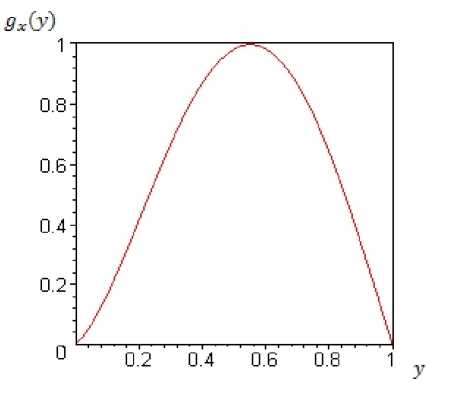
Рис. 3
при любом ж € [0, 1] справедливо дж(0) = дж (1) = 0 и дж(у) имеет неплоскую критическую точку tж = ^ + 2.
Покажем, что шварциан построенного косого произведения отрицателен. Для этого нам потребуется следующее утверждение.
Предложение 4.2. [12, гл. 4, §2] Если f(ж) — полином степени > 2 и все корни f‘(ж) = 0 действительны, то S f (ж) < 0 всюду, где f‘(ж) = 0.
Производная ^дуГ) = а(ж)(у — Ь(ж))(у — с(ж))(у — Дж)) имеет три действительных корня при каждом ж € [0,1]. Таким образом, в силу предложения 4.2 S (дж(у)) < 0.
Покажем, что построенное косое произведение топологически транзитивно.
Действительно, в силу своего задания дж,п(у) не имеет блуждающих интервалов (см. лемму 2.9) при всех ж € [0, 1] и п > 2. Кроме того, дж,п(у) не имеет периодических аттракторов, так как в этом случае в область притяжения периодического аттрактора попала бы критическая точка или один из её прообразов, что невозможно, так как дж,п(1) = 0 при всех ж € [0, 1] и п > 2. Тогда в силу предложения 2.8 дж,п(у) топологически сопряжено с п-й итерацией фактор-отображения f (ж) = 4ж(1 —ж) (см. предложение 2.8). и вместе с f (ж) отображение дж,п топологически транзитивно (см., например, [14, гл. 6, п. 6.1.1]).
Топологическая транзитивность f (ж) означает, что существует точка ж* € [0,1] такая, что ш(ж*, f) = [0, 1], (8)
где ш(ж*, f ) — ш- предельное множество /-траектории тонки ж*. Отображение f (ж) обладает также следующими свойствами:
-
1) f (ж) имеет периодические точки любого периода;
-
2) [0, 1] = Per(f) [14. гл. 6. п. 6.1.1]).
Из равенства (8) и свойства 2) следует возможность аппроксимации отрезка [0, 1] f- периодической орбитой с произвольной наперед заданной степенью точности [20], [16]. Последнее означает, что для любого е > 0 и произвольного разбиения Рж отрезка [0, 1] с параметром разбиения А(Рж) < е найдется f-периодическая орбита Of такая, что внутренность каждого отрезка разбиения Рж содержит хотя бы одну точку орбиты Of.
Возьмем произвольно и зафиксируем е € (0, 1). Построим разбиение Рж отрезка [0, 1] оси абсцисс на ([-] +1) равных отрезков. Тогда А(Рж) < е. Укажем f-периодическую орбиту Of (ж0) так, что внутри каждого отрезка разбиения Рж содержится хотя бы одна точка орбиты Of (ж0) (при этом точка ж0 принадлежит внутренности первого по порядку отрезка разбиения Рж). Обозначим через т(ж0) (наименьший) период периодической орбиты
Of (ж0) = {ж0, / (ж0),..., / т(х0)-1(ж0)}, где т(ж° ) > [ 1 ] + 1 (существование орбиты с таким периодом вытекает из свойства 1)).
Пусть е' = 2 Х(Рх). Построим разбиение Ру отрезка [0, 1] оси ординат на ([ 1 ] + 1) равных отрезков Jo Р J1 Р ... Р Jk-p где к = [ф] + 1, и JT Р Jr+1 в том и только том случае, если для любых различных ж' G Jr, ж'' G Jr+1 выполнено ж' < ж''. Имеем Х(Ру ) < е' < 2е.
Так как при всех 0 < г < т(ж0) — 1 отображение gj і (х0) (у) топологически транзитивно, то непрерывность Ғ вместе с равенством (2) влекут за собой топологическую транзитивность сужения Е^ (х0)х[0,1]- Пусть для определенности у0 - некоторая транзитивная точка отображения дхо (у). лежащая во внутренности отрезка, J0 разбиения Ру. Тогда траектория {Ғ г(ж0, у0)}г>0 всюду плотна во множестве Of (ж0) х [0, 1]. Обозначим через грТ, где 0 < j < т(ж0) — 1, 0 < г < к — 1, наименьшие неотрицательные значения дискретного времени г такие, что
Ғ^(ж0, у0) G {/j(ж0)} х гниг, здесь гntJr - внутренность отрезка JT. Так как множество указанных неотрицательных целых чисел конечно, то корректно определено натуральное число
г* = max {г^ Т }.
0<^<т(ж0)-1 ’
0 Отметим, что г* > кт(ж0). Используя равномерную непрерывность отображения дх,г* (у) в квадрате [0, 1]2. по нис.ту е' указкем 5 > 0 так. чтобы при всех у G [0, 1] таких, что |у — у0| < 5, выполнялось неравенство max фх0, г (у) — дж0,г(у0)| < е', (9) 0<г<г* каково бы ни было ж0 G Рег(/). Топологическая сопряженность отображений ухо (у) и ут(х ) (ж) позволяет указать точку у0 G Рег(дхо) так. что (наименьший) период т(у0) тотikii у0 отпоентс.тыю дхо удовлетворяет неравенству т(у0) > к (то есть период Ғ-перііодическоп тонки (ж0; у0) - равньш т(ж0)т(у0). не меньше, чем кт(ж0)); |у0 — у0| < 5, и в силу (9) верно max |дх0,г(у0) — дхо,г(у0)| < е. 0<г<г* Последнее вместе с выбором чисел е' и грг означает, что внутренность каждого из ([|] +1)2 квадратов, сторонами которых служат отрезки разбиений Рх и Р^, где разбиение Р^ получено делением отрезка [0, 1] оси ординат на ([1 ] + 1) равных частей, содержит хотя бы одну точку периодической орбиты Ор ((ж0; у0))- Таким образом, квадрат [0, 1]2 с произвольной, наперед заданной степенью точности можно аппроксимировать периодическими орбитами отображения Ғ. Отсюда в силу леммы 3.1 следует, что построенное косое произведение Ғ топологически транзитивно. Теорема. 4.1. доказана. Следствие 4.3. Косое произведение Ғ : [0,1]2 ^ [0,1]2, построенное в теореме 4.1 допускает свое естественное расширение Ғ* : [0,1] х [—0.25,1.05] ^ [0,1] х [—0.25,1.05]. На рис. 4 приведён график функции дх(у) : [0,1] х [—0.25,1.05] ^ [—0.25,1.05], на рис. 5 — график функции у = дх(у) при ж = 0.5. Введём понятие аттрактора, динамической системы. Определение 4.4 [6, ч. 1, гл. 3, § 3.3]. Компактное множество А С I называется аттрактором косого произведения Ғ : I ^ I, если существует такая окрестность U множества А II такое натуральное число п. что Ғп(и) С U и А = Q Ғ^(U). k>0 Теорема 4.5. Косое произведение Ғ* : [0,1] х [—0.25,1.05] ^ [0,1] х [—0.25,1.05], определённое равенствами (4), (5), имеет аттрактор А = [0,1]2. Доказательство. Для доказательства, данной теоремы воспользуемся определением 4.4. Возьмём U = [0,1] х [—0.25,1.05]. Из определения Ғ* следует, что при любом натуральном п ^(U) С U. Рис. 4 Рис. 5 Покажем, что А = Q F* (U). Действительно, для каждого ж € [0,1] поло жим Ах рав-к>0 ным наименьшему корню отображения дх на от резке [-0.25,1.05] (см. рис. 5). Тогда при любом ж € [0,1] имеем 1) дж([0,1]) С [0,1]; 2) дД[-0.25,Аж]) С [0,1]; 3) дх([1,1.05]) С [-0.25, Аж]; 4) отрезок [Аж, 0] под действием отображений в слоях стягивается к точке 0, так как точка 0 является притягиватотцей слева, неподвижпой точкой каждого отображения дх. 4.5 доказана. Таким образом, А = Q F*(U), а следовательно, множество А — аттрактор F*. Теорема к>0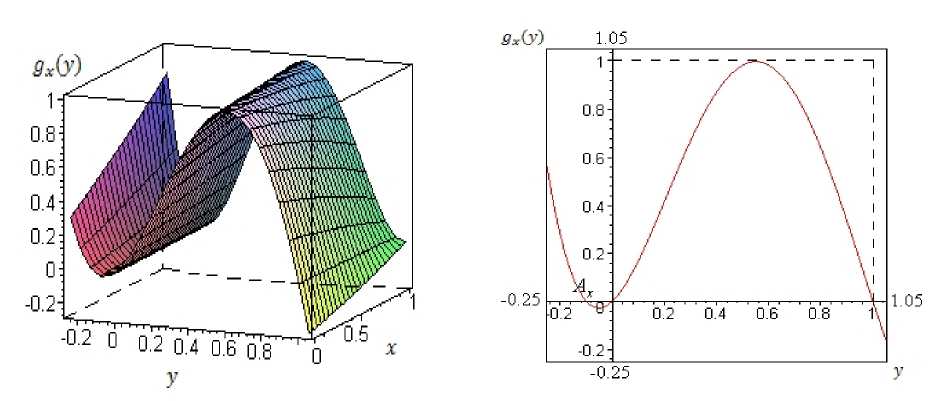
Список литературы Топологическая транзитивность косых произведений в плоскости с отрицательным шварцианом семейства отображений в слоях
- Биркгоф Д. Динамические системы. -Ижевск: Издат. дом «Удмуртский университет», 1999.
- Hedlund G.A. A class of transformations of the plane//Proc. Cambr. Phil. Soc. -1955. -V. 51, N 4. -P. 554-564.
- Аносов Д.В. Об аддитивном функциональном гомологическом уравнении, связанном с эргодическим поворотом окружности//Изв. АН СССР. Сер. матем. -1973. -Т. 37, Ч. 6. -С. 1259-1274.
- Diaz L.J., Pujals E., Uras R. Partial hyperbolicity and robast transitivity//Acta Mathematica. -1999. -V. 183. -P. 1-43.
- Городецкий А.С., Ильяшенко Ю.С. Некоторые свойства косых произведений над подковой и соленоидом//Труды матем. ин-та им. В.А. Стеклова. -2000. -Т. 231. -С. 96-118.
- Каток А., Хасселблат Б. Введение в современную теорию динамических систем. -М.: Факториал, 1999.
- Сидоров Е.А. Топологически транзитивные цилиндрические каскады//Математические заметки. -1973. -Т. 14. -Ч. 3.
- Alseda Ll., Kolyada S., Llibre J., Snoha L. Entropy and Periodic Points for Transitive Maps//Trans. Amer. Math. Soc. -1999. -V. 351. -P. 1551-1575.
- Ефремова Л.С., Фильченков А.С. О простейших топологически транзитивных косых произведениях в плоскости//Труды международной конференции по дифференциальным уравнениям и динамическим системам. -Суздаль, 2008.
- Ефремова Л.С., Фильченков А.С. Об одном примере топологически транзитивного косого произведения в плоскости//Проблемы фундаментальной и прикладной математики. -М.: МФТИ, 2009. -С. 61-68.
- Bamon R., Kiwi J., Rivera-Letelier J., Urzua R. On the Topology of Solenoidal attractors of the Cylinder//Annales de l'Institut Henri Poincare (C) Non Linear Analysis. -March-April 2006. -V. 23, I. 2. -P. 209-236.
- Шарковский А.Н., Майстренко Ю.Л., Романенко Е.Ю. Разностные уравнения и их приложения. -Киев: Наукова думка, 1986.
- Шарковський О.М. Неблукаючi точки та центр неперевного вiдображения прямоi в себе//Доп. АН УРСР. -1964. -Т. 7. -С. 865-868.
- Брур Х.В., Дюмортье Ф., ван Стрин С., Tакенс Ф. Структуры в динамике. -М.-Ижевск, 2003.
- Melo W. de, S. Strien van. One-Dimensional Dynamics. -Berlin: Springer, 1996.
- D'Aniello E., Steele T. Approximating 𝜔-limit sets with periodic orbits//Aequationes Math. -2008. -V. 75. -P. 93-102.
- Куратовский Л. Tопология. -М.: Мир. -T. 1. 1966; Т. 2. 1969.
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. -М.: Наука, 1972.
- Мартин Н., Ингленд Дж. Математическая теория энтропии/пер. с англ. -М.: Мир, 1988.
- Шарковский А.Н. О притягивающих и притягивающихся множествах//ДАН СССР. -1966. -Т. 170, Ч. 6. -С. 1276-1278.


