Топологический заряд оптических вихрей без радиальной симметрии

Лазерные вихревые пучки [1], или оптические вихри (ОВ), интенсивно исследуются в настоящее время, так как применяются при решении многих задач оптики. ОВ применяются в квантовой информатике [2] и криптографии [3], системах беспроводной связи [4], при передаче информации по волокну [5], при генерации второй гармоники [6], в интерферометрии коротких импульсов [7], при зондировании сред с турбулентностью [8]. Вихревые пучки характеризуются двумя основными параметрами: топологическим зарядом (ТЗ) [9] и орбитальным угловым моментом (ОУМ) [10]. Обе эти характеристики описывают разные стороны ОВ: ТЗ зависит только от фазы светового поля, а ОУМ зависит как от фазы, так и от амплитуды (интенсивности). Измерять ТЗ можно с помощью цилиндрической линзы [11] или треугольной диафрагмы [12]. ОУМ можно измерять также с помощью цилиндрической линзы [13, 14]. ОУМ-спектр оптических вихрей, то есть энергетический вклад в каждую угловую гармонику, содержащуюся в лазерном пучке, можно измерять с помощью многопорядкового дифракционного оптического элемента [15] или с помощью моментов интенсивности [16, 17]. Для ОВ с радиальной симметрией (например, пучки Лагерра – Гаусса (ЛГ) [18], Бесселя – Гаусса (БГ) [19]), комплексную амплитуду которых можно представить в виде E ( r , ϕ , z )= A ( r , z ) exp( in ϕ ), где

A ( r , z ) – радиальная составляющая комплексной амплитуды пучка, n – топологический заряд пучка, ( r , ϕ , z ) – цилиндрические координаты, ТЗ равен нормированному на мощность пучка ОУМ и равен n . Причём для радиальных ОВ с целым ТЗ он сохраняется при распространении пучка в пространстве. Для других вихревых пучков ТЗ нужно вычислять отдельно. Если ОУМ пучка сохраняется при распространении и его можно вычислять в начальной плоскости, то ТЗ не всегда сохраняется. Например, ТЗ комбинированного пучка, состоящего из двух мод Лагерра – Гаусса с разными радиусами перетяжки Гауссова пучка, не сохраняется [20].

В этой работе мы найдём ТЗ некоторых вихревых лазерных пучков, не обладающих радиальной симметрией. Эти пучки были ранее рассмотрены авторами, и для них были найдены нормированные ОУМ, но ТЗ этих пучков не рассматривался. Мы найдём ТЗ для асимметричного пучка Лагерра – Гаусса [21], асимметричного пучка Бесселя – Гаусса [22], асимметричного пучка Куммера [23], суммы двух мод Эрмита – Гаусса [24] и вихревого пучка Эрмита – Гаусса [25].

В [26] мы уже рассматривали ТЗ некоторых видов оптических вихрей без круговой симметрии. Асимметрия появлялась в результате ограничения асимметричной диафрагмой, поперечного смещения оптического вихря, соосной интерференции оптического вихря с другими осевыми вихрями или с Гауссовым пучком, или растяжения винтовой фазы по одной декартовой координате. В данной работе мы рассматриваем ТЗ пучков, асимметрия которых вызвана либо поперечным смещением их комплексной амплитуды на мнимое расстояние, либо суперпозицией невихревых пучков Эрмита – Гаусса.

Нормированный на мощность ОУМ аЛГ-пучка имеет вид [21]:

J z W

1. Топологический заряд асимметричного пучка Лагерра – Гаусса

При распространении в свободном пространстве на произвольном расстоянии z комплексная амплитуда асимметричного пучка ЛГ (аЛГ-пучка) [21] имеет вид:

E ( x, y, z ) =

w ( 0 ) ^{w ( z} )

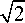
^{w ( z} )

x[ ( x - x 0 ) + i ( y - y 0 ) ] n L nm

x exp

где

-

P ² + ik P ² w ² ( z ) 2 R ( z )

2 p ² w ^{2 (} z )

- i ( n + 2 m + 1 ) Z ( z )

p ² = ( x - x 0 ) ² + ( y - y 0 ) ²,

,, I ^z I

1 ⁺ l — I ,

I z r )

z ( z ) = arctg I     I ,

V ^zR /

где ( x , y , z ) и ( r , ф , z ) - декартовы и цилиндрические координаты, ( x 0 , y 0 ) – комплексные координаты смещения центра пучка ЛГ, w – радиус перетяжки Гауссова пучка, n – ТЗ оптического вихря, L ⁿm ( x ) – присоединённый многочлен Лагерра, z R = kw ²/2 – расстояние Рэлея, к 2 п / Х - волновое число света с длиной волны X . В поперечном сечении интенсивность такого пучка не имеет радиальной симметрии, как у обычных пучков ЛГ [18]. Если ( x 0 , y 0 ) – действительные числа, то пучок (1) становится обычной модой ЛГ, смещённой с оптической оси.

В дальнейшем мы будем сравнивать полученные в этой работе ТЗ различных ОВ с их ОУМ, которые были получены ранее. Для этого приведём здесь выражения, по которым рассчитывается ОУМ параксиальных лазерных пучков и мощность пучка [21]:

т Г 5E 5E Lm

Jz = Im E I x--y— | dx dy,(3)

^ V dy

W = JJ E * E dx dy.(4)

B ²

2Im ( x 0 y 0 )

w ²

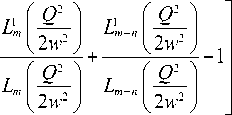
, (5)

где Q = 2 i ^( Im x 0 ) ² + ( Im y 0 ) ².

Увеличение или уменьшение нормированного ОУМ по сравнению с величиной ТЗ n полностью определяется знаком величины Im( x 0 ^* y 0 ) , так как выражение в квадратных скобках (5) всегда больше или равно 1. Рассчитаем ТЗ аЛГ-пучка (1) по формуле Берри [9]:

1 2Л      Д

TC = lim— [ dф—arg E ( r , ф ) = r -» 2 n 0     дф ^{V 7}

1 г т ²!a д E ( r , ф ) / дф

= limIm d ф .

2 n r ^” ^J₀       E ( r , ф )

Выберем комплексное смещение в (2) в виде x 0 = aw , y 0 = iaw , тогда множитель в (1) [( x – x 0 )+ i ( y – y 0 )] ⁿ будет иметь простой вид rⁿe ^{in φ}, а переменная ρ² в (2) будет иметь следующий вид: p ² = ( x - x n )² + ( y - y n )² = r ²-2 awre ^ф , где a – безразмерная константа, от величины которой зависит асимметрия пучка. С учётом этих замечаний производная по углу ф от функции (1) будет иметь вид:

д E ( r , ф , z ) дф

= inE ( r , ф , z ) -

ik

w ² ( z ) 2 R ( z )

( 2 iawre i ^ф ) E ( r , ф , z )

4 iawre i ^ф 1 d \          \

^2( z T L ^ d ^ ^{m (}^ ^{( r} , ^ф , ^z ),

где

2 p ²

^{w 2 ( z} ) .

Подставим (8) в (7), получим:

TC = — x 2 n

2Л        I x lim Im [ dф < in -r ^rc

0 I

ik

w ² ( z ) 2 R ( z )

i4awre‘ф 1 дLm (^) _/ ---E (r, ф, z w2(z) Lnm (^) д^ '

= n + lim Re r ^rc

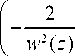
ik I 2 ^л ---- raw [ dф e

R ( z ) J     ^J

2n

- lim Re [ d ф r ^rc      J

2 rnawe i ^ф r ( r - 2 awe i ^ф )

= n .

( 2 iarwe i ^ф ) -

-

При получении третьего слагаемого в (9) при переходе к пределу r → ∞ воспользовались асимптотикой для присоединенных многочленов Лагерра [ L m ( x )] ^{- 1} д L ⁿm ( x )/ д x ® n / x (так как число нулей у многочлена конечно, мы выбираем радиус окружности r , за которой полином не обращается в нуль). Третье слагаемое в (9) при переходе к пределу r → ∞ равно нулю, так как в знаменателе вторая степень, а в числителе первая степень радиальной переменной r . Второе слагаемое в (9) тоже равно нулю, но по другой причине. Хотя в числителе во втором слагаемом в качестве сомножителя присутствует радиальная переменная r , которая стремится к бесконечности, но в числителе также есть интеграл по углу ф от экспоненты exp( i ф ) от 0 до 2 п , который равен нулю. Таким образом, из (9) следует, что ТЗ асимметричной моды ЛГ будет равен n . То есть комплексное смещение координат для обычной моды ЛГ приводит к изменению её формы (1), изменению её ОУМ (5), но не изменяет её ТЗ (9). Заметим также, что ТЗ аЛГ-пучка (1), равный n , сохраняется при распространении, так как расчёт (9) был сделан при любом z .

2. Топологический заряд асимметричного пучка Бесселя–Гаусса

В (12) с – это безразмерная постоянная, от которой зависит асимметрия аБГ-пучка. Пучок аБГ (12), в отличие от аЛГ-пучка (1), получен не с помощью комплексного смещения координат, а с помощью суперпозиции обычных бесселевых пучков, которая математически выражается с помощью справочного ряда [22]:

Z — J k _+v ( x ) = x ^{v /2} ( x - 2 1 ) ^{-v /2} J v (V x ² - 2 tx ) . (13) k =0 ^k ! '

Можно получить выражение для ОУМ для аБГ-пучка, нормированного на мощность [22]:

Jz = n + у c ² p PI n + P ⁽ У )

W “    ( P ! ) ²

да z p =0

c ^{2 P} I n + p ( У )

⁽ P ^{! ) 2}

-1

, (14)

Запишем комплексную амплитуду пучка Бесселя– Гаусса (БГ-пучки) [19] в начальной плоскости z =0:

( r ²        I

E_n ( r , ф , z = 0 ) = exp I--+ in ф I J_n ( a r ) ,

I ® 0       J

где a = k sin 9 0 = (2 n / X )sin 9 0 - масштабирующий множитель, k= 2 п / X - волновое число света с длиной волны X , 9 0 - угол конической волны, формирующей пучок Бесселя. В любой другой плоскости z комплексная амплитуда (10) будет иметь вид:

где y = a ² ® 0/4. Выражение (14) дальше упростить не удаётся. Из (14) следует, что ОУМ аБГ-пучков больше n , так как все слагаемые рядов в (14) положительные. То есть с ростом параметра с растёт асимметрия аБГ-пучка и почти линейно растёт его ОУМ. Из четырёх возможных причин увеличения ОУМ (рост топологического заряда, смещение центра тяжести, астигматизм и анизотропия среды) в данном случае ОУМ возрастает из-за смещения центра тяжести, так как, согласно (12), оптический вихрь остаётся на оптической оси, а согласно (13) с ростом асимметрии больший вклад начинают давать моды Бесселя высших порядков, у которых главное кольцо интенсивности имеет больший радиус, что приводит к удалению центра тяжести пучка от оптической оси. Найдём ТЗ аБГ-пучка (12) по формуле (7). Но сначала выпишем производную от функции (12) по азимутальному углу (пусть J n ( x ) ≠ 0, чтобы не делить на ноль):

„ ,         .         , / x I ,         i a² z I

E n ( r , ф , z ) = q ^{- 1} ( z ) exp I ikz - I x (      2 kq ( z ) J

д E n ( r , ф , z ; c )

---------------- = inE n ( r , ф , z ; c ) + дф

I r2          • I r x exp I--—— + inф I Jn

( ® 0 q ( z )       J

incq ( z ) e* ^ф a r - 2 cq ( z ) ei^

E n ( r , ф , z ; c ) -

a r

q ⁽ z ) J ,

где q ( z ) = 1 + iz / z 0 , z ₀ = k ® 0/2 — длина Рэлея, Ю о - радиус перетяжки Гауссова пучка, J n ( x ) – функция Бесселя первого рода n -го порядка. Комплексная амплитуда асимметричного пучка Бесселя – Гаусса (аБГ-пучок) имеет вид [22]:

E n ( r , ф , z ; c )

1 q ( z )

a r ar - 2cq(z)exp(i ф)

n 2

ic ( a r ) 1 ^/2 e i ^ф

1/2

[a r - 2 cq ( z ) e i ^ф J

,    д J „ ( x )

J - 1 ( x ) —(-^ д x

где x = q 1 ( z ){ a r [ a r -2 cq ( z )exp( i ф )]}^1/2. Тогда (7) примет вид:

Tv- 1 г _n 2^Пд J ,    ncq ( z ) ei ^ф

TC = — lim Re J d ф< n +-----—

^{2 n} r ^ да о [   a r - 2 cq ( z ) ei ^ф

c ( a r ) ^1/2 ei ^ф        1 S Jn ⁽ x ) _

I ,       ia2z         r2              | x exp I ikz-----+ inф Ix

(     2kq(z) q(z )®2      J x Jn {q-1 (z)^ar [ar - 2cq(z) exp (iф)

1^{/2 J}n ^{( x} ) ^{д x}

= n + lim Re r ^да

cJ ¹ (a r)         2n

Jn ( a r ) J d ф ei ^ф

^{2 n}            0

= n .

В (16) второе слагаемое под интегралом стремится к нулю при r → ∞, так как в знаменателе стоит первая степень радиальной переменной r . Третье слагаемое преобразуется в слагаемое, которое также равно нулю, но по другой причине. В третьем слагаемом в (16) присутствует отношение производной от функции Бесселя к самой функции Бесселя (функции Бесселя вынесены из интеграла, потому что при больших значениях r верно неравенство | а r | >> | 2cq ( z )|, и потому слагаемым 2 cq ( z ) e^{i φ} в аргументе функции Бесселя мы пренебрегли). При r → ∞ это отношение может быть любым числом, так как асимптотики функции Бесселя и её производной при большом аргументе имеют вид:

J n ( x >>  1)

»

n п

п

Производная от функции (19) по углу φ имеет вид:

d E . _ /           irawe* ^ф _ 2 irae* ^ф _

— = inE - ( m - n + i y )------ E +-- E .

дф                     s ² w

Подставим (20) в (7), получим:

TC = — х 2 п

2п '

х limIm Г d ’ in r ^^    j

0 V

ar

п w

i ( m - n + i y) rawe¹ ’ 2 irae i ^ф

( r - 2 awe ^ф )

2п j cos ф dф = n.

w

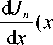
>> 1)

x

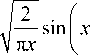
n п

п

а их отношение является тангенсом. Но также в третьем слагаемом в (16) присутствует интеграл по углу ф от экспоненты exp( i ф ) от 0 до 2 п , который равен нулю. Поэтому и все третье слагаемое в (16) будет равно нулю. Из (16) следует, что при любой степени асимметрии (при любом c ) и на любом расстоянии от начальной плоскости (при любом z ) у аБГ-пучка ТЗ будет равен n . Хотя ОУМ такого пучка будет увеличиваться с ростом степени асимметрии (14).

3. Топологический заряд асимметричного пучка Куммера

В [23] рассмотрены асимметричные пучки Куммера (аК-пучки), являющиеся точными решениями параксиального уравнения Гельмгольца. Комплексная амплитуда аК-пучка получается путём смещения в комплексную плоскость координат ( x → x – aw , y → y – iaw , где a – безразмерная действительная величина) обычного гипергеометрического пучка (или обычного пучка Куммера) [23] при любом z :

Из трёх слагаемых под интегралом в (21) первое равно n , второе слагаемое после перехода к пределу r → ∞ равно нулю, так как в знаменателе стоит квадрат, а в числителе первая степень радиальной переменной r . Третье слагаемое тоже равно нулю, так как интеграл по углу на периоде от косинуса равен точно нулю, хотя и умножается этот интеграл на величину, стремящуюся к бесконечности ( r → ∞). Таким образом, ТЗ асимметричного пучка Куммера в начальной плоскости равен n . С помощью (18) аналогично можно показать, что ТЗ (18) при любом z будет равен n .

4. Топологический заряд оптического вихря в виде суммы двух мод Эрмита – Гаусса

В [24] было показано, что при сложении двух пучков Эрмита–Гаусса (ЭГ) с номерами ( n , n + 1) и ( n + 1, n ) и с фазовым сдвигом на п /2 формируется оптический вихрь с орбитальным угловым моментом, пропорциональным номеру ( n + 1). В этом параграфе мы найдём топологический заряд такого ОВ. Пусть комплексная амплитуда композиции двух пучков ЭГ в начальной плоскости ( z =0) имеет вид:

w ²

E ( x , y ,0 ) = exp —2"" ( x ² + У 2 )

х

E s ( r , ф , z ) =

( - i ) ^{n + 1} 1 z 0

I m + n + 2 + iy хГ1-------------

V zq(z \ kwr

q -< m + i _у ^)/2( z ) _х

I ,          Iks I х exp inф +--i F

V         2 z J

I ⁿ

■ х

х[Hn (wx)Hn+1 (wy) + iYHn+1 (wx)Hn (wy)], где w = V2/w0, wо - радиус перетяжки Гауссова пучка. Постоянную Y положим равной единице. Для светового поля (22) можно получить нормированный ОУМ для любого целого n [24]:

m + n + 2 + i у

, n + 1, -^ I ,

где s ² = r ( r -2 awe ^ф), ^ = [ kws / (2 z^q ( z ))]², а i F i ( a , b , z ) -функция Куммера (вырожденная гипергеометрическая функция). В начальной плоскости ( z =0) комплексная амплитуда (18) смещённого пучка Куммера принимает вид:

E s ( r , ф , z = 0 ) =

rneinф I s Im-n+iY

---- — exp--

III wn ^ w J^

= - ( n + 1 ) .

W

Заметим, что из-за того, что сумма номеров обеих мод в (22) одинакова, то линейная комбинация (22) будет являться модой (фазы Гоу ( m + n + 1) arctg( z / z 0 ) у обеих мод тоже одинаковые) и при распространении будет сохранять свой вид, меняясь только масштабно.

Прежде чем вычислять ТЗ по формуле (7), ответ можно предсказать сразу. Действительно, первое слагаемое в (22) имеет n вертикальных линий нулей и

( n + 1) горизонтальных линий нулей. А второе слагаемое в (22), наоборот, имеет ( n + 1) вертикальных линий нулей (которые не совпадают с вертикальными линиями нулей первого слагаемого) и n горизонтальных линий нулей. Поэтому амплитуда (22) будет равна нулю в точках пересечения горизонтальных и вертикальных линий. Точек пересечения с амплитудой вблизи нуля x+iy будет n ², а точек пересечения с амплитудой вблизи нуля y+ix будет ( n + 1)². Поэтому ТЗ поля (22) будет равен TC = n ²–( n + 1)²=–(2 n + 1).

Для определения ТЗ пучка по его комплексной амплитуде (22) представим моды ЭГ в (22) через моды ЛГ (выражение (3.11) в [27]):

мод две (при k =0), поэтому ТЗ такой суперпозиции равен либо 2( n + 1), либо – 2( n + 1), в зависимости от того, у какой моды больше весовой коэффициент. Для полиномов Якоби известно свойство:

P_k ⁽“-^₽) (— z ) = (— 1 ) k P f^a)( z ) .                        (28)

Поэтому P ₀ ^{( n} , ^{n + 1)} (0) = P 0-^{n + 1, n} ) (0) и весовой коэффициент A — при моде ЛГ порядка 2( n + 1) равен нулю. Следовательно,

TC = — ( 2 n + 1 ) .

[ ( n + mу 2]

imHn (^)Hm (n) = E '(-2) k!Pn—k’m—k)(°)x k=0

x[ ( ^ + i n ) n ⁺ m -2 k + ( - 1 ) m ( ^ — i n ) n ⁺ m -2 ^k ]x           (24)

5. Топологический заряд вихревого пучка Эрмита – Гаусса

X Lp- + m — 2 k

( ^ 2 +n ² ) ,

В [25] показано, что если сложить не две моды ЭГ, а несколько, используя справочное выражение из [27]

где P – многочлены Якоби, а штрих у знака суммы означает, что при чётных n и m последнее слагаемое надо разделить пополам.

Произведения полиномов Эрмита из (22) тогда имеют вид:

nk

E      HlHk (x)Hn—к (У) = k=0 k!(n — k)!

= ( 1 + 1 ² ) n /2 H n

tx + y 1 + tP

H n ( wx ) H n + 1 ( wy ) =

n

= i — - — ¹ E ( — 2 ) k k ! P k n - k , n k ) ( 0 ) x k = 0

x w ^{2 n + 1 — 2 k}L kn ^{+ 1 — 2 k} ( w ² x ² + w ² y ² ) x

то можно получить вихревой пучок Эрмита – Гаусса, комплексная амплитуда которого имеет вид:

\         ( x ² + y ² I

U_n ( x , y , z ) = i n exp I--2— I x

/      . x 2n+1-2k    / i\n+1 /      . 2Пn+1-2k x (x + iy)       +(—1)   (x — iy)

n2n 2 и I iax + у I ^{x( 1 —} a ²) H n ljr^l.

IV1 — a ² )

H n + 1 ( wx ) H n ( wy ) =

= i—n £ (—2) kk! Pk

x w^{2n+1 2k}Lkn^{+1 2k} (w²x²+ w²y²)x

[/      . x2n+1—2k    / n\n /      . 2nn+1—2k 1

(x + iy)        +(—1) (x — iy)       ] .

Используя эти выражения, перепишем (22) в по-

Так как в (30) сумма номеров ЭГ-мод постоянная k +(n – k)= n = const, то все ЭГ-моды в линейной комбинации (30) имеют одинаковую фазовую скорость (одинаковые фазы Гоу (n + m + 1) arctg(z / z0)), и поэтому весь пучок (31) тоже является параксиальной модой и распространяется без изменения поперечной структуры интенсивности (с точностью до масштаба и вращения). Орбитальный угловой момент пучка (31) выражается формулой [25]:

лярных координатах:

E (r, ф,0) = (— i) n+1exp I — w2 r 2 |

----- x

2 J

xE(—2)k k!(wr)2n^+1—2k Lk^n+1—2k (w²r²)x       (27)

k=0

xF Ak e (2n+1—2k)ф — (—1)n Ake—i (2n+1—2kИ, где A± = Pk(n—k,n+1—k) (0) ± Pk(n+1—k,n—k) (0).

Получилась суперпозиция конечного числа мод ЛГ. Согласно [26], ТЗ такой суперпозиции равен ТЗ моды наивысшего (по модулю) порядка. В (29) таких

Jz     2an

.

I     1 + a²

Постоянный параметр a в (31) и (32) можно связать с углом поворота а цилиндрической линзы, которая преобразует пучок Эрмита – Гаусса с номером (0, n) в вихревой пучок ЭГ (31):

a1

cos а = ,       , sin а = ,      .                (33)

V1 + a²           V1 + a²

Найдем ТЗ вихревого пучка ЭГ (31). Для этого подставим выражение (31) в формулу (7), получим:

1            2π

TC = limIm dϕ r→∞ π0

∂E(r,ϕ)/∂ϕ E(r, ϕ)

n       2^πHn_-1(ircosϕcosα+rsinϕsinα)(-irsinϕcosα+rcosϕsinα)

= limIm dϕ

2π r^→∞   0                  Hn(ircosϕcosα+rsinϕsinα)

Перейдём к пределу r → ∞ в (34) и заменим многочлены Эрмита на одночлены с максимальной степенью Hn (x >> 1) ≈ (2x) ⁿ. Тогда вместо (34) получим:

1    2^π   n(-isinϕcosα+cosϕsinα

TC =Im dϕ

2π0     (icosϕcosα+sinϕsinα)

2π

=^-n dϕ       ^tgα       =-n.

2π0    cos2ϕ +tg2αsin2ϕ

При получении (35) воспользовались справочным интегралом [27]:

2^π       dϕ₌2π

0 cos2ϕ+γ2sin2ϕ γ

Сравнивая выражения для ОУМ (30) и ТЗ (33) для вихревого пучка ЭГ, видно, что ТЗ пучка не зависит от параметра a или от угла наклона α цилиндриче- ской линзы (33), а ОУМ зависит от этого параметра. Поэтому обе характеристики вихревых пучков (ОУМ и ТЗ) одинаково важны для их описания.

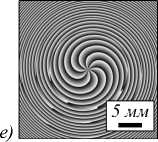
6.    Моделирование

На рис. 1 показаны распределения интенсивности и фазы асимметричного пучка Бесселя – Гаусса в трёх поперечных плоскостях: z =0 (в начальной плоскости) (рис. 1а, б), z = z0 (на расстоянии Рэлея) (рис. 1в, г) и z = 10z0 (в дальней зоне) (рис. 1д, е). Видно, что в начальной плоскости, кроме оптического вихря 8-го порядка, имеется множество оптических вихрей 1-го порядка. На расстоянии Рэлея такой вихрь всего один (в нижней левой части рис. 1г). В дальней зоне остаётся только центральный вихрь 8-го порядка. Поэтому при расчёте ТЗ были получены значения 11,9926 (при z =0), 8,8837 (при z = z0) и 7,9393 (при z = 10z0).

б)

е)

Рис. 1. Распределения интенсивности (а, в, д) и фазы (б, г, е) аБГ-пучка в трёх разных плоскостях. Параметры расчёта: длина волны λ=532 нм, радиус перетяжки w0=0,5 мм, порядок оптического вихря n = 8, масштабный множитель α=1/ w0, параметр асимметрии c=w0 /40, расстояние распространения z = 0 (начальная плоскость) (а, б), z = z0 (на расстоянии Рэлея) (в, г), и z =10z0 (в дальней зоне) (д, е), расчётная область – R ≤ x,y ≤ R, где R =10 мм (z =0), R =10 мм (z = z0), R=20 мм (z =10z0), число отсчётов – 2048×2048. ТЗ рассчитывался вдоль окружности x²+y²=R1², где R1=0,8R.

Полученные значения равны 11,9926 (а, б), 8,8837 (в, г) и 7,9393 (д, е)

Аналогично на рис. 2 показаны распределения интенсивности и фазы асимметричного пучка Лагерра– Гаусса в трёх поперечных плоскостях: z =0 (в начальной плоскости) (рис. 2а, б), z = z0 (на расстоянии Рэлея) (рис. 2в, г) и z = 10z0 (в дальней зоне) (рис. 2д, е). Видно, что в начальной плоскости, кроме оптического вихря 8-го порядка, имеется несколько оптических вихрей первого порядка. На расстоянии Рэлея таких вихрей несколько (отчётливо видны три вихря слева от центра рис. 1г). В дальней зоне остаётся только центральный вихрь 8-го порядка. При расчёте ТЗ были получены значения 7,9974 (при z =0), 7,9925 (при z = z0) и 7,9226 (при z = 10z0).

а)

в)

1 MM

Рис. 2. Распределения интенсивности (а, в, д) и фазы (б, г, е) аЛГ-пучка в трёх разных плоскостях. Параметры расчёта: длина волны λ=532 нм, радиус перетяжки w0=0,5 мм, порядок оптического вихря n = 8, радиальный индекс моды m =3, вектор смещения (x0, y0)=(0, iw0/4), расстояние распространения z = 0 (начальная плоскость) (а, б), z=z0 (на расстоянии Рэлея) (в, г), и z =10z0 (дальная зона) (д, е), расчётная область – R ≤ x,y ≤ R, где R =5 мм (z=0), R=5 мм (z = z0), R=30 мм (z =10z0), число отсчётов – 2048×2048. ТЗ рассчитывался по окружности x²+ y²=R1², где R1= 0,8R.

Полученные значения равны 7,9974 (а, б), 7,9925 (в, г) и 7,9226 (д, е)

На рис. 3 показаны распределения интенсивности и фазы асимметричного пучка Куммера в трёх поперечных плоскостях: z =0 (в начальной плоскости) (рис. 3а, б), z = z0 (на расстоянии Рэлея) (рис. 3в, г) и z = 10z0 (в дальней зоне) (рис. 3д, е). Видно, что, не- смотря на асимметричное распределение интенсивности, во всех плоскостях в центре имеется оптический вихрь первого порядка. При расчёте ТЗ были получены значения 0,9981 (при z =0), 0,9992 (при z = z0) и 0,9999 (при z = 10z0).

а)

д)

е)

Рис. 3. Распределения интенсивности (а, в, д) и фазы (б, г, е) асимметричного пучка Куммера в трёх разных плоскостях. Параметры расчёта: длина волны λ=532 нм, радиус перетяжки Гауссова пучка w0=0,5 мм, порядок оптического вихря n=1, параметры m и γ равны m =3 и γ =0, параметр смещения a = 0,2, расстояние распространения z = 0

(в начальной плоскости) (а, б), z=z0 (на расстоянии Рэлея) (в, г), и z =10z0 (в дальней зоне) (д, е), расчётная область –

R ≤ x,y ≤ R, где R =5 мм (z = 0), R =5 мм (z = z0), R =10 мм (z =10z0), число отсчётов на каждом рисунке – 2048 × 2048.

Вставка на рис. 3б показывает увеличенный фрагмент в центре. ТЗ вычислялся на окружности x²+y²=R1², где R1=0,8R.

Полученные значения равны 0,9981 (а, б), 0,9992 (в, г) и 0,9999 (д, е)

На рис. 4 показаны распределения интенсивности и фазы суммы двух мод Эрмита – Гаусса в начальной плоскости. Видно, что, несмотря на большое количество изолированных нулей, почти все они компенсируют друг друга (вихри первого и минус первого порядка) и на бесконечности остаётся лишь небольшое число скачков фазы. Это следует из того, что при обходе по контуру вблизи края рис. 4в (против часовой стрелки) имеется ровно 11 скачков фазы на –2π (по- казаны стрелками). При расчёте ТЗ было получено значение –10,9550, что соответствует теоретическому значению –(2n + 1).

На рис. 5 показаны распределения интенсивности и фазы вихревой моды Эрмита – Гаусса в начальной плоскости. Видно, что на вертикальной оси расположено 10 изолированных нулей интенсивности минус первого порядка, которые в сумме дают ТЗ, равный –10. При расчёте ТЗ было получено значение –9,9993.

а)

Рис. 5. Распределения интенсивности (а) и фазы (б) вихревой моды Эрмита – Гаусса в начальной плоскости. Параметры расчёта: длина волны λ=532 нм, радиус перетяжки Гауссова пучка w0= 0,5 мм, порядок оптического вихря n =10, параметр асимметрии a = 0,3, расчётная область –R ≤ x,y ≤ R, где R=5 мм, число отсчётов – 2048×2048. ТЗ вычислялся на окружности x²+ y²=R1², где R1=0,8R.

Полученное значение равно –9,9993

Рис. 4. Распределения интенсивности (а) и фазы (б) суммы двух мод Эрмита – Гаусса в начальной плоскости, а также увеличенный фрагмент (в) фазы в пунктирном квадрате на рис. 4б. Параметры расчёта: длина волны λ=532 нм, радиус перетяжки Гауссова пучка w0= 0,5 мм, порядок оптического вихря n =5, расчётная область – R ≤ x,y ≤ R, где R=5 мм, число отсчётов – 2048×2048.

Стрелками (в) показаны 11 скачков фазы на – 2π при обходе вдоль пунктирной окружности против часовой стрелки.

ТЗ вычислялся на окружности x²+ y²=R1², где R1=0,8R. Полученное значение равно –10,9550

Заключение

В работе показано, что если известные вихревые лазерные пучки с радиальной симметрией (Лагерра – Гаусса и Куммера) видоизменить с помощью комплексного смещения координат, то и вид поперечного распределения интенсивности, и орбитальный угловой момент также изменятся и будут зависеть от степени асимметрии, а топологический заряд асимметричных пучков Лагерра – Гаусса и Куммера останется таким же, как у радиально-симметричных пучков, равным n. Показано также, что если известный пучок Бесселя – Гаусса с радиальной симметрией и тополо- гическим зарядом n подвергнуть гибридному преобразованию, когда Гауссов пучок остаётся без изменения, а координаты пучка Бесселя смещаются в комплексную плоскость, то у получившегося асимметричного пучка Бесселя – Гаусса топологический заряд останется равным n. Известно, что пучок Эрмита – Гаусса не несёт топологический заряд (он топологически нейтральный). Если такой пучок проходит через цилиндрическую линзу, ось которой составляет некоторый угол с декартовыми координатами, то получившийся пучок Эрмита–Гаусса (вихревой пучок Эрмита–Гаусса) будет обладать орбитальным угловым моментом, зависящим от угла поворота цилин- дрической линзы. Но, как оказалось, топологический заряд такого пучка не будет зависеть от поворота цилиндрической линзы и будет равен n. Вихревой пучок Эрмита–Гаусса является конечной суперпозицией обычных безвихревых пучков Эрмита–Гаусса. Но можно создать вихревой пучок, сложив всего два пучка Эрмита–Гаусса, например, с номерами (n, n + 1) и (n + 1, n) и с задержкой по фазе π/2.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18 -2920003, расчёт топологического заряда асимметричных оптических вихрей), Российского научного фонда (грант 18-19-00595, расчёт топологического заряда вихревых пучков Эрмита – Гаусса), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (результаты моделирования).