Топологический заряд суперпозиции одинаковых параллельных однокольцевых пучков Лагерра-Гаусса

В ряде работ изучался топологический заряд суперпозиции параллельных оптических вихрей, и в частности параллельных пучков Лагерра–Гаусса (ЛГ). Эта задача вызывала интерес ещё с 2000 года, когда в работе [1] изучались число и расположение оптических вихрей в суперпозиции двух параллельных Гауссовых пучков с внедрёнными оптическими вихрями. В [1] аналитически получено трансцендентное уравнение для определения положения оптических вихрей, но только для случая, когда вихри в обоих пучках имеют первый порядок. Показано также, что при разделении двух пучков некоторым критическим расстоянием, наряду с вихрями положительного порядка, появляются вихри отрицательного порядка. Позже в [2] c помощью анализа вилочек на интерференционной картине двух параллельных пучков ЛГ показано, что при изменении расстояния между пучками меняется расположение винтовых дислокаций в суперпозиции. Кроме того, в работе этих же авторов [3] показано, что число вихрей в суперпозиции двух параллельных пучков ЛГ может меняться при распространении в пространстве, хотя суммарный топологический заряд остаётся неизменным. В работе [4] изучается суперпозиция двух внеосевых оптических вихрей, но с ортогональной поляризацией. Вместо динамики фазовых сингулярностей, в этой работе изучается динамика поляризационных сингулярностей и положение C-точек в зависимости от расстояния между вихрями, их топологического заряда, а также фазовой задержки между ними. В [5] так- же рассматривается интерференция двух внеосевых Гауссовых пучков, но с разной кривизной волнового фронта. Получены условия, при которых формируются вихревые диполи (два оптических вихря противоположных порядков). В [6] изучается когерентная и некогерентная суперпозиция двух параллельных частично-когерентных оптических вихрей. Показано, что вид суперпозиции, расстояние между пучками, расстояние распространения и параметр когерентности влияет на число и расположение вихрей когерентности. Количество вихрей, правда, определяется только численно. В [7] рассматриваются оптические вихри, формирующиеся в суперпозиции внеосевых вихрей в нелинейном процессе трёхволнового смешивания. Установлено количество вихрей, их топологические заряды в некоторых частных случаях. В недавней статье [8] рассматривается взаимодействие параллельных пучков Бесселя–Гаусса и исследуется формирование, уничтожение и расщепление оптических вихрей в зависимости от смещения пучков от оптической оси, их топологического заряда и разности фаз между ними. Показано, что суммарный топологический заряд такого составного поля не обязательно равен сумме топологических зарядов составных пучков. В [9] показано, как рассчитывать топологический заряд (ТЗ) суперпозиции только двух параллельных пучков ЛГ. В частности, в [9] было аналитически показано, что если два пучка одинаковые, то есть имеют одинаковый ТЗ, например, m, то у суперпозиции таких пучков при любом расстоянии между ними ТЗ будет также равен m.

В данной работе мы обобщим этот результат на суперпозицию из конечного числа параллельных однокольцевых одинаковых пучков ЛГ. И покажем, что если весовые коэффициенты такой суперпозиции действительные (то есть все пучки ЛГ имеют одинаковую фазу, но могут иметь разную амплитуду), то ТЗ суперпозиции равен ТЗ каждого пучка, то есть m . Ранее уже было доказано, что нормированный на мощность орбитальный угловой момент такой суперпозиции тоже равен ОУМ одного пучка ЛГ в суперпозиции, то есть тоже m [10].

1.    ТЗ суперпозиции одинаковых параллельных пучков ЛГ в начальной плоскости

Рассмотрим суперпозицию N параллельных одинаковых однокольцевых пучков ЛГ в начальной плоскости:

E m ( x , y ) = £ с - ( e - r -^ - ) m x

“                            (1)

x exp ( - r ² - r „ ² + 2 rr n cos ( ф-ф _n ) ) .

Топологический заряд каждого пучка в (1) равен m , радиус перетяжки включен в радиальную переменную r : r / w . Предположим, что весовые коэффициенты c n в (1) являются действительными числами. Полярные координаты центров пучков ( r n , ф _n ). ТЗ суперпозиции (1) будем рассчитывать по формуле Берри [11]:

• 1    г т U ^{d E} ( ^r , ф ) / ^д Ф TC = —limIm d ф--————.

2 п ^r ^” 0        E ( r , ф )

Подставив (1) в (2), получим:

1           ^2пГ N

TC = — limIm [ £ c - ( e ) ТГ r ^Ю j          ^х

^{2 п}           0 _ - =1

- r_-e i ^ф ” ) m x exp( - r n + 2 rr_- cos ( ф - ф _- ) )

imreiф reiф_r e фn

- 2 rr - sin( ф-ф - )

x

x

N              x m                         ..I^-1           2 r_     N

£ c - ( re i ^ф - r - e i ^ф n ) exp( - r - ² + 2 rr - cos( ф-ф - )) d ф = m - — Im J £ c - r - sin( ф-ф - ) x m =1                                                              _                  ^{2 n}      0 _ - =1

x ( re i ^ф ) exp( - r „ ² + 2 rr „ cos( ф-ф _- )) I x

2r m--Im

2 n

N _m

£ c - ( re i » )” exp( - r - ² + 2 rr - cos( ф - ф - ))

m =1

-1

d ф =

²ⁿ N

J £ c - r - sin( ф - ф - ) exp( - r - ² + 2 rr - cos( ф - ф - )) 0 - =1

x

N

£ c - exp( - r - ² + 2 rr - cos( ф - ф - ))

m =1

-1

d ф = m .

В (3) мнимая часть от последнего интеграла равна нулю, так как он действительный. Из (3) следует, что ТЗ суперпозиции параллельных одинаковых однокольцевых пучков ЛГ с номерами (0, m ) равен в начальной плоскости m .

2. ТЗ суперпозиции параллельных одинаковых пучков ЛГ с разными весовыми коэффициентами в дальнем поле

В дальней зоне смещение каждого пучка ЛГ оказывается наклоном, то есть в дальней зоне пучки ЛГ становятся осевыми, но с наклонами. Поэтому комплексная амплитуда всей суперпозиции в дальней зоне имеет вид:

E m ( r , ф , z >>  z o ) = exp

m r2 )| V2.

— I —reiф

Wo2 JI Wo

Пусть в начальной плоскости имеется суперпозиция N смещённых с оптической оси одинаковых однокольцевых пучков ЛГ. Тогда комплексная амплитуда в начальной плоскости равна:

N x£ c- exp (ika-r cos ф + ikb-r sin ф),

- =1

где ( r , φ) – полярные координаты в дальней зоне. По формуле М.В. Берри [11] ТЗ равен

x exp

( x - a - ) 2 + ( y - b - ) 2 w 0²

„ / x N IV2rz

E m ( x , y ) = £ c - 1—^Г ( x - a -

- =1 I W o

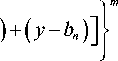
1             2 Г N

TC = —limIm [ £c- x r^^

ⁿ o - =1

x d—r exp ( ika_-r cos ф + ikb_-r sin ф ) _ x

-1

где ( x , y ) – декартовы координаты в начальной плоскости, w 0 – радиус перетяжки Гауссова пучка, ( a n , b n )– координаты центров пучков, c n – коэффициенты суперпозиции. В отличие от (1) в (4) пучки в суперпозиции взяты с комплексными весовыми коэффициентами c m и явно выделен радиус перетяжки Гауссова пучка.

x £ c „ exp( ika„r cos ф + ikbr sinф) d ф + _ - =1                                       ⁷_

1          2n^ l ( re^ ) m l

+limIm f —^ф-------- d ф.

2 n ^r ^”     ^J     ( re i ^ ) m

Сокращая в числителе и знаменателе общие множители, получим далее:

1            ²ⁿ N

TC = m +-- limIm Г У с . x

2л r ^”

^- ^п о n =1

-d-^ exp ( ika n r cos ф + ikb n r sin ф)^| x

NI x ^c exp(ika„rcosф + ikbnrsinф)

L

Второе слагаемое – это ТЗ некоторого добавочного поля вида (без Гауссовой огибающей).

N

Eadd (x, y) = £Cn exp (ikanx + ikbny).(8)

n =1

Так как числа a n , b n , c n произвольны, формула (8) может описывать широкий класс световых полей. В частности, добавочное поле может и само быть вихрем и потому давать дополнительный ТЗ. Например, если взять N =4, c 1 =– i , c 2 = 1, c 3 = i , c 4 =– 1, a 1 =– a 3 = r 0 , a 2 = a 4 =0, b 1 = b 3 =0, b 2 =– b 4 = r 0 , то получим добавочное поле вида

Eadd (x, У) = 2sin (kax) + 2 i sin (kay),(9)

которое вблизи центра равно примерно

Eadd (x ~ 0, У ~ 0 ) = 2ka (x + iy),(10)

то есть содержит вихрь первого порядка. Если же в суперпозиции (4) все коэффициенты c n вещественны, то можно показать, что

Eadd ( x, У ) = Eadd(-x, -У )•(11)

Из (11) следует, что если в некоторой точке ( x null , y null ) имеется нулевая амплитуда, то и в точке (– x null , – y null ) амплитуда также равна нулю, и вблизи нуля амплитуда комплексно-сопряженная. То есть для каждого вихря, который есть в поле (8), есть «сопряженный» вихрь, топологические заряды которых компенсируют друг друга, и поэтому ТЗ поля (8) при действительных коэффициентах c m равен нулю. Выражение (11) доказывается просто:

N

E * (u, v) = ^ cn exp (-ixu - iyv) = n=1                                               (12)

N

= ^ c n exp ( ix ( - u ) + iy ( - v ) ) = E ( - u , - v ).

n =1

Есть также физическое соображение, почему поле (8) не может иметь ТЗ, отличный от нуля. Действительно, амплитуду вида (8) формирует в Фурье-плоскости (в фокусе сферической линзы) световое поле, которое в начальной плоскости состоит из N точечных источников с разной амплитудой, но одинаковой фазой. Световое поле, амплитуда которого является действительной функцией, может создавать оптические вихри только парами с топологическими зарядами + p и – p. Это также следует из того, что оп- тический вихрь, прошедший амплитудную маску, не изменяет свой ТЗ [12, 13].

Если ТЗ суперпозиции (1) в начальной плоскости и дальней зоне одинаковый и равен m , то и в любой другой плоскости он равен m , если коэффициенты c n действительные.

3.    Моделирование

Например, на рис. 1 показаны интенсивности и фазы двух суперпозиций внеосевых однокольцевых пучков ЛГ при следующих параметрах: длина волны λ =532 нм, радиус перетяжки всех пучков – 0,5 мм, число пучков ЛГ N =4, ТЗ каждого из них m =3, декартовы координаты центров этих пучков ( a 1 , b 1 ) =( r 0 , 0), ( a 2 , b 2 ) =(0, r 0 ), ( a 3 , b 3 ) =(– r 0 , 0), ( a 4 , b 4 ) =(0,– r 0 ), где r 0 =3 w 0 , коэффициенты суперпозиции при пучках ЛГ равны c 1 = c 2 = c 3 = c 4 = 1 (рис. 1 а , б ) и c 1 =– i , c 2 = 1, c 3 = i , c 4 =– 1 (рис. 1 в , г ), расчётная область | x |, | y | ≤ R , где R =5 мм, радиус окружности для вычисления ТЗ R 1 =4,5 мм, число отсчётов по каждой координате N = 1024. Когда все коэффициенты суперпозиции одинаковы (рис. 1 а , б ), распределение фазы приобретает асимметричный вид, но общий ТЗ четырёх пучков ЛГ получился таким же, как у каждого из них: TC = 3,0042 ≈ 3. Если же подобрать коэффициенты, как на рис. 1 в , г , то, несмотря на их неодинаковость, распределение фазы симметрично относительно центра, а общий ТЗ изменился и получился равным TC = 4,0003 ≈ 4.

Рис. 1. Интенсивности и фазы двух суперпозиций внеосевых однокольцевых пучков ЛГ, у которых общий ТЗ (а, б) такой же, как у каждого пучка, или (в, г) отличается от ТЗ каждого пучка из-за наличия комплексных весовых коэффициентов в суперпозиции

При распространении в свободном пространстве четыре пучка ЛГ расширяются и начинают интерферировать друг с другом. На рис. 2 показаны интенсивности и фазы пучков с рис. 1 при тех же самых параметрах, но на расстоянии Рэлея z = z0 = kw02/2 ≈ 1,476 м. Когда все коэффициенты су- перпозиции одинаковы (рис. 2а, б), общий ТЗ четырёх пучков ЛГ остаётся равным трём: TC =2,9968 ≈ 3. Для пучка на рис. 2в, г общий ТЗ остаётся равен четырём: TC =3,9903 ≈ 4.

Рис. 2. Интенсивности и фазы двух суперпозиций

внеосевых однокольцевых пучков ЛГ, вид которых в начальной плоскости показан на рис. 1, на расстоянии Рэлея

В дальней зоне все четыре пучка ЛГ смешиваются друг с другом и распределения их интенсивности и фазы показаны на рис. 3. Все параметры расчёта те же, что и на рис. 1, но расстояние распространения z =3 z 0 ≈ 4,429 м, расчётная область | x |, | y | ≤ R , где R =7,5 мм, радиус окружности для вычисления ТЗ R 1 =7 мм, число отсчётов по каждой координате N = 2048. Когда все коэффициенты суперпозиции одинаковы (рис. 3 а , б ), общий ТЗ четырёх пучков ЛГ остаётся равным трём: TC = 2,9853 ≈ 3. Для пучка на рис. 3 в , г общий ТЗ остаётся равен четырём: TC =3,9417 ≈ 4.

а)

в)

Рис. 3. Интенсивности и фазы двух суперпозиций внеосевых однокольцевых пучков ЛГ, вид которых в начальной плоскости показан на рис. 1, на тройном расстоянии Рэлея (дальняя зона)

б)

г)

Заметим, что все пучки ЛГ в суперпозициях, показанных на рис. 1–3, имеют одинаковую мощность, хотя из теории выше следует, что ТЗ не меняется и в случае суперпозиции пучков ЛГ разной мощности, если все коэффициенты суперпозиции вещественные (пучки ЛГ складываются в фазе или в противофазе). Так, на рис. 4 показаны две такие суперпозиции. В одной из них пучки ЛГ на горизонтальной оси в два раза мощнее пучков ЛГ на вертикальной оси: c 1 = c 3 = 1, c 2 = c 4 = 1 /2 ^1/2 (рис. 4 а , б , д , е ). В другой суперпозиции мощность пучков убывает по кругу: c 1 = 1, c 2 =3 ^1/2/2, c 3 =2 ^1/2/2, c 4 = 1 /2 (рис. 4 в , г , ж , з ). Другие параметры расчёта такие же, что и на рис. 1, но расстояние распространения z =0 (рис. 4 а – г ) и z = z 0 /2 (рис. 4 д – з ). Для обоих пучков на обоих расстояниях вдоль оптической оси численно рассчитанный ТЗ оказался равен трём: TC = 3,0037 (рис. 4 а , б ), TC = 3,0017 (рис. 4 в , г ), TC = 3,0017 (рис. 4 д , е ), TC = 3,0016 (рис. 4 ж , з ).

Рис. 4. Интенсивности и фазы двух суперпозиций внеосевых однокольцевых пучков ЛГ разной мощности в начальной плоскости (а – г)

и в ближней зоне на половине расстояния Рэлея (д – з)

Заключение

Таким образом, мы доказали, что суперпозиция параллельных оптической оси одинаковых однокольцевых пучков Лагерра–Гаусса с номерами (0, m ), имеющих в начальной плоскости одинаковую фазу, но разную мощность, имеет топологический заряд, равный m , независимо от расстояния между пучками и от мощности каждого пучка. И только если у пучков разная фаза в начальной плоскости (в плоскости перетяжки), то ТЗ суперпозиции изменяется. Теоретическое рассмотрение подтверждено результатами моделирования.

Работа выполнена при поддержке Российского научного фонда (грант 22-22-00265).