Тороидальные модели магнитного поля с винтовой структурой

Выбросы коронального солнечного вещества в межпланетном пространстве называют ICME (interplanetary coronal mass ejection). Вместе с веществом выносятся солнечные магнитные петли, имеющие винтовую структуру магнитных силовых линий — MFR (magnetic flux rope). Научный интерес к исследованию MFR обусловлен тем, что MFR: 1) определяет свойства окружающей плазмы; 2) сильно влияет на распространение в межпланетном пространстве солнечных (СКЛ) и галактических космических лучей (ГКЛ); 3) при взаимодействии с магнитосферой определяет уровень геомагнитной активности. Практический интерес к исследованию MFR состоит в том, что СКЛ, ГКЛ и геомагнитная активность определяют состояние космической погоды, влияющей на безопасную работу оборудования и технологических систем, а также на деятельность человека.

Объем ICME, занятый MFR вместе с солнечным веществом, называют магнитным облаком (МО). МО занимает весь объем ICME либо его значительную часть [Marubashi, Lepping, 2007]. При исследовании процессов, протекающих в МО, необходимо использовать модель MFR. В настоящее время разработано несколько моделей MFR, имеющих различные свойства. Часто используемый метод выявления МО основан на сопоставлении прямых измерений компонент магнитного поля и модели MFR [Burlaga, 1988, Lepping et al., 1990, Farrugia et al., 1993, Leitner et al., 2007, Démoulin et al., 2008], от которой зависят результаты. К примеру, параметры МО, полученные из анализа прямых измерений на основе цилиндрической и тороидальной моделей MFR, существенно различаются [Marubashi, Lepping, 2007]: 1) ориентацией оси магнитного поля облака; 2) радиусами поперечного сечения (радиус в тороидальной модели меньше). Разные авторы используют в исследовании распространения ГКЛ в МО разные модели MFR: Кувабара и др. [Kuwabara et al., 2004] — цилиндрическую, Петухова и др. [2015] — тороидальную.

В представленной работе приведены и сопоставлены свойства пяти моделей MFR.

МОДЕЛЬ БЕССИЛОВОГО МАГНИТНОГО ПОЛЯ

В качестве модели MFR часто используют бес-силовое магнитное поле. Бессиловое магнитное поле удовлетворяет соотношению

1 X В = 0, где j — плотность электрического тока; В — напряженность магнитного поля. Отсюда следует, что ток течет вдоль поля j ~ В. С учетом уравнений Максвелла систему уравнений, определяющих бессиловое магнитное поле, можно записать в виде

V x § = а В, V § = 0, (1) где α — скаляр. В том случае, когда α является постоянной величиной или зависит от координат, поле называется линейным или нелинейным соответственно. Второе уравнение в (1) учитывает условие солeноидальности.

В реальных МО установить бессиловой характер магнитного поля затруднительно. В теоретических моделях близость магнитного поля к бессило-вому определяют по величине угла между lj и V х В : в бессиловом поле этот угол равен нулю [Vandas, Romashets, 2015] .

РЕШЕНИЕ ЛУНДКВИСТА

Решение системы уравнений (1) для бесконечно протяженного цилиндра представил Лундквист [Lundquist, 1950] . Компоненты линейного бессило-вого поля в цилиндрической системе координат имеют вид

Вр= 0, Вe= — AJр Bz = AJ°, где J0, J1 — функции Бесселя первого рода нулевого и первого порядков; A =±B0, где B0 — напряженность поля на оси цилиндра; αρ — аргумент функций Бесселя; ρ — расстояние от оси цилиндра; α=±2.41/ρ0, где ρ0 — радиус поперечного сечения цилиндра. Решение учитывает краевое условие Bz(ρ0)=0, которое получается при учете J0(2.41)=0 — приближенно первый корень J0. Репер цилиндрической системы удовлетворяет векторному произведению z6xzp=z—, где jр,z — единичные вектора. Решение Лундквиста включает четыре варианта геометрии магнитного поля: каждому значению Bz соответствуют лево- или правовинтовая спираль. На поверхности каждого цилиндра с ρ≤ρ0 располагаются винтовые магнитные силовые линии со своим шагом. Шаг винта меняется от бесконечного на оси цилиндра до нулевого на его поверхности. Напряженность поля уменьшается монотонно в два раза по направлению от оси цилиндра к поверхности.

РЕШЕНИЕ МИЛЛЕРА И ТЕРНЕРА

Миллер и Тернер рассчитали магнитное поле в торе [Miller, Turner, 1981]. При расчете использована квазитороидальная система координат, связанных с декартовыми координатами соотношениями x=(R+ρcosθ)cosφ, y=(R+ρcosθ)sinφ, (2) z=ρsinθ, где R — радиус оси тора, которая лежит в плоскости XOY; ρ — расстояние от оси тора в плоскости, поперечной оси, 0≤ρ≤ρ0, где ρ0 — радиус поперечного сечения тора; θ — угол в этой плоскости, отсчитываемый от XОY по направлению к оси Z (0≤θ≤2π); φ — угол этой плоскости, отсчитываемый от оси X к оси Y (0≤φ≤2π). Центр декартовой системы координат совпадает с центром тора. Репер квазиторои-дальной системы координат удовлетворяет векторному произведению

—j    —j     —j ieXip=Kf, где ip, ф,e — единичные вектора. Выбор репера влияет на вид оператора V в первом уравнении системы (1).

При учете симметрии вдоль оси тора ( ∂/∂ φ = 0) решение можно представить в виде

A

В. =-----Jn sin e, р  2аR 0

^В e = ^— A

J ^{1 —} 2 0 R ⁽ J ° ^{+ ар} J ¹ ) cos ^e ,

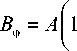
— рcose)

2 R )

J 0 .

Обозначения в (3) совпадают с обозначениями в решении Лундквиста. При R →∞ решения (3) и Лундквиста совпадают. Решение (3) является приближенно бессиловым (предполагается ρ 0 / R <<1) и удовлетворяет уравнению

V x В = а В + Н, где H — невязка. Ее можно вычислить, если подставить решение (3) в это уравнение. В результате получаем

Н = — 1.5

( aj ₀ р cos e (

—j         —j гр sin e + ie cos

^e ) /

/ R ( R + р cos e ) ) .

Решение (3) приближенно удовлетворяет условию соленоидальности

7 В = 3 AJ 1 р sin e cos e /2 R ( R + р cos 6 ) .

Используя соотношения (2), получим метрические коэффициенты h ρ =1, h θ =ρ, h φ = R +ρcosθ.

Для представления разных проекций магнитного поля либо при использовании компонент магнитного поля в расчетах, либо при сопоставлении MFR с измерениями приходится использовать решения в разных системах координат. Для определения компонент поля в нужной системе необходимо определить их в декартовой системе координат, поскольку она является связующей между различными систе- мами. Для расчета компонент магнитного поля в декартовой системе необходимо использовать связь между компонентами в разных системах. Представим линейный вектор dr в двух системах dr = — dx + L dy + Z, dz = th hd p +

X y Z p p

+ — h _ф d ф + i ₉ h ₉ d 9 .

Вычислим дифференциалы dx, dy, dz через dρ, dφ, dθ, используя (2), и подставим в это соотношение. С учетом независимости дифференциалов получим i" = i, cos 9 cos ro + i, cos 9 sin ro + i, sin 9, p X                       yZ

• — =- r sin ro + r cos ro ,

L = -— sin 9cosro- — sin 9 sin ф + iz cos 9.(4)

Представим вектор относительно двух систем координат:

—z   —z      —z      —z      —z      —z—z

B = ixBx + iyBy + izBz = ip Bp + i9 B9 + iф Bro и, используя (4), получим

B = B„ cos 9 cos ro - B,„ sin ro - B„ sin 9 cos ro, X      p                    ф9

B = B cos9sinro + B,„ cosro-B sin9sinro, y       p                       (р9

Bz = Bp sin 9 + B9 cos 9.(5)

Для определения формы магнитной силовой линии используем определение dl = Bdl / B . Здесь d Z, dl — вектор и длина элемента силовой линии; B , В — вектор и величина напряженности магнитного поля. Из определения следует:

d p = Bp dl / hp B, d 9 = B9 dl / h9 B, d ro = Bф dl / hro B.                                (6)

Построение магнитной силовой линии происходит согласно рекуррентной процедуре: выбираем (ρ, θ, φ); вычисляем согласно (3) B _ρ, B _θ, B _φ; вычисляем d ρ, d θ, d φ согласно (6); в новой точке ρ+ d ρ, θ+ d θ, φ+ d φ вычисляем B _ρ, B _θ, B _φ и т. д. Для определения силовой линии в декартовой системе используем (2) и (5).

На рис. 1, а, б представлены параметры магнитного поля для решения Миллера—Тернера. На рис. 1, а приведены распределение относительной величины напряженности поля (B/B0) в плоскости поперечного сечения тора и проекции на эту плоскость силовых линий поля, расположенных на поверхности тороидов с разными радиусами. На рис. 1, б изображены проекции силовых линий поля на плоскость XОY, расположенных на поверхности разных тороидов. Здесь в качестве тороидов обозначены тороидальные поверхности с радиусами ρT<ρ0 , вложенные внутрь тора. Видно, что силовые линии поля лежат на поверхности каждого тороида. При этом силовые линии представляют винтовые кривые с шагом, зависящим от радиуса тороида: чем меньше радиус, тем больше шаг. Отмеченные свойства являются характерными для бессилового магнитного поля. Из рис. 1, а видно, что ось поля немного смещена от центра поперечного сечения в направлении от центра тора. В то же время максимальная напряженность поля смещена к центру тора. Напряженность поля меняется в два раза. Результаты расчета, представленные на рис. 1, а–е, получены при R/ρ0=10, A=B0, α=2.41/ρ0. Возможны четыре варианта геометрии магнитного поля, так же как в решении Лундквиста. Варианты магнитного поля различаются между собой знаками компонент поля, однако на проекции силовых линий, изображенные на рис. 1, а–е, это различие не влияет.

МОДИФИЦИРОВАННОЕ

РЕШЕНИЕ МИЛЛЕРА—ТЕРНЕРА

В работе [Romashets, Vandas, 2003b] модифицировано решение Миллера—Тернера. Вводится вектор-потенциал модифицированного решения

A * m) = 1B, a где B — решение Миллера—Тернера (3). Тогда

-z ( m )    -z -z ( m )     | —z —z    1 /  —  —     -z H

B =Vx A = VxB = (aB + H ) = B + —, a a            a где B — напряженность модифицированного поля, H — невязка решения Миллера—Тернера. Используя решение (3), получим компоненты модифицированного поля

B p m ⁾

AJ 0 sin 9 ( R - 2 p cos 9 ) 2 a R   ( R + p cos 9 ) ,

B ( ^m ) =---------------P 2 a R ² J - R cos 9 x

⁹     2 a R ( R + p cos 9 ) ^{L       1}

x ( J 0 - ap J 1 ) + p (2 J 0 - ap J । ) cos² 9] ,

B Го m ) = AJ o (1 -p cos 9 /(2 R )). (7)

Обозначение величин совпадают с обозначениями в (3). Модифицированное решение также является приближенным (ρ 0 / R <<1) и точно удовлетворяет условию соленоидальности. Построение магнитных силовых линий производится так же, как в решении Миллера—Тернера.

На рис. 1, в , г , аналогичных 1, а , б , приведены параметры магнитного поля для модифицированного решения Миллера—Тернера. Из сопоставления рисунков видно, что параметры магнитного поля в решении Миллера—Тернера и в их модифицированном решении отличаются незначительно.

РЕШЕНИЕ

РОМАШЕЦА—ВАНДАСА

При расчете магнитного поля в торе использована тороидальная система координат [Romashets, Vandas, 2003a], связанных с декартовыми координатами соотношениями a sinh(ц) cos ro

= cosh( ц ) - cos n ,

_ a sinh(p)sin ф cosh(p) - cos n a sin n z =------------- cosh(ц) - cos n

.

Здесь α — параметр системы координат, который задается размерами выбранного тора ρ 0 =α/sinh(μ 0 ), R =acosh(p₀)/sinh(p₀), R /p₀=cosh(p₀), a = -JR ² -p 0 = = p₀^ ( R / p ₀ )² - 1 , где p₀ — радиус поперечного сечения тора; R — расстояние от центра тора до оси; sinh(μ), cosh(μ) — гиперболические синус и косинус. Область определения параметров: μ≥μ 0 , 0≤η≤2π, 0≤φ≤2π, где µ 0 соответствует поверхности выбранного тора.

Решение задачи можно представить в виде

Bμ=0, s cosh(p)(cosh(p) - cos n) „

B _n = - A--------------;------------F₁ ,

2 sinh³ ( ц )

B = A cosh(ц) - cos n F ф          sinh(p)      0,

где F 0 = F (α 0 , β 0 , γ 0 , ξ), F 1 = F (1+α 0 , 1+β 0 , 1+γ 0 , ξ) — гипергеометрические функции, a ₀ = ( 1 + V1 - 4 s ² ) /4, в о = ( 1 - V 1 - 4 s ² ) /4, y o =1, ^=-sinh^-2(p).

В тороидальной системе координат все поверхности с μ= const являются координатными поверхностями — тороидами. При этом поверхность с μ=μ 0 совпадает с поверхностью выбранного тора, а поверхности с μ>μ 0 описывают тороиды, вложенные внутрь выбранного тора. Поверхность с μ→∞ вырождается в ось тора. Решение (9) представляет магнитное поле, имеющее две компоненты, силовые линии которого расположены на поверхности тороидов. Величина ε определяется из соотношения F ₀(α₀, β₀, γ₀, –sinh^–2(μ₀))=0. Как видно из (9), в этом случае на поверхности тора В φ =0. Это условие аналогично использованию первого корня J ₀(2.41)=0 в решении Лундквиста.

Связь между компонентами поля в декартовой и тороидальной системах получаем из соотношения

—* —* —* —* —* —*

B = ixBx + iyBy + izBz = i, Bn+ iф Bф, где учтено, что поле в тороидальной системе имеет две компоненты (Bμ=0). Орты систем координат связаны соотношениями

— 1 I — дx — дy — дz | z = i_ 1 i.. -^ + i       , hn ( дn y дn дn J

т* _ 1 | ^— д x — д y | i i I i , ^ф h _ф( x дф y дф)

где h η =α/(cosh(μ)–cosη), h φ =αsinh(μ)/(cosh(μ)–cosη) — метрические коэффициенты. Частные производные вычисляем, используя (8). В результате получаем

B_x = B _n sinh( p ) sin n cos ф / (cosh( p ) - cos n ) -

- B ф sin Ф ,

B y = B _n sinh( p ) sin n sin ф / (cosh( p ) -

- cos n ) + B _ф cos ф ,

B z = B _n (cosh( p )cos n- 1) / (cosh( ц ) - cos n ).      (10)

Магнитные силовые линии определяем из соотношения

—*     —*     —*       —*      —*      —*

dl = idx + idy + i, dz = (iBx + iBx + i,B,) dl / B, x    y    z     xx  yy  zz где dl = dx2 + dy2 + dz2, B = Bx2 + By + Bz2.

На рис. 1, д , е показано то же, что на рис. 1, а , б . Видно, что область максимальной напряженности поля смещена к центру тора. При этом напряженность поля во внутренней области меняется в десять раз.

ИНТЕГРАЛЬНАЯ МОДЕЛЬ

Ромашец и Вандас разработали модель тороидального поля [Romashets, Vandas, 2009] , используя решение Лундквиста. Вводится образующий тор с радиусом поперечного сечения ρ₀ и радиусом оси тора R . Ось тора расположена в плоскости XОY лабораторной декартовой системы координат, а центр тора совпадает с центром системы. Вводятся вспомогательные цилиндры с радиусом поперечного сечения ρ₀, оси которых лежат в плоскости XОY и являются касательными к окружности радиуса R , центр которой совпадает с центром тора (ось тора). Магнитное поле в цилиндре и за его пределами является решением Лундквиста.

Тороидальное поле формируется суммой полей вспомогательных цилиндров с угловым размером d φ:

B x

= A

( J 1 z cos ф / p- J 0 sin ф ) d ф ,

2 ⁿ

B y = A J_Q ( J 1 z sin ф / p + J ₀ cos ф ) d ф ,

B z =- A J. ' ( ^J . ( x cos ф + y sin ф- R ) / p ) d ф , (11) где p = z ² + ( x cos ф + y sin ф- R ) 2 .

Решение Лундквиста — бессиловое поле с постоянной величиной α, все поля вспомогательных цилиндров — бессиловые поля с такой же величиной α, следовательно, линейная сумма полей (11) является также бессиловым полем с той же величиной α.

Параметры изображены на рис. 1, ж , з при R =6, α=2.41, ρ₀=1. Видно, что магнитное поле расположено за пределами образующего тора (максимальный и минимальный радиусы тора относительно его центра равны 7 и 5 соответственно), проекции силовых линий поля на поперечное сечение заметно отличаются от круговых. Напряженность поля меняется в пять раз. Параметры образующего тора не определяют однозначно форму и объем области, занятой магнитным полем. На других расстояниях компоненты поля (11) представляют магнитные поля, отличающиеся от изображенного на рис. 1, ж , з по объему и форме области.

МОДЕЛЬ

КРИТТИНАМА—РУФФОЛО

Криттинам и Руффоло представили аналитическую модель магнитного поля в петле, изображаю-

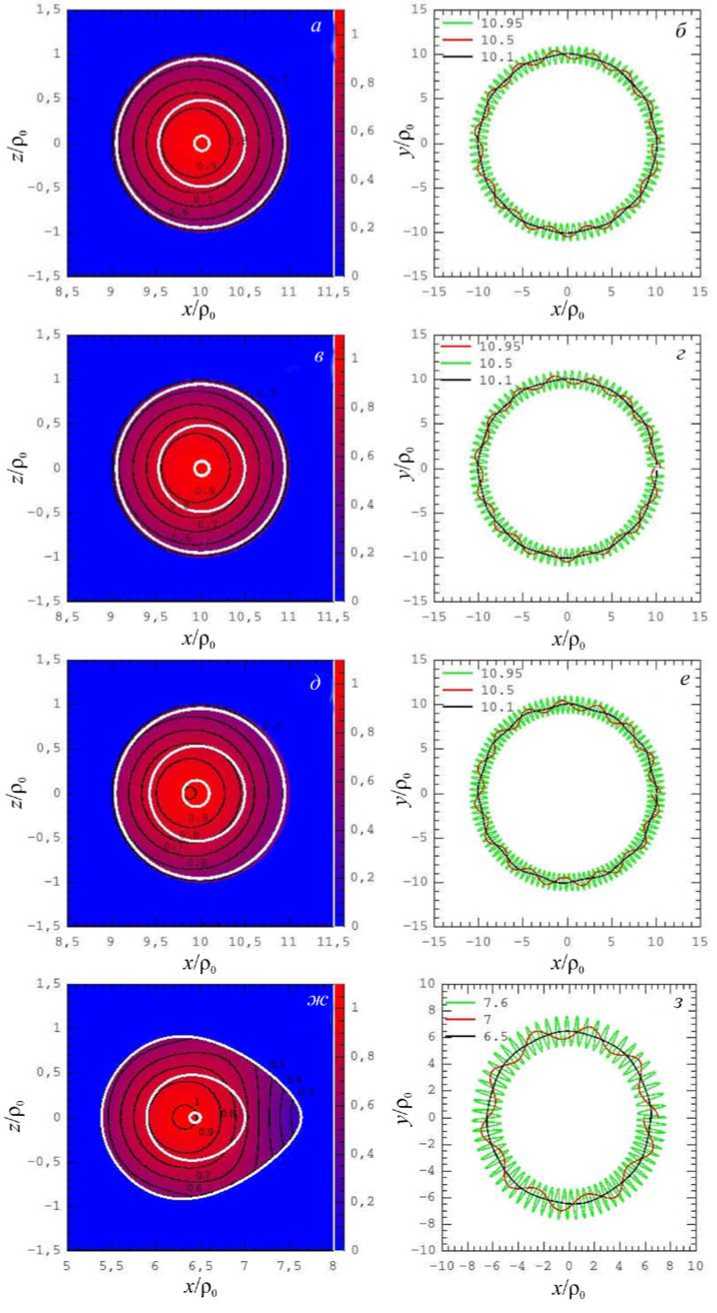
Рис. 1. Распределение относительной напряженности магнитного поля ( B / B ₀) в плоскости, поперечной оси тора, в решении Миллера и Тернера ( а ); модифицированном решении Миллера—Тернера ( в ); в тороидальном ( д ) и интегральном ( ж ) решениях Ромашеца—Вандаса соответственно. Цвет определяет величину напряженности согласно шкале, приведенной на правой стороне рисунков. Черные кривые и цифры возле них — изолинии напряженности. Белые кривые — проекции силовых линий поля для трех вариантов, различающихся x -координатой начала силовой линии. Для панелей а , в, д координаты начальной точки силовых линий у =0, z =0, x /р₀=10.95, 10.5, 10.1. Для панелей ж , з координаты начальной точки силовых линий у =0, z =0, x /р₀=7.6, 7, 6.5. На панелях б , г , е, з показаны проекции магнитных силовых линий на плоскость XOY для тех же трех вариантов. Варианты различаются цветом силовых линий, показанном в левом верхнем углу

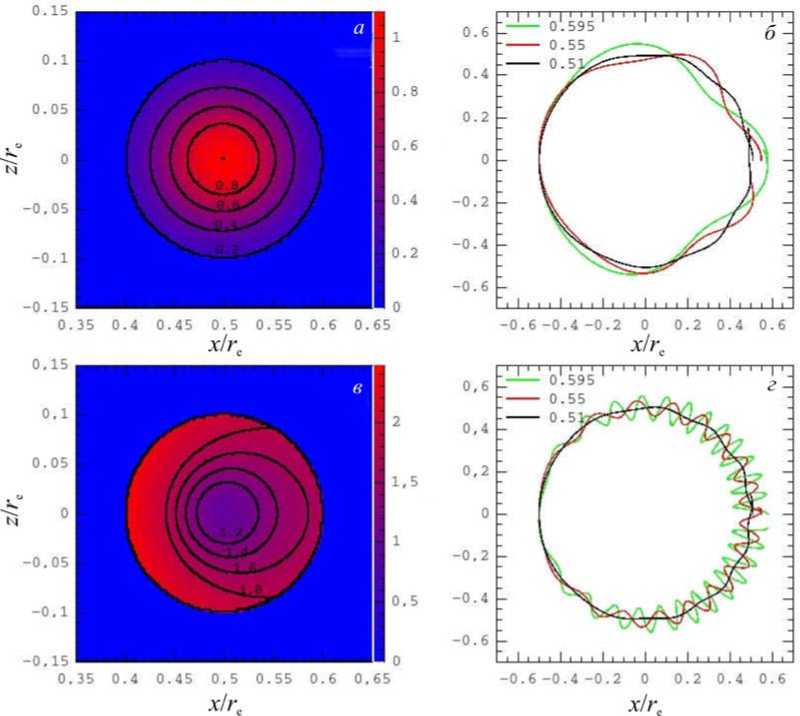
Рис. 2. Распределение относительной напряженности магнитного поля ( B / B ₀) в плоскости, поперечной оси петли ( а , в ). Цвет определяет напряженность согласно шкале, приведенной на правой стороне. Черные кривые и цифры возле них — изолинии напряженности. На панелях б , г представлены проекции магнитных силовых линий на плоскость XОY для трех силовых линий, различающихся x -координатой начала силовой линии y =0, z =0, x / r _e=0.595, 0.55, 0.51

щей МО [Krittinatham, Ruffolo, 2009]. Использована квазитороидальная система координат, как в модели Миллера—Тернера (2). В модельном расчете принято R=0.5re, ρ0=0.1re, где re — астрономическая единица. В этом случае ось при φ=π, x/re=–0.5 проходит через Солнце, а при φ=0, x/re=0.5 — через Землю. Форма магнитных силовых линий задается соотношениями р = d cos(Q / 2),

9 = wne - d / d °sin(Q /2) + 90, (12) где 0≤φ≤2π, 0≤θ≤2π, 0≤d≤ρ02π. Каждая силовая линия определяется величинами d, θ0 при φ=0. Из первого соотношения (12) следует, что площадь поперечного сечения петли стремится к нулю при приближении к Солнцу. Величина w равна полному количеству оборотов по углу θ силовой линии, расположенной вблизи оси (спиральность силовой линии). Знак w определяет лево- или правовинтовую спиральность силовых линий магнитного поля: при w>0 спиральность левовинтовая и наоборот. Экспоненциальный множитель во втором соотношении (12) посредством d0 учитывает изменение спиральности при удалении от оси. Построение силовых линий проводится так же, как в модели Миллера—Тернера. С учетом соотношений (12) вычисляем дифференциалы dρ=–(d/2)sin(φ/2)dφ, d9 = (wn / 2)e d/d0 cos(Q / 2)dф, которые используем в рекуррентной процедуре. Для расчета компонент магнитного поля учитываем связь между формой силовых линий и компонентами

В р = ( B ф / h ф ) d р / d ф ,

B9= (Bф h9 / hф) d 9 / d ф, h р = 1.

Для B _ф использовано выражение   B _ф = B ₀ /

/ [(d2 / d0 +1)3/2 cos2(ф / 2) J, которое учитывает со- хранение магнитного потока через поперечное сечение петли. С учетом первого соотношения из (12) получаем bp

в Гф),7 p

- sin I IF,

2    ( 2 J R + p cos 9

^B ф = ^B o^cos Ц J F ,

B 9 =

^B 0 w ^П _cos 2 IФI F       ^р       e -р/ [ d 0 со8( ф /2 ]

2      (2 J R + p cos 9

где F = |^р2/ d0 + cos2(Q / 2)J

На рис. 2, а, в показаны распределения напряженности магнитного поля в плоскости, поперечной оси. Проекции силовых линий представляют собой окружности с центром, совпадающим с осью. На рис. 2, б, г приведены проекции на плоскость XОY трех силовых линий, расположенных на разных расстояниях от оси. В расчете использованы значения R=0.5re, ρ0=0.1re, w=8, d0=0.07. Как видно из рис. 2, а, б, распределение напряженности поля соответствует бессиловому, тогда как распределение спиральности — нет. Если изменить знак показателя экспоненциального множителя во втором соотношении (12), максимумы напряженности и спиральности поля будут на поверхности петли (рис. 2, в, г).

ЗАКЛЮЧЕНИЕ

Приближенное решение Миллера—Тернера (ρ 0 / R <<1) описывает структуру магнитного поля в торе. Возможны четыре варианта формы силовых линий: лево- и правовинтовые спирали в разных направлениях по оси тора. Свойства магнитного поля соответствуют аналогичным свойствам поля в цилиндрической модели Лундквиста. Напряженность поля максимальна на оси тора и в два раза превышает напряженность на боковой поверхности. Спиральность поля максимальна на поверхности тора. Модифицированное решение Миллера—Тернера точно удовлетворяет условию соленоидальности. Свойства магнитного поля в решении Миллера— Тернера и в их модифицированном решении различаются незначительно. Установлено, что приближенное решение Миллера—Тернера достаточно хорошо соответствует точному решению бессилового поля в торе до ρ 0 / R ≤0.5 [Vandas, Romashets, 2015] .

Существенно асимметричное распределение параметров магнитного поля получается в тороидальной модели Ромашеца—Вандаса. Асимметрия распределения сильно зависит от величины R /ρ 0 : при ее уменьшении асимметрия возрастает. В интегральной модели результирующее магнитное поле выходит за пределы образующего тора, распределение напряженности поля сильно неоднородно. Параметры образующего тора не определяют однозначно объем и форму области, занятой магнитным полем. На других расстояниях компоненты поля (11) представляют магнитные поля, отличающиеся от изображенного на рис. 1, ж , з по объему и форме области. В аналитической модели Криттинама—Руффоло представлены компоненты магнитного поля в петле, изображающей магнитное облако. Площадь поперечного сечения петли стремится к нулю при приближении петли к Солнцу. Магнитные силовые линии имеют лево- или правовинтовую спиральность. Напряженность магнитного поля и спиральность силовых линий уменьшаются в направлении от оси петли к ее поверхности.

Для описания магнитных полей в МО лучше подходят тороидальные модели Миллера—Тернера и Ромашеца—Вандаса.

Реализованные программные коды для пяти моделей магнитного поля с пояснениями доступны на [], DOI: 10.5281/zenodo.1728477. При использовании кодов необходимо ссылаться на данную статью.

Работа выполнена при финансовой поддержке гранта Российского фонда фундаментальных исследований № 18-32-0064 мол_а, Министерства образования и науки Российской Федерации и Сибирского отделения Российской академии наук (Проект II.16.2.2.).