ТРАНСФОРМАЦИЯ КОМБИНАЦИИ ДЛЯ РАЗЛИЧНЫХ ДЛИН КОДА В ПРОЦЕССЕ ПЕРЕСТАНОВОЧНОГО ДЕКОДИРОВАНИЯ

Основной характеристикой современных интеллектуальных систем измерения и управления является их интеграция в телекоммуникационные технологии. Важнейшими аспектами этого процесса являются разработка беспилотных транспортных средств, управление роботами, дистанционное наблюдение и навигация. В ближайшем будущем значительное внимание будет уделено методам проектирования систем управления для сложных динамических объектов. В таких системах управление невозможно отделить от измерений и сопоставления реальных параметров с целевыми значениями, что необходимо для снижения степени неопределенности. В этом случае знание комбинаторных особенностей перестановок символов кодовых векторов играет важную роль в реализации алгоритма их декодирования, который во многом опирается на орбитальную структуру представления перестановок [1–5]. Особое внимание следует уделить работе с множеством непроизводных решений [6–9].

Процесс трансформации непроизводительных комбинаций (НПН) к производительному виду (ППН) является важнейшей составляющей перестановочного декодера. Целью работы является разработка оптимальных алгоритмов трансформации элементов множества непроизводных пе-

рестановок к множеству производных перестановок в системе перестановочного декодирования и оценка временных рамок выполнения процессов.

Назначение перестановок в множестве непроизводительных комбинаций

Эффективность системы перестановочного декодирования (ПД) неразрывно связана с числом кодовых комбинаций, с которыми может работать декодер. Как показано в таблице 1, для любого двоичного кода наблюдаются комбинации, которые не могут породить информационную обратную матрицу, используемую для восстановления изначального вектора, вследствие нулевого значения детерминанта. В простом случае – такие комбинации можно было бы исключить из системы ПД, и выдавать отказ, каждый раз, когда декодеру приходилось бы работать с комбинацией из непроизводного множества.

Если мы принимаем такое решение, то с увеличением длины кода мы будет сталкиваться с отказами все чаще, что неприемлемо для современных систем связи, требующих быстродействия и надежности. Выходом из ситуации служит разработка алгоритмов быстрой трансформации комбинации НПН к ППН [10]. Концепция трансформации следующая: в когнитивной карте НПН в формате ключ-значение хранится информация о непроизводительных перестановках, это такие символы, произведя замену которых на условленных позициях исходной НПН комбинации, новая комбинация, образованная перестановкой, не покинет множество НПН, а перейдет в другую непроизводную комбинацию.

Таблица 1. Соотношений производительных и непроизводительных образующих комбинаций кодов разных размеров

Используемый код	ППН	НПН
Хэмминга код (7, 4, 3)	80	20
Код БЧХ (14, 5, 7)	56	44
Код БЧХ (15, 5, 7)	62	38
Код БЧХ (15, 7, 5)	51	49
Код Голея (23, 12, 7)	52	48
Код Голея (18, 7, 7)	52	48

Поскольку образующие комбинации обриты (ОКО) цикличны, и всегда начинаются с единицы, то рационально замене подвергать последние позиции комбинации, так, при восстановлении лексикографического порядка новой комбинации – мы заведомо перейдем в другое ОКО, так как будет соблюдено свойство ОКО – единица на первой позиции. В качестве кандидатов для перестановки будут выступать позиции принятого сообщения, отсортированные по убыванию их индексов надежности [11; 12]. В работе будет подробно показан процесс трансформации НПН к ППН на примере кодов БЧХ (15, 5, 7) и БЧХ (15, 7, 5) (Коды Боуза – Чоудхури – Хоквингема).

Трансформация непроизводительных комбинации к производительному виду для кода БЧХ (15, 5, 7)

В процессе разработки карты НПН кода БЧХ (15, 5, 7) было определено несколько свойств, так, например, у ряда элементов НПН множество запрещенных перестановок последней позиции представлено всеми элементами проверочной части. Для таких элементов следует производить замену последних двух элементов для трансформации НПН в ППН. Также существуют пары элементов, замена на которые последних двух позиций НПН не приводит к трансформации в ППН.

На тестовой модели работы декодера, запущенной на процессоре с тактовой частотой 3,6 ГГц была произведена тестовая отправка десяти тысяч сообщений, закодированных с применением кода БЧХ (15, 5, 7), и было получено следующее распределение, показанное в таблице 2 и отраженное на рисунке 1.

Процесс трансформации можно описать в виде алгоритма:

• 1.    Декодер находит в карте НПН исходную комбинацию и принимает на основании этого факта решение о том, что трансформация необходима.

• 2.    На основании данных, полученных на приеме комбинации, декодер получает список запрещенных для перестановки групп символов.

• 3.    Из запрещенного списка групп, получаем группы, которые могут быть использованы для перестановки на позиции нового ОКО.

• 4.    Осуществляем перестановку путем замены нужного числа последних позиций кодового вектора на значения, полученные из списка пригодных для перестановки групп.

• 5.    Вектор после перестановки символов заново сортируется по возрастанию, чтобы удовлетворять свойствам ОКО.

• 6.    Происходит поиск в когнитивной карте (КК) ППН по новому значению ОКО, полученный объект КК передается дальше, для реализации дальнейшего процесса декодирования.

Таблица 2. Результаты декодирования 10000 сообщений декодером ПД кода БЧХ (15, 5, 7)

Позиции, которые потребовали замены	Число комбинаций	Время на перестановку
		max, мс	min, мс	avr, мс
Последний символ	2973	6,796	0,052	0,144
Последние два символа	620	14,389	0,245	0,710

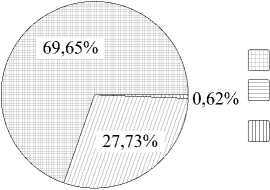
Принято без ошибок

Потребовалась замена последнего символа Потребовалась замена последних двух символов

Рисунок 1. Распределение результатов работы декодера ПД по декодированию 10000 сообщений кода БЧХ (15, 5, 7)

Трансформация непроизводительных комбинации к производительному виду для кода БЧХ (15, 7, 5)

На тестовой модели работы была произведена аналогичная отправка десяти тысяч сообщений, закодированных с применением кода БЧХ (15, 7, 5), получено распределение из таблицы 3 и показано на рисунке 2. Как видно из таблицы 3, по сравнению с кодом БЧХ (15, 5, 7) в БЧХ (15, 7, 5) помимо замены последнего и последних двух символов, замене также подвергаются и более объемные группы символов.

Описанный ранее алгоритм трансформации справедлив и для этого кода, и поскольку признак требуемой замены символов хранится в КК НПН, то декодеру в момент трансформации нет нужды в вычислении требуемого числа позиций перестановки.

Таблица 3. Результаты декодирования 10000 сообщений декодером ПД кода БЧХ (15, 7, 5)

Позиции, которые потребовали замены	Число комбинаций	Время на перестановку
		max, мс	min, мс	avr, мс
Последний символ	3232	11,422	0,07	0,146
Последние два символа	1440	13,416	0,152	0,299
Последние три символа	531	17,199	0,203	0,421
Последние четыре символа	23	17,246	0,318	1,241

Сравнение результатов тестовой отправки сообщений

При равных настройках канала связи, исходя из визуализации на рисунках 1 и 2, можно понять, что в реальной системе связи, соотношение ППН/НПН, показанное в таблице 1, будет непосредственно влиять на процент правильно принятых сообщений и решений о перестановках символов, принятых декодером.

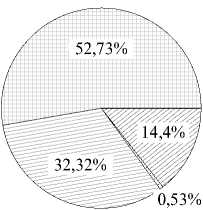
Принято без ошибок Потребовалась замена последнего символа Потребовалась замена последних двух символов 0,02%

Потребовалась замена последних трех символов Потребовалась замена последних четырех символов

Рисунок 2. Распределение результатов работы декодера ПД по декодированию 10000 сообщений кода БЧХ (15, 7, 5)

Как видно из таблиц 2 и 3, увеличение числа позиций для замены не вызывает резкого увеличения количества времени на выполнение процедуры замены позиции в комбинации, что в теории позволяет применять данный подход и для кодов с более смещенным в сторону НПН отношением ППН/НПН. Кроме того, использование сокращенных кодов, как в случае с кодом

БЧХ (14, 5, 7), как отмечено в таблице 1, также может вести к смещению отношения производительных комбинаций в сторону непроизводительных. В таком случае, эффективные методы трансформации комбинации также будут занимать ведущую роль в реализации ПД.

Заключение

В работе были продемонстрированы подходы к исправлению непроизводительных комбинаций для кодов БЧХ разной длины. Приведены временные выкладки, позволяющие судить о линейном увеличении сложности операций выполнения перестановок, в зависимости от длинны кода и общего числа требуемых перестановок, что говорит о применимости данного метода для более объемных кодов.