Трансформация структурированного света и управление орбитальным угловым моментом в трёхвитковой оптической змее

За последние десятилетия значительно вырос интерес к исследованиям световых полей с выраженной поперечной структурой распределения фазы, поляризации и интенсивности, получивших обобщающее название «структурированный свет» [1, 2]. Появление надёжных и доступных средств создания структурированного света: пространственных модуляторов света [3], геометрических фазовых элементов [4, 5] и других – позволило структурированным пучкам стать неизменным объектом исследований. Являясь интересным физическим объектом с точки зрения фундаментальной теории, структурированный свет имеет и сугубо прикладное значение. Его использование позволило достигнуть существенных успехов в областях лазерной обработки материалов [6], оптического микроманипулирования [7, 8], зондирования [9] и многих других [10]. В плане применения структурированных пучков, пожалуй, наиболее перспективной видится область информационных технологий, где в качестве носителей информации предложено использовать т.н. оптические вихри (ОВ) [11 – 13]. Особенностью ОВ является то, что они обладают собственным орбитальным угловым моментом (ОУМ), что позволяет использовать орбитальные степени свобо- ды для повышения информационной пропускной способности линий связи. Заметим, что многомерный подход к кодированию информации также открывает новые возможности в области квантовой криптографии [14, 15].

Наиболее надёжным и защищённым от внешних возмущений средством передачи структурированного света на большие расстояния представляется оптическое волокно. На сегодняшний день хорошо известна способность оптических волокон поддерживать стабильное распространение структурированного света [16, 17]. Для оптоволоконной связи с использованием ОУМ-состояний желательно иметь полностью волоконные устройства управления их характеристиками: топологическим зарядом (ТЗ), ОУМ и спиновым угловым моментом (СУМ). Кроме того, желательно обладать возможностью компенсации дисперсии для импульсов структурированных оптических полей, которая может быть выполнена за счёт использования линий задержки. Как известно из классических работ, проблему управления дисперсией в линиях связи на одномодовых волокнах можно решить с помощью ряда волоконно-резонаторных систем: SCISSOR [18], CROW [19] и микрокатушечных резонаторов (МКР) или оптических змей (ОЗ) [20–22]. Последний тип волоконных резонаторов кажется наиболее привлека- тельным из-за его уникальной трехмерной структуры, которая обеспечивает совместимость с другими устройствами и повышенную компактность. Геометрия МКР позволяет проявлять топологические фазы [23] и реализовывать сенсорные приложения [24]. Недавно сообщалось о способности МКР с двумя витками осуществлять сверхэффективное параметрическое управление ТЗ, ОУМ и СУМ проходящего структурированного света [25]. В указанной работе, однако, количество витков исследуемой ОЗ было минимально возможным – равным двум. Тем не менее, желательно исследовать влияние увеличения числа витков резонатора на его трансмиссионные свойства, по аналогии с изучением МКР на одномодовых волокнах [21].

В этой связи целью настоящей работы является исследование прохождения некоторых типов структурированных пучков, а именно ОВ и мод Лагерра– Гаусса (ЛГ) без ОУМ, через трёхвитковый МКР. С этой целью разработана векторная теория ОЗ с тремя витками, которая учитывает спин-орбитальное взаимодействие (СОВ) в волокне. На основе полученных нормальных мод такой системы и их спектров было изучено влияние её параметров на угловой момент (УМ) прошедших полей. Показано, что трёхвитковый МКР на многомодовых волокнах может сверхэффективно изменять ТЗ и УМ входящего поля. Данные процессы сопровождаются различными модовыми конверсиями. Также показано, что трёхвитковые МКР позволяют создавать на их основе линии задержки для ОВ и реализовывать перестраиваемые логические X и Y вентили Паули для световых пучков с ОУМ.

• 1.    Модель и нормальные моды трёхвиткового МКР

Схема трехвиткового МКР представлена на рис. 1. Следуя предыдущим работам, будем считать, что спиральная сердцевина имеет показатель преломления n co и окружена бесконечной средой с показателем преломления n cl . Определим в каждом витке продольную координату z вдоль центральной линии так, чтобы точки, расположенные на прямой, параллельной оси МКР, имели одинаковое значение z (см. рис. 1). Полярные координаты ( r , ф ) стандартным образом вводятся в поперечном сечении сердцевины волокна, из которого сделан резонатор. Кроме того, справедливо неравенство 0 ≤ z ≤ s , где s – длина витка.

Следуя [25], представим систему в виде трёх параллельных идеальных волокон (рис. 2). Выходные концы первого и второго волокон соединены со входными концами второго и третьего волокон соответственно; точечные линии показывают воображаемый путь света от одного волокна к другому, приращения фазы вдоль них отсутствуют. Таким образом, задача о трёхвитковом МКР сводится к задаче о трёх связанных волокнах. Будем использовать подход, развитый в [26], для решения векторного волноводного уравнения для параллельных многомодовых волокон:

[V 2 + к ² n ² ( x , y ) + V t V t ln n ² -J e t ( x , y ) = P ² e t ( x , y ) , (1)

где n – показатель преломления системы, k – волновое число в вакууме, V t = ( d / d x , d / d y ) , и в - постоянная распространения. В качестве базиса выбраны ОВ | m ) , локализованные на соответствующих волокнах (витках):

• 1 1)    = |1, /,1);| 2) = |1, - /,1);| 3) = |- 1, - /,1);

• 14)    = |- 1, /,1);| 5) = |1,/,2);|б) = |1, - /,2);

• 17)    = |- 1, - 1,2); |8) = |- 1, - /,2); |9) = |1, /,3);

• 1 10)    = |1, - /,3);|11) = |- 1, - /,3);|12) = |- 1, - /,3).

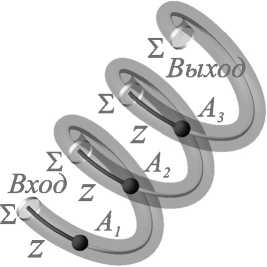
Рис. 1. Схема трёхвиткового МКР. Кружки S обозначают границы между витками. Продольные координаты z введены в каждом из витков по отдельности таким образом, что точки A1, A2 иA3, которые лежат на одной линии, параллельной оси МКР, имеют одну и ту же координату z

б)

о

о

Рис. 2. (а) Эквивалентная схема трёхвиткового МКР.

Система представлена в виде трёх параллельных волокон с единой продольной координатой z. Поля на выходных концах крайнего левого и центрального волокон совпадают с входными полями центрального и крайнего правого волокон соответственно. Красные пунктирные линии показывают условный путь света от выхода из одного волокна ко входу другого волокна. (б) Распределение показателя преломления в плоскости, ортогональной оси эквивалентного массива волокон; расстояние между центрами волокон определяется величиной Лго, где Л > 2

Поля (2) представлены в базисе линейных поляризаций: |e) = col(ex, ey); кет-векторы расшифровываются следующим образом: |а,l,j) = col(1, ia)exp(ilфj)F^(rj), где l = ±λ,λ= 0, 1,2 является ТЗ. Индекс «j» полярных координат (rj, фj) указывает на номер связанного волокна, Fλ– радиальная функция для идеального волокна со ступенчатым профилем [27], а = ± 1 определяет знак круговой поляризации. Для введённых базисных векторов подразумевается следующая нормировка: {а, l, j | v, m, i) = 5аv 5m 5j, скалярное произведение определено как:

'T,Y~ от* Ф2)i 1 ds,

¹ V^ 2 )

I - площадь полного поперечного сечения волокна, 5 _im - дельта-символ Кронекера. Выбранная в данной работе нормировка указывает на то, что используется приближение слабой ортогональности, чего не было в работах [25, 28]. Как было показано в этих работах, сильная связь в задачах о связанных волокнах приводит не к изменению структуры мод, а к модификации постоянных распространения нормальных мод. Поэтому общая картина модовой конверсии принципиально не меняется, что оправдывает использование упрощённого подхода.

Для получения структуры нормальных мод трёх параллельных волокон в предлагаемой парадигме теории возмущений с вырождением [26] необходимо в базисе (2) построить матрицу H оператора, находящегося в левой части (1). Тогда нормальные моды | ^ а ) могут быть найдены по решениям Х _а = col( x _{а 1} ,... x _{а 12} ) уравнения на собственные векторы НХ _а = в ² Х _а как:

альных ОВ | а , l , j ) . При построении матрицы H учтено, что связь учитывается только между соседними волокнами.

Спектр и собственные векторы матрицы H находятся путем её диагонализации, проводимой в два этапа. На первом этапе выполняется преобразование H >« H М + , где

М= ¹

' C

0 4 C 0 4

0 4V E 4

⁰ 4 V² E 4

2 E 4

— 2 E 4

E 4

— V2 E ₄

E 4 J (6)

| ^а) = Е x а Дк У k

В нашем случае матрица возмущений H имеет вид:

^

^-

P t   Q t + ^в E 12 ,

где в _t - скалярная постоянная распространения, E_m и O m – единичные и нулевые матрицы ранга m соответственно, матрицы P λ и Q λ имеют следующий вид (выражения для их элементов приведены в дополнении):

P t =	' A ‘ 0	0 B t	0 0	0 ^ B t 5 t 1
	0	0	A t	0		,
	V 0 ' C t	B t 5 t 1 D t	0 0	B 0 ^	t >	(5)
Q t =	D t 0	C t 0	0 C t	0 D '
	V 0	0	D t	C < ,

Матрица P λ позволяет учесть СОВ в отдельном волокне, а матрица Q λ – межволоконную связь парци-

1 ' ^E 2 ^E 2 ^

72 V E 2 — E 2 /

Матрица H после преобразования приобретает блочно-диагональный вид, при котором на главной диагонали находятся матрицы второго ранга. Затем каждая из этих матриц диагонализируется стандартным образом. На диагонали конечной матрицы 12 ранга находится спектр Ав ² , где Ав ² = в ² — в ² . Здесь в i - точная постоянная распространения, а в l - скалярная постоянная распространения [27].

2. Преобразование структурированного света

Существует два способа теоретического изучения преобразований поля, входящего в катушечные резонаторы. Первый из них требует составления системы дифференциальных уравнений относительно медленных амплитуд [21, 29]. В настоящей работе используется схема, которая позволяет вместо системы дифференциальных уравнений решать систему линейных алгебраических уравнений относительно X i – коэффициентов разложения возбуждаемого в МКР поля | Т f ) : |Т f ) = £ 1 = 1 X, | V i ), где | ¥ i ) - нормальные моды, выражения для которых легко могут быть получены на основе собственных векторов (А1) матрицы Н . Процедура получения такой системы уравнений описана в [25]. В дальнейшем будем предполагать, что при разложении поля | V f ) нужны моды только с одинаковым орбитальным индексом l . При этом входящее и выходящее поля | ^ in ) и | ^ out ) представляются в виде суперпозиции ОВ | а, l ) : | V in ) = S C а, i | а, l \ | V out ) = S k а, l | а, l ) соответственно. Отметим, что в данных выражениях в кет-векторах справа опущен за ненадобностью третий индекс. Мощность, запасённая в парциальных вихрях выходящего поля, вычисляется тогда следующим образом: T _т, l = | к а, l | ² . Также выполняется закон сохранения энергии: S | C а, l | ² = S | к а, l | ² .

В отличие от МКР на одномодовых волокнах, МКР на многомодовых волокнах могут влиять не только на фазу и поляризацию передаваемого поля, но и на его модовое состояние [25, 30]. К числу наиболее интересных типов структурированных световых полей, подверженных трансформации в МКР, относятся различные типы ЛГ-мод, которые на вход-

ном торце волокна (при соответствующем согласовании радиуса перетяжки и других параметров) могут быть аппроксимированы линейными суперпозициями ОВ | а, l ). В частности, они включают в себя циркулярно поляризованные (ЦП) ЛГ-пучки вида (|с , ^)±|о , -l) ) / V2 или их линейно поляризованные (ЛП) аналоги (| о, 1 )± | а, - 1 ) +|- а, 1 )± |- о, - 1 ) )/2 (они же являются стандартными ЛП-модами идеальных волокон в скалярном приближении). В качестве отдельного случая таких пучков принято выделять пучки с фазовой сингулярностью, а именно ОВ | а, l ) [2]. Поскольку пучки Эрмита–Гаусса (ЭГ), как правило, лишены осевой симметрии, их преобразования в оптических волокнах традиционно не исследуются. Тем не менее, в случае λ = 1 ЛП и ЦП ЛГ-пучки обладают одинаковой симметрией с ЭГ-пучками, поэтому можно говорить об ЭГ-подобных пучках при рассмотрении несингулярных ЛГ-пучков с орбитальным числом λ = 1. В дальнейшем мы изучим случай λ = 1 отдельно от случая λ > 1 из-за различий в структуре нормальных мод с λ = 1 и λ > 1.

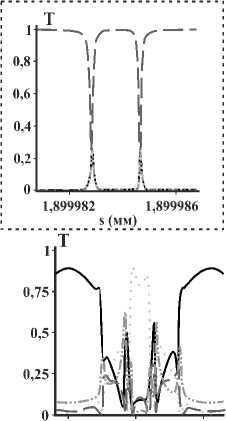
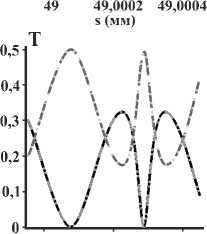
Первый тип модовой трансформации, который мы изучаем, демонстрирует инверсию ТЗ входящего ОВ. На рис. 3 а,б,в приведены кривые мощности парциальных ОВ | а, l ) в выходящем поле, когда входящим полем является ОВ 1 1,1) . Из рис. 3 а очевидно, что изменение длины витка в пределах микрометра приводит к инверсии ТЗ выходящего поля. Таким образом, можно сделать вывод, что трёхвитковая ОЗ пригодна для сверхэффективного параметрического управления ТЗ. Ещё одним интересным явлением, связанным с распространением полей с азимутальным числом λ =1, является так называемый спин-орбитальный резонанс (СОР), при котором мощности выходящих парциальных ОВ при некоторых длинах витка ОЗ уравниваются. На вставке к рис. 3 а приведён пример данного явления. Заметим, что СОР не существует в МКР на мономодовом волокне. На рис. 3 б,в продемонстрировано, что МКР при определенных параметрах способен преобразовывать падающий ОВ | 1,1) в другие ОВ: |- 1, - 1) и |- 1,1) , влияя также на состояние поляризации. Для группы полей с азимутальным числом λ =1, падающих на входной торец МКР, СОР представляет собой обычное явление. Действительно, на рис. 3 г продемонстрированы СОР для выходящих полей в случае, когда МКР возбуждён ТМ-модой |TM^ = ( 1, — 1 +1- 1,1) ) / V2 . Очевидно, что точки пересечения дважды вырожденных кривых для мощностей ОВ являются точками СОР.

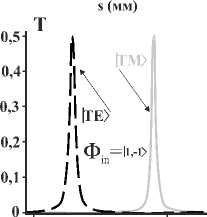
Трёхвитковые ОЗ также способны генерировать такие типы цилиндрических векторных пучков (ЦВП) [6], как ТМ- и ТЕ-моды (|TE) = (| 1,-1) -|-1,1)) /72). Данный тип генерации наблюдается при прохождении через резонатор ЭГ-подобных пучков или ОВ. ЦВП такого вида имеют практическое значение, поскольку, в отличие от других ЦВП, они могут быть жёстко сфокусированы, что выгодно на практике в ряде случаев. На рис. 3д показаны зависимости мощности T ТМ- и ТЕ-мод от длины s витка при возбуждении МКР ОВ |1,-1). Заметим, что мощности T

б)

90,6172 90,6174 90,6176

0,9998      1      1,0002       1,899982         1,899985

г)                                д)

—|1,1> -- |1,-1> —-И,-1>   И, 1>

Рис. 3. Мощности Т выходящих полей (в единицах мощности входящего поля), прошедших трёхвитковый МКР, с азимутальными числами λ= 1: (а, б, в) входящее поле ОВ 11,1); (г) входящее поле TM-мода; (д) входящее поле ОВ 11,-1). Панели (а-г) - мощности T, приходящиеся на парциальные ОВ | р; l) в зависимости от длины s витка.

Панель (д) показывает мощности T, запасённые в выходящих TM- и TE-модах. Параметры: Л = 2,15, го = 8Ло, nco=1,5, Л = 5-10 -3,Ао = 632,8 нм можно вычислить как: T = |{TM(TE )| Vout)|2. Из рис. 3д видно, что эффективность генерации ЦВП с помощью МКР не превышает 50%, и оставшаяся мощность запасена в ОВ 11,1) и |1,-1). На практике сортировка ТМ- и ТЕ-мод осуществляется при сильной фокусировке: данная процедура менее эффективна для парциальных ОВ |1,1) и |-1,-1). Рис. 3д также демонстрирует, что МКР пригодны для сверхчувствительного параметрического переключения между режимами генерации ТМ- и ТЕ-мод.

Очевидно, что 3-витковые МКР делают возможной как генерацию, так и сверхэффективное параметрическое управление ОВ в случае подачи в них регулярных пучков. Также понятно, что при постоянной длине витка изменение длины оптического пути может быть достигнуто за счет изменения длины волны

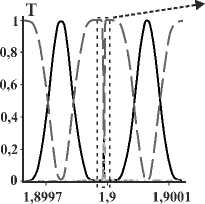
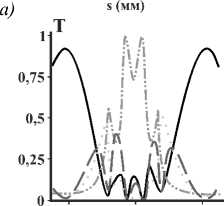
λ. На рис. 4а показана зависимость мощности прошедшего ОВ |1, 5〉 от длины волны λ в случае, когда МКР возбуждается полем (1,5 +1,-5 )/V2 . Необходимо отметить, что при λ> 1 нормальные моды расцеплены по состоянию поляризации, поэтому МКР не изменяет состояние поляризации, и выходящее поле состоит только из ОВ |1, 5〉 и |1,–5〉. Заметим, что на рис. 4а не приведены трансмиссионные кривые для ОВ с противоположным ТЗ, так как сумма мощностей выходящих ОВ равна единице. На этом же рисунке заодно показана кривая мощности ОВ |1, 5〉 для случая МКР с двумя витками. Видно, что модуляция мощности ОВ |1, 5〉 сильнее в случае трёхвиткового МКР. Важное отличие ОЗ на многомодовом волокне от ОЗ на одномодовом волокне состоит в том, что пиковые значения мощности Т не обязательно достигают единицы, данный факт был ранее объяснён в [25]. На рис. 4б приведены кривые прохождения для ОВ |1, 5〉 и времени td групповой задержки (ВГЗ) для него, где td =– dΦ /dω [31], Φ – фаза парциального ОВ, ω – частота; на вход волокна подаётся ОВ |1, 5〉. Оценка ВГЗ тесно связана с актуальной проблемой создания линий задержки [32], необходимых для компенсации дисперсии. Следует подчеркнуть, что для случая многомодовых волокон задача о ВГЗ не сводится автоматически к задаче о нахожде- нии максимального времени задержки, как в случае одномодовых волокон. Это связано с тем, что в МКР на многомодовом волокне существует два ОУМ-канала для ортогональных состояний |1, ±5〉, между которыми перераспределяется входная мощность. Поэтому недостаточно достигнуть максимального значения ВГЗ, например, для канала |1, 5〉. Одновременно необходимо следить за тем, чтобы мощность, передаваемая по этому каналу, была достаточно большой. На рис. 4б приведены соответствующие кривые, которые доказывают существование спектральных областей, где максимальное ВГЗ совпадает с максимальной мощностью в канале. Соображения симметрии говорят также о том, что кривые для коэффициента прохождения ОВ |1,–5〉 и ВГЗ для него будут точно такими же в случае, когда на вход МКР будет подан ОВ |1,–5〉. Таким образом, можно утверждать, что МКР на одной и той же длине волны могут одновременно служить элементами линии задержки для ОВ |1, 5〉 и |1,–5〉. На рис. 4в приведены кривые для выходящей мощности ОВ |1, 5〉 и его ВГЗ при наличии в системе затухания, которое вводится при помощи замены β → β + iγ, где γ – коэффициент затухания. Из данного рисунка видно, что наличие затухания приводит к уменьшению мощности выходящего поля и сильному уменьшению ВГЗ.

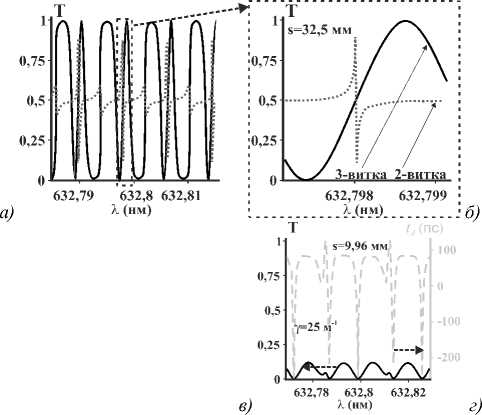
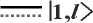
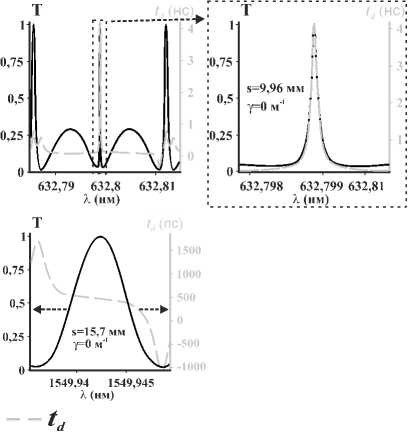
Рис. 4. (a) Зависимость мощности выходящего ОВ | 1, 5〉 (в единицах мощности входящего поля) для 2-виткового (точечная синяя кривая) и 3-виткового (сплошная красная кривая) МКР; МКР возбуждается ЛГ-пучком ( 1,5 + 1, - 5 ) / 2 ,

s =32,5 мм. (б) Выходящая мощность (в единицах мощности входящего поля, сплошная красная кривая) и ВГЗ t d (пунктирная зелёная кривая) ОВ | 1, 5〉 для 3-виткового МКР, возбуждаемого ОВ | 1, 5〉 . (в) Выходящая мощность Т ОВ | 1, 5〉 (в единицах мощности входящего поля, красная сплошная кривая) при наличии затухания и ВГЗ (пунктирная зелёная кривая) для 3-виткового МКР, возбуждаемого ОВ | 1, 5〉 . (г) Аналог рис. 4б, выполненный для телекоммуникационных частот. Параметры: r 0 =10 λ 0 , (а,б,в): λ 0 = 632,8 нм, (г) λ 0 =1550 нм, остальные такие же, как для рис. 3

Отдельно нужно обратить внимание на возможность использования МКР в линиях связи. Для передачи данных на несущей частоте ω нужно промодулиро-вать входящий сигнал с некоторой частотой Ω << ω. Например, при гармонической модуляции амплитуды возникает три волны с частотами ω – Ω, ω и ω + Ω. Если при частоте ω – Ω, на которой передаётся полезный сигнал, входящий ОВ будет полностью инвертироваться резонатором, передача данных по соответствующему каналу станет невозможной. Для случая, про- иллюстрированного рис. 4б, при указанной амплитудной модуляции (АМ) с частотой Ω ≈ 50 МГц уровень мощности выходящего ОВ будет примерно держаться на уровне 0,7 (в единицах мощности входящего ОВ). Тем не менее, частота 50 МГц существенно меньше частот модуляции от 2,5 ГГц до 10 ГГц, используемых в современных волоконных линиях связи с плотным мультиплексированием по длине волны. Частично исправить ситуацию можно с помощью масштабирования оптической змеи по отношению к длине волны. Если выбрать радиус r0 сердцевины волокна равным 10λ0, где λ0 =1550 нм, и длину витка s = 15,7 мм при остальных параметрах, как под рис.3, и передавать данные вблизи этой длины волны λ0, то уровень мощности выходящего ОВ |1, 5〉 не будет падать ниже 0,7 при частотах модуляции около 0,5 ГГц. Данный пример демонстрирует принципиальную возможность использования МКР в современных линиях связи. Необходимо отметить, что за увеличение частоты модуляции приходится «платить» уменьшением ВГЗ (рис. 4г).

3. Управление спиновым и орбитальным угловыми моментами

Несмотря на многочисленные исследования [11], вопрос об ОУМ света по-прежнему вызывает большой интерес у оптического сообщества как в связи с фундаментальными [33], так и с прикладными вопросами [34].

Задача об управлении ОУМ особенно актуальна в свете вопросов о передаче информации на состояниях с ОУМ [12, 14, 17]. В частности, для оптоволоконных линий связи использование волоконных резонаторов различных схем позволяет добиться сверхэффективного управления ТЗ и ОУМ передаваемого оптического сигнала [25, 35 – 37]. Это можно продемонстрировать и для трёхвиткового МКР. С этой целью, учи- тывая параксиальность распространения света в слабонаправляющем волокне, применим выражения для усредненного по времени ОУМ 〈Lz〉 и СУМ 〈Sz〉 в поперечном сечении, отнесенных к усредненной по времени линейной плотности энергии 〈W 〉 в том же поперечном сечении [38]:

_ω L z ₌ Ψ- i ∂ / ∂ϕΨ _≡Ο W ΨΨ

ωSz =Ψσˆ3 Ψ W ΨΨ

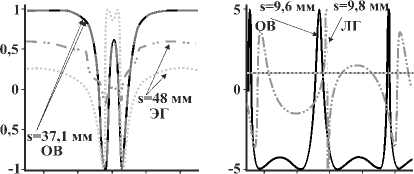
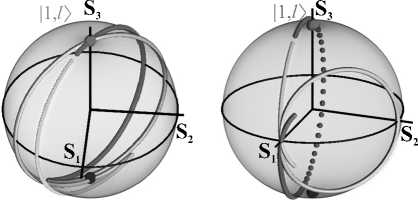
где σˆ 3 – матрица Паули, ω – частота излучения; поля записаны в базисе круговых поляризаций: | V) = col (e+, e-), e± = (ex + iey) / ^2 . На рис. 5а, б приведены графики зависимости ОУМ и СУМ выходящего поля от длины s витка, когда ОЗ возбуждается ОВ, ЭГ-подобными и ЛГ-пучками. Видно, что УМ крайне чувствительны к изменению длины витка, что коррелирует с результатами, приведенными на рис. 3,4. На рис. 5а продемонстрирован отклик СУМ на субволновые вариации длины витка, что является уникальной особенностью для оптических систем. Аналогичная чувствительность имеет место и для ОУМ. Данное свойство трёхвиткового МКР может быть полезным для сверхэффективного параметриче- ского управления как состоянием поляризации, так и ТЗ поля. Заметим, что это, как и в случае двухвитковых МКР, является следствием усиления СОВ [35]. При λ> 1 состояние поляризации выходящего поля остаётся исходным (рис. 5б), так как нормальные моды расцеплены по поляризации. В этом случае эволюцию выходящего структурированного света удобно изобразить на орбитальной сфере Пуанкаре (СП) – математическом объекте, который с момента его раннего появления в сингулярной оптике [39] постоянно обсуждался и модифицировался в соответствии с нуждами её текущих задач. Заметим, что, хотя траектория на СП не проходит непосредственно через её полюса, можно выбрать такие геометрические и ма- териальные параметры резонатора, при которых она максимально приблизится к полюсам.

УМ            УМ

-200 -100 0 100 200        -200 -100 0 100 200

а)                               б)

в)                               г)

ОУМ     СУМ

Рис.5. (а) Приведённый ОУМ (сплошные и точечно-точечно-пунктирные линии) и СУМ (пунктирные и точечные кривые) выходящего поля в зависимости от отклонения Δ s длины витка МКР от значения s=48 мм и s=37,1 мм; на вход подаётся ЭГ-подобный пучок ( 1,1 + 1, - 1 ) / 2 и ОВ | 1, 1〉 соответственно. (б) Те же самые кривые при длинах витка s=9,8 мм и s=9,6 мм при подаче на вход МКР ЛГ-пучка ( 1,5 + 1, - 5 ) / 2 и ОВ | 1, 5〉 соответственно. (в, г) Эволюция состояния выходящего поля на орбитальной СП при возбуждении МКР (в) ОВ | 1, 5〉 и (г) ЛГ-пучком ( 1,5 + 1, - 5 ) / 2 .

Траектории для удобства восприятия раскрашены разными цветами

Вопреки тому, что УМ выходящего поля обладает чувствительностью к изменению длины витка МКР на величину порядка длины волны, при фиксированной длине s как ОУМ, так и СУМ изменяются достаточно медленно при изменении координаты Z поперечного сечения, измеренной вдоль центральной линии МКР. На рис. 6 показаны соответствующие кривые для УМ. Подробное объяснение этого кажущегося парадоксальным явления приведено в [25, 36] – случай МКР с несколькими витками не отличается по сути от описанных ранее. Однако более интересен вопрос о величине УМ. Кроме величин Ο, Σ, можно ввести их аналоги, определяемые как

—w'

Ο=ω

W in

—w'

Σ=ω

S z

W in  ,

где 〈 W in 〉 – линейная плотность энергии на входном торце. Из рис. 6 видно, что, хотя величины Ο , Σ по

модулю всегда меньше своих начальных значений, для их аналогов Ο , Σ это не так. Концентрацию УМ в определенных сечениях можно понять как накопление энергии в тех же сечениях. Действительно, ОЗ, являясь резонатором, обладает свойственным резонаторам интерференционным изменением линейной плотности энергии. График для приведённой линейной плотности энергии I ≡ W / W in показан на рис. 6 а и доказывает неравномерность распределения энергии вдоль ОЗ. Ситуация при возбуждении полей с λ > 1 несколько проще. В этом случае состояние поляризации поля и, следовательно, его СУМ остаются неизменными, что продемонстрировано на рис. 7 б . Этот частный пример показывает, что величина Σ лучше всего подходит для описания и оценки состояния поляризации. Разумеется, аналогичное утверждение справедливо и для Ο .

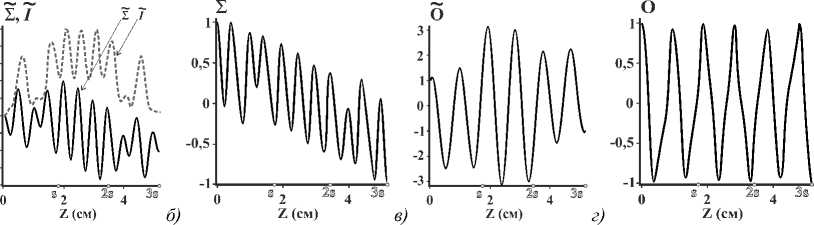
Рис. 6. Величина СУМ Σ, Σ (а,б) и ОУМ Ο, Ο (в,г) в поперечном сечении с координатой Z, измеренной вдоль центральной линии волокна. Точечная линия соответствует I . На вход резонатора подаётся ОВ |1, 1〉; s =17,284 мм. Для удобства на горизонтальной оси отмечены границы витков

Трёхвитковая ОЗ также может служить в качестве основы для квантовых логических вентилей [40]. В противоположность к существующим реализациям некоторых типов логических вентилей для ОУМ, МКР могут быть использованы для создания нескольких типов таких вентилей. Действительно, рассмотрим действие ОЗ на логический ноль | 0〉 (ОВ | 1, l 〉 ) и логическую единицу (ОВ | 1, – l 〉 ). На основе рис. 8 можно сделать вывод, что вблизи области почти полной конверсии логического нуля | 0〉 в логическую единицу | 1〉 (и наоборот) действие ОЗ на входящее поле может быть качественно описано с помощью оператора следующего вида

M = 10 + e ^{i φ} 01, (9)

где φ = φ1– φ2, и φ1, φ2 – фазы выходящих полей |0〉, |1〉 соответственно. Заметим, что выражение (9) записано с точностью до несущественного фазового множителя. Если при некоторой длине волны λ1 выполняется равенство φ =0, то можно говорить, что реализуется логический Х-вентиль. На рис. 8а данное событие отвечает пересечению зелёной точечной кривой φ =0 и точечнопунктирной кривой для φ. Аналогично, если при некоторой длине волны λ2 разница φ 1 – φ2 достигает значения π, реализуется квантовый Y-вентиль. Необходимо отметить, что при длине волны λ1 конверсия логического нуля |0〉 в логическую единицу (и наоборот) равна 98%, а при длине волны λ2 – примерно 95%.

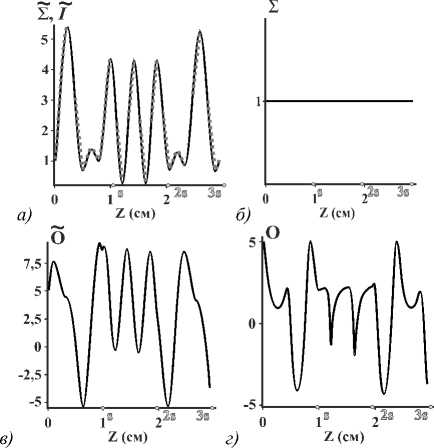
Рис. 7. СУМ (а,б) , ОУМ (в,г) и I (точечная кривая, наложенная сверху кривой для Σ ) в поперечном сечении с координатой Z, измеренной вдоль центральной линии волокна. На вход резонатора подаётся ОВ | 1, 5〉 ; s = 9,8 мм. Для удобства на горизонтальной оси отмечены границы

витков

632,81 A, A, 632,82

а)             X (нм)

---|1,Z>- - |l,-/> — -Ф

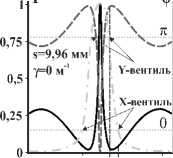
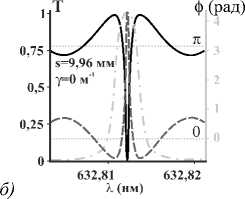
Рис. 8. Реализация логических вентилей на базе 3-витковой ОЗ. Логический ноль | 0〉 – ОВ | 1, l 〉 , логическая единица| 1〉 – ОВ | 1, – l 〉 . Зелёная точечно-пунктирная кривая отвечает разнице фаз между выходящими ОВ | 1, l 〉 и| 1, – l 〉 .

Точки φ = 0 отвечают реализации логического X-вентиля, φ = π – логического Y-вентиля

Заключение

В данной работе мы исследовали преобразование структурированного света и его углового момента в трёхвитковой оптической змее – микрокатушечном резонаторе, состоящем из трёх эванесцентно связанных витков. Изучение проводилось на основе разработанной нами векторной теории нормальных мод с учётом спин-орбитального взаимодействия. Полученные аналитические выражения для нормальных мод и их постоянных распространения позволили изучить прохождение через резонатор оптических вихрей, Эрмит–Гауссово-подобных и Лагерр– Гауссовых пучков. При этом была продемонстрирована возможность сверхэффективного параметрического управления топологическим зарядом, орбитальным и спиновым угловыми моментами выходящего из резонатора поля. Также была показана потенциальная пригодность трёхвитковой оптической змеи для создания на их основе элементов линии задержки и квантовых логических вентилей Паули Х- и Y-типа.

Работа выполнена при поддержке Российского научного фонда (Грант № 20-12-00291)