Трансформация указательных поверхностей упругих свойств текстурированных материалов

Как известно, указательной поверхностью (индикатрисой) называется вспомогательная поверхность, характеризующая зависимость какого-либо свойства среды от направления. Для построения указательной поверхности из одной точки проводят радиус-векторы, длина которых пропорциональна величине, характеризующей данное свойство в данном направлении, например, электропроводность, показатель преломления, модуль упругости. Указательные поверхности служат наглядным графическим представлением об анизотропии физических свойств. Для упругих свойств наряду с указательными поверхностями используются также так называемые направляющие поверхности или поверхности растяжения [1].

Указательные поверхности относятся к центральным поверхностям, и для их построения используется сферическая система координат. Так, указательная поверхность для модуля Юнга ортотропного материала может быть построена с помощью соотношения [2]

E ⁽ n )

6 ( n to ^{( 1} ) n ) _ 6

1 = 1 X 1          l =

( n i n j ® V ) ) x *

,

где E ( n ) - модуль Юнга в направлении n , X * - модули Кельвина - Рыхлевского, характеризующие упругие свойства материала, го ^{( 1}) - компоненты тензорного базиса в пространстве симметричных тензоров второго ранга.

Пусть анизотропный материал представляет поликристаллический агрегат, состоящий из множества произвольным образом ориентированных зерен, имеющих в общем случае некоторую преимущественную ориентацию (кристаллографическую текстуру). В этом случае модули упругости Кельвина – Рыхлевского являются функциями упругих свойств кристаллитов и параметров текстуры.

Для их определения могут быть использованы различные схемы расчета. В частности, используя их вычисление как средние геометрические соответствующих монокри-стальных констант, для поликристаллов с кубической симметрией структуры имеем [3]

x^ = Xp

X* 3 = X2(1-3А1+А2 -Л3 + 2p2,3(л2 -А3 ))X4(зА1-А2 +А3 -2p2,3 (а2 - где модули Кельвина – Рыхлевского кубического кристалла выражаются через модули упругости ( K - объемный модуль упругости) в обозначениях Фойгта равенствами

Вид базисных тензоров в данном случае определяется только текстурными параметрами Л i , i = 1 , 2 , 3 . При этом

1 to( ) = -,=

01

17

2 + 2 p 2,3 + 2 p 2,3

Г1

^p 2 , 3 0

0 1

,

1 - p2,3 )

0 1

,

0 7

1 toV ) = —;=

,

11

0 7

Г0

о 1

.

^Л 1   ^Л 2

^Л 2 ^-Л 3

Очевидно, что один и тот же материал в разных его текстурных состояниях будет иметь в общем случае разную анизотропию упругих свойств, что сопровождается трансформацией указательной поверхности модуля нормальной упругости.

Другой графической характеристикой анизотропии упругих свойств может служить указательная поверхность модуля сдвига G ( И ) при кручении, которая может быть построена с помощью соотношения [4]

2 E-1 (n )+ G-1 (n )= 2 E    G ;,1, где Eиз и Gиз – модули Юнга и сдвига при кручении квазиизотропного поликристалла.

Из этого соотношения следует, что увеличению модуля Юнга в каком-то направлении соответствует уменьшение модуля сдвига при кручении вокруг этого направления.

Построение указательных поверхностей модуля сдвига при простом сдвиге и коэффициента Пуассона также возможно, но требует дополнительных ограничений, поскольку эти упругие характеристики определяются ориентацией двух связанных между собой ортогональных векторов, задающих плоскость и направление сдвига в первом случае, и направления продольной и поперечной деформаций во втором. При этом удобно использовать инвариантное представление технических характеристик упругих свойств [2]. Коэффициент Пуассона v ( m,n ) в направлении fh при растяжении в направлении n определяется из формулы

= E               = E e (n)    i-1         x-           i-1           r;

Модуль сдвига G ( m , n ) при сдвиговой деформации в плоскости, задаваемой вектором m , в направлении n дается равенством

Построение указательных поверхностей с использованием этих соотношений может быть осуществлено несколькими путями, в частности, при построении указательной поверхности коэффициента Пуассона можно зафиксировать положение направления поперечной деформации, изменяя направление оси растяжения в пространстве.

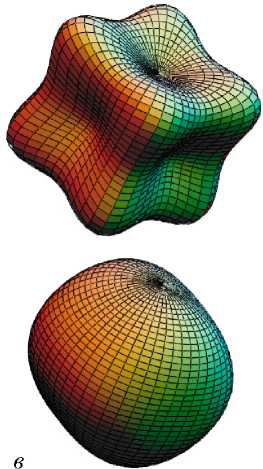
В качестве примера возможной трансформации указательных поверхностей упругих свойств на рис. 1 представлены соответствующие поверхности монокристалла железа A1 = 0, A 2 = 0, A 3 = 0 и текстурированных поликристаллов железа, в зависимости от изменения параметров текстуры. Для примера взяты образцы стального проката [5] следующего химического состава, мас. %: Fe 99,7; Si 0,3, один после холодной прокатки с обжатием 75% , когда A1 = 0,2, A2 = 0,23, A3 = 0,24; другой - после холодной прокатки и отжига при 7000С, когда A1 = 0,17, A 2 = 0,23, A3 = 0,23; и третий образец [6] прокатанного на 92% технически чистого железа, когда A1 = 0,22, A2 = 0,23, A3 = 0,28. В соответствии с принципом Неймана симметрия указательных поверхностей определяется симметрией функции распределения ориентаций кристаллографических осей зерен поликристалла.

а

б

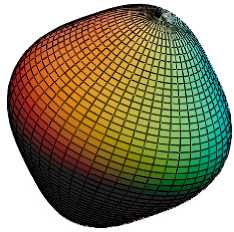
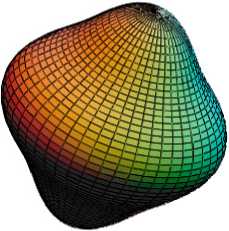
Рис.1. Указательные поверхности модуля нормальной упругости текстурированных поликристаллов железа, в зависимости от изменения параметров текстуры: а – для монокристалла железа

A 1 = 0 , A 2 = 0 , A 3 = 0 ; б - сталь (мас. %: Fe 99,7; Si 0.3) после холодной прокатки с обжатием 75% A 1 = 0,2, A ₂ = 0,23, A ₃ = 0,24 ; в - сталь (мас. %: Fe 99,7; Si 0,3) после холодной прокатки и отжига при 7000С

A1 = 0,17, A2 = 0,23, A3 = 0,23; г - прокатанное на 92% технически чистое железо A1 = 0,22, A2 = 0,23, A3 = 0,28

Функция распределения ориентаций F ( ф , v , 9 ) показывает, во сколько раз совместная плотность распределения углов Эйлера, задающая распределение кристаллографических осей, отличается от таковой для нетекстурированного материала, то есть

f (ф, v, 9) = F (ф, v, 9) ^-sin9.8п

Текстурные параметры могут быть найдены путем непосредственного интегрирования с известной функцией распределения ориентаций, полученной из прямых методов количественного текстурного анализа,

• п 2 п 2 п

• А , = Г2 Ш ( Q 2 Q 22 ⁺ Q 2 Q 3 ⁺ О'Q 2 F < ф , v - ⁶ ) ^{sin 6} d ф d v d 9 , i = 1 , 2 , 3 ,

• ^{8 п} 00 0 0

где Q_i j – косинусы углов между кристаллографическими осями зерен и осями лабораторной системы координат, выражаемые через углы Эйлера.

При моделировании текстуры набором идеальных ориентировок плотность распределения f ( ф , v , 9 ) представляется суперпозицией дельта-функций Дирака и текстурные параметры в этом случае вычисляются по формуле

π 2π 2π                                    n а, =Ш (Q Q2 + Q2Q3 + Q2 Q3 Е Р, $(ф-ф, )5(ф - ф,) 5 (9-9,)dфdvd9, i = 1, 2, 3,

0 0 0                                               I = 1

где p_l – относительная объемная доля текстурной компоненты, задаваемой углами ф i^- v i^{- 9} 1 .

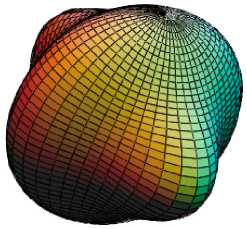
На рис.2 представлена трансформация указательной поверхности модуля нормальной упругости стали Х70 [7], используемой в качестве материала сварного газопровода (труба диаметром 1,5 м с толщиной стенки 16 мм). Текстура листового материала трубы многокомпонентна и неоднородна по сечению. Типы текстурных компонентов и их объемное содержание в разных слоях листов определяются режимами обработки. С учетом объемного содержания компонент текстуры вычисленные текстурные параметры в поверхностных слоях задаются следующими соотношениями: А , = 0,22, А ₂ = 0,23, А 3 = 0,19, а в центральных слоях - А , = 0,31, А ₂ = 0,25, А ₃ = 0,23 .

а

б

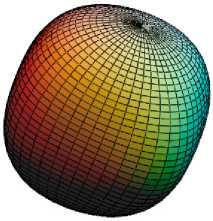
Рис. 2. Указательные поверхности модуля нормальной упругости стали Х70, используемой в качестве материала сварного газопровода (труба диаметром 1.5 м с толщиной стенки 16 мм): а – центральные слои

• А , = 0,31, А ₂ = 0,25, А ₃ = 0,23 ; б - поверхностные слои

А , = 0,22, А ₂ = 0,23, А ₃ = 0,19