Tree-Based Matched RFID Yoking Making It More Practical and Efficient

Published Online October 2009 in MECS

Radio Frequency Identification (RFID), due to low cost and convenience in identifying an object without physical contact, has been deemed to bring a new IT revolution,   and many creative applications are extensively explored   recently. Unlike RFID authentication protocols where an on-line verifier (for example, a reader) that wants to authenticate a tag, RFID yoking proof protocol, first introduced by Juels [1], allows an off-line verifier to collect the evidence of the simultaneous presence of two tags. One typical application scenario of yoking proof is like that: a manufacture of PCs would like to ensure each PC is shipped with its information leaflet; therefore, the manufacture could tag each PC and each leaflet with distinct tags, and then apply the yoking protocol to collect the evidence of the simultaneous presence of the tags (which implies the presence of the products) before the shipment. Please notice that the verifier in an RFID authentication protocol is on-line, while the verifier in an RFID yoking is usually off-line.

Based on the rationale used by an RFID authentication protocol to identify a tag while protecting the anonymity, we may classify such protocols into the following categories, as depicted in Fig. 1 [13]. Note that we only focus on the techniques to identify tags while preserving the anonymity, without covering the details of the protocols. These approaches exhibit different features and computation performance. The yoking schemes are

Manuscript received January 21, 2009; revised June 16, 2009; accepted July 11, 2009.

based on these approaches too, and inherit the same features.

Simple challenge-response approach . In this approach, each tag T_i shares a distinct key k_i with the server or the reader. When a reader R probes a tag T_i by sending a random value N_R as a challenge, the tag T_i responds with h ( k_i , N_R ) , where h () denotes a secure one-way function that can output commitment on its inputs while protecting the un-disclosed input k_i . Upon receiving the response h ( k_i , N_R ) , the server verifies h ( k_j , N_R ) for each potential tag T_j in its database to check whether there is a matched one. This approach allows the server to identify a tag without disclosing the identity to eavesdroppers. Each tag just keeps one secret key, but the server needs to perform the computation for each potential tag to identify the tag. So, the tag’s storage space is O(1) but the computational cost for identifying a tag is O( N ), where N is the number of possible tags. The previous protocols like [14] adopted this approach.

Tree-walk approach . In this approach, the tags are organized as a tree, where each leaf node in the tree denotes one tag and each edge in the tree is associated with a key. Fig. 1(b) shows a simple example. In the example, the tag T 1 holds the key K 1 and K 3, and the tag T 2 holds the keys K 1 and K 4. When a reader probes the tag T 2 by sending a challenge N_R , the tag T 2 responds with { h ( K ₁, N_R ) , h ( K ₄, N_R ) } on which the server can perform the so-called depth-first-search to identify the tag. This approach requires O(log N ) key space on each tag and O(log N ) computational cost for identifying a tag. However, the required key space is a serious burden on low-cost tags. One more serious problem of this approach is that once a tag is compromised, other tags that share the same keys on the same key path could be partially traced. The more the number of keys one tag T_i shares with the compromised tag T_j , the more probability the tag T_i could be identified and traced. The protocols proposed like [9] adopted this approach. We shall adopt tree approach but our scheme would not inherit the shared-compromised path problem the previous schemes have, due to our new tree arrangement.

Hash chains approach. One well-known work of this approach is Ohkubo et al. ’s protocol [15]. In this approach, the server and each tag T _x share a distinct hash seed s _{1 x} initially. For each query request, the tag T x updates s i ₊ i x = h ( s i x ) for i >  1 and responds with a i x = g ( s i x ) , where h () and g () are two different hash functions. This approach achieves the forward secrecy property. That is, if a tag is compromised some day in the future, then the past communications from the same tag can not be traced. However, Ohkubo et al.’s original version cannot resist the replay attack and has the problem of poor scalability [16]. In Ohkubo et al.’s protocol, the computational cost for identifying a tag is O( nm ), where n is the number of potential tags and m is the maximum length of the hash chain. Lately, Avoine et al. [16] proposed an improvement to overcome the replay attack inherent in the Ohkubo et al.’s original version. However, their improvement reduces the time complexity at the cost of extra memory required.

Varying Pseudonym (VP) approach . In this approach, each tag synchronizes its varying identifier and its internal state with the server. The varying identifier is called pseudonym in [17, 18] and is called metaID in [19]. Here, we all refer to them the pseudonyms. Upon receiving a challenge request, a tag responds with the current pseudonym and the commitment on the challenge and the secret internal state. The server verifies the tag based on the commitment. During the authentication stage, the tag and the server respectively update their pseudonyms and their internal state. In this approach, the pseudonym not only protects the anonymity of the tag but also facilitates the server to identify the tag in its database with O(1) computational complexity, because the server can directly use the pseudonym to locate the corresponding entry in its database and perform necessary computations for this matched entry only. Furthermore, each tag only needs constant quantity of internal values, i.e., O(1) key space. These excellent features make the VP-based approach more attractive than the other ones. However, due to the synchronization requirement, the VP-based protocols are prone to the desynchronization attacks (or the Denial-of-Service (DOS) attacks), if an adversary can manipulate the communications to let the tag and the server be out of synchronization. It should be noted that some challengeresponse-based protocols like [9, 20] also synchronize the state between the tags and the server. But these protocols do not send a varying pseudonym to facilitate the server to perform fast identification, and therefore, we do not count them in the VP approach.

From the previous analysis of RFID authentication schemes, we find that tree-based approach can exhibit excellent merits if we can solve the shared-compromised path problem. Therefore, our new yoking scheme will adopt this approach.

Even though there are already quite lots of efforts devoted to explore RFID authentication, most of previous RFID yoking scheme adopted only simple challenge-and-response approach and many of them did not consider anonymity.

While Juels called the protocol the yoking protocol, Saito and Sakurai [6] called it the grouping proof protocol and Lopes et al. [4] called it the clumping protocol. In this paper, we refer to them all as yoking protocols (or proofs).

Following Juels’s work, Saito and Sakurai [6] applied the timestamp to improve Juels’s scheme to resist replay attacks; however, Piramuthu [5] showed that Saito-Sakurai’s scheme failed to resist the replay attack, and proposed an enhanced scheme using random number challenges. Lopes et al. [4] showed the weakness of Piramuthu’s scheme that un-correlated random numbers in the scheme could be exploited to forge valid transcripts.

Furthermore, all the previous yoking protocols like [1-7] did not explicitly specify how a tag should decide whether or not to join a specific yoking session; that is, all the tags (either related or un-related) in a reader’s communication range would join the yoking sessions when the reader probes them, and the verifier should take lots of efforts to filter out un-correlated data off-line .

Usually, there are not only interested tags but also many un-related tags in the reader’s communication range. Applying the previous yoking schemes not only triggers many useless interactions when the reader probes these tags, but also increases un-necessary overhead on the verifier. Only until recently, Burmester et al. [2] introduced the concept of the group identification to explicitly specify which group of tags should join a specific yoking session. This improvement allows the reader to filter out some un-related tags and explicitly link those interested tags together without the verifier’s involvement. However, we observe that (1) Burmester et al. anonymous yoking proofs cannot resist the denial of service attack (DOS attack), and (2) only the inclusion of group identification is not enough to completely filter out un-related (or in-correct) yoking sessions because we have to discriminate the different types of tags of the same group; otherwise, the yoking protocol might only count the number of tags of the same group instead of grouping matched tags of the same group. Take the case of PCs and information leaflets as an example. When a verifier executes the yoking proof protocol, what the evidence he needs is the simultaneous presence of one PC and one information leaflet instead of two PCs or two information leaflets. Without discriminating the distinct types of tags of the same group, Burmester et al.’s protocols would only count the tags (it counts the number of simultaneous-presented tags of the same group) instead of yoking tags of matched types of the same group.

That is, the previous schemes not only trigger many useless interactions but also increase un-necessary overhead on the verifier. Take the case of PCs and information leaflets as an example. When a verifier executes the yoking proof protocol, what the evidence required is the simultaneous presence of one PC with one information leaflet instead of two PCs or two information leaflets. One possible solution is to send out each identity of one possible PC tag with each identity of one possible information-leaflet tag. However, this solution requires the readers to know and send out all possible identities. It is not efficient at all. We, therefore, introduce the matched yoking scheme, where the protocol discriminates the different types of tags and explicitly specifies what types of tags are to be yoked in a yoking session such that only those matched tags should join the session. Our matched yoking proof protocol protects tags’ anonymity such that an adversary cannot identify and cannot track a specific tag using the communication data.

Based on the rationales of existing RFID authentication protocols that preserve tag anonymity, we have classified them into several categories. The first category (or called approach in the following) to authenticate RFID while preserving the anonymity is based on simple challenge-and-response likes that of Weis et al.’s work [8]. The computational complexity of identifying a tag of this approach is linear to N , where N is the number of tags in the system.

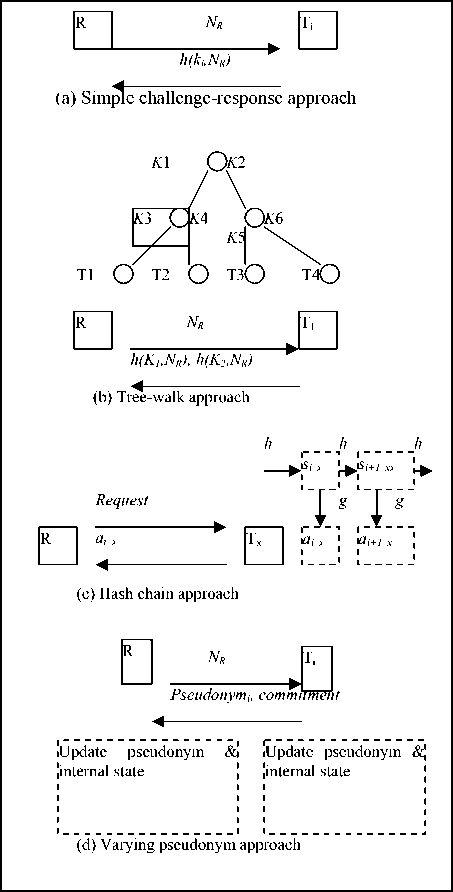
Figure 1. Different approaches to protect RFID tag identity

The above approach is not efficient regarding the computational complexity for identifying a tag; therefore, the tree-based approaches like [9, 10, 11] have been explored to improve the complexity from linear complexity O( N ) to logarithmic complexity O(log N ). In [7], Chien and Liu further improved the computational complexity of tag identification from O( logN ) to O(1).

In this paper, we shall propose a tree-based matched RFID yoking scheme which enhances the cost of identification from O(log N ) to O(1) and allows the reader to collect only those matched tags so that it significantly reduces useless data for the verifier to validate off-line. The rest of this paper is organized as follows. Section 2 discusses the security requirements of matched RFID yoking protocols. Section 3 proposes our tree-based matched yoking-proof scheme. Section 4 analyzes the security and evaluates its performance. Finally, conclusion remarks are given in Section 5.

• II.    SECURITY REQUIREMENTS

The desirable security properties of a secure matched RFID yoking protocol are introduced as follows.

Privacy: Attacker might intercept the transmissions, but she should not acquire any content of the transmissions.

Anonymity and un-traceability: An attacker should not learn the identity or trace a tag from the transmissions.

Dos attack resistance: The adversary might cause tags to assume a state from which they can no longer function properly. Therefore, a secure RFID yoking protocol should provide DOS attack resistance.

Replay attack resistance: A secure protocol should deter an attacker from replaying old messages to break the system.

Matched tag filtering: to eliminate obvious useless data and efforts, a matched yoking scheme should allow readers and tags to collect/join those matched sessions.

Secure binding to specific time span: each yoking proof should be securely bound to a specific time span so that the collected proof proves that the proof really happened within the designed time span.

• III.    THE PROPOSED TREE-BASED YOKING PROOF

In this section, we shall propose a tree-based matched yoking proof scheme.

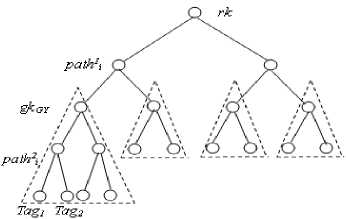
In our scheme, the tags are organized into distinct groups so that only tags belonging to the same group might match each other, and, to further reduce useless data, we assign distinct types to tags of the same group. To implement the concept, we apply hierarchical binary trees to organize tags, where tags of the same group are assigned to the leaves of the same sub-tree, the path from the root to the node of the sub-tree serves as the identity of the group while the path from the sub-tree to the leaf serves as the identity of the tag. Therefore, the identity (the path) of a tag consists of two parts, path¹ and path² , where path¹ s is the identity of the group while path² is the identity of the tag identify the tag of the group. Fig. 2 shows one example of the tree organization of tags, where the triangles with dash lines denote the groups.

Each tag, say Tag i , has its group identity Path¹ i and its distinct tag identity Path² i . Each tag has two keys which are gk_GY , lk_Ti , where gk_GY is the shared group key of the same group, and lk Ti is Tag i ‘s secret key. The three keys are independent. We follow the conventional naming mechanism to name the link and the path. The backend server maintains all the paths and the secret keys of every tag, while the reader only keeps the group level information of each tag; that is Path¹ i and gk GY . This arrangement allows reader to collect proof of tags from the same group and they have matched types.

It is assumed that the verifier is off-line, the channel between the reader and the backend server is secure, and the reader periodically receives authenticated t = EkV (timestamp) from the backend server (the verifier), where t = EkV (timestamp) is an encryption of the verifier’s timestamp using the key kV ( kV is the secret key owned by the verifier). The proofs corresponding to a specific t should be returned within a reasonable time span.

^Ii

Figure2. Tree organization of groups of tags

Before presenting our scheme, we first introduce the notation as follows.

R : The reader.

Tag A : The tag and its identity.

t = E_kV ( timestamp ) : Challenge from the verifier. It is an encryption of the verifier’s timestamp using the key k_V ( k_V is the secret key owned by the verifier).

Path¹ i : The identity of a group; that is the path from the root to the first node of the group.

gk_GY : The key of a group.

TP , TP

• ^{Y 1,    Y 2} : The two type identities of one group.

Path² i : The path from the first node of a group to the leaf node of the tag Tag i .

Lk A : The secret key of a leaf node (Tag A ).

h () : hash function.

N_i : Random number.

Now we are ready to present our yoking proof protocol as follows. Fig. 3 shows the protocol, which consists of two phases. In Phase 1 which is an un-timed phase, the reader broadcasts the group identity, Path¹_i , to invoke those tags from the same group and to check whether two interested tags are of matched types before proceeding to the next phase. In Phase 2 which is a timed phase, reader and tags co-operatively generates the evidence of the simultaneous presence of two tags within the specified time limit. The details are specified as follows.

Round 1:

Step 1. R ^ Tag A and Tag s . : t = E k V ( timestamp ) , Path A

The reader receives the authenticated t from the verifier, and forwards it and the expected group Path ¹ _A ( = Path ¹ _B ) to Tag A and Tag B .

Step 2.a . Tag A ^ R : al, TPy 1

Step 2.b : Tag B . ^ R : bl, TPy 2

Upon receiving the challenge t and the expected group Path1A(= Path1B) , TagA and TagB respectively check whether they belong to the same group. If so, TagA computes al = h(gkGY,t,TPY 1) and responds al and its type identity TPY1 to the reader; likewise, TagB computes bl = h(gkGY,t,TP2) and responds bl and its type identity TPY2 to the reader.

The reader checks the validity of a1 and b1 , and checks whether the two types are matched. If the verification satisfies, it proceeds to the next round and steps; otherwise, it terminates this instance.

Round 2.

Step 3.a: R ^ Tag A : b l, TPy 2

Step 3.b: R . ^ Tag B : a l, TPy 1

The reader respectively forwards Tag A ‘s and Tag B ’s responses to the other tag so that they can check whether they are matched tags proceeds to the next step. Step 4 . Tag A ^ R : n A , a 2, a 3

When Tag A has verified it matches with Tag B , it chooses a random nonce n_A , computes a 2 = h ( gk GY , t ) ® Path A and a 3 = h ( b 1, t , TPy 1 , Ik A ) , and sends n_A , a 2 and a 3 to R, which forwards a 2 and n_A to Tag B .

Step 5 . R ^ Tag B : a 2, n A

Step 6 . Tag B ^ R : b2 , b3

Tag B encodes its identity in the form b 2 = h ( gk GY , t ) ® Path B , computes b 3 = h ( n A , a 3, TY_{Y 2}, lk_B ) , and sends b2 , b3 to R , which forwards to Tag A .

Step 6 . Tag A ^ R : a4

Tag A computes a 4 = h ( b 3, Ik A ).

The final evidence     P_AB    consists of

{ t , Path ¹ _A , TP_{Y 1} , TP_{Y 2}, n_A , a 1, a 2, a 3, a 4, b 1, b 2, b 3 } from which the verifier later can verify whether they are matched and the simultaneous presence of the two tags Tag A and Tag B .

• IV.    SECURITY ANALYIS and PERFORMANCE EVALUATION

Security analysis is given as follows.

• •    Anonymity

Tag’s ID of our protocol is not delivered in plaintext but encrypted in the form h(gk_GY, t) Ф Path²_T A . Therefore, the privacy of the identity is ensured. Of course, we should notice that if one tag of the same group is compromised, then the privacy of the identities from the same group would be compromised.

• •    Traceability and Replay attack

The encrypted identity h(gk_GY, t) Ф Path² A in each session depends on the random number t . The encrypted identities of different sessions are random and independent. The attacker, therefore, cannot trace the tags, and replaying old messages cannot cheat the tags, the readers, and the verifier.

• •    Forward secrecy

However, the version does not provide forward secrecy. That is, the past communications from a tag could be identified if the tag were compromised some day later. It might be easy to achieve forward secrecy when we only consider RFID authentication protocols like [3]. However, it is a very challenge to design RFID yoking protocol with forward secrecy because (1) the verifiers in yoking protocols are off-line instead of online in the authentication case, and (2) the states synchronization in yoking protocols involve more than just one tag and its server but several tags of the same group with the server.

• •    Secure binding to the designated time span

Each time the reader to probe tags and collect proofs, it should first receive authenticated encrypted time of the form t = E_k V ( timestamp ) , and the corresponding proof should be returned to the verifier within a reasonable time window. Only the verifier can generate valid encrypted time stamps; therefore, each verified proof proves its secure binding to the designated time.

Table 1. Security properties of related works

	[1]	[6]	[2]	Our protocol
Match checking & prefiltering	X	X	X	O
Anonymity	△	△	O	O
Replay attack	X	X	O	O
Forward secrecy	△	△	O	△
DOS			△

O:satisfy; X :not satisfy; △ : not considered; \: not applicable.

Table 2. Performance evaluation of related works

	[1]	[6]	[2]	Our protocol
The number of steps.	6	5	9	10
Number of hashing operation.	1	1	6	Tag A :5 Tag B :4
The number of random number per tag.	1	1	0	1
The storage of tag.	2	3	6	5
Cost of computing of back-end server.	O( N )	O( N )	O( m )	O(1)

• Performance

We summarize the security performance in Table 1. From Table 1, we can see that our proposed protocol owns the strongest security properties, but we did not consider the forward secrecy property.

Table 2 summarizes the computational performance and the communication performance. We can see that our scheme improves the security weaknesses of the previous schemes, but it pays the cost of more computations and more communications.

• V.    CONCLUSION

This paper has proposed a tree-based matched RFID yoking scheme which enhances the cost of identification from O(log N ) to O(1), where N is the number of tags, and allows the reader to collect only those matched tags such that it significantly reduces useless data for the verifier to validate off-line. These features make the yoking scheme much more practical and efficient.