Трех- и четырехуровневые спиральные фазовые пластинки

В последнее время возрос интерес исследователей к оптическим вихрям (optical vortices). Оптический вихрь (ОВ) – это когерентное световое поле, в поперечном сечении которого имеется изолированный ноль (или несколько нулей) интенсивности, а фаза при обходе такой нулевой точки приобретает набег, кратный 2п. Появилось много работ, исследующих распространение оптических вихрей – солитонов в нелинейных средах [1-4]. В [1] численно исследуются ОВ – солитоны, формирующиеся в нелинейной среде лазерного резонатора. Сингулярные пучки – эллиптиконы, которые описываются функциями Айнса-Гаусса и которые могут быть сформированы в нелокальной нелинейной среде, исследуются в [2]. В [3] экспериментально изучались ОВ с радиальной и азимутальной поляризациями, которые формируются в самофокусирующей среде с керровской нелинейностью. Оптические вихри могут быть сформированы также сложением нескольких волн в нелинейной среде, внутри которой синтезирован спиральный фотонный кристалл [4]. В [5] описывается золотое зеркало – голограмма, которое изготавливалось по технологии лазерного травления с помощью фемтосекундного сапфирового лазера с длинной волны 800 нм и которое использовалось для формирования ОВ из фемтосекундных мощных лазерных импульсов. В [6, 7] с помощью лазерных интерферометров исследовались фазовое распределение [6] и угловой орбитальный момент [7] ОВ, порожденных пучком Лагерра – Гаусса (ЛГ). В [8, 9] описываются новые семейства лазерных пучков, обладающих цилиндрической симметрией и несущих угловой орбитальный момент: круговые частичные пучки [8] и гипергеометрические лазерные пучки [9]. Эти лазерные пучки также являются примерами ОВ. В [10] численно показано, что ОВ, сформированный лазерной модой ЛГ, распространяясь в турбулентной атмосфере (турбулентность выбиралась Колмогоровского типа), сохраняет свой топологический заряд на большом расстоянии: на расстоянии 4 км, если топологический заряд n = 1 и на 2 км, если n = 5 . В [11] описана субапертурная адаптивная оптическая система, которая предназначена для на- блюдения объектов через турбулентную атмосферу. Каждая субапертура используется для локальной компенсации искажений волнового фронта. Если вместо приемной субапертуры использовать адаптивное зеркало, вносящее локальную фазовую задержку, то можно с помощью небольшого числа субапертурных адаптивных зеркал сформировать ОВ, и передавать с его помощью информацию через турбулентную атмосферу. В [12] исследуются световые поля, сформированные несколькими, разнесенными в пространстве ОВ, каждый из которых создается модой ЛГ. В [13, 14] рассматривалась многоуровневая спиральная фазовая пластинка (СФП), с помощью которой также можно формировать ОВ. Многоуровневая СФП в [14] имела апертуру в виде правильного многоугольника, и было показано, что при любом числе стороно многоугольника вблизи оптической оси будет формироваться ОВ с фазовой сингулярностью (или дислокацией волнового фронта).

В этой работе, продолжая [14], мы на конкретных примерах покажем, как с помощью всего трех-или четырехуровневых СФП, ограниченных правильными треугольником или четырехугольником, можно сформировать ОВ с топологическим зарядом n = 1,2,4 . Кроме того, мы покажем, что ОВ с n = 1 можно сформировать также с помощью трех круглых субапертур, вносящих фазовые задержки 0 , 2 л/ 3 и 4 П 3 . С помощью таких простых оптических элементов, совмещенных с динамическими адаптивными устройствами [11], можно передавать информацию на большое расстояние, даже в присутствии атмосферной турбулентности [10].

• 2.    Малоуровневые СФП

  • 2.1    Треугольная СФП с тремя уровнями фазы

На рис.1 а схематично показана многоуровневая СПФ с аппретурой в виде правильного многоугольника. В [14] приведена формула (уравнение (2) в [14]), которая выражает комплексную амплитуду в плоскости Фурье-спектра как сумму 3 P слагаемых, каждое из которых связано с одной из сторон равных треугольников, на которые разделена вся апертура многоуровневой СФП, ограниченной правильным P -угольником.

Рис.1 Схема многоуровневой СФП с полиномиальной апертурой (а), интенсивность (б) и фаза (в) картины дифракции Фраунгофера для непрерывной СФП с топологическим зарядом n=6

Приведем здесь эту формулу для удобства:

к if cos p p-1         exp (i T )

E(p'e> - тут 2           ----

2 п k p p - o sin ( p - 9 ) cos a p cos a p + 1

,

„ • п . (        \                  ( . kRp i                ( . kRp x 2sin p sin (pp - 9) + cos ap+1 exp I - i—p cos ap I-cos ap exp I - i—p cos ap+1

п где Tp - npp, Pp -(2п(P) p, p - 0, P -1, ap - Pp - p - 9, p > 3.

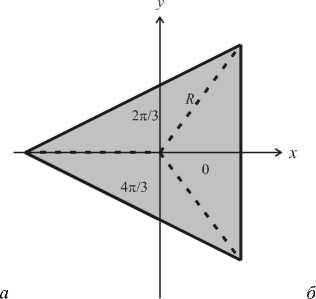
На рисунках 1б и 1в для примера показаны интенсивность и фаза картины дифракции Фраунгофера плоской волны на непрерывной СФП (когда P в (1) стремится к бесконечности) с топологическим зарядом n - 6 . Далее мы будем рассматривать СФП с малым числом уровней фазы и ограниченные диафрагмами в виде многоугольников. На рис. 2а показан вид СФП, ограниченной правильным треугольником, площадь которого раз- делена на три равных треугольника с постоянными фазами 0, 2п/3 и 4^3 • Правильный треугольник можно вписать в окружность радиуса R . Тогда три вершины треугольника будут иметь полярные координаты (R, - П 3), (R, П 3) и (R, п). При P - 3 для СФП с номером n =1 из формулы (1) можно получить:

E (p,9)-

iV3 ) f exp (10) 8п I kp' _

ikRp    , и exp —— cos (п 3 - 9)

+

cos (п + 9) cos (П 3 - 9) cos (п/ 3 + 9)

exp - ^{ikR p} cos ( п 3 + 9 )

+

exp

ikR p

f cos (п + 9)

cos (п + 9) sin (9 - П 3) sin (П 3 + 9)

+

cos (п 3 - 9) sin (п + 9) sin (^ 3 + 9) cos (^ 3 + 9) sin (п + 9) sin (9 - п( 3)

,

где (p, 9) - полярные координаты Фурье-плоскости, k - волновое число света, f - фокусное расстояние сферической Фурье-линзы. Из уравнения (2) следует, что при p ^ 0 вблизи оптической оси сформи- руется ОВ:

E 1 ( p ^ 0, 9 ) «

Г - 3У3 k ² R³ | 48^ f²

p exp ( i 9 ) .

Выражение (3) можно также получить из уравнения (3) в [14], положив P =3 и n =1.

На рис. 2б показана рассчитанная интенсивность 11 (p, 9)- |E1 (p,9)|2 в плоскости Фурье- спектра при дифракции плоской волны на СФП, показанной на рис. 2а. На рис. 2в показана соответствующая фаза светового поля в Фурье-плоскости. Параметры расчета: длина волны X - 633 нм, R - 2 мм, f -150 мм, число отсчетов 512×512. Из рис. 2б, 2в видно, что в центре картины дифракции (на оптической оси) имеется изолированный ноль интенсивности, фаза вблизи которого носит спиральный характер. Также видно, что ОВ имеет площадь, примерно равную диску Эйри с диаметром 1,22λf/R (пунктирная окружность на рис. 2в).

в

Рис. 2 Дифракция Фраунгофера плоской волны на трехуровневой СФП с треугольной апертурой, разделенной на треугольные субапертуры: фаза ДОЭ (а), интенсивность (б) и фаза (в) света в Фурье-плоскости (пунктиром показан диск Эйри)

2.2 Квадратная СФП с четырьмя уровнями фазы

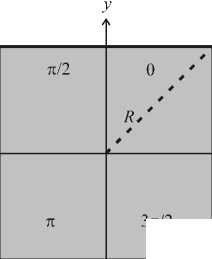
На рис. 3 а показана СФП ( n = 1), ограниченная квадратной апертурой, площадь которой разделена на четыре квадратные равные субапертуры с фазами 0 , л) 2, П и 3 П 2 . Комплексная амплитуда света в плоскости Фурье-спектра при дифракции плоской волны на СФП (рис. 3 а ) имеет вид:

Г — k ² a ³ Y

E2 (f ^ 0, n > 0 )*|      2 |(1-i )(f + in),      (5)

12nf )

или в полярных координатах:

E2 (p ^ 0,9)«

— k ² R ³ ( 1 — i ) 442 n f ²

p exp ( i 9 ) ,

E2 (f, n) =

-ka2 । .   Г kaf ) .   Г kan I

Sine Sine X

П J I 2 f J   I 2 f J

I • ka , _x ■ ■ ka ,        \ I

X1sin —(f + П) — i sin — (f — n) ^,

I L2 f J L2 f        JI

ka

L 2 f

где sine ( x ) = sin ( x )/ x , ( f , n ) - декартовы координаты в Фурье-плоскости, 2 a - сторона квадратной апертуры: R = a42 , R - радиус окружности, в которую вписан квадрат. При f ^ 0 и n ^ 0 вблизи оптической оси сформируется ОВ и комплексная амплитуда будет пропорциональна выражению:

где f = p cos 9 , n = P sin 9 .

Кроме изолированного нуля интенсивности в центре картины дифракции имеется множество изолированных нулей, вблизи которых фаза имеет сингулярный (винтовой) характер.

Например, при f = ± n в точках f _n = X fn, ( 2 a ) , где n = 1,2,3,.... На рис. 3 б показана интенсивность картины дифракции Фраунгофера плоской волны на СФП (рис. 3 а ), а на рис. 3 в - фаза картины дифракции. Параметры расчета те же, что и для рис. 2. Несмотря на то, что картина дифракции не обладает круговой симметрией, вблизи ее центра имеется малая область (примерно равная диску Эйри), в которой интенсивность близка к кольцу, а фаза линейно зависит от полярного угла.

а

Зл/2

б

в

Рис. 3 Дифракция Фраунгофера плоской волны на четырехуровневой СФП с квадратной апертурой, разделенной на квадратные субапертуры: фаза ДОЭ (а), интенсивность (б) и фаза (в) света в Фурье-плоскости (пунктиром показан диск Эйри)

На рис. 4 а показан другой возможный вариант разделения квадратной апертуры четырехуровневой СФП ( n = 1) на четыре одинаковых треугольника с

фазами 0 , П 2, п и 3 П 2 . Комплексная амплитуда света в плоскости Фурье-спектра при дифракции плоской волны на СФП (рис. 4 а ) имеет вид:

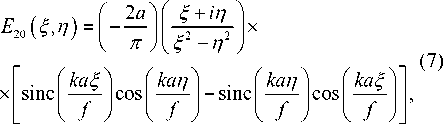
E20 (р ^ 0,9)«

к ² R³ )

4^ n f ² J

p exp ( i 9 ) .

где R = алТ2 . Вблизи оптической оси ( £ ^ 0 , П ^ 0) сформируется ОВ и комплексная амплитуда (7) будет пропорциональна выражению:

На рис. 4 показаны рассчитанные интенсивность (б) и фаза (в) картины дифракции Фраунгофера от четырехуровневой СФП (рис. 4 а ). Видно, что в центре картины дифракции в области, примерно равной диску Эйри с диаметрм 1.22 Х f /R имеет место ОВ с

топологическим зарядом 1.

\    о л/2       '.	R»' / Зл/2
	К      X

a

б

Рис. 4 Дифракция Фраунгофера плоской волны на четырехуровневой СФП с квадратной апертурой, разделенной на треугольные субапертуры: фаза ДОЭ (а), интенсивность (б) и фаза (в) света в Фурье-плоскости (пунктиром показан диск Эйри)

• 2.3 Составная СФП из трех- и четырехуровневых СФП

Так как рассмотренные ранее малоуровневые СФП имеют апертуру в виде правильного треугольника и квадрата, то с помощью них можно формировать сложные (составные) СФП, присоединяя одну ячейку к другой как в домино. Известно, что с помощью правильных 3-х, 4-х и 6-тиугольников можно без пропусков и наложений заполнить всю плоскость.

В качестве примера на рис. 5 показаны: составная СФП (а), которая получается при объединении четырех квадратных СФП (рис. 4 а ), повернутых одна относительно другой на п /2 по часовой стрелке; интенсивность (б) и фаза (в) картины дифракции Фраунгофера плоской волны на трехуровневой СФП (рис. 5 а ). Параметры расчета те же, что и на рис. 2 и 3. Из рис. 5 видно, что в центре картины дифракции сформировался ОВ с топологическим зарядом n = 2.

а

♦Д'

' ' Зл/2 , ' ' к '>'   0 , * л/2 '»	\ 0 / Зл/2       л/2
' л       * л/2 '/ Зл/2 / 0  \	' ч л/2    , * 0 \' л / ЗиЛ \

б

Рис. 5 Четырехуровневая составная СФП (а), состоящая из четырех повернутых относительно друг друга на п/ 2 СФП (рис. 4а); интенсивность (б) и фаза (в) Фурье-спектра

На рис. 6а показана трехуровневая составная СФП, полученная путем объединения шести одинаковых треугольных трехуровневых СФП (рис. 2а) с номерами n = 1. При таком объединении все СФП оказались повернутыми друг относительно друга на л]3 • На рис. 6б и 6в показаны интенсивность и фаза картины дифракции Фраунгофера при дифракции плоской волны на трехуровневой СФП (рис. 6а). Из рис. 6 видно, что в центре картины дифракции (на оптической оси) сформировался ОВ с топологическим зарядом n = 2. Хотя вблизи составной СФП (рис. 6а) образуется ОВ с топологическим зарядом n = 4, в дальней зоне картину дифракции в центре формируют периферийные участки СФП, а как видно из рис. 6а совокупность треугольников, прилежащих к границе апертуры СФП, обладает топологическим зарядом n = 2 .

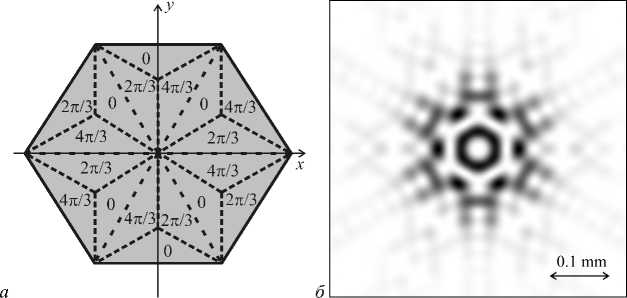
Рис. 6 Трехуровневая составная СФП (а), состоящая из шести треугольных СФП (рис. 2а); интенсивность (б) и фаза (в) в плоскости Фурье-спектра, при дифракции плоской волны на составной трехуровневой СФП (а) (пунктиром показано светлое кольцо картины дифракции)

в

На рис. 7 а показана такая же составная СФП, но с исключенными внешними областями.

На картине дифракции (рис. 7 б ) кольцо получается с разрывами, однако при обходе вдоль него фаза меняется на 8 п (рис. 7 в, область кольца показана пунктирной линией), что соответствует топологическому заряду n = 4 (хотя в центральной части фаза соответствует СФП с n = 2).

• 3.    Трехуровневая СФП, состоящая из трех субапертур

ОВ вблизи оптической оси можно сформировать с помощью СФП, состоящей из трех субапертур с постоянными фазами 0 , 2 п /3 и П 3 .На рис. 8 а показана трехуровневая СФП ( n = 1), апертура которой состоит из трех круглых субапертур радиуса R ₀.

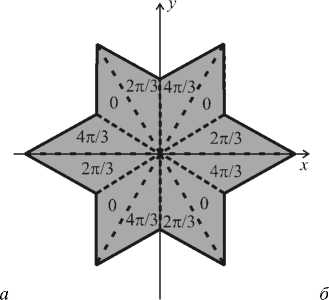
Рис. 7 Трехуровневая составная СФП (а), состоящая из шести треугольных СФП, как на рис. 6а, но с исключенными внешними областями; интенсивность (б) и фаза (в) в плоскости Фурье-спектра (пунктиром показано светлое кольцо картины дифракции, при обходе которого фаза меняется на 8 п )

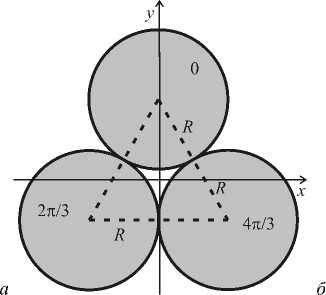
Рис. 8 Трехуровневая трехсубапертурная СФП (а); интенсивность (б) и фаза (в) в плоскости Фурье-спектра

Центры трех кругов являются вершинами правильного треугольника со стороной 2 R ₀ .

Комплексная амплитуда света в плоскости Фурье-спектра, которая описывает дифракцию плоской волны на СФП (рис. 8 а ), имеет вид:

I R I I kRрE3 (р, 9 ) = 2п| — IJ1| ——

I Р ) I f

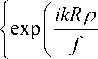
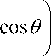
i 2 п ikR p

+ exp---cos

3 f i4п ikRp    f п „

+ exp ---+--cos — + 9

3 f     1 6

+

,

где R = 2 R ₀ /V3 - радиус окружности, в которую вписан треугольник, образованный центрами трех окружностей (рис. 8 а ).

Вблизи центра картины дифракции ( р ^ 0 ) комплексная амплитуда (9) будет пропорциональна выражению, описывающему ОВ с топологическим зарядом n = 1:

E3 ( р ^ 0,9 )®f i3^ Ifk-RR-1 pexp ( i9 ) .      (10)V 8 )< J )

На рис. 8 б и 8 в показаны рассчитанные интенсивность и фаза в плоскости Фурье-спектра, которые формируются при дифракции плоской волны на СФП (рис. 8 а ). Из рис. 8 видно, что вблизи оптической оси в круге диаметром, близким к диаметру диска Эйри, формируется ОВ с n = 1.

• 4.    Заключение

Рассмотрены трех- и четырехуровневые СФП с апертурами в форме треугольника или квадрата, а также трехуровневая СФП, состоящая из трех круглых субапертур. Для описания дифракции Фраунгофера плоских волн на таких простых ДОЭ получены аналитические выражения. Численно показано, что вблизи оптической оси или в центре картины дифракции Фраунгофера в области, примерно равной диску Эйри, формируется оптический вихрь с топологическим зарядом 1. Также численно показано, что составные СФП, набранные из 6 или 4 таких трех- и четырехуровневых СФП, могут формировать оптические вихри с топологическим зарядом 2 и 4.

Работа выполнена при финансовой поддержке Российско-Американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06), и грантов РФФИ 0807-99007 и 07-07-97600.