Трехкомпонентные аэродинамические тензовесы

Воздействие потока на модели, исследуемые в аэродинамических трубах, сводится к силам, непрерывно распределенным по обтекаемой поверхности модели. Эти силы характеризуются в каждой точке поверхности давлением и касательным напряжением. Интегрируя эти нагрузки по поверхности, можно найти суммарные аэродинамические характеристики. Более точным и надежным методом определения суммарных аэродинамических сил и моментов является непосредственный метод измерения сил и моментов при помощи аэродинамических весов. Задачи комплексной автоматизации многофакторного эксперимента не могут быть решены традиционными измерительными системами с преобразователями механического типа. Для решения задач измерений при аэродинамических испытаниях и повышения уровня их автоматизации необходимо использовать тензометрические измерительные системы [1–4].

Одним из основных признаков аэродинамических весов является число измеряемых компонент. В зависимости от этого числа весы могут быть трех-, четырех- и шестикомпонентными.

Шестикомпонентные весы измеряют величины (компоненты) проекций полной аэродинамической силы на выбранные три взаимно перпендикулярные оси координат и три компоненты полного момента относительно этих осей [5–8].

Трехкомпонентные аэродинамические весы измеряют две компоненты полной аэродинамической силы (подъемную силу Y и силу лобового сопротивления Х ) и продольный момент относительно поперечной оси (момент тангажа М z ) [9].

В зависимости от расположения аэродинамических весов относительно модели и аэродинамической трубы они разделяются на два типа: весы, располагаемые вне модели и рабочей части трубы, и весы, располагаемые внутри модели или державки.

Конструкция и принцип работы устройства

В аэродинамической лаборатории кафедры летательных аппаратов разработаны трехкомпонентные весы первого типа.

Работа весов основана на тензометрическом методе измерения сил и моментов. Силовые упругие элементы (балки) конструктивно выполняются так, что они имеют наименьшую жесткость относительно одной из осей. При приложении нагрузки вдоль этой оси возникает наибольшая деформация этого элемента. В других направлениях жесткость упругого элемента значительно больше, и если действуют усилия в направлении других осей, то деформация упругого элемента практически отсутствует. Балки имеют настолько малые деформаџии, что вызванными ими перемещениями модели можно пренебречь. Измерение малых деформаций упругих элементов производится с помощью тензодатчиков, преобразующих величину деформации в изменение электрического сопротивления, которое затем измеряется прибором, соединенным с соответствующей измерительной схемой.

Выбор тензодатчиков в качестве весовых элементов обусловлен их весьма малыми размерами и весом, возможностью измерения очень незначительных относительных деформаций упругих элементов, малой инертностью, что позволяет измерять не только статические, но и динамические нагрузки, а также возможностью дистанционных измерений [10–12].

Напряженное состояние на поверхности упругого элемента, к которой приклеен датчик, может изменяться от точки к точке, поэтому изменение сопротивления датчика пропорционально некоторому среднему напряжению на участке с длиной, равной базе датчика. Для того чтобы датчики фиксировали напряжение в точке, в аэродинамических весах использованы датчики с малой базой (7 мм) сопротивлением 200 Ом. Тензодатчики соединены по мостовой схеме и включены во все четыре плеча моста, что позволяет существенно повысить чувствительность и обеспечить большую точность измерений.

В аэродинамических весах, располагаемых вне модели, разложение полной аэродинамической силы и момента на компоненты осуществляется при помощи упругих звеньев, которые одновременно выполняют роль и измерительных элементов. Конструктивная схема весов представлена на рис. 1.

Модель устанавливается в потоке при помощи хвостовой Г-образной державки, чтобы исключить влияние на поток в том месте рабочей части, где установлена модель. При продувке в аэродинамической трубе измеряется сумма двух аэродинамических сил, одна из которых действует на модель, а другая – на поддерживающие эту модель устройства, размещенные в потоке. Для нахождения силы, действующей только на модель, из суммарного усилия вычитается составляющая, приходящаяся на поддерживающие устройства. Эта составляющая определяется в результате продувки поддерживающих устройств без модели.

Сила лобового сопротивления Х , подъемная сила Y и момент тангажа М_z даются в поточной системе координат, когда ось OX направлена по потоку, ось OY – перпендикулярно ей вверх. За начало координат принят центр давления модели.

V ∞

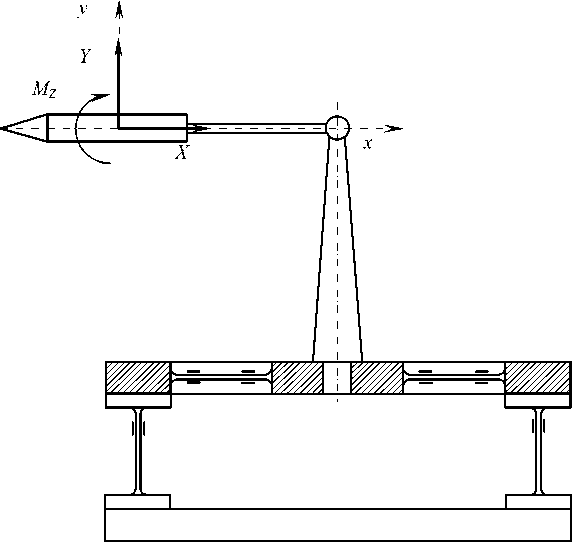
Рис. 1. Конструктивная схема аэродинамических тензовесов

Fig. 1. Design diagram of aerodynamic strain gauges

а

б

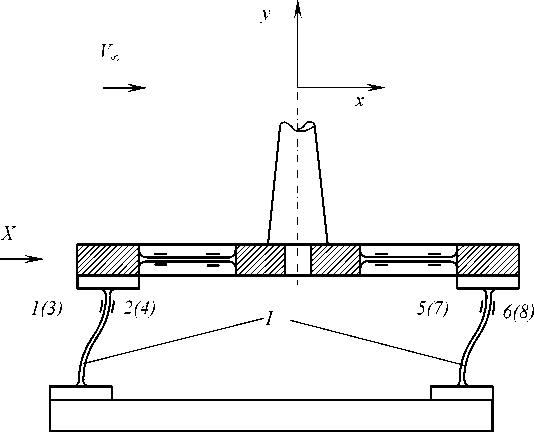
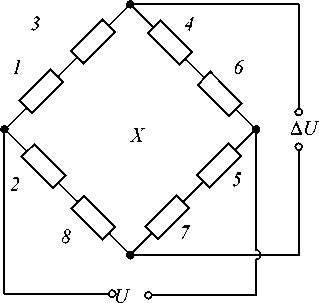
Рис. 2. Измерение силы лобового сопротивления: а – схема деформации измерительных элементов; б – электрическая схема соединения тензодатчиков

Fig. 2. Measurement of drag force: a – deformation diagram of measuring elements; b – electrical connection diagram of load cells

Сила лобового сопротивления Х , действующая на модель, передается через стойку весов на четыре вертикальные балки I (на рис. 2, а показаны только две из них). Упругие элементы имеют очень малое сопротивление изгибу в плоскости действия силы Х и значительную жесткость в перпендикулярной плоскости. Эта составляющая ( Х ) вызывает S-образный изгиб балок (рис. 2, а ). Датчики, наклеенные на противоположные стороны балок, включаются в смежные плечи моста (рис. 2, б ), и мост реагирует лишь на силу сопротивления Х . Другие компоненты ( Y , М z ) являются источниками растяжения или сжатия и не вызывают разбаланса моста.

Для измерения подъемной силы Y и момента тангажа M_z служит горизонтальная балка II с закрепленной на ней державкой.

Под действием подъемной силы Y происходит S-образный изгиб упругих элементов этой балки (рис. 3). Для того чтобы получить выходные сигналы, пропорциональные только этой составляющей, в измерительный мост включены тензодатчики 9–12 , установленные на нижней и верхней поверхностях чувствительных пластин в центральной части балки II . Схема включения датчиков в мост представлена на рис. 3, б . Датчики 9 , 11 и 10 , 12 включены в разные плечи моста. Если на упругие элементы балки II действует подъемная сила, то эти датчики регистрируют деформации разных знаков и на выходе моста появляется сигнал.

Момент тангажа М_z воспринимается упругими элементами, расположенными вдоль оси ОХ (рис. 4, а , б ). На периферийной части чувствительных пластин балки II установлены тензодатчики 13–16 , включенные в измерительный мост, реагирующий на деформацию изгиба упругих элементов только под действием момента тангажа. Деформация горизонтальной балки II вызывает изменение сопротивления не только в тензодатчиках, измеряющих этот момент, но и в тензодатчиках 9 , 11 и 10 , 12 , предназначенных для измерения подъемной силы. Таким образом, имеется определенное влияние момента тангажа на величину измеряемой подъемной силы.

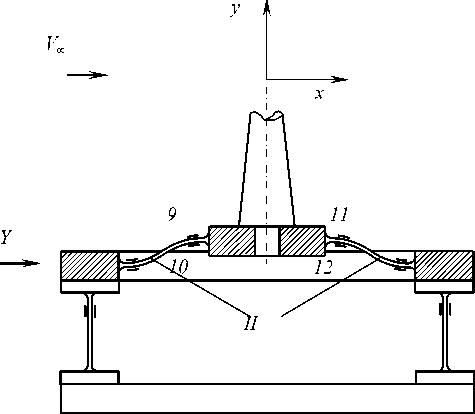
Рис. 3. Измерение подъемной силы: а – схема деформации измерительных элементов; б – электрическая схема соединения тензодатчиков

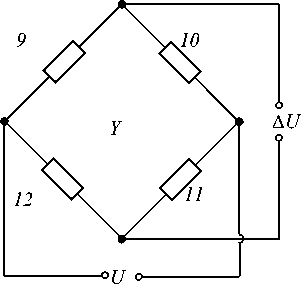
б

Fig. 3. Measurement of lifting force: a – diagram of deformation of measuring elements; b – electrical diagram of connection of load cells

При деформации балки II под действием только подъемной силы изменения сопротивления в тензодатчиках 13–16 , предназначенных для измерения момента тангажа, не наблюдается. Поэтому влияние подъемной силы на момент тангажа отсутствует.

Так как конструкция весов не позволяет электрически разделить компоненты Y и М_z , то влияние момента тангажа на величину подъемной силы определяется в процессе тарировки и оценивается с помощью специального графика влияния, построенного по результатам тари-ровочных данных.

При тензометрических измерениях выходные величины сил и момента, действующие на испытуемую модель, получаются в виде соответствующих показаний прибора, измеряющего электрические сигналы, пропорциональные приложенным силам. Для перевода приборных данных в величины сил и моментов необходимо производитъ совместно тарировку весов и приборов с цељю получения так называемых тарировочных коэффициентов k_x , k_y , k_mz .

Тарировочные коэффициенты представляют собой цену одного деления шкалы прибора в ньютонах при измерении сил или в ньютонометрах при измерении момента. Умножая полученные в эксперименте данные на соответствующий тарировочный коэффициент с учетом влияния поддерживающих устройств, получают величины сил в ньютонах и моментов в ньютонометрах. При этом дополнительные составляющие аэродинамических сил и моментов, создаваемые державкой и определяемые путем её продувки в присутствии модели, вычитаются со своими знаками из приборных данных [13–15].

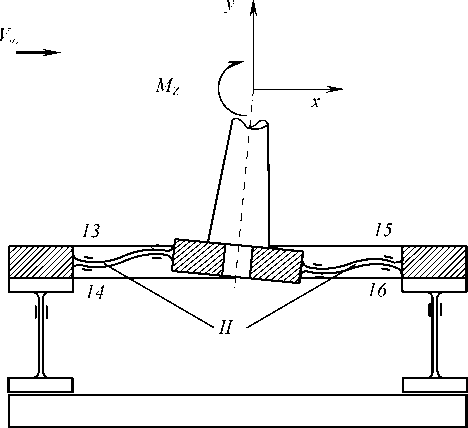
Рис. 4. Измерение момента тангажа: а – схема деформации измерительных элементов; б – электрическая схема соединения тензодатчиков

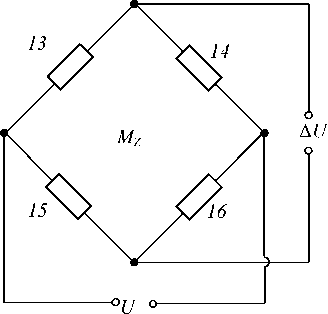
б

Fig. 4. Pitch moment measurement: a – diagram of the deformation of the measuring elements; b – electrical diagram for connecting strain gauges

Величины сил, действующих на модель, могут быть представлены в виде

X мод

X .-X приб держ ^,

7 =Y .-Y -XY, . мод приб держ      Mz, где Xприб, Yприб – показания приборов при продувке системы модель – державка в целом; Xдерж, Yдерж – показания приборов при продувке одной державки; ΔYMz – величина влияния момента тангажа на подъемную силу, определяемая по графику влияния.

Величина момента тангажа, действующего на модель, может быть определена по формуле

M zмод

M z приб   M z держ *

Зная тарировочные коэффициенты k x , k y , k mz , компоненты действующих на модель аэродинамических сил и момента можно вычислитъ по формулам

^X [ H ] = k x ’ ^X мод , ^[ H ] = ^ky ’ ^ мод , ^M [ Нм ] =’ ^km ’ ^Mz мод -

Для определения аэродинамических коэффициентов сил необходимо размерные величины Х [Н] , Y [H] отнести к скоростному напору q ∞ и характерной площади модели S м .

Коэффициент сопротивления определится следующим образом:

₌_X HL₌_ X HL₌— X ia—, у. ,_1

q „ ■ S м P vI , p 2 v< h,_s       ■ ■. hs м     ^{1 [ H}l’

V' ^s м 2 p   S ^м

C 1 =        ,

ФУHSм где φ – коэффициент приемника воздушного давления; γ – объемный вес жидкости, залитой в микроманометр, H/м3; h – высота столба жидкости в микроманометре, м; Sм – площадь миде-левого сечения модели.

Аналогично для коэффициента подъемной силы

Cy = C 1 Y [ H ]-

Аэродинамические коэффициенты C x , C y даются в поточной системе координат, когда ось OX направлена по потоку, ось OY – перпендикулярно ей вверх.

Коэффициент момента тангажа относительно центра тяжести, расположенного на продольной оси модели можно определить по формуле mzt = Cy (xt - Cd ) , где Сd – коэффициент центра давления, определяемый по формуле mzt

C_d =    .

Cy

Здесь x _t – относительная координата положения центра тяжести модели, считая от носовой точки, в долях длины модели:

= xt xt b где b – хорда крыла или длина модели.

Заключение

Использование тензометрических весов позволяет значительно сократить время проведения эксперимента и повысить точность определения исследуемых величин. Отсутствие в тензометрических весах сложных поддерживающих устройств, характерных для весов механического типа, позволяет уменьшить влияние державок на обтекание исследуемой модели и тем самым повысить надежность результатов измерений.