Трехмерная интерполяция и подавление влияния приповерхностных неоднородностей при обработке гравиметрических данных

Гравиметрические данные являются источником ценной информации о глубинном строении крупных территорий и отдельных месторождений полезных ископаемых. Точность современной гравиметрической съемки увеличилась во много раз, в то же время методы обработки полевых данных остались прежними. Требуются пересмотр существующих стандартов редуцирования и разработка современных методов вычисления аномалий Буге, особенно в горных районах и районах со сложным рельефом местности.

Одним из важнейших этапов в обработке наблюденных измерений силы тяжести, после составления каталога исходных данных в редукции Буге, является создание цифровой модели гравитационного поля (матрицы). Определение значений аномального гравитационного поля ΔgБ в точках регулярной сети необходимо не только для визуализации полученной в ходе исследования информации в виде карты изоаномал, но и (что наиболее существенно) для формирования данных в целях дальнейшей интерпретации с использованием компьютерных технологий.

Подавляющее большинство методов восстановления гравитационного поля в узлах регулярной сети (интерполяция) подразумевает, что его значения заданы на горизонтальной поверхности: ΔgБ = ΔgБ(x,y) . Такая постановка задачи влечет за собой ряд ошибочных представлений. Во-первых, на практике в наблюденное поле вносит свою погрешность так называемый эффект разновысотности, обусловленный разной высотой пунктов наблюдений, который не учитывается при выполнении стандартных процедур редуцирования. Физическая суть данного эффекта заключается в возникновении специфических искажений гравитационного поля, обусловленных влиянием геометрического фактора – варьированием расстояний между возмущающими объектами и точками измерений за счет изменений высот        z t z(x, y)        поверхности наблюдений[6].

В горных районах или местности с резко расчлененным рельефом учет эф-

фекта разновысотности пунктов гравиметрических наблюдений продиктован очевидной практической потребностью. Современные гравиметрические съемки становятся более точными и детальными. В таких условиях рельеф дневной поверхности с перепадом высот даже в десятки метров будет вносить заметные искажения в результаты полевых наблюдений.

Аномальный эффект от горных пород верхней части разреза (ВЧР) вносит заметный вклад в данные гравиметрической съемки и является геологической помехой при изучении более глубинных объектов. Поэтому существует обязательный граф обработки данных полевых гравиметрических наблюдений, позволяющий уменьшить воздействие ВЧР – редукция Буге, включающая в себя поправки за промежуточный слой и влияние рельефа [7]. Традиционно плотность пород ВЧР принимают как некоторое постоянное значение = const для всей площади исследования [5], что во многих случаях не соответствует реальной геологической ситуации. Таким образом, наличие неучтенных петро-плотностных неоднородностей в промежуточном слое горных пород, использующемся при редуцировании гравитационного поля, может вызвать присутствие отдельных ложных аномалий Δg Б либо «зашумление» общей картины распределения аномалий силы тяжести.

Как правило, для интерполяции данных гравиметрической съемки в точки регулярной сети используются различные двухмерные методы, учитывающие лишь различия в плановом местоположении исходных и результативных точек f = f(x,y) (метод взвешенных расстояний, крайгинг, метод минимальной кривизны и т.п.). Каждый из этих алгоритмов достаточно эффективно используется для определенного типа данных, но ни один из них не учитывает физические особенности потенциального поля, что может повлечь за собой появление специфических помех негеологической природы в пространственном распределении аномалий силы тяжести ΔgБ. Для изучения неодно- родной по плотности толщи горных пород промежуточного слоя успешно применяется комплексирование с другими геолого-геофизическими методами (в частности – с сейсморазведкой), позволяющими получить более целостное представление о свойствах пород ВЧР [3,4]. Однако такой подход не всегда возможен из-за высокой стоимости исследований или геоморфологических условий изучаемой территории.

Аналитические истокообразные аппроксимации широко используются для различных целей, таких как пересчет полей в верхнее полупространство, вычисление производных (первообразных), фильтрация случайных компонент поля, сжатие информации о поле (метод квадродерева). Авторами предлагаются методы построения цифровых моделей гравиметрических данных, основанные на применении аналитических аппроксимаций, позволяющие уменьшить вклад «эффекта разновысотности» и геоплотностных неоднородностей ВЧР в суммарный аномальный эффект Δg н .

Несмотря на то, что гравитационные наблюдения проводятся преимущественно по предварительно разбитой сети прямолинейных профилей, при построении гравиметрической карты значения в исходных точках будут пересчитываться в новую регулярную квадратную сеть с заданным шагом между точками ∆x . Это связано с особенностями компьютерной обработки данных – для визуализации изображения, как правило, требуются цифровые модели поля в виде матриц Δg(x,y) . Предлагаемый алгоритм 3D-интерполя-ции позволяет уменьшать ошибки, связанные с влиянием криволинейности поверхности наблюдений и повышать точность построения карт Δg(x,y,z) .

Для решения задач интерполяции под каждую точку наблюдения помещают сингулярный источник поля (например шар) на глубину z1 от поверхности рельефа в данной точке [1], т.е. расположение точечных масс повторяет конфигурацию рельефа. Массы источников а определяются путем решения системы линейных алгебраических уравнений (СЛАУ) aG=d g, где G - матрица, элементы которой представляют собой истокообразные функции (поля элементарных источников при а = 1 г/см3), a g - вектор исходных значений поля Δgн(xi,yi,zi), заданных на земной поверхности S = S(xi,yi,zi). На практике такие системы решают итерационными методами (метод Зейделя, методы градиентного спуска и др.), позволяющими наиболее корректно восстановить приближенное равенство правой и левой частей СЛАУ.

Система линейных уравнений для алгоритма 3D-интерполяции будет выглядеть следующим образом:

о g * 5 х , y , z ( x , y ) ! t A 1 ~ ri G)x H x„y H y i , z_y ( x , y ) 8 _; (1)

G | ±,______________Z1z (x, y)           , ri 2/ 3(x H xi) G (y H y) G (z,,r(x,y))2Г, (2)

где z1,r(x, y) T z(x, y)H zr(xi, yi);(xi, yl) x pr; z(x,y) – вертикальные координаты поверхности S, на которой заданы значения U*; zr(xi,yi)>0 – вертикальная координата значений αri, параметр вычислительной схемы; ~ri T ~r5xi,yi,zr(xi-,yi)8 - некоторые коэффициенты, удовлетворяющие условию минимального расхождения исходной Δgн(xi,yi,zi) и восстанавливающей Δg* (xi,yi,zi) функций в евклидовой метрике.

Оптимальной, по В.И. Аронову, считается глубина расположения источников, находящаяся в пределах одного-двух шагов сети наблюдения ∆x≤z1≤2∆x [1]. Такой критерий выбора z1 можно объяснить тем, что поле элементарных источников, расположенных ниже обозначенного предела 2∆x, не сможет полностью «выбрать» высокочастотную составляющую наблюденного гравитационного поля, а в противном случае возможно появление неконтролируемых искажений в восстановленном поле (здесь и в дальнейшем рассматривается 3D-вариант использования аналитических аппроксимаций). Таким образом, варьируя глубинами распо- ложения эквивалентных источников – параметром z1, удается построить некоторый фильтр, позволяющий приближенно выделять эффект от интересующей толщи горных пород. При этом будет автоматически производиться подавление помех, нарушающих гармонический характер поля [2].

При конкордантном земной поверхности расположении эквивалентных источников задача 3D-интерполяции поля будет решаться наилучшим образом. Для обеспечения большей точности построений достаточно применять двухуровневую конструкцию с глубинами [z1] 1 =(3-4)∆x и [z1] 2 ≈∆x , отвечающими за низкочастотную компоненту наблюденного поля и его высокочастотную составляющую соответственно.

Применительно к исследованию неоднородной плотности ВЧР целесообразно было построить аппроксимирующую конструкцию, в которой эквивалентные источники располагаются на горизонтальной плоскости z = const , отвечающей подошве промежуточного слоя, использующегося при проведении редукции Буге. Таким образом, разность восстановленного по такой конструкции гравитационного поля Δg* и наблюденного поля Δg н должна в какой-то мере отобразить распределение геоплотностных неоднородностей в промежуточном слое.

Основные возможности предлагаемых методов можно охарактеризовать на следующих примерах.

Модельный пример 1. Построена модель возмущающих объектов – совокупности шарообразных тел с различными физическими (массы) и геометрическими (глубина залегания центра и радиус тела) характеристиками. Гравитационное поле ag(xi,yi,zi) этой модели (рис. 1, А) рассчитывалось в узлах нерегулярных сетей, горизонтальные координаты которых xi, yi определялись путем генерации случайных чисел, равномерно распределенных в заданной области. В качестве поверхности поля использовалась реальная цифровая модель рельефа земной поверхности гор- ного района, обладающая перепадом высот порядка 1600 м (рис. 1, Б). Размер площади составлял 22 215 км, плотность сети

– приблизительно 30 точек на 1 км2 (что отвечает гравиметрической съемке масштаба 1:50 000).

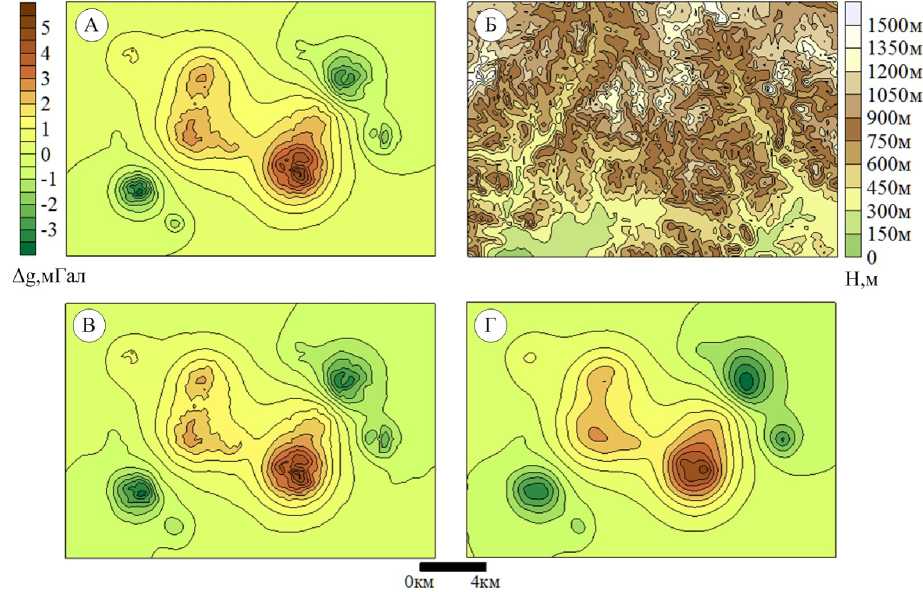
Рис. 1 . Сопоставление различных методов восстановления гравитационного поля: А – исходное поле; Б – рельеф поверхности задания поля; В – поле, восстановленное 3D-интерполяцией; Г – поле, восстановленное 2D-интерполяцией (крайгинг)

Результат 3D-восстановления гравитационного поля гармоническими функциями представлен на рис. 1, В. Для сравнения показано восстановление поля методом крайгинга с автоматическим построением вариограммы в узлы той регулярной сети.

Построение изоаномал гравитационного поля методом крайгинга дает существенный сглаживающий эффект даже на простых моделях, несмотря на соблюдение заданной точности восстановления [2]. Как очевидно, точность трехмерного метода выше точности двухмерных примерно в 2-3 раза, в последнем случае отмечается заметное сглаживание локальных особенностей поля (рис. 1, Г). Результаты 3D-восстановления при различных сетях задания исходного поля характеризуются невязкой, не превышающей 2э^0.03-0.05) мГал в подавляющем большинстве точек, что свидетельствует о достаточной устойчивости алгоритма к изменению структуры исходных данных.

Модельный пример 2. Представлены модельные гравитационные поля ΔgБ, рассчитанные от разноглубинных источников поля в точках регулярной сети на реально существующем рельефе с перепадом высот порядка 600 м (рис. 2). В первую модель были добавлены локализованные в ВЧР источники поля в интервале глубин промежуточного слоя, ассоциируемые с неоднородностями ВЧР (рис. 2, I, А). Во второй модели предполагалась латеральная изменчивость плотности горных пород промежуточного слоя δ = δ(x, y), что в вычислительном плане отвечало кусочно-призматической аппроксимации промежуточного слоя на всем его протяжении. Эквивалентные источники размещались на плоскости, отвечающей нулевой отметке высот z = 0, точность аппроксимации полей в обоих случаях составляла менее 29.15 мГал. Фильтрационные возможности метода характеризуют карты разности исходных и восстановленных по апппроксимационным конструкциям полей.

В первом случае в «разностном» поле четко пространственно локализуются источники поля, находящиеся выше используемых точечных масс. Однако выделенная нами компонента поля обусловлена не только объектами, расположенными в слое ВЧР, но и высокочастотной

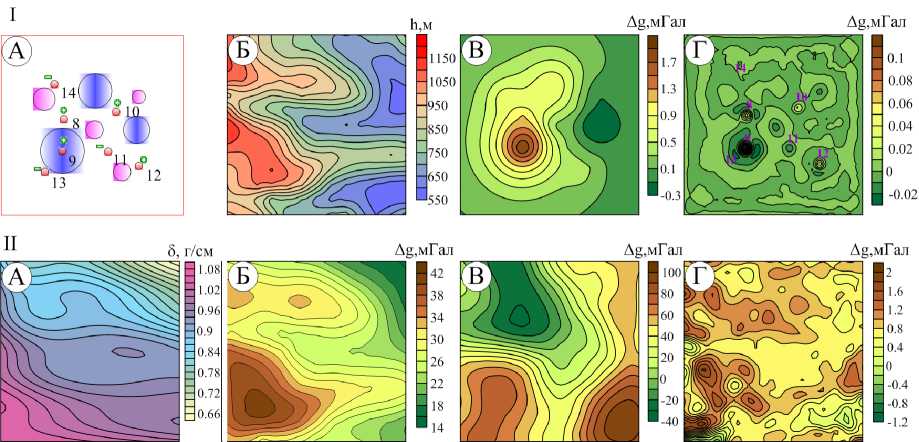
Рис. 2 . Модельные примеры определения плотностной неоднородности ВЧР при помощи аналитических аппроксимаций: I – модель разноглубинных шарообразных источников гравитационного поля: А – расположение источников поля (черными сферами обозначены источники, расположенные в промежуточном слое); Б – рельеф земной поверхности; В – модельное гравитационное поле; В – разность модельного и восстановленного полей; II – модель промежуточного слоя с латеральной изменчивостью плотности: А – плотность промежуточного слоя δ = δ (x,y); Б – гравитационное поле модели промежуточного слоя; В – модельное гравитационное поле, включающее в себя влияние промежуточного слоя и глубинных источников; В – разность модельного и восстановленного полей

составляющей от более глубинных гравитирующих объектов. Как очевидно, влияние этих объектов является сравнительно слабым по сравнению с геоплотностными неоднородностями ВЧР.

Во втором случае можно проследить общий характер пространственного распределения модельной плотности ВЧР δ = δ (x,y) . Алгоритм 3D-интерполяции позволил локализовать две высокоамплитудные аномалии (рис. 2, II Г). Следует отметить, что большая часть высокочастотной компоненты от глубинных источников редуцирована.

Таким образом, оба примера показывают, что возможности данного метода позволяют провести локализацию геоплот- ностных неоднородностей промежуточного слоя и существенно ослабить создаваемые ими аномальные эффекты.

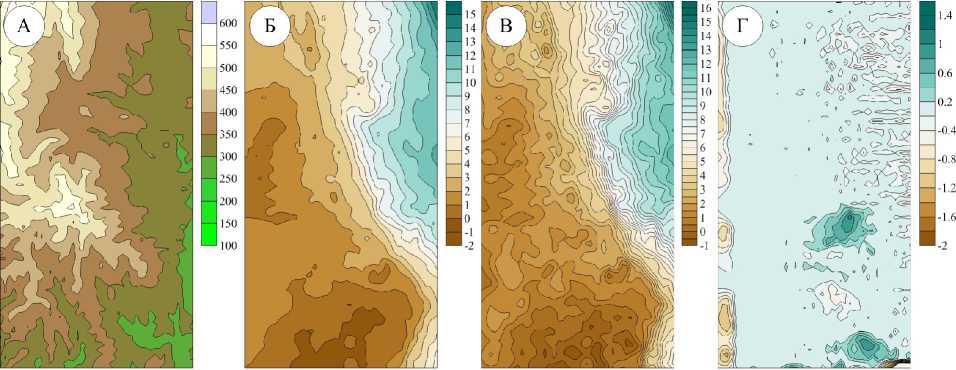
Рассмотрим практический пример построения цифровой модели (матрицы) гравитационного поля ΔgБ одного из нефтеперспективных участков Среднего Урала по гравиметрической съемке масштаба 1:50 000. Максимальный перепад высот рельефа местности составляет 427 м (рис. 3, А). Для построения матрицы были использованы значения аномального гравитационного поля в редукции Буге с плотностью промежуточного слоя 2.67 г/см3, высоты гравиметрических пунктов и массив высотных отметок участка выполненной съемки. Для 3D-интерполяции была использована двухуровневая аппроксимационная конструкция с согласным земной поверхности расположением точечных источников. Карта изоаномал гравитационного поля в редукции Буге с плотностью промежуточного слоя 2.67 г/см3 приведена на рис. 3, В. Среднеквадратическая погрешность в узлах нерегулярной сети составила ε = ±0.07 мГал. Аналогичная задача решалась с помощью стандартного алгоритма крайгинга, однако погрешность получилась более чем в 2 раза выше: ε = ±0.16 мГал (рис. 2, Б). Гравиметрическая карта, построенная при помощи крайгин-

Для выявления локальных плотностных неоднородностей в промежуточном слое была построена карта разности цифровой модели гравитационного поля Δg Б и результата ее аппроксимации эквивалентными источниками, находящимися на уровне z1=100 м . В результате выделены ряд крупных аномалий от приповерхностных источников с амплитудой около 1 мГал и ряд слабоинтенсивных аномалий, также предположительно связанных с влиянием промежуточного слоя.

га, является более сглаженной.

Н,м                        Ag,MFaa                     Ag,MT^                     Ag,Mfo

1 KM

Рис. 3. Результаты 3D-интерполяции гравиметрических данных (Средний Урал): 1 – карта изогипс рельефа местности, м; карты изоаномал гравитационного поля, построенные: 2 – методом крайгинга, 3 – методом 3D-интерполяции; 4 – карта разности, отражающая влияние приповерхностных неоднородностей

Вывод

Рассматриваемые методы обработки гравиметрических данных, базирующиеся на аналитических аппроксимациях, адекватны физико-геологическим особенностям проведения исследований. Применение этих методов позволяет повысить точность построения цифровых моделей аномального гравитационного поля и подавить влияние геоплотностных неоднородностей ВЧР, используя минимум априорной информации. Представленные алгоритмы просты в математическом исполне- нии, обладают высоким быстродействием и достаточно эффективны при решении практических задач. Включение их в граф обработки данных полевых гравиметрических наблюдений способно повысить точность построения гравиметрических карт и достоверность последующих интерпретационных построений.

Работа выполнена при поддержке РФФИ (грант № 11-05-96013) и программы исследований ОНЗ РАН (проект 12-Т-5-2012).