Трехмерное моделирование акустического поля в скважине, возбуждаемого источником в пласте

Измерение интенсивности акустического шума, в скважине является одним из действенных методов анализа, технического состояния скважины и определения гидродинамических свойств коллекторов. Анализ спектральных характеристик акустических шумов, вызванных фильтрацией флюида, в породе пласта, (фильтрационные шумы) [1], применяется для обнаружения отдающих и принимающих интервалов пласта и определения типа поступающего в ствол скважины флюида. Спектр фильтрационного шума, лежит в полосе 2-20 кГц, что соответствует экспериментальным данным [2]. Развитие математических методов для

повышения качества и надежности интерпретации данных шумометрии является актуальной задачей.

В [3] описана численная модель, позволяющая рассчитывать акустические поля, генерируемые фильтрационным потоком в пласте, в предположении наличия вращательной симметрии. По результатам моделирования в спектрах были обнаружены достаточно широкие интервалы резонансных частот, где амплитуда акустического поля существенно возрастает. Был проведен анализ чувствительности этих резонансных мод к геометрии скважины, свойствам пород-коллекторов и фазовому составу флюида, что позволило начать разработку новых подходов интерпретации [4,5].

В данной работе рассматривается трехмерная задача моделирования акустического поля в скважине с целью учета влияния на спектр, в том числе на возбуждение резонансных мод, таких эффектов, как наличие перфорационных отверстий и локализованных по азимуту трещин.

2.    Постановка задачи

Рассматривается трехмерная постановка задачи в декартовой системе координат (ж, у, г). Область моделирования П представляет собой прямоугольный параллелепипед {|ж| 6 L_x/2, |у| 6 Ly /2, |г| 6 L_z /2}, г де L_x, L_y, L_z — длины сторон по осям ж, у и г соответственно. Модель включает в себя цилиндрическую скважину радиуса rwen, заполненную флюидом. Ее ось параллельна оси г и проходит через центр параллелепипеда. Скважину окружает пласт, состоящий в общем случае из нескольких поперечных слоев толщиной Ні, г = 1,..., N, где N — количество слоев, ^і=і Щ = L_z. В некоторых из слоев пласта располагаются источники акустического шума. На данном этапе разработки модели каждый слой считается сплошным, изотропным и изотермическим.

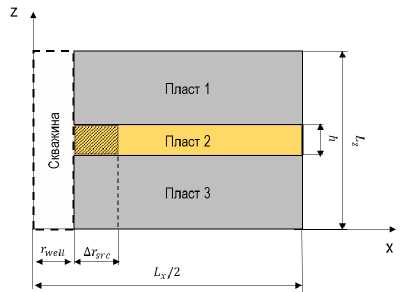
Конфигурация источника рассматривается в двух вариантах: кольцевой и векториальный. Кольцевой источник предполагается осесимметричным и занимает область по радиусу в околоскважинной зоне пласта, соответствующую кольцу rwen 6 г 6 rwen + Arsrc (рис. 1), где г = ^ж² + у² — радиальная координата, Arsrc — радиус зоны источника. Секториальный источник локализован в секторе кольца того же радиуса и занимает область Ө1 6 Ө 6 Ө2 (рис. 2), где Ө — азимутальная координата, Ө1, Ө2 — границы углового сектора.

а)

Рис. 1. Типичная геометрия модели с кольцевым источником и тремя слоями в пласте: а) продольный разрез модели, б) поперечный разрез слоя

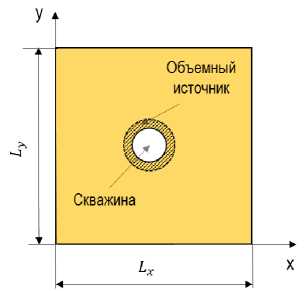
б)

Распространение волн в пласте моделируется при помощи линейной системы уравнений упругости, записанной в форме волнового уравнения Навье:

p_sd 2 u ^{( s )} - V • T = F src (ж,у,г,t),

где t — время; u^(s) — вектор смещений частиц упругой среды; p ₈ — плотность упругой среды; F_src — объемный источник, отвечающий за генерацию акустического шума. Тензор T — отклонение от стационарного значения тензора напряжений упругой среды, определяющееся по закону Гука:

T = А ( v • u^(s)) I + 2G • 1/2 ( (Vu * ⁸ ) )⁷

+ Vu(s)) ,

где А, G — параметры Ламе для упругой среды, I — единичный тензор второго ранга.

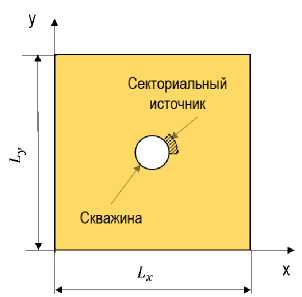
Рис. 2. Геометрия модели с секториальпым источником: поперечный разрез слоя

Распространение волн в скважине описывается уравнением акустики:

Pf ^d?y ^— k_f ^Ay = О,

где у — скалярный потенциал, определяющий вектор смещения частиц флюида u^(f) = Vy/pf; kf — модуль всестороннего сжатия флюида; pf — плотность флюида. В условиях на интерфейсе скважина-порода используется выражение р — —Э^у для отклонения от стационарного значения давления флюида.

Источник звуковых колебаний Fsrc занимает область в пласте, где происходит приток флюида в скважину. Его интенсивность предполагается неизменной по вертикали и азимуту и обратно пропорциональной кубу радиальной координаты в силу снижения скорости фильтрации по мере удаления от скважины. На достаточном расстоянии от скважины, а также в слоях с низким притоком флюида интенсивность источника задается равной нулю. Таким образом, выражение для источника записывается в виде

F src (ж, У, ^Z, ^t) — er

{

A^ well /^)³^ (t),

О, else,

^ well 6 Г 6 ^ well + AT src , Zi < Z < Zi + Hi,

где e_r — единичный радиальный вектор цилиндрической системы координат, задающий направление действия источника; А — амплитуда источника; S/t) — сигнал, генерируемый источником; Zi — нижняя граница слоя пласта.

На внешних границах расчетной области при ж — ±Т_ж/2, и ли у — ±L_y /2, и ли z — ±L_Z /2 используются простейшие неотражающие граничные условия [6]. На интерфейсе между скважиной и пластом заданы следующие условия:

^Trr = —^р;

T._z — 0; u.⁸ ) — u^ ) .

Здесь T_rr. T_rz. u.⁸. и. )

— компоненты соответствующих величин в цилиндрической системе координат.

3.    Метод спектральных элементов

Для численного решения рассматриваемой гиперболической системы (1) - (2) с заданными условиями на интерфейсе (3), однородными начальными условиями и неотражающими граничными условиями применяется метод спектральных элементов [7], реализованный в открытом коде SPECFEM3D Cartesian [8].

Дадим вариационную формулировку задачи (1) - (3), умножив скалярно (1) на произвольную вектор-функцию w(x,y,z)₁ а (2) — на произвольную скалярную функцию ш(ж,^,г) и проинтегрировав оба уравнения по областям w_s (упругая среда) и wj (жидкая среда) по частям:

j p_sw • d2 u ^(s

Ш8

¹) dw — j w • ( T • n ) ds + j V w : T dw = j F src • w dw;

Эш8

ш8                 ш8

j pjwd^dw — I kjw n •Vpds + ^^7 Vw -V^dw = 0. шу                 Эшу                   шу

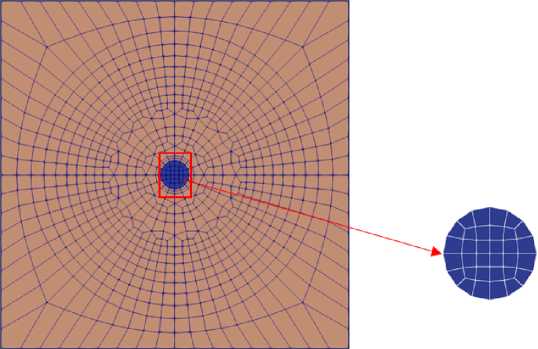
Расчетная область Q = w_sUwj разбивается на некоторое количество п_е объемных конечных элементов Q_e, е = 1,..., п_е, Q = U^E 1 Q_e, имеющих форму шестигранников в качестве объемных элементов (рис. 3). Граница расчетной области разбивается на пь поверхностных конечных элементов, которые представляют собой четырехугольники dПь_; b = 1,...,пь, d Q = Ц= 1д Qb-

а)

Рис. 3. Разбиение расчетной области на элементы: а) вид сверху, б) вид сбоку

б)

Описание процедуры интегрирования слагаемых в системе (4) по элементам приведено в приложении. В результате система (4) сводится к системе обыкновенных дифференциальных уравнений относительно значений искомых полей в узлах GLL-сетки в каждом элементе, см. приложение. Полученная система уравнений может быть записана следую щим образом:

М (^U + С ^(s^U + К ^(s^U = F ; М^(j ) Ф + С (⁷ ) Ф + К (⁷ ) Ф = 0,

где U — вектор, сод сржащий значения u^(s) во всех уз л ах сетки, Ф — вектор значений ^ в узлах сетки. Матрицы М^(s\ С^(s\ К ^(s) возникают при интегрировании первого, второго и третьего слагаемого соответственно в первом уравнении системы (4), F — вектор, полученный при интегрировании правой части в (4). Матрицы М(⁷ ), С(⁷ ), К(⁷ ) выводятся аналогично из второго уравнения в (4).

Благодаря использованию сетки GLL матрицы М оказываются диагональными, что упрощает явную разностную схему для интегрирования по времени. Мы применяем схему Ньюмарка типа предиктор-корректор второго порядка аппроксимации по времени.

Аппроксимация решения задачи по пространству в методе спектральных элементов определяется двумя параметрами: А А — характерный размер элемента и тц — максимальная степень интерполяционных многочленов Лагранжа, используемых для представления функции на элементе.

В данной работе при моделировании применялся базис из многочленов Лагранжа с Т = 4. Соответственно на каждый объемный элемент приходится по 125 узлов сетки GLL, а на каждый поверхностный — 25 узлов сетки GLL (5 по каждому из направлений).

4.    Результаты моделирования для случая кольцевого источника4.1.    Параметры моделирования

Рассматривается постановка задачи, представленная на рис. 1, с тремя слоями в пласте (N = 3). Геометрические параметры модели следующие: Н2 = Һ = 0.24 м, rwen = 0.12 м, Arsrc = 0.24 м, L_x = L_y = L = 2.88 м, L_z = 6.24 м, Н1 = Н3 = Н = 3 м.

Скважина заполнена газом с параметрами, соответствующими метану при давлении 2 • 107 Па и температуре 343 К. Порода представляет собой известняк и моделируется линейной упругой средой. Упругие свойства газа и породы представлены в табл. 1.

Таблица!

Свойства газа и породы

	Газ (метан)	Порода
Плотность ( р), к г/м3	123	2125
Скорость продольной ВОЛНЫ (Гр), м/с	535	3953
Скорость поперечной волны (щ), м/с	0	2603

Спектр сигнала S (t), генерируемого источником, является равномерным в диапазоне от 2 до 6 кГц с шагом дискретизации в 50 Гц. Амплитуда источника А равна 5 • 10-4 Па/м.

Построенная конечно-элементная сетка содержит порядка 48 тысяч элементов. «Минимальный» и «максимальный» линейный размер элемента, оцениваемый через кубический корень из объема элемента в скважине, составляют 0.04 м и 0.05 м соответственно. В пласте линейный размер элемента варьируется от 0.04 м вблизи скважины до 0.19 м на внешней границе расчетной области.

Минимальная длина волны Amin гармонического по времени акустического поля в скважине, соответствующая максимальной частоте источника, равна 0.09 м. Таким образом, в скважине на длину волны в среднем приходится около двух конечных элементов. Относительная погрешность решения на данной сетке в Г2-норме составляет 2% в скважине, что было оценено по дополнительным расчетам при проверке сеточной сходимости.

Время моделирования 100 мс было выбрано из условия выхода на периодический режим колебаний в скважине. Количество шагов по времени составляет примерно 250 000.

4.2.    Анализ акустического поля в скважине

В [3,4] представлены результаты исследований спектров акустического давления в скважине в осесимметричной постановке задачи, полученные посредством моделирования двумерным кодом на основе конечно-разностной схемы [9]. В спектрах были обнаружены интервалы резонансных частот, на которых происходит существенное усиление сигнала.

Положение резонансных частот J_xes приближенно оценивается на основе решения уравнения Гельмгольца в цилиндрической скважине с абсолютно жесткой стенкой:

fU = ^ \( £ ^ + ( X ) •' = 1'2""'               ⁽⁶>

2"   у Г well у     у Az У где с — скорость звуковой волны в газе, /(0) — корни производной функции Бесселя J0(ж), Xz — длина волн, распространяющихся вдоль оси г.

Для случая трехмерного моделирования распределение спектра акустического давления вдоль ствола скважины (называемого далее спектрограммой) представлено на рис. 4. Распределение взято для координаты r = 0.01 м.

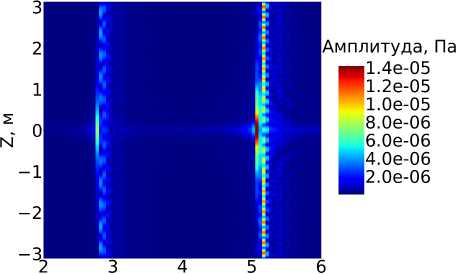
Частота, кГц

Рис. 4. Спектрограмма акустического давления для случая кольцевого источника

Для анализа осесимметричных решений, полученных 2D- и ЗВ-кодами, рассмотрим спектры в точке г = 0, представленные на рис. 5а. Видно, что резонансы, соответствующие ЗВ-моделированию, смещены вправо.

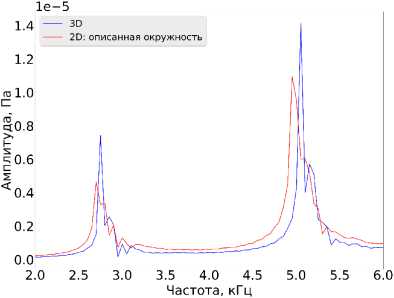
а)

Рис. 5. Спектры акустического поля в точке г = 0, г = 0.01 м, полученные двумерным и трехмерным моделированием: а) случай описанной окружности, б) случай вписанной окружности в многоугольник, имитирующий скважину на ЗВ-сетке

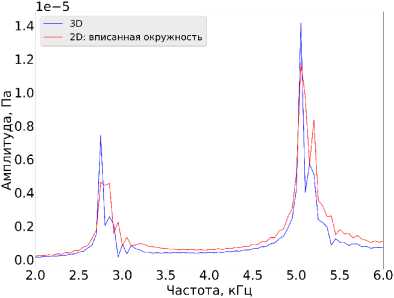
б)

Данный сдвиг вызван тем, что для построения сетки используются элементы первого порядка, в результате чего скважина в поперечном сечении представляет собой правильный многоугольник (при текущих параметрах сетки — 16-угольник), радиус описанной окружности для которого равен rweii.

Для оценки эффективного радиуса скважины reff, при котором резонансы совпадают, был проведен расчет с помощью двумерного кода, в котором радиус скважины был задан равным радиусу, вписанной в многоугольник окружности rin = rweii cos (^/16) = 0.118 м. Сравнение спектров показано на рис. 56. Из него видно, что сдвиг резонансов практически незаметен и форма спектров схожа между собой за некоторым отличием вблизи резонансов. Таким образом, reff для трехмерного случая можно приближенно оценить значением rweii cos (^/п), где п — число сторон многоугольника, имитирующего скважину в ЗВ-сетке, и использовать его для построения сетки в скважине.

5.    Результаты моделирования для случая секториального источника

Рассмотрим конфигурацию с секториальным источником, представленную на рис. 2. Геометрические параметры модели, физические свойства среды, а также параметры моделирования описаны в разделе 4.1 (при этом reff = 0.118 м). Угловой размер источника составляет 0 6 Ө 6 л/8, что соответствует сектору 16-угольника.

Проанализируем спектрограммы акустического давления на оси скважины (рис. 6).

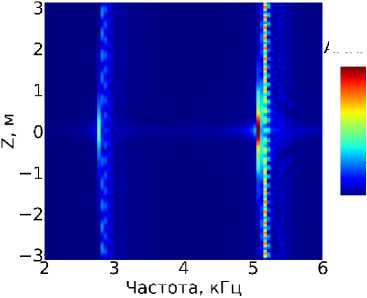
1.4е-05

1.2е-О5

1.0е-05

8.06-06

6.0е-06

4.0е-06

2.06-06

а)

Амплитуда, Па

б)

Амплитуда, Па 8.06-07 7.06-07

б.Ое-07

5.06-07

4.06-07

З.Ое-07

2.06-07

1.06-07

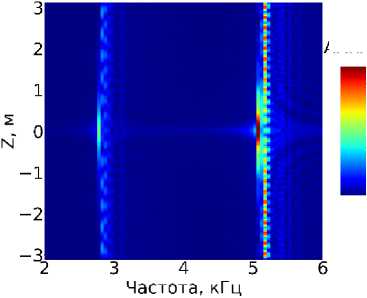
Рис. 6. Спектрограмма, акустического давления на оси скважины: а) кольцевой источник, б) секториальный источник

Видно, что для секториального источника, возбуждаются те же резонансные моды, что и для кольцевого источника. Изображения для данных случаев очень схожи, а. амплитуды резонансных мод отличаются приблизительно в 16 раз, что соответствует отношению размеров излучающих областей по азимуту, т.е. силы сигнала.

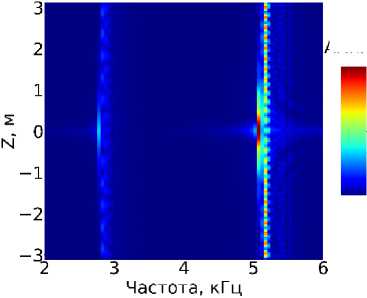
Ниже приведены спектрограммы на. удалении от оси скважины, для координаты r = 0.06 м, для случая кольцевого (рис. 7) и секториального (рис. 8) источников. Из них видно, что в случае секториального источника, появляется большое количество дополнительных резонансов, вызванных возбуждением азимутальных мод, амплитуда, которых зависит от угла. Ө.

Амплитуда, Па

6.0е-06

5.06-06

4.06-06

3.0е-0б

2.06-06

1.0е-06

Рис. 7. Спектрограмма акустического давления для координаты r = 0.06 м для случая кольцевого источника.

Формула (6) для оценки резонансных частот f^ легко обобщается для этого случая:

с

рl,m _ ___

^Jres “ 2Ц

( Д у + ( 2Т ) ².,,„ = 1,2,...,

У rwell у    V^y

где ц^(т) — корни производной функции Бесселя J'_m (ж).

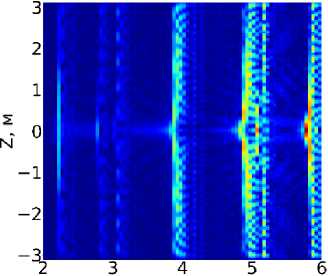
Частота, кГц

а)

Рис. 8. Спектрограммы акустического давления для координаты т = 0.06 м для случая сектори-ального источника: а) при азимуте Ө = 0, б) при азимуте Ө = тт/2

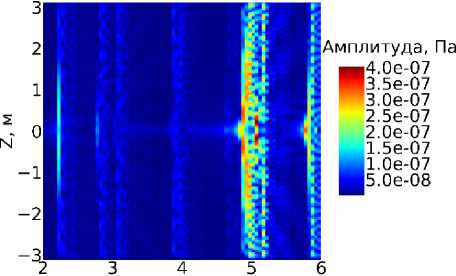
Частота, кГц

б)

В табл. 2 приведены значения резонансов (7) для данной конфигурации модели. Из нее видно, что некоторые резонансные моды (например, при m = 0 и m = 2) расположены оченв близко друг от друга.

Т а б л и ц а 2 Значения резонансов для рассматриваемой скважины

Порядок функции Бесселя	Номер корня производной функции Бесселя
	1 = 1	1 = 2	1 = 3	1 = 4	1 = 5	1 = 6	1 = 7
m = 0	2722 Гц	4985 Гц	7228 Гц	9466 Гц	11 702 Гц	13 937 Гц	16171 Гц
m = 1	1308 Гц	3788 Гц	6065 Гц	8317 Гц	10 560 Гц	12 800 Гц	15 037 Гц
m = 2	2170 Гц	4765 Гц	7083 Гц	9357 Гц	11615 Гц	13 864 Гц	16108 Гц
m = 3	2985 Гц	5695 Гц	8061 Гц	10 363 Гц	12 639 Гц	14 901 Гц	17155 Гц
m = 4	3778 Гц	6595 Гц	9010 Гц	11342 Гц	13 639 Гц	15 916 Гц	18181 Гц

Уширение интервалов резонансов, обычно наблюдаемое в системе скважина-порода, ведет к тому, что близко расположенные резонансы накладываются друг на друга в спектре, что видно на рис. 8 в районе 5 кГц.

6.    Заключение

Для исследования акустических шумов, порождаемых фильтрационным потоком из пласта в скважину, построена трехмерная численная модель. В ней используется метод спектральных элементов, реализованный в открытом коде SPECFEM3D Cartesian.

Проведено сравнение результатов моделирования осесимметричного случая с расчетами по конечно-разностному двумерному коду. Показано, что для хорошего совпадения спектров необходимо вводить предложенную коррекцию радиуса скважины, которая учитывает неточность представления круговой скважины многоугольником в сеточной области метода спектральных элементов.

Для имитации шума флюида, вытекающего из перфорационного отверстия, были рассчитаны трехмерные поля, возбуждаемые секториальным источником. По результатам моделирования выявлено, что осевая спектрограмма, т.е. рассматриваемая для точек на оси скважины, полностью сохраняется при переходе от кольцевого к секториальному источнику. Это позволит на данном этапе ограничиться быстрыми двумерными расчетами при разработке алгоритмов интерпретации зон притока (в таких задачах требуется выяснить местоположение, фазовый состав и величину притока). На следующем этапе понадобится оценка влияния на осевую спектрограмму трехмерных эффектов, связанных с изменением свойств пласта по азимуту (в частности, от перфорационных отверстий), интерференцией соседних притоков и т.п., что потребует дальнейших исследований с помощью построенной модели.

Авторы благодарны Шлюмберже за разрешение опубликовать представленные результаты.

Приложение. Дискретизация модели методом спектральных элементов

Здесь представлен переход от системы (4) к (5).

Для каждого объемного элемента П_е задается отображение (ж, у, z) ^ (ОйХ ) в параметрический элемент в форме куба (поверхностные элементы отображаются в квадрат), — 1 6 £ 6 1, — 1 6 у 6 1, — 1 6 С 6 1. Предполагается, что отображение является линейным по каждому из направлений, т.е. рассматриваются элементы первого порядка. Для задания отображения используются 8 угловых точек x_a, a = 1,..., 8, шестигранника (для поверхностных элементов - 4 угловые точки). Соотношение, связывающее произвольную точку x в П_е с произвольной точкой (^,т),С ) ^в параметрической ячейке, может быть записано в виде

8 ^{x (}£, У, <) = ^ N_a Д, у, () xa, a=1

где Т^ДОрД ) = іДОір (у)^7(С); a,/3,7 = 0,1 — произведения линейных интерполяционных многочленов Лагранжа.

Для решения задачи (4) все интегралы по расчетной области П и по границе расчетной области dП разбиваются на подынтегралы по объемным и поверхностным элементам соответственно. Функции на элементах представляются интерполяционными многочленами Лагранжа L_a(O высокого порядка п/, определенными на узлах Гаусса-Лобатто-Лежандра (далее GLL) £_а, a = 0,... ,п/, которые являются корнями уравнения вида

(1 — 02) P« t (Д = 0, где Р«г — многочлен Лежандра порядка п/. Произвольная скалярная функция f, а также компоненты векторной функции, представляются на элементе Пе в виде

«г f (x (е,уд))= 52 l. (ol9 (p)l. (с), «.3.7=0

где f“^7 — значение функции f в узлах GLL.

Интегрирование внутри элемента производится при помощи квадратуры Гаусса-Лобатто-Лежандра:

/

Q e

«г f (x)dn « 52 ^.^ ^ - .!.■,

«,£,7 =0

где ш_а, a = 0, ...,п/ — веса интегрирования, ассоциированные с узлами GLL, J^ — якобиан отображения элемента И_е в соответствующую параметрическую ячейку, вычисленный в узлах GLL. Посколвку частв узлов может принадлежать нескольким элементам, которые соприкасаются друг с другом по граням, ребрам или вершинам, вклады таких узлов в систему уравнений суммируются с весами по всем элементам, которым этот узел принадлежит, при этом на границе упругой среды с жидкостью учитываются условия (3), см. [8].

Таким образом, после применения вышеописанной процедуры интегрирования ко всем слагаемым в системе (4), в том числе к слагаемым, содержащим взятие градиента, см. [7], задача сводится к решению системы обыкновенных дифференциальных уравнений относительно значений искомых полей во всех точках GLL по всем элементам (объемным и поверхностным).