Трехмерное моделирование изменений температуры, ветра и химического состава атмосферы земли, обусловленных активностью солнца

Как известно, физическими агентами, осуществляющими переменное по времени внешнее воздействие на атмосферу Земли, являются электромагнитная и корпускулярная радиация. При этом изменения электромагнитной радиации в цикле активности Солнца в существенной мере зависят от длины волны, убывая с ее ростом. Корпускулярная радиация, обусловленная протонными вспышками на Солнце и высыпаниями релятивистских электронов из радиационных поясов Земли в периоды геомагнитных возмущений, приводит к дополнительному образованию окислов азота и водорода [Porter et al., 1986], разрушающих озон в химических каталитических циклах (более подробно см. [Криволуцкий, Репнев, 2009; Криволуцкий и др., 2011]).

Спутниковые наблюдения вариаций солнечного спектра в ходе 11-летнего цикла солнечной активности (по данным за три солнечных цикла – 20-, 21- и 22-й) позволили оценить их изменчивость: примерно 100 % в области 140–155 нм, 70 % для длины волны 160 нм, 50 % для 170 нм и 20 % для 180 нм. Из приведенных данных видно, что эти изменения затухают с увеличением длины волны. В области длин волн более 100 нм важным источником ионизации и диссоциации в атмосфере является эмиссионная линия водорода Lα, которая в спокойных условиях несет бóльшую энергию, чем весь остальной спектр в области коротких волн. Общий поток излучения в этой линии, а также ее форма изменяются в течение солнечного цикла от (2.5…3.0)·1011 фотон см–2 с–1 в минимуме солнечной активности до (4.0…6.0)·1011 фотон см–2 с–1 в максимуме [Brasseur, Solomon, 2005]. Измерения со спутников, проведенные в период 23-го солнечного цикла, показали, что затянувшийся минимум активности сопровождался беспрецедентным понижением потока УФ-радиации.

Следует отметить, что вариации УФ-радиации Солнца используются при фотохимическом моделировании и исследовании различных механизмов солнечно-атмосферных связей. В то же время область видимого спектра, в которой находится основная энергия (порядка 1367 Вт м–2), поступающая на Землю от Солнца (солнечная постоянная), меняется очень слабо (~0.1 %). Такие слабые колебания на фоне ошибок измерений стало возможно зафиксировать лишь в результате долговременного мониторинга со спутников на протяжении нескольких циклов солнечной активности.

В настоящей работе представлены результаты трехмерного моделирования, иллюстрирующие атмосферные эффекты сильного понижения УФ-радиации в годы минимума 23-го цикла, а также пример долговременных последствий воздействия частиц.

• 1.    Моделирование воздействия факторов сол нечной активности на атмосферу Земли

  Трехмерные модели являются мощным инструментом современных исследований и используются при решении различных задач. Ниже приводятся краткое описание численных моделей, которыми располагает Лаборатория химии и динамики атмосферы Центральной аэрологической обсерватории (ЦАО): трехмерной фотохимической модели средней атмосферы и тропосферы и модели глобальной циркуляции тропосферы, средней атмосферы и нижней термосферы [Krivolut-sky et al., 2006], а также результаты расчетов.

• 1.1.    Краткое описание фотохимической модели

Уравнение неразрывности для химической примеси записывается в виде уравнения

∂µ+U ∂µ +V ∂µ+W∂µ=PAD-Lµ, ∂t    acos θ∂λ    a∂θ    ∂z где µ – отношение смеси какого-либо химического компонента, λ – долгота, θ – широта, z – высота, a – радиус Земли, РAD – фотохимические источники, L – характеристики фотохимических стоков; U, V и W – компоненты скорости в направлении λ, θ и z соответственно.

Для описания адвективного переноса в модели использована схема Пратера [Prather, 1986]. Для решения уравнения неразрывности по этой схеме (являющейся в существенной мере схемой Эйлера) его следует записать в потоковой (дивергентной) форме

∂ ( µρ ) ₊ ∂ ( U µρ ) ₊ ∂ ( V µρ cos θ ) ₊

∂ t    a cos θ∂λ     a cos θ∂θ

+∂(Wµρ)=PDI-Lµρ, ∂z где ρ=ρ0exp(–z/H) – плотность воздуха (ρ0 – плотность при давлении Р0; Н – высота однородной атмосферы; Р – давление и Р0=1013 мб) и РDI – фотохимические источники, записанные в дивергентной форме.

Очевидно, что обе формы уравнения переноса эквивалентны в случае, когда справедливо уравнение неразрывности

∂ ( U ρ ) ₊ ∂ ( V ρ cos θ ) ₊ ∂ ( W ρ ) _{= 0} a cos θ∂λ    a cos θ∂θ     ∂ z

Использование метода Пратера при тестовых расчетах показало, что ошибка этого метода по отношению к аналитическому решению не превышает 1 %, что на порядок меньше ошибки при использовании полулагранжевой cхемы. Следует добавить, что схема Пратера имеет третий порядок точности по пространству и первый по времени.

В данной модели был использован метод, основанный на идеологии «химических семейств», предложенный в работе [Turco, Whitten, 1974]. Как известно, система фотохимических уравнений является «жесткой» из-за большого диапазона времен жизни химических компонентов – от долей секунды до сотен лет. Химические «семейства» – искусственно введенные компоненты, время жизни которых значительно превышает время жизни компонентов, образующих соответствующее «семейство». Последнее обстоятельство во многом позволяет снять «жесткость» системы при решении фотохимической части системы уравнений и существенно увеличить шаг интегрирования по времени. Соответствующие химические «семейства» были выбраны следующим образом:

O х =O(¹D)+O(3P)+O 3 ,

HO х =H+OH+HO 2 +2H 2 O 2 ,

NO y =N+NO+NO 3 +2N 2 O 5 +HNO 3 +ClNO 3 , Cl y =Cl+ClO+HOCl+HCl+ClNO 3 .

Помимо химических компонентов, входящих в «семейства», модель содержит так называемые «ис-точниковые» газы: Н 2 , N 2 O, CH 4 , Н 2 О, Cl 4 , CF 2 Cl 2 ,

CFCl 3 , СН 3 Cl, O 2 . Кроме того, в модели задано вертикальное распределение концентрации молекул воздуха, которое определяет скорость реакций тройных соударений. Всего в фотохимическом блоке модели описывается взаимодействие между тридцатью химическими компонентами, участвующими в 73 газофазных химических реакциях и 38 реакциях фотодиссоциации. При решении уравнений переноса для химических «семейств» и газов-источников использовались фиксированные (не зависящие от времени) граничные условия. Шаг интегрирования по времени составлял 100 с, скорости диссоциации пересчитывались через один час модельного времени. Нижняя граница модели находилась на уровне земли, верхняя – на высоте 88 км, шаг по высоте был равен 2 км, шаг по широте – 5°, шаг по долготе – 10°. Начальные распределения всех малых газовых составляющих брались из одномерной фотохимической модели [Krivolutsky et al., 2005]. Глобальные поля компонент ветра и температуры предварительно рассчитывались по модели общей циркуляции [Krivolutsky et al., 2006]. При этом использовались соответствующие трехмерные поля, осредненные за сутки. На рис. 1 приведено глобальное распределение отношения смеси озона (ppbv) для января, рассчитанное по трехмерной фотохимической модели ЦАО.

• 1.2.    Модель глобальной циркуляции

  Модель является развитием одной из версий модели СОММА (Cologne Middle Atmosphere Model), разработанной в Институте метеорологии Университета Кельна, Германия [Jacobs et al., 1986]. Модифицированная версия САО/СОММА содержит более совершенные радиационные блоки (параметризации), учитывающие, в частности, перенос радиации в присутствии облачности и аэрозоля, а также имеет более детальное пространственное разрешение .

Исходная версия модели СОММА представляет собой глобальную механистическую сеточную модель на высотах от 2.7 до 135 км с высотным разрешением 5.7 км, широтным 10° и долготным 22.5°. Это позволяет разрешать волны с зональными волновыми числами до 8. В версии САО/СОММА шаг высотного разрешения составляет 1 км, а нижняя граница

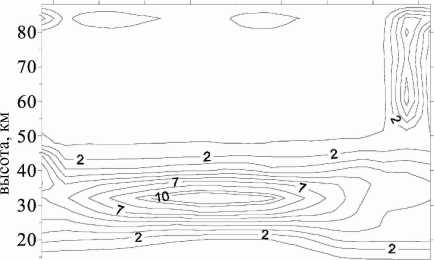
°-80 -60 -40 -20 0 20 40 60 80 широта

Рис . 1 . Глобальное распределение отношения смеси озона (ppmv) для января ( расчет по трехмерной фотохи мической модели ).

расположена на высоте ~1 км. Шаг по широте в интервале от –87.5° S до +87.5° N составляет 10°, шаг по долготе 11.25°. Верхний уровень лежит на высоте 135 км.

Модель основана на численном решении системы «примитивных» уравнений, записанных в сферических координатах (по вертикали используется лог – изобарическая высота):

∂ u ∂ t

1     ∂ ( u ² )

a cos ϑ ∂ϕ

( uv cos ϑ ) - a cos ϑ ∂ϑ

1 д , _х , и )        1 дФ

--^uw) + 1 f + “tg^ I^v--, p₀дz        V a )   a cos v дф

-Λ ϕϕ u + F u ^µ+ F u^D + G u ,

∂ v ∂ t

1   ∂uv acos ϑ ∂ϕ

( v ² cos ϑ ) - a cos ϑ ∂ϑ

∂

ρ ₀ - ∂ z

I         u1

( P o vw ) - I f +- tg v I u

V    a)

1 ∂Φ a - ∂ϑ

-Λ ϑϑ v + F v ^µ+ F v^D + G v ,

∂T       1   ∂uT     1

= -           -          ( vT cos ϑ ) -

∂ t    a cos ϑ ∂φ a cos ϑ ∂ϑ

- ^{1 ∂} ( ρ 0 wT ) - ^R wT -α ( T - T 0 ) +

ρ ₀ ∂ z         m c_pH

+ F ^µ + F + Q + G , T T i T ^,

1     ∂                1    ∂ u

(v cos ϑ) +          + acos ϑ ∂ϑ         acos ϑ ∂ϕ

1 ∂

+       ( ρ ₀ w ) = 0,

ρ ₀ ∂ z

∂Φ ₌ RT

∂ z m ′ H

где u – зональная скорость ветра (положительная на восток), v – меридиональная скорость ветра (поло-dz жительная на север), Т – температура, w = dt – вертикальная скорость (положительная вверх), Φ – геопотенциал, θ – широта, ϕ – долгота, f – параметр Кориолиса, z=Hln(p0/p), Н=7 км (высота однородной атмосферы), р0 – давление на фиксированной поверхности, р – давление, М – молекулярный вес воздуха, М0 – молекулярный вес на фиксированной поверхности, m =М/М0, а – радиус Земли, R – универсальная газовая постоянная, Т0 – температура основного состояния, зависящая только от высоты и широты, α – коэффициент ньютоновского выхолаживания, Γ – адиабатический градиент температуры, к – коэффициент молекулярной теплопроводности, Λmn – тензор ионного трения, µ – динамическая вязкость, ρ0 – плотность основного состояния, зависящая только от высоты, τ = Т/Т0, D – коэффициент турбулентной диффузии, Qi – источники и стоки тепла, Pr – число Прандтля, Gu, Gv – вклад гравитационных волн в изменение u, v, GT – вклад гравитационных волн в изменение Т.

Система уравнений (1)–(5) решается явным методом с фиксированным временным шагом 112.5 с.

Для предотвращения нелинейной неустойчивости за счет накопления энергии на малых (подсеточных) масштабах в модели применяется численная фильтрация. В процессе решения значение геопотенциала Φ рассчитывается из уравнения статики:

∂Φ ₌ RT

∂ z m ′ H

После интегрирования по высоте

Φ ( z ) = ^{R z T ( z )} dz .

H ₀ m ′ ( z )

Модель позволяет включать источник планетарных волн на поверхности Земли, задавая возмущение Φ 0 ( ϕ, θ ) либо по эмпирическим данным, либо в виде стилизованного волнового возмущения с заданными амплитудой, фазой, широтной структурой и зональным волновым числом.

Учет молекулярной вязкости в уравнениях для u и v производится в виде

1 m ′ ∂ m ′ ∂ u F_u ^µ =    ^{m m} µ ^u

ρ0 τ ∂z τ ∂z для зональной скорости и в виде

1 m ′ ∂ m ′ ∂ v

F ^µ =          µ

ρ 0 τ ∂ z τ ∂ z

для меридиональной скорости, где µ – динамическая вязкость.

Вклад турбулентности в изменение u , v описывается следующим образом:

F ^D u

для u и

F v^D

1 д ( _n Uu 1 ρ D

P _o д z C ⁰ д z )

1 д ( „д v 1 ρD p0 дz C 0 дz )

для v , где D – коэффициент турбулентной диффузии.

Вклады молекулярной и турбулентной теплопроводности в изменение температуры записываются в виде

µ

T ⁼

1 m ′ ∂ m ′ ∂ T k

ρ ₀ τ ∂ z τ   ∂ z

и

D

T

1 ∂ ρ ₀ Pr ∂ z

^ρ 0 ^D

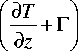
соответственно. Также учитывается ионное трение.

Входными параметрами для схемы учета воздействия ВГВ [Lindzen, 1981] в модели являются: горизонтальная длина волны l =200 км, вертикальные скорости на нижней границе для трех волн W =0.15, 0.02, 0.02 м/с. Фазовые скорости равны 0, 30, 60 м/с, азимуты – 0, 45, 135, 180, 225, 315°. С учетом приведенных параметров в схему включено восемнадцать волновых компонент.

В радиационных блоках модели САО/СОММА ниже высоты 60 км была использована более современная по сравнению с моделью СОММА параметризация выхолаживания в инфракрасной области

[Chou, 1994], позволяющая не только менять содержание углекислого газа в атмосфере, но и учитывать влияние облачности и аэрозоля (при заданном балле облачности и параметрах аэрозольных частиц). Выше 60 км использовалась параметризация выхолаживания СО 2 , учитывающая отклонение от локального термодинамического равновесия [Fomichev et al., 1998], что важно при расчетах температуры в верхней стратосфере, мезосфере и нижней термосфере.

Нагрев средней атмосферы, который учитывается в модели, происходит при поглощении солнечной радиации озоном в полосах Шаппюи, Хëггинса и Хартли и молекулярным кислородом в полосах Шумана–Рунге и континууме Шумана–Рунге. Ниже приводятся используемые параметризации [Strobel, 1978] скоростей нагрева (K/с) в соответствующих участках спектра:

полосы Шаппюи :

Q Ch / n (О з )=1.05 - 10"¹⁵ехр(-2.85 - 10"²¹ N 3 );

полосы Х ë ггинса :

Q Hu / n (O 3 )=1/ N 3 {4.66·10³–7.8·10²exp(–1.77·10^–19 N 3 )– –3.88·10³exp(–4.22·10^–18 N 3 )};

полосы Хартли :

Q Ha / n (O 3 )=4.8·10^–14exp(–8.8·10^–18 N 3 );

полосы Шумана – Рунге :

Q srb /п (O 2 )=1/(0.67 N 2 +3.44 - 10 9 N 21^{/ 2}) N 2 > 10¹⁸ см"²;

полосы Шумана – Рунге :

Q srb / n (O 2 )=2.43 - 10"¹⁹ N 2 < 10¹⁸ см"²;

континуум Шумана – Рунге :

QSRC/n(O2)=1/N2{0.98 exp(–2.9·10–19N2)– –0.55 exp(–1.7·10–18N2)–0.43 exp(–1.15·10–17N2)}, где n(O3), n(O2) – плотности частиц озона и молекулярного кислорода, го

N2 = j n(O2)dz / cos %, го

N ₃ = j n (O ₃ ) dz /cos % ,

• X - зенитный угол Солнца.

Было проведено сравнение результатов численного моделирования (среднемесячные данные) с моделью стандартной атмосферы CIRA’86. Модель достаточно хорошо воспроизводит глобальное среднезональное температурное поле, включая холодную летнюю мезосферу.

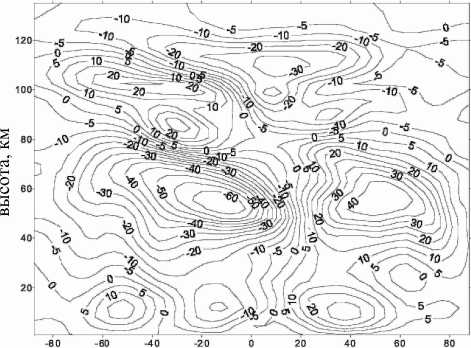
На рис. 2, 3 приведены глобальные распределения температуры и скорости зонального ветра (для января), рассчитанные по модели общей циркуляции.

• 1.3.    Воздействие энергичных частиц на состав , температуру и циркуляцию атмосферы

Ионизация атмосферы частицами высоких энергий приводит к дополнительному образованию азотных и водородных окислов. Следовательно, для моделирования такого типа воздействий и формирования дополнительных химических источников в соответствующем блоке модели необходимо предварительно рассчитать пространственно-временную структуру ионизации . Для расчетов ионизации в период

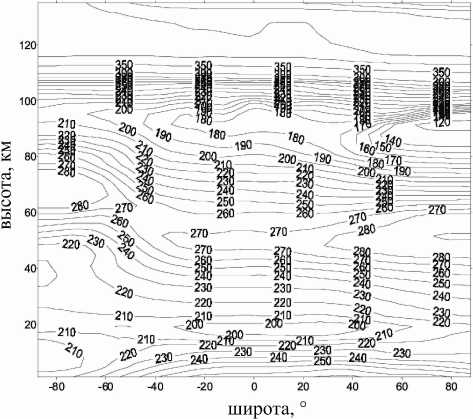
Рис . 2 . Глобальное распределение температуры (K) для января ( расчет по модели общей циркуляции ).

широта,

Рис . 3 . Глобальное распределение скорости зонального ветра ( м /c) для января ( расчет по модели общей циркуляции ).

геомагнитных возмущений октября и ноября 2003 г. был использован трехмерный модуль AIMOS [Wis-sing, Kallenrode, 2009], состоящий из двух частей: пакет GEANT4 и результаты наблюдений со спутников GOES (стационарная орбита) и POES (полярная орбита). По данным измерений потоков солнечных протонов и релятивистских высыпающихся электронов были рассчитаны скорости ионизации в атмосфере.

В работе [Криволуцкий и др., 2011] были представлены результаты расчетов (с помощью модуля AIMOS) скоростей ионизации атмосферы солнечными протонами для 28 октября 2003 г. В данной работе была показана незональность в распределении скоростей ионизации, обусловленная смещением магнитного полюса относительно географического, а также проникновением областей повышенной ионизации до более низких широт вследствие расширения полярных шапок в период геомагнитного возмущения. Последнее обстоятельство является важным, поскольку во всей области повышенной ионизации происходит, как было сказано выше, дополнительное образование окислов азота и водорода, разрушающих озон.

Рассчитанные суммарные скорости ионизации (протоны и электроны) позволяют, как уже говорилось, вычислять дополнительные химические источники в соответствующих уравнениях фотохимической модели. Наличие таких дополнительных источников трансформирует практически все компоненты, в первую очередь водородные, азотные и озон. Следует отметить, что период октября–ноября 2003 г., когда велись спутниковые наблюдения химического состава атмосферы прибором MIPAS, установленным на спутнике ENVISAT, лег в основу международного проекта НЕРРА (High Energetic Particle Precipitations in the Atmosphere). В рамках проекта было впервые проведено сравнение результатов модельных расчетов изменений химического состава полярной атмосферы в период геомагнитных возмущений октября и ноября 2003 г. с данными наблюдений прибором MIPAS, которое показало их достаточно хорошее соответствие [Funke et al., 2011]. В сравнении участвовало десять моделей, включая модели ЦАО.

В настоящей работе с помощью трехмерной фотохимической модели был реализован сценарий долговременного воздействия энергичных частиц на полярную озоносферу. Рассчитанные глобальные изменения озона, вызванные воздействием энергичных частиц, были заложены в модель общей циркуляции, что позволило получить соответствующий отклик температуры и ветра. В фотохимических расчетах были использованы расчеты скорости ионизации, обусловленной энергичными частицами, на основе модуля AIMOS с шагом по времени 2 ч. Уравнения модели интегрировались на год начиная с 26 октября календарного года. Ниже представлена разность результатов, полученных по сценарию с «возмущением» и сценарию без учета воздействия частиц (т. е. рисунки показывают только эффект воздействия энергичных частиц).

На рис. 4, 5 представлена эволюция изменений содержаний окислов азота (NO y ) и озона (в % по отношению к невозмущенному состоянию) для высоких широт Северного полушария (75° N). Видно, что, вследствие большого времени жизни «нечетного»

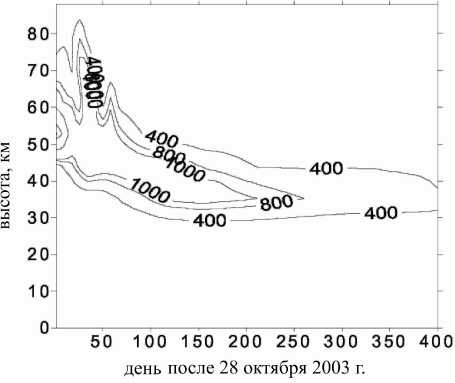
Рис . 4 . Эволюция возмущения в NO _y (%) после 28- го октября 2003 г . ( расчет по трехмерной фотохимической модели ).

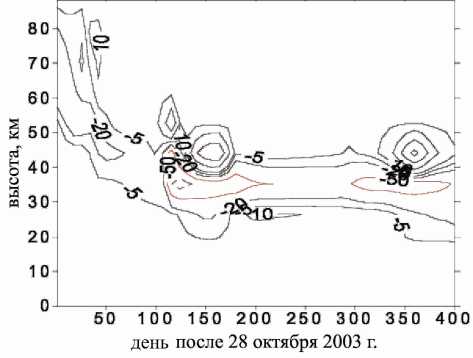
Рис . 5 . Эволюция возмущений в содержании озона (%) после 28- го октября 2003 г . ( расчет по трехмерной фото химической модели ).

азота, его воздействие на озон сказывается на протяжении всего года после сильных геомагнитных возмущений в октябре–ноябре 2003 г. и что воздействие на озон интенсифицируется после окончания полярной ночи.

Этот важный результат был заложен в радиационный блок модели общей циркуляции. Ниже представлены рассчитанные по модели общей циркуляции соответствующие изменения температуры и скорости зонального ветра, обусловленные изменениями содержания озона.

На рис. 6, 7 изображены изменения температуры для 75° N для всей области интегрирования по высоте и для нижней стратосферы и тропосферы. Наибольший эффект (охлаждение) наблюдается в летний период (высокий уровень солнечной радиации) в стратосфере. В то же время небольшие изменения температуры существуют и на тропосферных уровнях.

На рис. 8 показана широтная структура изменений температуры на высоте 37 км (квазистационар-ный по времени уровень разрушения озона). Рисунок наглядно демонстрирует различие в отклике температуры между северной и южной полярными областями, обусловленное различием в циркуляции в период сильного воздействия энергичных частиц (октябрь–ноябрь 2003 г.).

На рис. 9, 10 представлены соответствующие изменения абсолютных значений скорости зонального ветра для северной полярной области (75° N) в нижней тропосфере и стратосфере (рис. 9) и во всей области интегрирования (рис. 10). Из рисунков следует, что максимальные изменения (увеличение) скорости зонального ветра наблюдаются в весенний и осенний периоды в верхней стратосфере . В тропосфере в осенний период (спустя год после воздействия частиц) скорость зонального ветра ослаблена.

На рис. 11 изображены соответствующие изменения абсолютных значений зонального ветра в нижней стратосфере и тропосфере для южной полярной области (72.5° N): зональная циркуляция в этой области высот (в отличие от северной полярной области) практически невозмущена, что, необходимо подчеркнуть, является следствием сезонного

Ш1

t, день после 27.10.2003 г.

Рис . 6 . Долговременные изменения температуры (K) на 75° N, связанные с изменениями содержания озона , обусловленными воздействием энергичных частиц ( расчет по модели общей циркуляции ).

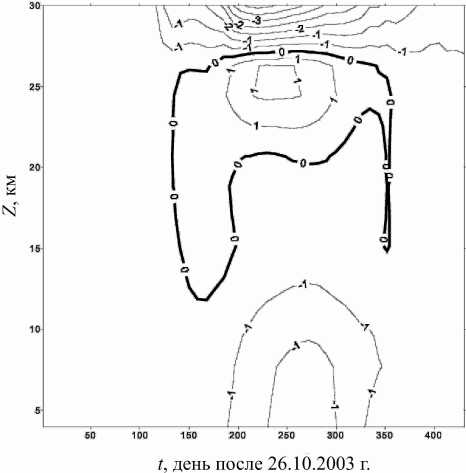
Рис . 7 . Изменения температуры (K) в тропосфере и нижней стратосфере на 75° N, связанные с изменениями содержания озона , обусловленными воздействием энер гичных частиц ( расчет по модели общей циркуляции ).

различия в циркуляции в период интенсивного воздействия частиц.

• 1.4.    Воздействие вариаций потока УФ - радиации Солнца

Двадцать третий цикл активности Солнца характеризовался не только затянувшимся минимумом, но и, как показали спутниковые наблюдения, необычайно низкими значениями потоков УФ-радиации.

С помощью модели общей циркуляции было реализовано два сценария: для максимума и для минимума активности Солнца (интегрирование на два модельных года). Изменение уровеня УФ-радиации между максимумом и минимумом активности Солнца задавалось примерно в соответствии с рис. 12

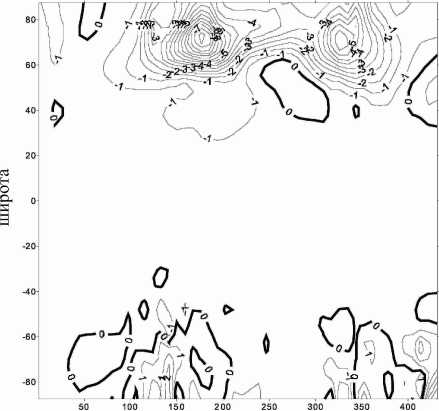
Z, день после 27.10.2003 г.

Рис . 8 . Изменения температуры (K) на высоте 37 км , связанные с изменениями содержания озона , обусловлен ными воздействием энергичных частиц ( расчет по модели общей циркуляции ).

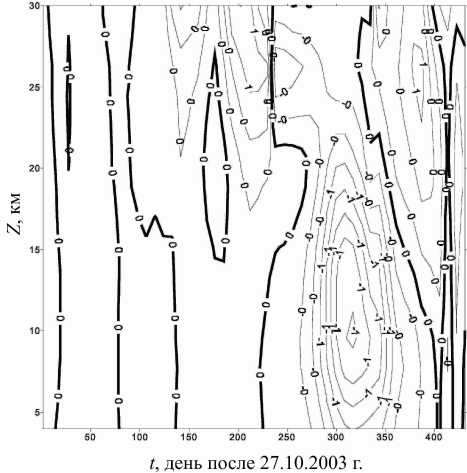
Рис . 9 . Соответствующие изменения абсолютных зна чений скорости зонального ветра ( м / с ) на 75° N в тропо сфере и нижней стратосфере ( расчет по модели общей циркуляции ).

(в зависимости от длины волны). В минимуме активности 23-го цикла уровень понижения УФ-радиации (%) брался примерно вдвое больше, чем в предыдущих циклах. Таким образом, в численных сценариях (в зависимости от длины волны) использовались следующие величины изменений (%) потока УФ-радиации Солнца между максимумом и минимумом активности 23-го цикла:

континуум Шумана–Рунге (<175 нм) 21; полосы Шумана–Рунге (175–200 нм) 15; континуум Герцберга (200–242 нм) 9; полосы Хартли (242–310 нм) 4.5;

полосы Хаггинса (310–400 нм) 3;

полосы Шаппюи (400–850 нм) 1.5.

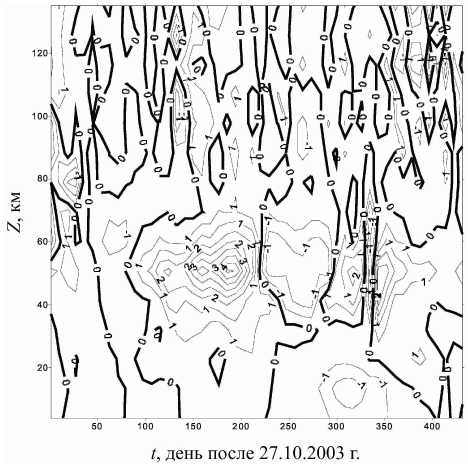
Рис . 10 . Изменения абсолютных значений скорости зо нального ветра ( м / с ) на 75° N в средней атмосфере и ниж ней термосфере ( расчет по модели общей циркуляции ).

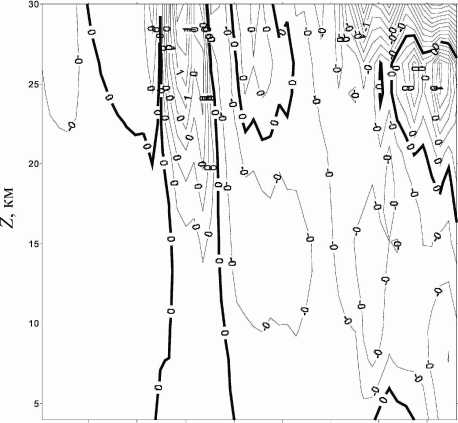
50      100      150      200      250      300      350      400

t, день после 27.10.2003 г.

Рис . 11 . Изменения абсолютных значений скорости зонального ветра ( м / с ) на 72.5° S в тропосфере и нижней стратосфере ( расчет по модели общей циркуляции ).

Эти вариации закладывались в радиационные блоки модели, учитывающие поглощение озоном и молекулярным кислородом.

При реализации численных сценариев, как уже говорилось выше, на нижней границе модели задавались амплитуды и волновые характеристики внутренних гравитационных и стационарных волн. Пространственная структура и их амплитуды на нижней границе модели в стилизованном виде соответствовали наблюдениям, включая годовой ход их амплитуд. Были включены стационарные возмущения с волновыми числами S =1, 2, 3. Ниже представлены результаты расчетов, характеризующие разности температур и скоростей зонального ветра в максимуме и минимуме активности. Приведены разности среднемесячных значений в конце каждого из двухлетних периодов интегрирования.

Х=164.5 нм

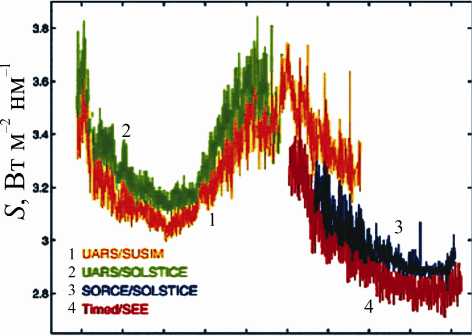
1992 1994 1996 1996 2000 2002 2004 2006 2006 2010

год

Рис . 12 . Вариации потока УФ - радиации Солнца на длине волны 164.5 нм по наблюдениям со спутников [Matthew et al., 2012].

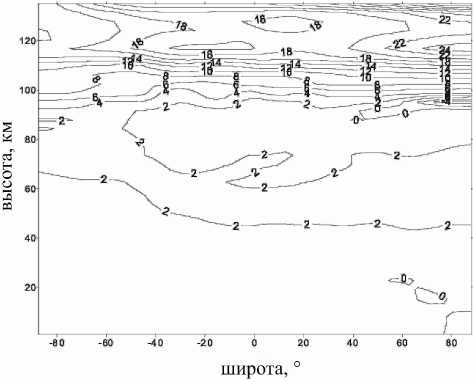
Рис . 13 . Изменения температуры (K) в цикле активно сти в июле ( расчет по модели общей циркуляции ).

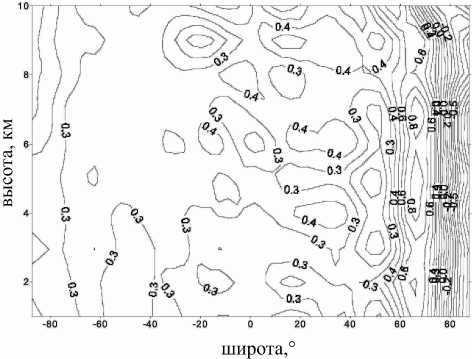
Рис . 14. Изменения температуры (K) в тропосфере в цик ле активности в июле ( расчет по модели общей циркуляции ).

На рис. 13, 14 представлены модельные изменения температуры в средней атмосфере и нижней термосфере, а также в нижней тропосфере для июля (рис. 14). Как показывает рис. 13, эффект солнечного цикла составляет порядка 2 K на высоте максимума озона и быстро увеличивается с высотой в ниж-

долгота,

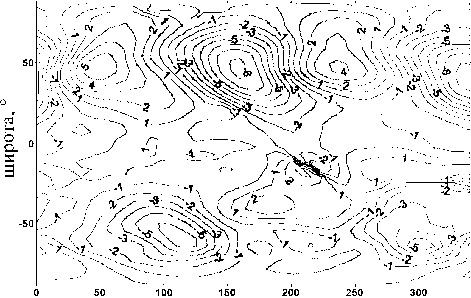
Рис . 16 . Изменения температуры (K) в тропосфере (5 км ) в цикле активности в июле ( расчет по модели общей цирку ляции ).

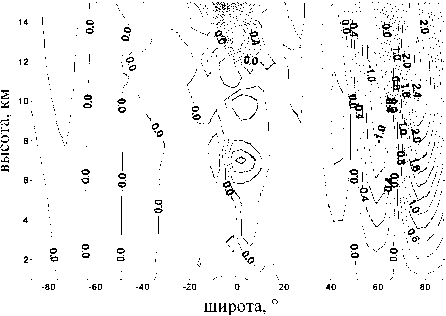
Рис . 17 . Изменения скорости зонального ветра ( м / с ) в тропосфере в июле в цикле активности ( расчет по модели общей циркуляции ).

долгота,

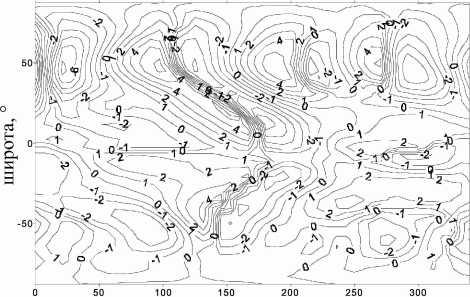
Рис . 15. Изменения температуры (K) в стратосфере (30 км ) в цикле активности в июле ( расчет по модели общей циркуляции ).

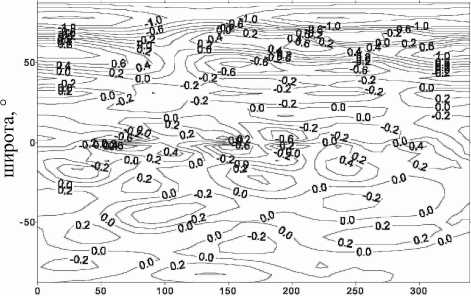
долгота,

Рис . 18 . Изменения скорости зонального ветра ( м / с ) в нижней тропосфере (5 км ) в июле в цикле активности ( расчет по модели общей циркуляции ).

ней термосфере, где амплитуда колебаний радиации, поглощаемой молекулярным кислородом, выше. Эффект в тропосфере (среднезональные величины) в июле выше над летним полюсом и составляет ~1 K.

На рис. 15, 16 изображены широтно-долготные разрезы изменений температуры для высот 30 и 5 км соответственно . Видно, что эффект солнечного цикла имеет волновую структуру (которая подавляется при осреднении по кругу широты) с амплитудой несколько кельвинов . Данная структура, очевидно, обусловлена наличием стационарных волн, по средством которых возмущение передается от высоких слоев атмосферы на уровне тропосферы и нижней стратосферы.

На рис . 17, 18 представлены соответствующие изменения скорости зонального ветра для июля. Видно , что зонально-осредненные величины этих изменений в июле выше над летней полярной областью и составляют около 1 м/c (рис . 17). На рис . 18 показан широтно-долготный разрез изменений скорости зонального ветра для высоты 5 км (июль). Вновь видна волновая структура с амплитудой более 1 м/c в северной полярной области.

Заключение

Представленные результаты численного моделирования могут служить основой для дальнейшего количественного анализа механизмов воздействия конкретных физических факторов – вариаций солнечной УФ-радиации и потоков частиц высоких энергий космического происхождения. Показано, что эффект воздействия корпускул на полярную атмосферу существенно зависит от циркуляции в период воздействия. В частности, образованные в результате такого воздействия окислы азота, имеющие большое время жизни, могут в условиях зимнего полярного вихря достичь уровней нижней стратосферы и вызвать дополнительное разрушение озона в этой области. Изменения содержания озона, в свою очередь, должны привести к изменениям ветра и температуры. Следует отметить, что этот эффект не реализуется летом вследствие наличия нисходящих движений над полюсом.

Аномально низкие уровни УФ-радиации Солнца в 23-м цикле солнечной активности увеличили размах этих колебаний, что привело к увеличению воздействия на атмосферу Земли посредством участия в этой цепи газов-поглотителей (озона и молекулярного кислорода), эволюция которых (их фоновые значения) в существенной мере может определять эффект. Представляется важным и наличие еще одного звена, связывающего верхнюю атмосферу с нижележащими слоями, – крупномасштабных атмосферных волн. В настоящей работе обнаружен сигнал в нижней атмосфере, имеющий волновую структуру и в значительной степени подавленный при осреднении вдоль круга широты. Представляется интересным продолжить работу в этом направлении, проведя исследования вклада солнечной актив- ности в глобальные и региональные изменения природной среды и климата.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 09-05-00949_а), в рамках участия в подпрограмме «Исследование и изучение Антарктики» ФЦП «Мировой океан» (контракт № 1-6-11 с ААНИИ Росгидромета), а также в интересах международного проекта “Study of Cosmic Rays Influence upon Atmospheric Processes” ISSI (International Space Science Institute).