Трехмерные предельно короткие оптические импульсы в фотонном кристалле на основе полимерной матрицы и углеродных нанотрубок

DOI:

Под фотонным кристаллом принято понимать нелинейную периодическую среду, с периодом порядка длины волны падающего излучения. Интерес к получению периодических структур на основе углеродных нанотрубок (далее – УНТ) возник в 1998 г., после выхода работ [13; 14; 18]. Там большие массивы выровненных УНТ были впервые изготовлены на подложках с использованием химического осаждения из паровой фазы, усиленного плазмой, где контролировались диаметр и длина каждой углеродной нанотрубки. Размещение и расположение нанотрубок осуществлялось с помощью электронно-лучевой литографии для создания рисунка никелевых точек, которые служат катализатором роста нанотрубок.

Для того, чтобы УНТ оставались в вертикальном положении и, для необходимой при построении фотонного кристалла, периодичности структуры подходит полимерная матрица, внутри которой помещены нанотрубки. Отметим, что углеродные нанотрубки совместно с полимерами, не только улучшают механические свойства материала, но и, например, повышают электропроводность, теплопроводность, теплостойкость и придают нанокомпозиту новые функциональные свойства. Отметим, что достаточно давно разработаны и запатентованы различные механизмы получения нанокомпозитов допированных углеродными нанотрубками [7; 8].

Интерес к коротковолновым импульсам фемтосекундной длительности не угасает уже последние несколько десятилетий [12; 15; 16], среди неопсоримых достоинств которых, особенно ценны следующие: энергия сосредоточена в ограниченной области пространства на протяжении длительного времени; высокая направленность излучения; стабильность формы и повышенная устойчивость к внешним возмущениям [4; 9; 17].

Нелинейные оптические среды на основе полимерной матрицы, допированной углеродными нанотрубками могут широко применяться для создания источников когерентного излучения, создания источников света с переменной частотой, полностью оптических линий задержки, полностью оптических буферов и т. д. [10].

Физическая модель и основные уравнения

Для решения поставленной задачи, при построении физической модели, использовались некоторые приближения, в частности, приближение сплошной среды; отсутствие учета электрического поля подложки; бесконечная длина УНТ (такое приближение справедливо, так как вертикальный геометрический размер импульса много меньше типичной длины нанотрубки); при решении трехмерной задачи, в силу цилиндрической симметрии, производной по углу можно пренебречь (это допустимо, так как эффект накопления заряда в какой-либо области не превышает 5 %).

Уравнения Максвелла, описывающие динамику вектор-потенциала трехмерного предельно короткого импульса, имеют вид [5; 6]:

. , n ²( z ) d ² A 4n . , 4n . , _n

AA 2—тут + — jcwT(A)+ — jp’oi(A) = 0,(1) cot c c где А – вектор-потенциал электрического поля коротковолнового импульса, n(z) задает периодический показатель преломления, т.е. фотонный кристалл, с – скорость света, jCNT – компонента плотности тока, описывающая УНТ, jPOL – компонента плотности тока, описывающая полимер.

Компонента для описания плотности тока полупроводниковых УНТ, была получена, например, в работе [3] и имеет вид:

^jCNT = e E ^Vs ⁽ p ) l p - e A ⁽ t ) к C Ps C ps },    (2)

ps V c )

где e – заряд электрона, p – квазиимпульс электрона, t - время, C^ s , C_ps - операторы рождения и уничтожения электронов с квазиимпульсом (p, s) ;

– усреднение с неравновесной матрицей плотности с(t) . Слагаемое v_s(p) представляет собой групповую скорость электронов и имеет вид [3]:

I S (p) 1 exPI- Yт | bq =E asq Jcos(apq)Г Bq    ' dp, s=1 ZB             1 , I S (p) I          (6)

ZB        1 + exp<^ — s¹^

I kBT J где ZB – первая зона Бриллюэна; asq – коэффициенты разложения закона дисперсии электронов [11] в ряд Фурье; kB – постоянная Больцмана; T – температура.

Начальное условие на вектор-потенциал электрического поля импульса выбиралось в виде Гаусса и имеет вид:

V s ( p ) =

6 s s ( p ) 5 p

A t =o

= A о exp

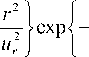
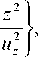
s s ( p ) = ± y 0 ( 1 + 4cos( ap )cos( ns An )

+ cos²

(3) (ns(m )Y 2 ,

где г 0 - интеграл перекрывания ( « 2.7 эВ), а - постоянная решетки УНТ, m – количество гексагонов по периметру нанотрубки.

dA 2Vz I r21 I z2 — = — Ao exP|—2 Г exP|—2 dt u u u t=o z r 1 J V z

Выражение, описывающее плотность тока полимерной матрицы, можно описать по аналогии с системой квантовых точек с прыжковой проводимостью [1]. Принимая во внимание выесказанное выражение для j _Pol будет иметь вид:

jpoi = e E V ⁽ p ) ( p - e^{A (} t ) ^C + C-- к (4) pS G V c )

где u_r , u_z – параметры, определяющие ширину импульса вдоль осей z и r , соответственно; А₀ – начальная амплитуда импульса; V – скорость входа импульса в массив ориентированных УНТ.

Эффективное уравнение (5) решалось численно, при помощи явной конечно-разностной схемы типа «крест», на равномерной сетке по времени и координате, со вторым порядком погрешности [2].

Отметим, что вектор-потенциал электрического поля импульса связан с его напряженностью посредствам калибровки Кулона:

Выражения для компонент плотности тока нанотрубок (2) и полимерной матрицы (4), подставим в волновое уравнение и получим эффективное уравнение на вектор-потенциал электрического поля трехмерного предельно короткого оптического импульса, распространяющегося в нелинейной среде фотонного кристалла:

E =

dA cd t ’

а квадрат напряженности электрического поля импульса пропорционален его интенсивности.

, . n ²( z ) d ² A  4 en_rNT(qaeA A

AA --—_r +-- — > qb sin l  ---I +

q cdt       c q V c )

4 en_Po, . (a_PoleA A _n             ⁽⁵⁾

+-----Pol- sinl -PolI = 0, c V c )

здесь n _CNT – концентрация электронов в нанотрубках; n _Pol – концентрация полимера в фотонном кристалле; a _Pol - длина связи в полимере; A - лапласиан в цилиндрической системе координат. Отметим, что коэффициенты b_q имеют следующий вид:

Резул ьтаты

Временная эволюция напряженности трехмерного предельно короткого импульса при его распространении в фотонном кристалле на основе полимерной матрицы, допирован-ной УНТ, представлена на рисунке 1. Параметры показателя преломления фотонного кристалла следующие: глубина модуляции показателя преломления – 0.25, период модуляции – 100 мкм; скорость входа импульса в фотонный кристалл – 0.93 с .

При временной эволюции напряженности электрического поля происходят существенные изменения формы огибающей импульса, однако, его энергия остается сосредоточенной в ограниченной пространственной области. Амплитуда импульса практически не претерпевает изменений с течением времени.

Далее показана зависимость срезов интегральной интенсивности электрического поля импульса от координаты, в различные моменты времени (рис. 2).

Исходя из рисунка 2 можно сказать, что интегральная интенсивность растет с течением времени, что имеет важное значение, например, для скорости фотоионизации электро-

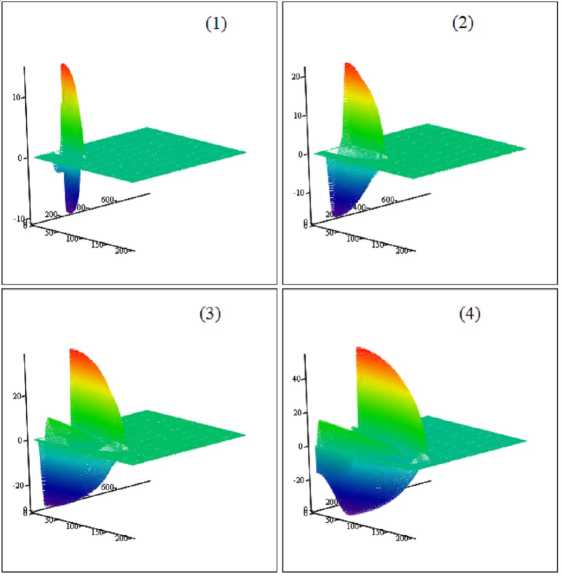
Рис. 1. Зависимость напряженности электрического поля импульса в фотонном кристалле из полимерной матрицы с УНТ в фиксированные моменты времени: ( 1 ) 5 пс, ( 2 ) 10 пс, ( 3 ) 15 пс, ( 4 ) 20 пс. По горизонтальным осям отложены координаты в мкм, по вертикальной оси отложена напряженность в В/мкм

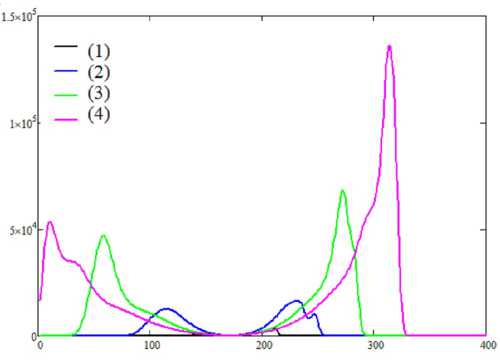
Рис. 2. Продольные срезы интегральной интенсивности электрического поля импульса в фотонном кристалле из полимерной матрицы с УНТ в фиксированные моменты времени: ( 1 ) 5 пс, ( 2 ) 10 пс, ( 3 ) 15 пс, ( 4 ) 20 пс. По горизонтальной оси отложена координата в мкм, по вертикальной оси отложена интенсивность в отн. ед.

нов в фотонном кристалле. Следует заметить, что импульс испытывает дисперсионное расплывание с течением времени.

Следующие результаты касаются зависимости свойств импульса от параметров модуляции показателя преломления фотонного кристалла (глубины и периода) и показаны на рисунке 3.

Влияние глубины модуляции показателя преломления фотонного кристалла сказывается на групповой скорости волнового пакета (с увеличением глубины модуляции групповая скорость падает) и его амплитуде (рис. 3, 1). Период модуляции показателя преломления также оказывает влияние на групповую скорость импульса, увеличивая ее (рис. 3, 2).

Поведение импульса при различных соотношениях концентрации полимера и УНТ в фотонном кристалле показано на рисунке 4.

Из представленного рисунка 4 видно, что увеличение концетрации полимера в фотонном кристалле приводит к усилению импульса, т.е. его амплитуда увеличивается, а форма огибающей сужается. Таким образом, фотонный кристалл на основе полимерной матрицы и углеродных нанотрубок может служить устройством для усиления фемтосекундных предельно коротких импульсов.

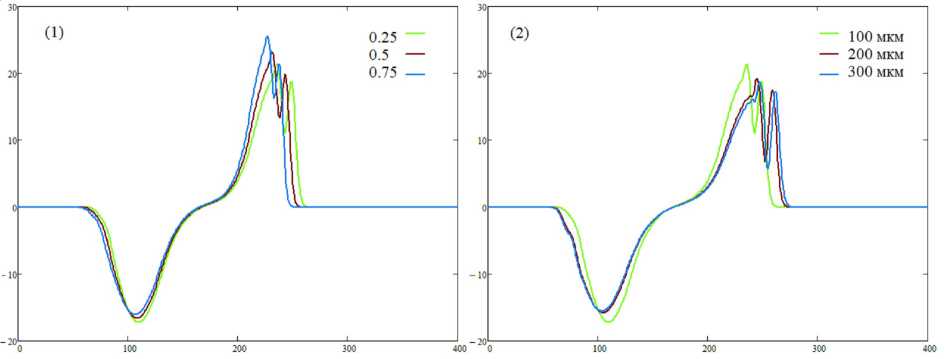
Рис. 3. Продольные срезы напряженности электрического поля импульса от координаты при его распространении в фотонном кристалле на основе полимерной матрицы и УНТ, в момент времени 10 пс, при различных значениях глубины модуляции показателя преломления (1) и периода модуляции показателя преломления (2). По горизонтальной оси отложена координата в мкм, по вертикальной оси отложена напряженность в В/мкм

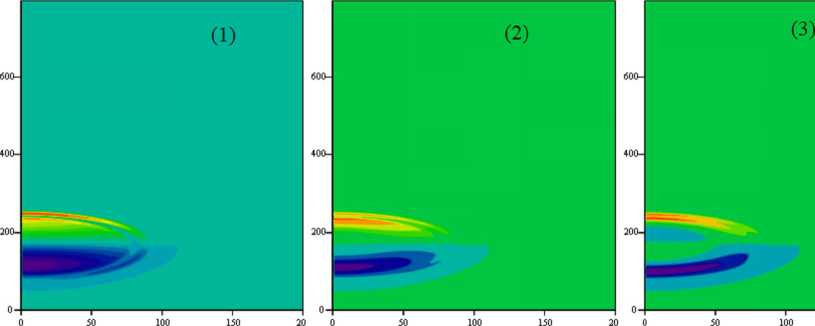
Рис. 4. Картины напряженности электрического поля импульса при его распространении в фотонном кристалле на основе полимерной матрицы и УНТ, в момент времени 10 пс, при различных значениях концентрации полимера и УНТ: ( 1 ) 1:2, ( 2 ) 1:1, ( 3 ) 2:1. По осям отложены координаты в мкм, цветовая шкала отражает напряженность

Выводы

Проведенное исследование динамики трехмерного предельно короткого оптического импульса в нелинейной среде фотонного кристалла на основе полимерной матрицы, допированной углеродными нанотрубками, показало, что:

• 1.    Присутствие полимера в фотонном кристалле усиливает предельно короткий импульс.

• 2.    Параметры модуляции показателя преломления фотонного кристалла оказывают существенное влияние на время задержки импульса, позволяя контролировать ее.