Трехмерные симметричные бифокальные системы

ТРЕХМЕРНЫЕ СИММЕТРИЧНЫЕ БИФОКАЛЬНЫЕ СИСТЕМЫ

Зеркальные системы, поверхности которых отличны от сферических, позволяют получить новые эффекты, недоступные оптическим системам со сферическими поверхностями. Асферические поверхности, точность изготовления которых определяется длиной волны, нашли пока применение в относительно длинноволновом диапазоне (сантиметровые - субмиллиметровые волны). Для данного диапазона длин волн применение станков с числовым программным управлением обеспечивает необходимую точность воспроизведения асферических поверхностей.

Одной из перспективных систем, которая в настоящее время усиленно разрабатывается [1], является бифокальная система, в которой аберрации точно устранены для двух направлений плоских волн. Бифокальные системы обладают меньшими аберрациями по сравнению с известными ранее системами при одном и том же количестве отражающих (преломляющих) поверхностей. Кроме того, бифокальные системы имеют в Зт5 раз больший угол обзора, чем зеркальные системы типа Кассегрена и Шварцшильда [2] . Хотя любая бифокальная система является трехмерной, первоначально теория бифокальных систем строилась как двумерная [3,4].

В [4] предлагалось решать двумерную задачу, а затем трактовать найденные профили как образующие осесимметричных зеркал. Очевидно, что указанное решение обладает аберрациями, даже для двух заданных направлений безаберрационной фокусировки. Более последовательно схема расчета трехмерных бифокальных систем была изложена в [5] , где был указан способ перехода от двумерной задачи к трехмерной.

Ниже для построения трехмерных бифокальных систем предлагается другой метод расчета. Преимущество данного алгоритма заключается в том, что он допускает анализ зависимости получающегося решения от исходных параметров системы и позволяет, варьируя исходные параметры, придать системе желаемые.свойства (например, добиться того, чтобы одно из зеркал было телом вращения).

Целью данной работы является синтез двух отражающих поверхностей, преобразующих две сферические волны, исходящие из двух фокальных точек, в две плоские волны. Расчет зеркальных поверхностей производится в приближении геометрической оптики, используя закон зеркального отражения и закон постоянства длины оптического пути (закон Малуса). Если задано положение фокальной точки rF, направление плоской волны п, а так- же длина оптического пути S от фокуса до плоского фронта, то существует взаимно однозначное соответствие между точками обоих зеркал и направлениями нормалей к поверхностям зеркал в данных точках. Действительно, если задана одна из точек на одном из зеркал г и нормаль к поверхности в данной точке v (рис. 1), то соответствующая точка на другом зеркале R и направление нормали в ней N определяются из соотношений:

R = г + К{8 - |г - rp| (1 - пр)}/(1 - nk);                        (1)

N = (n - k)/(2(l - пк)}1/з ,                                         (2)

где р = (г - rF)/|r - Гр|, к = р - 2v(v р) , а положение плоского фронта выбрано так, чтобы он проходил через фокальную точку. Если же задана одна из точек другого зеркала R и направление нормали к поверхности N в этой точке (рис. 2), то соответствующая ей точка первого зеркала г* и нормаль к поверхности V* определяются из соотношений:

г* = R + е L;

V' = (q - е)/{2(1 - qe)}72 , где е = 2N(N п’) - п';

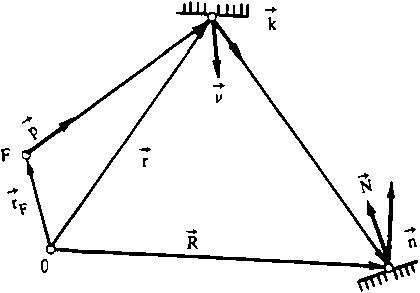
Рис. 1

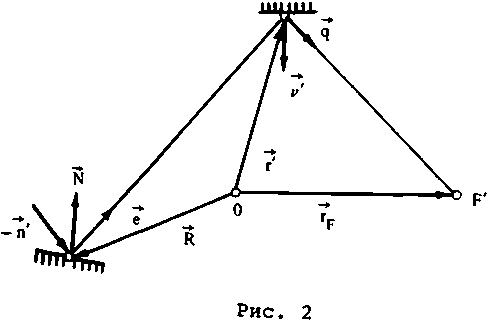
L = 0,5{(S' + n'(R - r£))2 - (R - r£)2}/

{S' + (e + n') (R - r^J} ;                                                  (6)

q = -(eL + R - r^)/ (S' - L + n' (R - r£)}.                         (7)

При совпадении пип' и r^ и Ер выражения для г* и v*, определяемые соотношениями (3)-(7), совпадают с г и у из (1) , (2). В противном случае г* и v¹ будут отличны от г и v при одних и тех же значениях R и N. Затем, используя (1),(2), можно определить R' и N', соответствующие г' и у*. По такой схеме проводится расчет бифокальных систем, так как для этих систем положения фокусов и направления нормалей к плоским фронтам различны. Для начала процедуры необходимо задать произвольно начальную точку на одном из зеркал го и направление нормали к поверхности зеркала в данной точке v₀- Далее, используя последовательно формулы (1) , (2) и (3)-(7), получим некоторую привилегированную систему точек, которую называют опорными точками. При произвольном задании фокусов F и F', нормалей к плоским фронтам, длин оптических путей S и S', начальной точки г₀ и нормали к•поверхности в этой точке v₀ получается несимметричная система опорных точек. Для того чтобы получить симметричную систему, необходимо начальные условия задать специальным образом.

Потребуем, чтобы система имела две плоскости симметрии. Две фокальные точки разместим симметрично одной из плоскостей, единичные векторы нормалей к плоским фронтам - симметрично другой из плоскостей, причем таким образом, чтобы фокальные точки и нормали к фронтам лежали в одной плоскости. Введем декартову прямоугольную систему координат так, как показано на рис. 3. В этой системе координат фокальные точки лежат на оси 0Y, а векторы нормалей к плоским фронтам задаются компонентами п+ = (0, -sin a, cos а} ; п_ = [0, sin а, cos а) .                 (8)

Начальную точку 0+ выберем таким образом, чтобы она лежала в плоскости XOZ и вектор нормали к поверхности зеркала в этой точке также лежал в данной плоскости, причем точка 0+ не должна лежать на оси OZ. Из требования симметрии точке 0"*" должна соответствовать точка О^-, симметричная точке О⁴ относительно плоскости YOZ. Очевидно, что расстояния от фокальных точек F_ и F₊ до точек О⁴ и О^- одинаковы. Будем характеризовать это расстояние параметром R_o. Затем введем два угла ф и ф (см. рис. 3) . Угол ф характеризует меру близости фокальных точек F+ и F_ к плоскости XOZ, а угол ф характеризует меру близости точек 0⁺ и 0“ к плоскости YOZ. Задание трех параметров R_o, Ф и ф определяет положение фокусов и начальных точек

F+ = Ro sin ф, F_ = -Ro sin ф, z„ = Ro cos ф cos ф, Уо = 0, Xq = Ro cos ф sin Ф,

—                                 • I                                    (9)

zo = Ro COS ф COS ф, У о = 0, xo = “Ro cos ф sin ф.

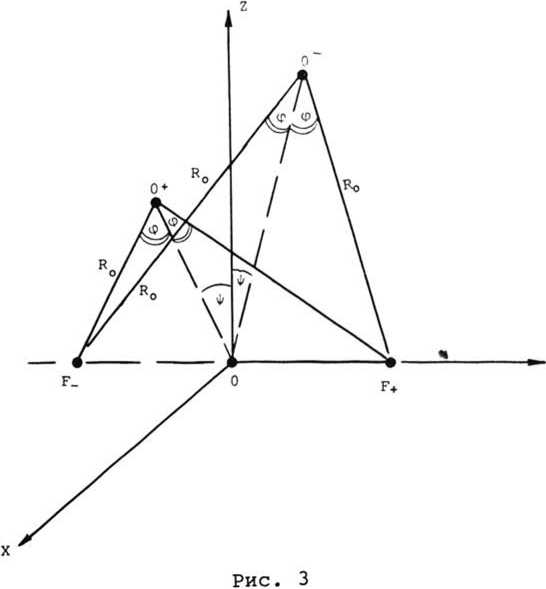
Как уже отмечалось выше, нормаль к поверхности в точке 0"*", а следовательно, и в точке 0“ должна лежать в плоскости XOZ, и поэтому единичный вектор нормали в начальной точке можно характеризовать одним углом. В качестве этого угла будем выбирать угол и между нормалью и положительным направлением оси ОХ. Тогда векторы нормалей в начальных точках можно записать в виде

= {-cos и, 0, -sin и}; Vg = {cos и, 0, -sin и}.(1°)

Как было показано выше, точке 0+ должна соответствовать точка 1 на другом зеркале. Относительную близость точки 1+ к плоскости XOY будем характеризовать параметром

Т = Z5/(Зф - 2*).(11)

Соотношение (11) определяет z-координату опорной точки 1⁺ через Zq и параметр т:

z; = (1 - i/x)z*.(12)

Из (1) , (2) и (12) определяются координаты первой опорной точки, направление нормали к поверхности в первой опорной точке 1"*" и длина оптического пути. Аналогично определяются три другие точки на большом зеркале I-, -1+ и -I- и направления нормалей к поверхности в этих точках. Эти точки симметричны точке 1 + относительно плоскостей YOZ и XOZ. Далее, используя формулы (3)-(7) и (1) , (2), последовательно можно получить сколь угодно много опорных точек. Так как реально система должна иметь конечные размеры, то число опорных точек должно быть ограничено.

Количество опорных точек будем характеризовать параметром J, который определяет максимальное число точек на каждом из зеркал.

Таким образом, задание одного размерного параметра R_o и шести безразмерных - а, ф, ф, и, т, J - однозначно определяет пространственную систему опорных точек на каждом из зеркал и направления нормалей в этих точках.

Построенную систему дискретных опорных точек необходимо связать с двумя непрерывными поверхностями, имеющими непрерывные производные первого порядка в каждой точке данной поверхности. Для этого необходимо задать некоторую поверхность между четырьмя соседними опорными точками так, чтобы данная поверхность проходила через данные точки и имела нормали, равные нормалям в данных точках. Из соображения симметрии в качестве данных опорных точек целесообразно взять точки 1+, 1", -1 + и -I-. Эти точки и нормали в них попарно лежат в плоскостях, расположенных симметрично относительно главных плоскостей симметрии. В качестве поверхности выберем поверхность параболоида, ограниченную плоскостями

Z = 21Г

(z - z^N^- (у - y^N^ = О,

(х - x^N^ - (z - z;)N*± = О и имеющую в точках ±1^ соответствующие нормали

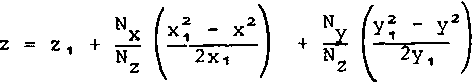
где х, , у, , zt - координаты точки 1 , a Nx, Ny, Nz - направляющие косинусы нормали в ней.

Если поверхность (14) определена, то, используя процедуру, описанную формулами (1)-(7), можно пересчитать эту поверхность в любую из областей, ограниченную четырьмя соседними опорными точками, причем получившиеся поверхности зеркал будут всюду непрерывны вместе со своими первыми проивводными.

Особый интерес представляет случай, когда J = 1, то есть цикл необходимо выполнить один раз. Другими словами, к зеркалу (14) необходимо рассчитать корректирующее зеркало. В этом случае большое зеркало может быть параболоидом вращения, если будет выполнено условие

Х1|у, = Nx|Ny.                                                        (15)

Выражая координаты и проекции нормали в первой опорной точке через параметры системы, получаем условие т sin ф = sin а[т + ctg Ф tg(2u + Ф) ] •                            (16)

Условие (16) определяет связь между параметрами системы и означает, что большое зеркало может быть телом вращения только в том случае, если уравнение (16) имеет решение.