Трехмодовое взаимодействие и нелинейное усиление оптических сигналов в световодах

Широко разрабатываемая в последние годы проблема создания оптического компьютера требует прежде всего построения его элементной базы: генераторов сверхкоротких световых импульсов, усилителей, полного набора логических устройств и т. д. К числу наиболее перспективных физических эффектов, используемых для этих целей, следует отнести нелинейные оптические явления в волоконных световодах. Такие явления характеризуются низким уровнем потерь, широкой полосой пропускания и возможностью получения больших интенсивностей, необходимых для проявления нелинейных эффектов при относительно малых значениях мощности.

Элементы оптического компьютера должны удовлетворять ряду таких существенных требований, как независимость результата работы от фазы входного импульса, неизменность частоты логических сигналов, устойчивость к флуктуациям и т. д. Средн широкого спектра нелинейных волоконных устройств лишь небольшая часть удовлетворяет таким требованиям. В настоящей работе для построения оптического усилителя предлагается использовать эффект параметрического взаимодействия трех мод. Отличительная черта такого устройства - независимость его усиления от фаз входных сигналов.

Общая теория нелинейного взаимодействия коротких импульсов в многомодовых световодах подробно разработана и конкретизируется в рамках следующих предположений:

• 1)    опущены все нестационарные составляющие (связанные как с дисперсией, так и с инерцией нелинейности) ;

• 2)    не учитывается влияние поглощения;

• 3)    не учитываются характерные для тонких волноводов эффекты, пропорциональные (Х/а)², где X - длина волны, а - поперечный масштаб (здесь следует отметить, что в уравнениях эволюции для ТЕ — распределений поля подобные слагаемые автоматически исчезают независимо от величины Х/а);

• 4)    высота поперечного профиля показателя преломления п(г) предполагается малой (модель слабонаправляющего волновода). При этом в амплитудах всех функций (но не в фазах!) пренебрегается различием волновых векторов k_m, т. е. полагается k_t = k₂ ~ о> n/с, где ш - частота волны.

• 5)    игнорируется влияние слагаемых, не удовлетворяющих фазовому синхронизму.

Пусть в световоде с продольной осью z распространяется трехмодовый волновой пакет, электрическое поле которого записывается в виде:

• ^1 = ^Re l^fo ' „S ₃^f_m (z) • %£ (fy • exp (ik_m z - iwt)] ,                                                 (1)

где ^m (z) — безразмерные комплексные амплитуды; e^ — нормированные модовые векторы поперечных распределений: < | е^ 12>= 1 (для осесимметричной структуры волновода <А> = J 2irR dR A, R = г/а, а - радиус световода) . Далее наложим требование синхронизации мод: kj + k3 = 2 • k2. Тогда в рамках указанных допущений уравнения эволюции модовых амплитуд f примут согласно [1, 21 вид' df.

"аГ = ь (Rn l^^ + Ru Ifz^+Ru '^ViRol"^, df2               1           ,                                                                                    (2)

It "‘^l lfl^+R22 lf2p + R23 ifa^ fi* ZiRo-qf;^.

dL           ,

• = i (R₃1 'fl I² * R₃2 ^lf2¹² * R33 ^lf3 f²) • f₃ * iR₀ ■ <1 fl

Здесь $ = z/L^. где L^ —длина нелинейного самовоздействия. Пропорциональные R_o слагаемые играют ключевую роль в дальнейшем рассмотрении. Их появление возможно лишь при выполнении указанной синхронизации мод. Далее используем простейшую модель нелинейного отклика показателя преломления: 8п_п| = n₂- I = с • e_Q • п • п₂ (^ 5), где I - вектор Пойнтинга, [п₂] = м²/Вт. Тогда 1/L_nl = -^ • (п₂ • Q/lf$ I²) • u₍ ^а², где Q = / 2nrdr I® - интегральная мощность нормирующей моды на входе в световод (Вт) (далее - это мощность накачки (2 мода)), |1q| - соответствующая этой моде входная амплитуда: fk * ₀⁼ 1^1^{- ех}Р Gv’k), (^ - начальные фазы); R_mn = u_mn/u_]1, ^Ro ^{= u}0^/ull-

Umm ~ 2   < ^ml^ > > um^=n ~ <'emJ " lenj + 2 (%ц " enp2 >>

• ^U0 ⁼<^11' ^e2p ' ^1 ■ ^e3p ⁺ ~ l®21l² " (®11 ' «31» •

Указанные соотношения полезно конкретизировать для двух типов профиля показателя преломления п(г):

• 1.    Параболический - п = п_с • (1 - Д - R²). 2. Ступенчатый - п = п_с при IRI < 1 и п = п , при IR| > 1; при этом п_с и п_с1 соответствуют показателям преломления сердцевины и оболочки, Д = (п_£ - п_с|)/п_с « 1 - высота профиля. Для параболического профиля можно выбрать азимутальные Лагерровы моды - ТЕ_{0102 03}: е₍ = = (VR/Vir) • exp (-VR²/2), е^= (VR/V2n) • (2 - VR²) - exp (-VR²/2), e₃ = (VR/x/Зя) • (3 - 3VR² + V² R⁴/2) x x exp (-VR²/2), где k² = "^2" " ⁿc ” -^' ^m- V = a - ш ■ n_c ■ V2A/c. Тогда 1/L_n| = (Зях/Д ■ n₂ - Q/ I f° I² )/(V2 x x n_c • a • X²), где X = 2 nc/(w • n_c) -длина волны. При этом R_]2⁼ L ^Riз ^{= R}23 ^{= 3}/^{4> R}22 ^{= 5}/⁸- ^R33 ^{= 15}/³²> R₀=V3/8.

Для реальных профилей показателя преломления (со скачком между сердцевиной и оболочкой) поиск мод, имеющих на одной частоте точки фазового синхронизма (kj + k₃ = 2 • k₂), требует определенных усилий. В настоящей работе мы рассматриваем четырехволновой параметрический процесс вида: 2ы₂ = Ш] + w₃; 2k₂ = к] + к₃. где Wj — частота, a k_f — постоянная распространения i-й моды. В оптических волокнах выполнение этих условий для данного набора взаимодействующих мод обычно достигается за счет компенсации материальной дисперсии - межмодовой при определенных значениях отстройки |Ш] - ы₂1 = |ц>₃ - о>₄1 В то время как для усилителя разнесение частот накачки и сигнала может являться даже более предпочтительным (для избежания перекрестных помех), работа логических устройств требует одночастотного взаимодействия. В этом случае для выполнения условия синхронизма необходим специальный подбор мод и параметров световода. Заметим, что в объемных средах аналог такого одночастотного взаимодействия отсутствует, поскольку при неколлинеарном взаимодействии условие синхронизма: 21^ = 1^ + ?₃ , где k, = к₂ = к₃ невыполнимо. В данной работе было проведено численное исследование характеристических уравнений низших мод для ступенчатого профиля показателя преломления. При этом для Д= 0,001 можно привести пример точки синхронизма: мода 1 - четная НЕ^, мода 2 - четная НЕ^- мода 3 — четная НЕ^, V = 12,01. Расчет соответствующих интегралов перекрытия дает: u, ₃ = 0,5548, R_H = 1, R_J2 = R_2| = = 0,9352, R|₃ = R₃₁ = 1,6614, R₂₂ = 0,8384, R₂₃ =R₃₂ =0,6642, R₃₃ = 1,538, R_Q = 0,2654.

Аналитическое решение системы (2) основано на энергетических интегралах: 2W( + W2 = D] = const; 2W3 + + W- = D, = const, где W = I f I2 - интенсивности мод. При этом (2) удается довести до квадратур Якоби:

dW2 "dT

= 4Rq W² - (D, - W₂) - (D₃ - W₂) - (AW² + BW₂ + C)²,

A = -J- (2R,2 - R„ - R13 + 2R21 - 4R,2 + 2R23 + 2R32 - R31 - R„),

B= -^ (R„ -2Rn+R31)+ -y-(R13 - 2R23 + R33).                                      (4)

C = 4R_q VW_1OW²_O.W_3O • cos (_Ло - 2^,0 + ^₃₀) - A • W²₀ - В ■ W_2Q.

Периодические решения (4) выражаются через эллиптические функции, выписывать которые здесь нецелесообразно. Отметим лишь важнейшие для прикладных задач свойства системы (2), вытекающие из представления (4):

• 1)    если W₃₀ = 0, то эволюция амплитуд не зависит (!) от начальных фаз сигнала и накачки (1 и 2 моды). Актуальность данного утверждения отмечена выше;

• 2)    отсутствие на входе сигнальной моды (W_J0 = 0) означает ее отсутствие по всей длине световода (если при этом и W_3Q = 0).

Результаты численного интегрирования системы (2) продемонстрированы на рис. 1. При этом матрица коэффициентов соответствовала упоминавшимся выше азимутальным ТЕ0П модам Лагерра для параболического про-

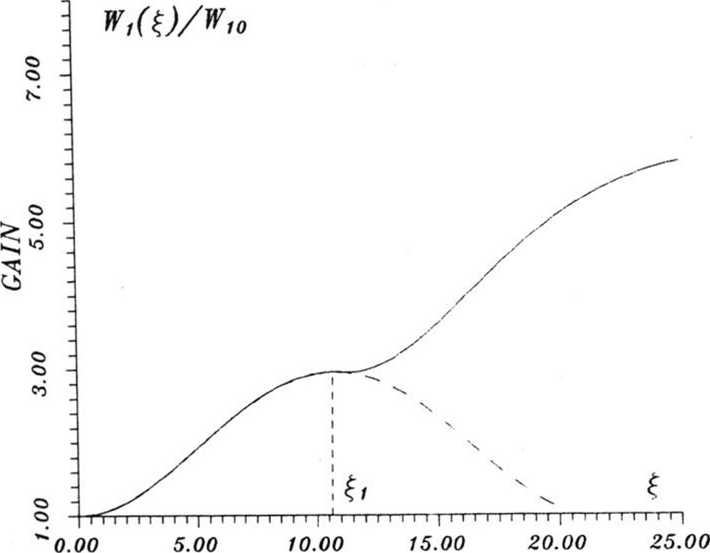
DISTANCE

Рис. 1. Коэффициент усиления сигнальной моды по длине при W2Q = 1, W30 = 0. До т. 5] -1-й каскад. При £ > ^ -либо без подавления 3-й моды (пунктирная кривая), либо с дискретным подавлением ее на коротком участке (сплошная кривая второго каскада)

филя п(г). Предполагалось, что на входе ({ = 0) задана единичная мода накачки (W20 = 1) и слабый сигнал (W10 = = 0,1), рост которого по длине обусловлен возникающей 3-й модой. После достижения максимума в т.^ сигнальная мода должна убывать (пунктирное продолжение), что обусловлено вредным (на данном этапе) воздействием накопившейся 3-й моды. Новый рост W( после точки ^ несложно обеспечить, подавив 3-ю моду. Технологически это можно осуществить, сузив на коротком расстоянии световод до радиуса, переводящего 3-ю моду в вытекающую (за условие отсечки). Расширив после этого волновод до прежнего радиуса, получим второй каскад усиления сигнальной моды за счет оставшейся интенсивности во 2-й. При этом, как показывают расчеты, в точке максимума второго каскада 2-я мода (накачка) практически исчезает, так что добавление последующих каскадов становится нецелесообразным. Однако для существенно меньших начальных интенсивностей WJ0 насыщение 1-ой (сигнальной) моды достигается за три каскада (или более), обеспечивая в конечном итоге высокие коэффициенты усиления. При этом энергетический интеграл 2 ■ W( + W2 = Const ограничивает максимальные значения выходной интенсивности: W™ax =0,5 W20 + W10.

Альтернативой многокаскадному усилению является непрерывное по длине, но слабое подавление 3-й моды. Например, близость ее к отсечке может описываться добавлением слабого затухания (-а • f3) в уравнение для df3/d? системы (2). При этом, как нетрудно показать, эволюция мод снова не зависит от начальных фаз (разумеется, если W3Q = 0). Вариантные расчеты при различных а в диапазоне от 0 до 0,2 позволили найти aopt — 0,1 (рис. 2). При этом следует отметить определенную ненадежность слабого подавления моды, что обусловлено сильным влиянием на а случайных факторов (например, температуры).

Для прикладных аспектов большое значение имеет зависимость коэффициента усиления от уровня входного сигнала при оптимальном выборе параметров усилителя. Соответствующие кривые изображены на рис. 3 для однокаскадной и двухкаскадной конфигурации (соответственно сплошная и пунктирная линии). Из них видно, что при небольших уровнях входного сигнала (W^q — от 0,01 до 0,15) схема работает вдали от насыщения, т. е. имеет место наиболее желательной режим линейного (по W₁₀) усиления (рис. 4).

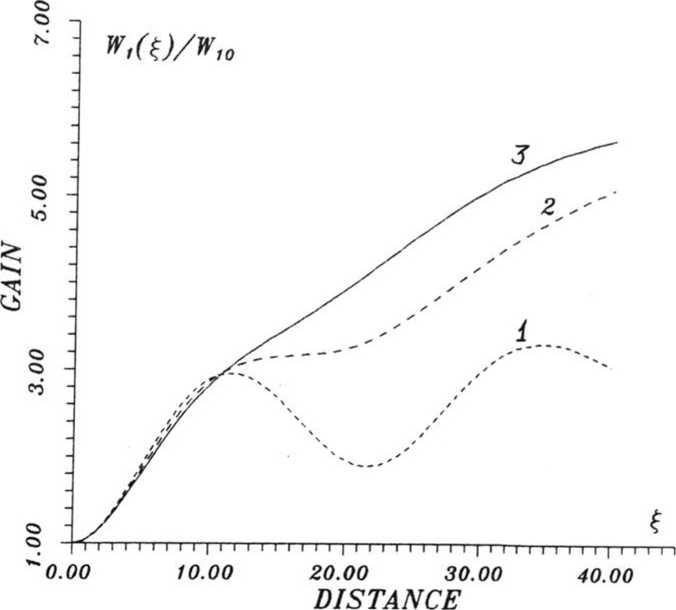
Рис. 2. Коэффициент усиления сигнальной моды для W1Q = 0,1, W2Q = 1, W3Q = 0 при непрерывном слабом подавлении третьей моды:

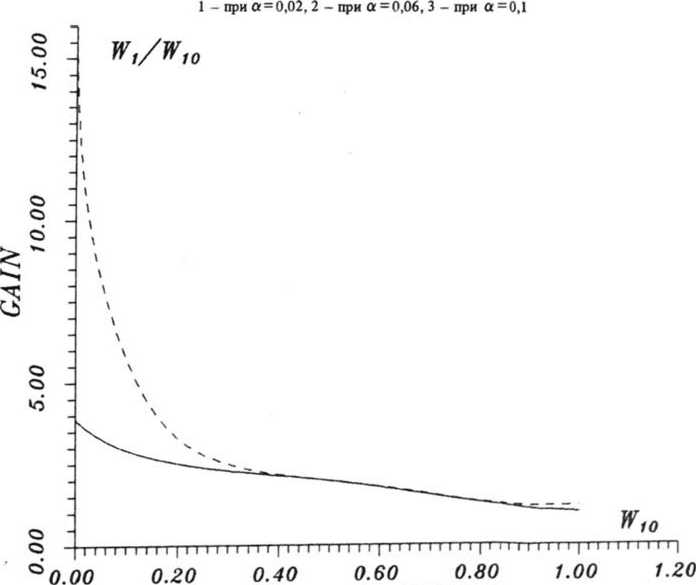
INPUT SIGNAL

Рис. 3. Зависимость коэффициента усиления сигнальной моды на выходе от уровня выходного сигнала для ^20 = *• W30 = 0, а = 0. Сплошная линия — 1-й каскад (выходное сечение {, = 11). Пунктирная кривая -двухкаскадное усиление: выходное сечение $2 * 25 (предполагается, что первый каскад закончился в т. ^ = 11, после чего на коротком отрезке подавлена и восстановлена 3-я мода)

gain

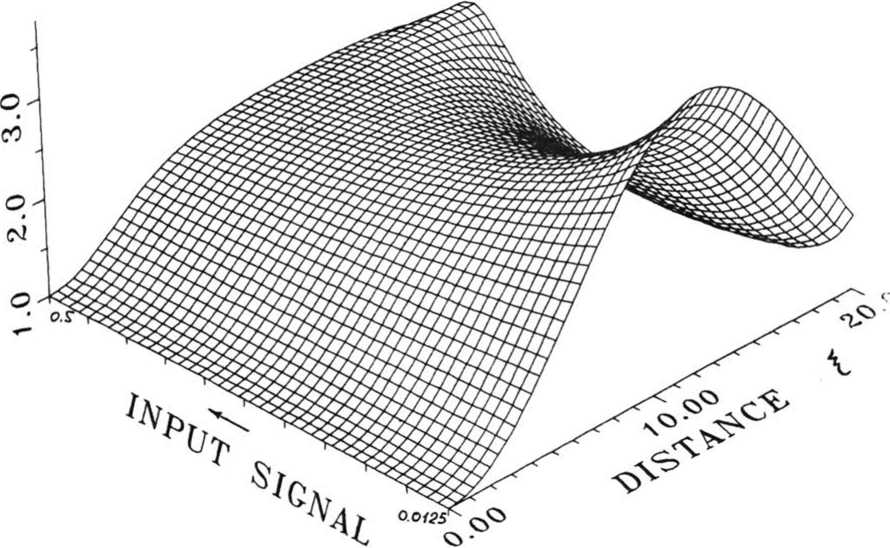
Рис. 4. Распределение интенсивности сигнала по длине световода £ при различных уровнях входного сигнала — от 0,0125 до 0,5