Трехуровневая упруговязкопластическая модель: анализ влияния величины энергии дефекта упаковки на отклик материалов при сложном нагружении
Автор: Грибов Д.С., Трусов П.В.
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
Разработка новых и совершенствование существующих режимов термомеханической обработки металлов и сплавов в современных условиях невозможны без создания соответствующих математических моделей, позволяющих с необходимой точностью определять характеристики материалов в проектируемых технологических процессах. «Сердцевиной», основной составляющей, определяющей качество таких моделей, являются конститутивные (определяющие) соотношения. В качестве таковых при решении прикладных задач механики деформируемого твердого тела широкое распространение получили макрофеноменологические теории неупругости, основанные на обработке результатов экспериментов на макрообразцах. С учетом необходимости описания свойства памяти, соотношения данного класса имеют сложную математическую структуру, требуют проведения дорогостоящих испытаний (вообще говоря - на сложное нагружение) для каждого конкретного материала, в силу чего не обладают универсальностью. В последние 15-20 лет все большую популярность приобретают конститутивные модели, основанные на введении внутренних переменных, многоуровневом подходе и физических теориях неупругости (пластичности, вязкопластичности). Модели этого класса ориентированы на описания эволюционирующей структуры (включая дефектные субструктуры), определяющей в конечном итоге физико-механические свойства материалов и эксплуатационные характеристики изделий из них. Поскольку физические механизмы и их носители идентичны для широких классов материалов, модели указанного класса обладают значительной универсальностью, в том числе они могут использоваться для прогнозирования поведения новых, еще не существующих материалов, изучения физических механизмов возникновения различных эффектов, наблюдаемых в макроэкспериментах. Одним из интересных эффектов является значительное увеличение сопротивления деформации в экспериментах на сложное (включая циклическое) нагружение (по сравнению с простым нагружением) образцов из различных металлов и сплавов, возникающее вследствие существенной эволюции микроструктуры. Анализ известных эмпирических данных позволил установить, что склонность к проявлению данного эффекта испытывают обычно металлы и сплавы, обладающие низкой энергией дефекта упаковки (ЭДУ). В работе приведен краткий анализ экспериментальных работ и математических моделей, описывающих отклик материала на сложное деформирование. Отмечается, что макрофеноменологические теории не позволяют описывать в явном виде эволюции микроструктуры и носителей механизмов деформирования и упрочнения, в силу чего не предоставляют возможности объяснить физические причины упомянутых эффектов. Цель исследования - разработка, изучение и реализация многоуровневой упруговязкопластической модели, позволяющей явным образом описывать эволюцию дефектов кристаллической решетки материалов с разной ЭДУ при разных термомеханических воздействиях, механизмы упрочнения на различных структурно-масштабных уровнях. В рамках построения конститутивной модели особое внимание уделено разработке подмодели, ориентированной на описание эволюции плотностей дислокаций и барьеров различной природы на системах скольжения. Эволюционные уравнения для плотностей дислокаций на системах скольжения позволяют анализировать зарождение дислокаций за счет активации источников Франка - Рида, аннигиляцию дислокаций разных знаков на одной системе скольжения, взаимодействия расщепленных дислокаций пересекающихся систем скольжения с образованием барьеров. Приведены соотношения для описания упрочнения, учитывающие текущую плотность дислокаций и барьеров. Рассмотрена общая структура модели и связи между параметрами подмоделей разных уровней. Разработан алгоритм и программа реализации модели, проанализирована эволюция плотностей дислокаций на системах скольжения, получены характеристики интенсивности упрочнения и образования барьеров на расщепленных дислокациях в зависимости от вида нагружения.
Сплавы, многоуровневая упруговязкопластическая модель, сложное нагружение, микроструктура, дислокации, барьеры на расщепленных дислокациях, законы упрочнения
Короткий адрес: https://sciup.org/146282026
IDR: 146282026 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.4.06
Текст научной статьи Трехуровневая упруговязкопластическая модель: анализ влияния величины энергии дефекта упаковки на отклик материалов при сложном нагружении
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2020PNRPU MECHANICS BULLETIN
Построение моделей, позволяющих описать изменение физических свойств металлов и сплавов при механических и термических воздействиях, является одной из наиболее важных и актуальных задач механики деформируемого твердого тела, физического материаловедения и прикладных дисциплин, ориентированных на описание процессов обработки материалов. Физикомеханические свойства моно- и поликристаллических металлов и сплавов зависят от типа кристаллической решетки, характера связей атомов, зеренной (субзеренной) и дефектной структур. Изготовление большинства используемых в практической деятельности металлических изделий осуществляется с использованием различных способов термомеханической обработки, часто -с применением методов интенсивной неупругой деформации. При термомеханических воздействиях на металлические материалы происходит существенное изменение их структуры и, как следствие, физических (механических, термических, электромагнитных и др.) свойств. Разработка технологических режимов обработ- ки металлов и сплавов методами пластической деформации в современных условиях немыслима без применения соответствующих математических моделей, поскольку используемые для этих целей в предшествующем веке эмпирические методы чрезвычайно ресурсоемки. В большинстве случаев в практике технологических организаций для установления рациональных режимов обработки применяются модели, основанные на макрофеноменологических теориях термоупругопластичности (в том числе в известных коммерческих пакетах). Модели данного класса позволяют определять напряженно-деформированное состояние на макроуровне, усилия и мощность, необходимые для реализации обработки, однако не дают возможности исследовать эволюционирующую в ходе процесса структуру материала, а следовательно, прогнозировать физикомеханические характеристики изделия. В связи с указанным обстоятельством в последние десятилетия все большую популярность приобретают многоуровневые (чаще всего двухуровневые) модели, основанные на введении внутренних переменных и физических теориях пластичности [Follansbee, Kocks, 1988; Anand, 2004; Franz et al., 2009; Horstemeyer, 2009; McDowell, 2010; Roters, 2011; Hu, Cocks, 2016; Трусов, Швейкин, 2019; и др.]. В двухуровневых (макро- и мезоуровень) моделях на низшем (мезо-) масштабном уровне описание ведется в терминах сдвигов (скоростей сдвигов) по системам скольжения (СС) кристаллитов, упрочнение на СС устанавливается феноменологическими законами. В последние 15–20 лет появились более «тонкие» трехуровневые модели [Arsenlis, Parks, 2002; Tinga et al., 2005; Fajoui et al., 2009; Groh et al., 2009; Beyerlein et al., 2011; Hamelin et al., 2011; Lim et al., 2011; Ardeljan et al., 2014, 2016; и др.], в которых на нижнем (микро-) уровне рассматриваются эволюция плотностей дислокаций на СС, скорости сдвигов определяются с использованием уравнения Орована, законы упрочнения формулируются в терминах взаимодействующих дислокаций.
Трехуровневые упругопластические модели позволяют не только описать поведение материалов при сложных воздействиях, но и объяснить физические причины возникновения интересных эффектов, давно обнаруженных экспериментально [Белл, 1984а, б; Аннин, Жигалкин, 1999; Зубчанинов, 2000], но не нашедших до настоящего времени адекватного физического обоснования. К числу таких эффектов относится обнаруженное во второй половине ХХ в. явление дополнительного упрочнения при сложном монотонном и циклическом нагружении. В предлагаемой статье рассматривается трехуровневая упруговязкопластическая модель, приведены модифицированные соотношения для описания эволюции плотностей дислокаций и упрочнения на системах скольжения. Особое внимание уделено учету влияния на кинетику дислокационных взаимодействий энергии дефекта упаковки (ЭДУ). Величина ЭДУ материала существенно влияет на эволюцию дефектной микроструктуры: для материалов с низ- кой ЭДУ при вовлечении в деформирование большого числа систем скольжения (что наблюдается при сложном деформировании) интенсифицируются процессы образования барьеров за счет взаимодействия расщепленных дислокаций, что приводит к существенному росту критических напряжений на СС.
1. Сложное нагружение: краткий обзор экспериментальных результатов и подходов к теоретическому исследованию
В реальных процессах обработки металлов и сплавов методами интенсивной пластической деформации (ИПД) реализуются, как правило, весьма сложные траектории деформирования различных частей обрабатываемых изделий. В связи с этим результаты экспериментов на сложное монотонное и непропорциональное циклическое деформирование металлов представляют большой интерес; при таких программах деформирования образуются субструктуры и свойства, которые невозможно получить при простом нагружении. В части работ, описывающих эксперименты на сложное деформирование, авторы отмечают связь величины ЭДУ исследуемых материалов и интенсивности упрочнения: для материалов с низкой ЭДУ характерно более активное упрочнение по сравнению с материалами с высокой ЭДУ при одинаковых программах деформирования.
В работах Беналляля и соавторов [Benallal, Marquis, 1987,1988; Benallal et al., 1989] приведены методика и результаты ряда экспериментов на простое (пропорциональное) и сложное (непропорциональное) циклическое деформирование в двухмерном пространстве деформаций – напряжений (осевые растяжение – сжатие и кручение тонкостенных трубчатых образцов), исследуемые материалы – нержавеющая сталь 316 и сплав алюминия 2024. Используемые траектории деформации приведены на рис. 1: а – растяжение; б – растяжение с одновременным кручением; в, г – пилообразные траектории, растяжение сменяется кручением, число зубцов варьировалось; д, е – последовательное растяжение и кручение с промежуточным реверсивным деформированием, между лучами углы в 90° и 45°; ж – последовательное растяжение с кручением по замкнутой траектории в форме квадрата; з – одновременное растяжение и кручение по замкнутой траектории в форме эллипса. Образцы были отожжены перед деформированием, микроструктура материалов не анализировалась. Было отмечено удовлетворительное соответствие экспериментальных данных теоретическими результатам, полученным с использованием теорем о приспособляемости Мелана и Койтера [Койтер, 1961]. Приведено описание явления дополнительного циклического упрочнения, явления разупрочнения при смене программы нагружения со сложного на простое и эффекта перекрестного упрочнения. В работе отмечено известное из ранее проведенных эмпирических исследований явление – переход зависимостей напряжений от деформаций на ста- ционарные траектории при фиксированных амплитудах пластических деформаций после 20–40 циклов (приспособляемость материала к программе нагружения). Также в работе описаны результаты экспериментов на циклическое простое и сложное нагружение, приведены значения пределов текучести после деформирования по различным программам нагружения.
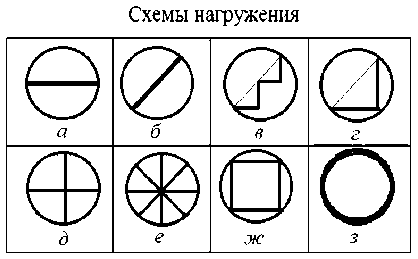
Рис. 1. Схематическое изображение программ деформирования из экспериментов на циклическое деформирование [Benallal, Marquis, 1987]
Fig. 1. Schematic representation of deformation schemes on cyclic deformation experiments [Benallal, Marquis, 1987]
Дополнительным циклическим упрочнением (ДЦУ) называется повышение предела текучести материала после сложного (непропорционального) циклического деформирования по сравнению с пределом текучести, получаемым после опытов на простое (лучевое, пропорциональное) циклическое нагружение с теми же амплитудными значениями интенсивностей деформации. Процессы сложного циклического деформирования в общем случае – процессы с траекторией в форме замкнутой кривой в пространстве деформаций (мера сложности нагружения не обсуждается). В цитируемых работах при испытаниях тонкостенных трубчатых образцов для анализа явления ДЦУ использовалось две моды деформирования: знакопеременное кручение (со сдвиговыми деформациями γ) и растяжение – сжатие (с продольной деформацией ε), при постоянных для каждого испытания амплитудах γ m и ε m , с одинаковой частотой ω, но с рассогласованием по фазе на произвольный угол f :
Y = Y m sinH + f ), ε = ε m sin(ωt), p =
γ m
/ л/Зе
m
Величина дополнительного упрочнения зависит от параметров процесса ρ и f и может достигать десятков процентов (рис. 2).
В цитируемых работах отмечено наблюдаемое в экспериментах последовательное разупрочнение – снижение предела пластичности при смене программы циклического нагружения с непропорциональной на пропорциональную, и эффект перекрестного упрочнения – увеличение предела пластичности при смене типа сложного циклического нагружения. Показано также повышение предела пластичности на 15 % при смене типа нагружения с растяжения на кручение для стали, т.е. ДЦУ возникает, хотя и в меньшей степени, при по- следовательных, отличающихся друг от друга простых
циклических нагружениях.
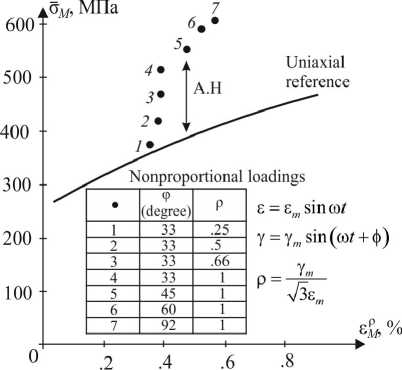
Рис. 2. Зависимость амплитудных значений интенсивности напряжений от амплитуды пластических деформаций для семи экспериментов (точки 1–7, номера соответствуют программам, приведенным в таблице, f (φ) – угол сдвига фазы между модами деформации) в сравнении с одноосным нагружением (сплошная кривая) [Benallal, Marquis, 1987]
Fig. 2. Dependence of the amplitude values of the stress intensity and the plastic deformations for seven experiments (points 1-7, the numbers correspond to the programs, f (φ) is the phase lag between the deformation modes) in comparison with uniaxial loading (solid curve) [Benallal, Marquis, 1987]
В работах [Feltner, Laird, 1967a, b] представлены методика и результаты экспериментов на циклическое деформирование образцов из чистой и легированной меди при различных температурах. Рассматривались закономерности выхода на установившуюся петлю гистерезиса при циклическом пропорциональном нагружении. В случае предварительного пластического деформирования отмечено смещение петли гистерезиса в направлении предварительного деформирования, для материалов с низкой энергией дефекта упаковки данный эффект проявляется более интенсивно. Приведены также данные анализа микроструктуры образцов после циклического деформирования. Отмечено образование дислокационных стенок для чистой меди, а также образование полос скольжения для сплава медь – алюминий 7,5 %. На основании исследования микроструктуры было сделано предположение о наличии аккомодационного механизма накопления и сброса накопленной энергии путем увеличения и сжатия дислокационных петель при циклическом нагружении.
Работа [Lamba, Sidebottom, 1978] посвящена рассмотрению результатов экспериментов на медных (с относительно низкой ЭДУ) образцах. В работе отмечен выход на установившийся цикл кривой напряжения – деформация при циклическом нагружении образцов из чистой меди. Образцы подвергались предварительному деформированию по циклическим простым и сложным траекториям, наблюдалось явление ДЦУ. Особое внимание уделяется восстановлению установившегося режима при простом циклическом нагружении, следующем за этапом сложного циклического нагружения, что указывает на затухающую память материала.
В работе [Laird et al., 1986] представлены результаты экспериментов по деформированию образцов из меди и сплава меди с алюминием при циклическом нагружении. Основной целью экспериментов было исследование накопления дефектов, приводящего к образованию ячеистой структуры в кристаллитах и дальнейшему разрушению. Приведены и описаны этапы формирования и эволюции микроструктуры в ходе циклического деформирования, в том числе начальный период, при котором происходило образование барьеров на расщепленных дислокациях и накопление поджатых на барьерах дислокаций.
В работе [Trampzinsky, 1988] рассмотрены результаты экспериментов, полученные на образцах из сталей 18Г2А и 2CrMoV57. Кинематические программы включали простой сдвиг, кручение, циклический сдвиг, циклическое кручение и сжатие. Образцы нагружали монотонно и циклически с постоянной интенсивностью скорости деформаций при контролируемой амплитуде деформаций и комнатной температуре. В работе отмечены следующие основные результаты: при простом циклическом нагружении выход на стационар при циклическом нагружении устанавливается при первом цикле, а затем он незначительно изменяется, не наблюдается расширения петли гистерезиса. Значения максимальных (по модулю) напряжений петли гистерезиса зависят от амплитуды пластической деформации. В экспериментах отмечено явление ДЦУ (при деформировании по круговым траекториям в пространстве деформаций).
В исследовании [Doquet, Pineau, 1990] рассматривалось пропорциональное и непропрорциональное циклическое деформирование стальных образцов. Проведен анализ напряженного состояния и исследована структура образцов. Анализ поверхности показал, что непропорциональное нагружение создает более однородное скольжение в разных зернах, чем пропорциональное; отмечено также, что непропорциональное нагружение увеличивает количество активных систем скольжения. Результаты удовлетворительно согласуются с данными работ группы Беналляля.
В работе [Xia, Ellyin, 1991] анализируются результаты испытания на двухосное деформирование тонкостенных круглых цилиндрических образцов из низколегированной углеродистой стали. Рассматривались непропорциональные циклические нагружения, растяжение и кручение изменялись по гармоническому закону от времени. Изучалось влияние амплитуды деформации и фазового угла (меры непропорциональности пути деформации). При анализе результатов эксперимента отмечено проявление анизотропии и явление ДЦУ, возникающее в результате непропорционального циклического деформации. Представлена конститутивная модель, описывающая с приемлемой точностью поведение материала при сложных историях нагружения, включая циклическую деформацию.
В работе [Doquet, 1993] обсуждаются результаты испытаний образцов из материала с низкой энергией упаковки – сплава кобальт – 33 % никель. ДЦУ, возникающее в этом материале при непропорциональном циклическом нагружении трубчатых образцов на растяжение – кручение, очень существенно и достигает десятков процентов. Основное внимание в работе уделено физическому объяснению образования в процессе деформирования двойников. Образование двойников требует повышенных действующих напряжений, что достигается благодаря предварительному этапу формирования микроструктуры. По мнению авторов, после образования барьеров Ломера – Коттрелла происходит блокирование скольжения по многим системам скольжения, что приводит к существенному повышению критических напряжений. При проведении испытаний на растяжение и кручение при самых малых диапазонах деформации отмечалось ускорение циклического упрочнения после 6–10 циклов, когда уровни напряжений достигали 180–200 МПа (для материала без упрочнения предел текучести равен 100 МПа), что связывается с ранним образованием двойников.
Одна из первых попыток теоретически описать процессы циклического деформирования была предпринята еще во второй половине 60-х гг. P.J. Armstrong и C.O. Frederick [Armstrong, Frederick, 1966; Frederick, Armstrong, 2007], подход был основан на принципе запаздывания А.А. Илюшина [Илюшин, 1963]. Макрофе-номенологические модели в большинстве случаев основаны на теории пластического течения и модификации законов упрочнения для описания изменения поверхности текучести в ходе пластического деформирования, отличаясь главным образом способом учета памяти материала в ходе пластического деформирования [Tanaka et al.,1985; Chaboche, 1989; McDowell, 1992; Haupt, Kamlah, 1995; Бондарь и др., 2017; Бондарь, Абашев, 2019]. Изменение поверхности текучести связывается со сложностью и интенсивностью нагружения, для описания вводятся функционалы с идентифицируемыми в ходе натурных экспериментов параметрами. Учитывается затухающая память процесса. В большинстве случаев результаты применения данных моделей дают близкие к экспериментальным данным значения, но имеют и недостатки, к которым в первую очередь относятся ограниченность диапазона и размерности пространства (напряжений – деформаций) при реализации необходимых для построения рассматриваемых теорий пластичности экспериментов. К недостаткам относятся также неуниверсальность определяющих соотношений, необходимость их «настраивания» для разных классов материалов и процессов деформирования, потребность в эмпирической идентификации и верификации для конкретных марок сплавов и историй изменения НДС без возможности применения данной информации для других материалов.
2. Концептуальная и математическая постановка
В настоящей работе была использована модель, основанная на введении внутренних переменных [Rice, 1971; Жермен, 1983; Germain et al., 1983; Можен, 1992; Maugin, 2015] и физических теориях пластичности (ФТП) [Taylor, 1938; Lin, 1957; Roters et al., 2010; Roters, 2011; Трусов, Швейкин, 2011, 2019]. Согласно подходу, основанному на введении внутренних переменных, реакция материала в каждый момент времени полностью определяется значениями тензорзначных термомеханических характеристик материала и конечного набора внутренних переменных, параметров физико-механических воздействий и их производных по времени требуемого порядка в исследуемый момент времени [Трусов и др., 2009; Трусов, Швейкин, 2011].
На каждом из входящих в рассмотрение структурно-масштабных уровней внутренние переменные делятся на два класса: явные и неявные. Явные внутренние переменные входят в определяющие соотношения, неявные служат для описания эволюции структуры материала и процессов на более низких (по отношению к описываемому) масштабных уровнях. Анализ существующих моделей материала и физических механизмов неупругого деформирования широкого класса конструкционных материалов позволяет предложить структуру конститутивной модели, включающую определяющие соотношения, эволюционные и замыкающие уравнения. Преимущество данного подхода заключается в базировании на фундаментальных физических законах, более ясной физической интерпретации внутренних переменных, возможности обработки получаемых данных с использованием различных методов и сравнения получаемых с использованием модели структур со структурой материала, наблюдаемой при натурных экспериментах [Трусов, Швейкин, 2011, 2019].
В предлагаемой работе в рассмотрение для описания поведения поликристаллического образца вводятся следующие структурно-масштабные уровни: макроуровень, мезоуровень-1 и мезоуровень-2. Ключевым механизмом неупругого деформирования в данной работе полагается движение краевых дислокаций. На мезоуровне-2 его описание осуществляется с использованием введения плотностей дислокаций на системах скольжения (СС) и скоростей их движения; на мезоуровне-1 неупругое деформирование рассматривается в терминах скоростей сдвигов по кристаллографическим СС. Для связи подмоделей различных уровней в структуру определяющих соотношений на каждом из масштабных уровней вводятся явные внутренние пере- менные, определяемые из замыкающих уравнений, описывающих процессы деформирования на более глубоких масштабных уровнях по отношению к рассматриваемому [Трусов, Швейкин, 2011]. На макроуровне описывается поведение представительного макрообъема материала в терминах тензора напряжения, упругих и пластических составляющих тензора деформации. Элемент макроуровня (макро-точка, представительный макрообъем) является иерархически старшим по отношению к некоторой совокупности элементов мезоуровня-1. Иерархическое строение модели (рис. 3) позволяет рассчитывать напряженно-деформированное состояние во всех элементах нижележащего уровня, в дальнейшем производя осреднение по объему. В качестве воздействия на мезоуровень-1 с макроуровня передаются кинематические параметры (принимается гипотеза Фойгта о равенстве градиентов скоростей перемещений двух уровней). Макроточка может использоваться для решения краевой задачи; неупругая составляющая тензора деформации скорости макроуровня определяется осреднением неупругих составляющих скоростей деформаций элементов мезоуровня-1. При описании деформирования кристаллита используется модель мезоуровня-1 и подмодель мезоуровня-2. На мезоуровне-1 описывается механическое состояние кристаллита. Определяемые на мезоуровне-1 касательные напряжения на системах скольжения передаются в качестве воздействия на мезоуровень-2, где рассматривается эволюция плотностей дефектов, описывается упрочнение, определяются скорости движения дислокаций, а по ним с использованием уравнения Орована – скорости сдвигов по СС. С мезоуровня-2 на мезоуровень-1 передаются скорости сдвигов по системам скольжения. Для упрощения изложения принимается предположение об изотермич-ности процесса деформирования.
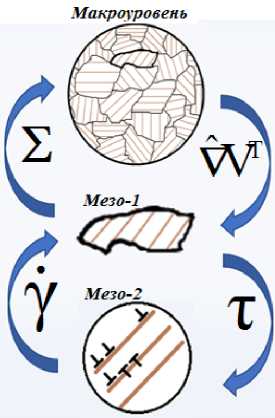
Рис. 3. Схематическое изображение структуры модели, прямых и обратных связей между уровнями
Fig. 3. Schematic representation of the structure and relations between of the model levels
В модели мезоуровня-2 используется разделение плотностей дислокаций по системам скольжения на положительные и отрицательные (по заранее условленному правилу, в зависимости от направления экстраплоскости). Переменными мезоуровня-2 являются: плотности (положительных и отрицательных) дислокаций, плотности источников дислокаций и барьеров на СС. К внутренним переменным мезоуровня-1 относятся скорости сдвигов по системам скольжения и критические напряжения, которые определяются дислокационной субструктурой. На мезоуровне-2 описывается эволюция плотностей дислокаций по СС и образование барьеров на расщепленных дислокациях. В ГЦК-мате-риалах с низкой энергией дефекта упаковки (ЭДУ) дислокации имеют склонность к расщеплению на две частичные и дефект упаковки [Орлов, 1983]. В случае реакции между двумя расщепленными дислокациями, движущимися по сопряженным СС, может образоваться барьер, состоящий из двух частичных и головной (сидячей) дислокации, запирающий скольжение по двум СС (важно отметить, что запираются только две СС, не все множества параллельных кристаллографических плоскостей с одним направлением). Величина энергии дефекта упаковки (ЭДУ) влияет на склонность дислокаций к расщеплению и на среднюю ширину расщепления; ЭДУ сплавов обычно ниже для легированных материалов и может уменьшаться в разы при увеличении доли примеси на 5-10 %.
Основным в предлагаемой работе является детальное, физически обоснованное описание дислокационного скольжения, взаимодействия дислокаций друг с другом, а также взаимодействие расщепленных дислокаций с образованием барьеров Ломера - Коттрелла и Хирта [Фридель, 1967; Хирт, Лоте, 1972]. Барьеры вносят существенный вклад в увеличение критических напряжений, затрудняя скольжение дислокаций по соответствующим СС.
На макроуровне описывается поведение представительного объема материала, описывается механический отклик представительного макрообъема материала; каждый элемент макроуровня соотносится с точкой интегрирования при решении краевых задач с использованием метода конечных элементов. С использованием гипотезы Фойгта с макроуровня на мезоуровень-1 передается градиент скорости перемещений V :
по обозн „ z = Z = V VT, где V — оператор градиента (Гамильтона), определенный в актуальной конфигурации, «Т» - знак транспонирования.
На мезоуровне-1 определяются пластическая составляющая меры скорости деформации zin и компоненты тензора напряжений Коши ст; с мезоуровня-1 на мезоуровень-2 передаются действующие касательные напряжения т(к). Скорости сдвигов у(к) определяются на мезоуровне-2 по скоростям движения дислокаций и ис пользуются для вычисления неупругой составляющей меры скорости деформации на мезоуровне-1. Подмодель мезоуровня-1 включает следующую систему уравнений:
СТ + ст • to — го • ст = п :( z - го - z in ), z = z е + z n ,
T
-
< to = o • o ,
z n = £ Y k ) b ( k ) n ( k ) , к = 1
т( k) = b(k )n(k): ст, где СТ - тензор напряжений Коши; п - 4-валентный тензор упругих характеристик (с постоянными компонентами в «решеточном» базисе); ze - упругая составляющая меры скорости деформации; zin - мера пластических деформаций; о - ориентационный тензор; го - спин решетки; b - единичный вектор в направлении вектора Бюргерса краевой дислокации; n - нормаль к плоскости скольжения дислокации; у - скорость сдвига по СС, индекс к обозначает номер системы скольжения (СС). Описание эволюции дислокационной субструктуры производится на мезоуровне-2. К явным внутренним переменным (ВП) мезоуровня-1 относятся п, ст, го, zin.
Эволюционные уравнения для плотностей дислокаций на СС включают соотношения для описания зарождения дислокаций за счет работы источников Франка-Рида, аннигиляции дислокаций разных знаков на одной СС, изменения плотности барьеров на СС. Значение критических напряжений на СС определяются текущей плотностью дефектов на всех системах. К явным внутренним переменным на мезоуровне-2 относятся средние скорости дислокаций V ± к ) , зависящие от касательных напряжений т ( к ) , температуры 0, плотности положительных и отрицательных дислокаций p + k ) , р — к ) и плотности барьеров p k на СС. Полная скорость изменения критических напряжений сдвига т *к ) полагается равной сумме составляющей за счет изменения плотностей дислокаций по СС т Ск ) дисл и вклада от изменения плотностей барьеров т Ск ) бар, образуемых расщепленными дислокациями. Скорости сдвигов определяются с использованием уравнения Орована в скоростной форме. Подмодель мезоуровня-2 представляется следующей системой соотношений (часть из которых записана в общем виде, детализированном ниже):
V к ) = ± f 1 ( т ( к ) , т Ск ) , 0 ) sign ( т ( к ) ), Y ( k ) = ( p + k ; k ) -p — k ) ) |Ь|( к ) , p ( k ) = f ^т k ) , т ск ) , о , p ( k ) , p ( kr ), Р bar (“’ = f з ( Т ( к ) , Т Ск ) , 0 , р ( к ) , С ), Т Ск 0) Т е ,
т ( к ) -т ( к ) ,т ( к )
-
т c т c _ дисл т c _ бар .
Для описания дислокационных реакций важнейшую роль играют средние скорости дислокаций ( V +′( k ) , V -′( k ) ), при этом скорости движения дислокаций противоположных знаков на одной и той же кристаллографической плоскости могут отличаться знаком и величиной.
Как отмечено выше, для определения скоростей сдвигов по СС на мезоуровне-1 используется уравнение Орована в скоростях, включающее плотности положительных и отрицательных дислокаций, средние скорости скольжения дислокаций V -′( k ) , V +′( k ) (определенные в лабораторной системе координат (ЛСК)) и модуль вектора Бюргерса дислокаций:
Y ( k ) = ( p + k ) v + k ) -p - ) v - k ) ) |b| ( k )
Средние скорости движения дислокаций выражаются следующими соотношениями [Kocks, 1987; Balasubramian, Anand, 2002; Ma et al., 2006]:
V + k ) = lkv exp( -A G * / k B 6 ) H ( t ( k ) - т ) ) sign( T ( k ) ),
• (4)
Vхk) =-lkvexp(-AG* /kB6) H(|t(k)|-Tck)) sign(T(k)), где ΔG*k – энергия активации движения дислокаций (зависящая от свойств решетки и касательного напряжения на СС); kB – константа Больцмана; θ – температура; Н – функция Хэвисайда; lk – средняя длина свободного пробега дислокации k-й СС; v – дебаевская частота.
Знак перед выражением для определении средних скоростей сдвига зависит от знака дислокаций, для которых они определяются: для положительных знак по умолчанию – плюс, для отрицательных – минус.
Работа источников. При пластическом деформировании, как правило, имеет место увеличение плотности дислокаций на СС. В качестве внутризеренных источников дислокаций выделяются источники Франка– Рида, генерирующие замкнутые расширяющиеся петли дислокаций. Из экспериментов известно, что источник может генерировать ограниченное число петель. В работе для описания генерации дислокаций вводятся плотности источников Франка – Рида ρ( skrc ) (размерность м–3), изменение которых описывается следующими соотношениями:
( k ) ρ 0 src = ρ 0 src ,
p (Г) = 11 l p 1 p j [ Vv exp( -A G * / * b 6 ) H (| T ( j )| - т > ) ], (5)
где ρ b kj ar – плотность барьеров на пересечении k и j СС (препятствующая движению дислокаций на обеих этих СС). Вклад в увеличение плотностей дислокаций пропорционален текущей плотности петель и отличен от нуля только при превышении действующих касательных напряжений критических напряжений активации источников τ src :
p ( k ) nuc
τ ( k )
( k )
ср src τ src
-
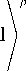
A ц b [. L D| τ= ln + B , src
2 n L l Г о )
где r ср – средняя длина петли; v – дебаевская частота; A, B, P – безразмерные параметры материала; μ – модуль сдвига; L – расстояние между препятствиями в источнике; r 0 – минимальная ширина закрепленного участка; b – величина вектора Бюргерса.
Аннигиляция дислокаций происходит в результате реакции дислокаций одной СС с разными знаками. Данная реакция возможна в случае, если две дислокации противоположных знаков оказались на небольшом удалении друг от друга. Аннигиляция дислокаций наиболее часто наблюдается в экспериментах на реверсивное нагружение. Дислокации разных знаков в одной системе скольжения притягиваются, при нахождении дислокаций на параллельных системах скольжения они могут переползать в направлении друг к другу, аннигилируя при сближении на расстояние аннигиляции h ann . Количество прореагировавших дислокаций в единицу времени пропорционально заметаемому объему и плотности дислокаций на системах скольжения. Для описания аннигиляции в работе предлагается использовать следующее соотношение:
p ( k ) ann =— h ann P +k ) P - k ) V k ) — V - k )| .
Эволюция барьеров описывается с использованием построенной матрицы плотностей барьеров R b k a l r , в которой единичные значения на пересечении строки k и столбца l означают СС, в которых залегают расщепленные дислокации, реагирующие при пересечении с образованием барьеров; остальные компоненты матрицы R b k a l r – нулевые. Скорость изменения плотности барьеров зависит от плотности дислокаций на реагирующих системах, действующих касательных напряжений и температуры:
PL = axd RkL- plpk[lkv exp(—AG*k / *b6)], bb2G (8)
x d == ,
8πεДУ 8πγДУ где α – безразмерный параметр; xd – средняя ширина расщепления дислокации; εДУ – безразмерная величина ЭДУ (εДУ =γДУ Gb ) [Штремель, 1999]; γДУ – энергия дефекта упаковки. Матрица учета плотностей барьеров на СС содержит все 24 барьера на расщепленных дислокациях. Компоненты матрицы pkar описывают скорости изменения плотностей барьеров, образованных на пересечении дислокаций, принадлежащем k-м и l-м CC;
таким образом, описываются плотности барьеров, образуемых в ходе реакций, описываемых построенной матрицей R b k a l r [Trusov et al., 2016]. Компоненты матрицы R b k a l r равны единице, если дислокации СС с индексами k и l могу образовать устойчивый барьер Ломера – Коттрелла или Хирта [Фридель, 1967; Хирт, Лоте, 1972].
При описании закона упрочнения принимается гипотеза о возможности аддитивного разделения критических напряжений СС на вклады от сопротивления решетки (неизменная величина), от полей напряжений дислокаций и образованных на расщепленных дислокациях барьеров. Для определения составляющей, описывающей влияние накопленных дефектов, было оценено влияние дислокаций различных СС друг на друга. Для оценки действия полей напряжений одной дислокации на другую использованы известные решения [Фридель, 1967; Хирт, Лоте, 1972] для одиночной дислокации в изотропной упругой среде. На основе данного решения была построена матрица Mki , позволяющая оценить напряжения взаимодействия дислокаций k -й и i -й СС, которые заносятся на пересечении k -й строки и i -го столбца матрицы Mki . Введение барьера на расщепленной дислокации как комплекса из двух частичных и сидячей дислокации позволило оценить влияние барьера на упрочнение k -й СС за счет барьера на i -й СС, для описания этого влияния используется матрица Вki , построенная подобно матрице Mki. Компоненты матриц были нормированы на начальные критические напряжения соответствующих систем скольжения (напряжения Пайерлса) τ ( ck 0) =τ ( сk _)реш и являются безразмерными величинами. С использованием введенных матриц эволюционные соотношения для изменения критического напряжения сдвига и его составляющих можно записать в следующем виде:
-
( k ) ( k )
τ c 0 =τ с _реш ,
т( k) = т( k) + Т k) τc τc_ дисл τc_ бар , n ki tkU = a b Т» ^ M^ P-, (9)
-
i = 1 2 ρ i
nki
-
( k ) ( k ) B ki
τc бар =βτc0 ∑ ρbar ,
3. Анализ результатов
_бар 0 i=1 2 ρki ρbar где α, β – безразмерные параметры материала.
Приведенная выше модель была реализована на языке С++ в процедурной парадигме для пошагового (в физическом времени) решения совокупности уравнений описанной модели. Для решения системы обыкновенных дифференциальных уравнений использовалась явная схема Эйлера. Данная подмодель представляет собой отдельный блок, предназначенный для включения в конечно-элементный пакет, разработанный на кафедре ММСП ПНИПУ и реализованный в объектноориентированной парадигме для описания деформирования конструкций.
Основные переменные мезоуровня-2
Basic Mesoscale-2 variables
|
Обозначение переменной |
Значение |
Размерность |
|
τ ( k ) , τ ( ck ) |
Касательные на СС напряжения, критические напряжения |
МПа |
|
ρ ( + k ) ρ ( - k ) |
Плотности дислокаций на СС |
м –2 |
|
ρ (0 ks ) rc |
Плотности источников дислокаций |
м –3 |
|
ρ ( bkar ) |
Плотности барьеров на расщепленных дислокациях |
м –2 |
|
b ( k ) |
Длина вектора Бюргерса |
м |
|
V - '( k ) |
Средние скорости скольжения дислокаций |
мс |
На данном этапе работы с целью качественной проверки разработанной подмодели (на способность описывать образование барьеров дислокационной природы, связи интенсивности формирования барьеров с величиной ЭДУ и упрочнение, обусловленное возникновением барьеров дислокационной природы) нагружения ограничены монотонными, по сложным траекториям деформации в двумерном пространстве. Приведены результаты применения подмодели для описания эволюции плотности дефектов в кристаллите (рассмотрение на уровнях мезо-1 и мезо-2) и поликристаллического агрегата из 64 элементов (макроуровень, мезо-1 и мезо-2). При численной реализации использовался временной шаг 0,001 с–1. Моделировалось упругопластическое деформирование чистой меди и латуни (Cu-20%Zn). Воздействие определено кинематически, заданы компоненты градиента скорости перемещений в базисе лабораторной системы координат (ЛСК): для простого сдвига ( z12 = z21 = 1 ⋅ 10 - 4c –1 ) и растяжения (z11 = 1 ⋅ 10 - 4c –1 , z22 = z33 = 5 ⋅ 10 - 5c –1 ). При анализе деформирования монокристалла в отсчетной конфигурации кристаллографическая система координат полагается совпадающей с лабораторной.
Был проведен ряд экспериментов на последовательное растяжение и сдвиг монокристаллов меди (ЭДУ 75 МДж м-2) и латуни (ЭДУ 20 МДж м-2), результаты которых представлены на рис. 4, 5. Смена направления деформирования происходила по достижении накопленной деформации, кратной 0,3 %. Приведены результаты расчета изменения плотностей дислокаций на СС (рис. 6). При смене типа деформирования отмечается как смена активных СС, так и следующее из этого различие характера эволюции плотностей дислокаций по СС. Две СС были задействованы все время, четыре системы не были активированы в ходе всего нагружения. В численных экспериментах по исследованию деформирования монокристаллов латуни был отмечен более быстрый рост числа барьеров на расщепленных дисло- кациях (рис. 7) и, как следствие, критических напряжений на всех СС латуни, что связано с более низкой ЭДУ по сравнению с медью. При одинаковой интенсивности накопленных деформаций в латуни интенсивность напряжений достигла 67 МПа, в меди – 39 МПа.
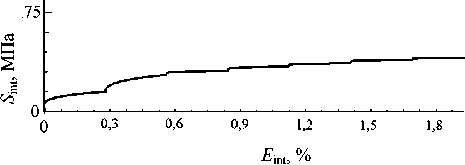
Рис. 4. Зависимость интенсивности напряжений от интенсивности накопленной пластической деформации при последовательных чередующихся этапах растяжения и сдвига (медь, ЭДУ 75 мДж м-2, монокристалл, ориентация кристаллографической системы координат совпадает с лабораторной)
Fig. 4. Dependence of the effective stress of the accumulated effective plastic strain at alternating stages of tension and shear (copper, SFE 75 MJ m-2, single crystal, the orientation of the crystallographic and laboratory coordinate systems are equal)
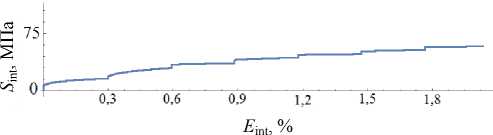
Рис. 5. Зависимость интенсивности напряжений от интенсивности накопленной пластической деформации при последовательном растяжении и сдвиге (латунь Cu–20%Zn, ЭДУ 20 мДж м-2, монокристалл, ориентация кристаллографической системы координат совпадает с лабораторной)
Fig. 5. Dependence of the effective stress on the accumulated effective plastic strain at alternating stages of tension and shear (brass Cu–20%Zn, SFE 20 MJ m-2, single crystal, the orientation of the crystallographic and laboratory coordinate systems are equal)
В экспериментах на последовательное растяжение и сдвиг ПО поликристаллического образца из меди, состоящего из 343 случайно ориентированных (по равномерному закону) кристаллитов, наблюдается увеличение модуля упрочнения при смене типа нагружения. На рис. 8 приведена зависимость интенсивности напряжений S int от интенсивности накопленных деформаций E int . Из полученных результатов следует отметить существенный рост критических напряжений по неактивным СС. Данный факт объясняется значительным увеличением плотностей дислокаций по активным СС (рис. 9), что, в свою очередь, повышает критические напряжения по всем остальным СС, и при смене программы деформирования ранее неактивные СС включаются в скольжение при более высоких значениях касательных напряжений.
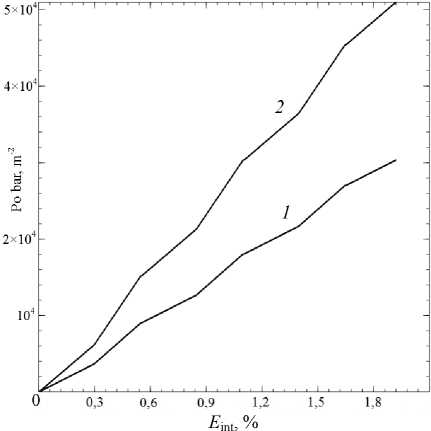
Рис. 7. Зависимость средней плотности барьеров по СС от интенсивности накопленных деформаций при последовательном растяжении и сдвиге. График ( 1 ) – монокристаллическая медь, график ( 2 ) – монокристаллическая латунь Cu–20%Zn
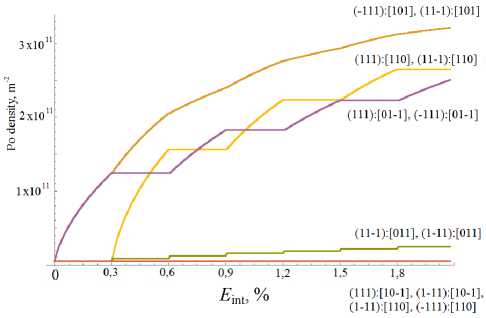
Рис. 6. Зависимость плотности дислокаций ρ по СС от интенсивности накопленных деформаций при последовательном растяжении и сдвиге (медь, ЭДУ 75 МДж м-2)
Fig. 7. Dependence of the average density of barriers on the accumulated effective strain during successive stretching and shear strain. Graph ( 1 ) – copper, graph ( 2 ) – brass Cu–20% Zn
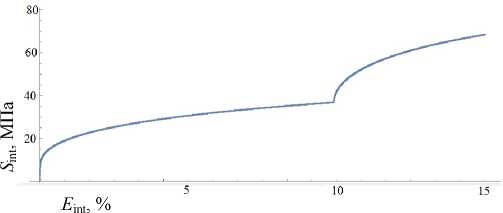
Рис. 8. Зависимость интенсивности напряжений от интенсивности накопленной пластической деформации при последовательном растяжении до 10 % и сдвиге на 7 % (медь, представительный макрообъем поликристалла, 343 кристаллита)
Fig. 6. Dependence of the dislocations density at the SS on the accumulated effective strain during successive tension and shear (copper, single crystal, SFE 75 MJ m-2)
Fig. 8. Dependence of effective stress on the accumulated plastic effective strain at successive tension up to 10% and shear by 7 % (representative macrovolume of a polycrystal, 343 crystallites, copper)
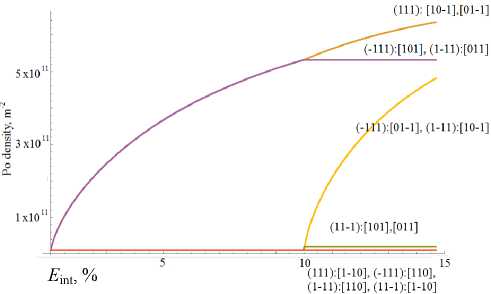
Рис. 9 Зависимость плотности дислокаций ρ по СС от интенсивности накопленных деформаций при растяжении до 10 % и последующем сдвиге на 7 % (приведены плотности дислокаций в случайно выбранном кристаллите с ориентировкой кристаллографической системы координат по отношению к ЛСК в углах Эйлера: а = 31°, в = 11°, у= 19°)
Fig. 9. Dependence of the dislocation density ρ at SS on the accumulated effective strain under tension up to 10 % and subsequent shear strain by 7 % (the dislocation densities in a randomly selected crystallite, with the orientation of the crystallographic coordinate system with respect to the laboratory coordinates system with the Euler angles: а = 31 ° , в = 11 ° , у = 19 ° )
Заключение
Представлено краткое описание экспериментальных данных на сложное (включая циклическое) нагружение. Приведен краткий обзор существующих моделей для описания деформирования материалов при непропор- циональном циклическом деформировании. Описаны основные механизмы эволюции микроструктуры. Представлена структура и основные соотношения многоуровневой модели для описания пластического деформирования материалов с разной ЭДУ, базирующейся на физической теории упруговязкопластичности. Предложена модификация подмодели мезоуровня, включающая описание эволюции плотностей краевых дислокаций и барьеров дислокационной природы, влияющих на критические напряжения скольжения.
Разработан алгоритм и программа реализации подмодели. Проведены предварительные численные эксперименты, качественно подтверждающие способность разработанной подмодели описывать формирование барьеров дислокационной природы и влияние на интенсивность образования последних величины энергии дефекта упаковки.
Работа выполнена при финансовой поддержке Минобрнауки РФ (базовая часть государственного задания ПНИПУ, проект № FSNM – 2020-0027).
Acknowledgment
This work was carried out with financial support from the Ministry of Education and Science of the Russian Federation (the basic part of the state assignment PNRPU, project No. FSNM-2020-0027).
Список литературы Трехуровневая упруговязкопластическая модель: анализ влияния величины энергии дефекта упаковки на отклик материалов при сложном нагружении
- Аннин Б. Д., Жигалкин В.М. Поведение материалов в условиях сложного нагружения. - Новосибирск: Изд-во СО РАН, 1999. - 342 с.
- Белл Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. Ч. 1. Малые деформации. - М.: Наука. Гл. ред. физ.-мат. лит., 1984а. - 600 с.
- Белл Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. Ч. 2. Конечные деформации. - М.: Наука. Гл. ред. физ.-мат. лит., 19846. - 432 с.
- Бондарь В.С., Абашев Д.Р., Петров В.К. Пластичность материалов при пропорциональных и непропорциональных циклических нагружениях // Вестник Пермского национального исследовательского политехнического университета. Механика. -2017. - № 3. - C. 53-74. DOI: 10.15593/perm.mech/2017.3.04
- Бондарь В.С., Абашев Д.Р. Некоторые особенности процессов монотонных и циклических нагружений. Эксперимент и моделирование // Вестник Пермского национального исследовательского политехнического университета. Механика. - 2019. -№ 2. - C. 25-34. DOI: 10.15593/perm.mech/2019.2.03
- Жермен П. Курс механики сплошных сред. Общая теория. - М.: Высшая школа, 1983. - 399 с.
- Зубчанинов В.Г. Механика сплошных деформируемых сред. - Тверь: Изд-во ТГТУ, ЧуДо, 2000. - 703 с.
- Ильюшин А.А. Пластичность. Основы общей математической теории. - М.: АН СССР, 1963. - 272 с.
- Койтер В.Д. Общие теоремы теории упруго-пластических сред. - М.: Изд. иностр. литературы, 1961. - 80 с.
- Можен Ж. Механика электромагнитных сплошных сред. - М.: Мир, 1991. - 560 с.
- Орлов А.Н. Введение в теорию дефектов в кристаллах. - М.: Высшая школа, 1983. - 144 с.
- Трусов П.В., Ашихмин В.Н., Швейкин А.И. Двухуровневая модель упругопластического деформирования поликристаллических материалов // Механика композиционных материалов и конструкций. - 2009. - Т. 15, № 3. - С. 327-344.
- Трусов П.В., Швейкин А.И. Теория пластичности. -Пермь: Изд-во Перм. национ. исслед. политехи. ун-та, 2011. - 419 с.
- Трусов П.В., Швейкин А.И. Многоуровневые модели моно- и поликристаллических материалов: теория, алгоритмы, примеры применения. - Новосибирск: Изд-во СО РАН, 2019. - 605 с. DOI: 10.15372/MULTILEVEL2019TPV
- Фридель Ж. Дислокации. - М.: Мир, 1967. - 644 с.
- Хирт Дж., Лоте И. Теория дислокаций. - М.: Атом-издат, 1972. - 600 с.
- Штремель М.А. Прочность сплавов. Ч. I. Дефекты решетки. - М.: Изд. МИСИС, 1999. - 384 с.
- Anand L. Single-crystal elasto-viscoplasticity: application to texture evolution in polycrystalline metals at large strains// Computer methods in applied mechanics and engineering. - 2004. -Vol. 193. - P. 5359-5383. DOI: 10.1016/ j.cma.2003. 12.068
- Ardeljan M., Beyerlein I.J., Knezevic M. A dislocation density based crystal plasticity finite element model: Application to a two-phase polycrystalline HCP/BCC composites // J. Mech. and Phys. Solids. - 2014. - Vol. 66. - P. 16-31. DOI: 10.1016/j.jmps. 2014.01.006
- Strain rate and temperature sensitive multi-level crystal plasticity model for large plastic deformation behavior: Application to AZ31 magnesium alloy / M. Ardeljan, I.J. Beyerlein, B.A. McWilliams, M. Knezevic // Int. J. Plasticity. - 2016. -Vol. 83. - P. 90-109. D01:10.1016/j.ijplas.2016.04.005
- Armstrong P.J., Frederick C.O. A mathematical representation of the multi axial bauschinger effect. CEGB Report RD/B/N 731, Central Electricity Generating Board. - 1966.
- Arsenlis A., Parks D.M. Modeling the evolution of crystallographic dislocation density in crystal plasticity // J. Mech. Physics Solids. - 2002. - Vol. 50. - P. 1979-2009. DOI: 10.1016/ S0022-5096(01)00134-X
- Balasubramanian S., Anand L. Plasticity of initially textured hexagonal polycrystals at high homologous temperatures: application to titanium // Acta Materialia. - 2002. - Vol. 50, iss. 1. -P. 133-148. DOI: 10.1016/S1359-6454(01)00326-3
- Benallal A., Marquis D. Constitutive equations for nonproportional cyclic elastoviscoplasticity // J. Engineering Materials and Technology. - 1987. - Vol. 109, no. 4. - P. 326-336. DOI: 10.1115/1.3225985
- Benallal A., Marquis D. Effects of non-proportional loadings in cyclic elasto-viscoplasticity: experimental, theoretical and numerical aspects // Engineering Computations. - 1988. -Vol. 5, iss 3. - P. 241-247. DOI: 10.1108/eb023742
- Benallal A., Le Gallo P., Marquis D. An experimental investigation of cyclic hardening of 316 stainless steel and of 2024 aluminium alloy under multiaxial loadings // Nuclear Engineering and Design. - 1989. - Vol. 114. - P. 345-353. DOI: 10.1016/0029-5493(89)90112-X
- Beyerlein I.J., McCabe R.J., Tome C.N. Effect of micro structure on the nucleation of deformation twins in polycrystalline high-purity magnesium: A multi-scale modeling study // J. Mech. Phys. Solids. - 2011. - Vol. 59. - P. 988-1003. DOI: 10.1016/j.jmps.2011.02.007
- Chaboche J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity // Int. J. Plasticity. - 1989. - Vol. 5, iss. 3. - P. 247-302. DOI: 10.1016/0749-6419(89)90015-6
- Doquet V., Pineau A. Extra hardening due to cyclic nonproportional loading of an austenitic stainless steel // Scripta Metallurgica et Materialia. - 1990. - Vol. 24, iss. 3. - P. 433-438. DOI: 10.1016/0956-716X(90)90178-J
- Doquet V. Twinning and multiaxial cyclic plasticity of a low stacking-fault-energy f.c.c. alloy // Acta Metallurgica et Materialia. - 1993. - Vol. 41, iss. 8. - P. 2451-2459. DOI: 10.1016/0956-7151(93)90325-M
- Fajoui J. et al. Micromechanical modelling of the elastoplastic behavior of metallic material under strain-path changes / Fajoui J., Gloaguen D., Courant B., Guillen R. // Comput. Mech. - 2009. - Vol.44. - P. 285-296. DOI: 10.1007/s00466-009-0374-7
- Feltner C.E., Laird C. Cyclic stress-strain response of f.c.c. metals and alloys-I. Phenomenological experiments // Acta metallurgica. - 1967a. - Vol. 15. - P. 1621-1632 DOI: 10.1016/0001-6160(67)90137-X
- Feltner C.E., Laird C. Cyclic stress-strain response of F.C.C. metals and alloys-II Dislocation structures and mechanisms // Acta metallurgica. - 1967b. - Vol. 15. - P. 1633-1653. DOI: 10.1016/0001-6160(67)90138-1
- Follansbee P.S, Kocks U.F. A constutive description of the deformation of copper based on the use of mechanical threshold stress as an internal state variable // Acta Metalls. -1988. - Vol. 36. - P. 81-93. DOI: 10.1016/0001-6160(88)90030-2
- Strain localization analysis using a multiscale model / G. Franz, F. Abed-Meraim, T. Ben Zineb, X. Lemoine, M. Ber-veiller // Comput. Materials Sci. - 2009. - Vol. 45. - P. 768-773. DOI: 10.1016/j.commatsci. 2008.05.033
- Frederick C.O., Armstrong P. A Mathematical representation of the multiaxial bauscinger effect // Materials at High Temperatures. - 2007. - Vol. 24, no. 1. - P. 1-26. DOI: 10.3184/096034007X207589
- Germain P., Nguyen Q., Suquet P. Continuum thermodynamics // J. Appl. Mech. - 1983. - Vol. 50. - P. 10101020. DOI: 10.1115/1.3167184
- Multiscale modeling of the plasticity in an aluminum single crystal / S. Groh, E.B. Marin, M.F. Horstemeyer, H.M. Zbib // Int. J. Plasticity. - 2009. - Vol. 25. - P. 1456-1473. DOI: 10.1016/ j.ijplas.2008.11.003
- Hamelin C.J., Diak B.J., Pilkey A.K. Multiscale modelling of the induced plastic anisotropy in bcc metals // Int. J. Plasticity. - 2011. - Vol. 27, iss. 8. - P. 1185-1202. DOI: 10.1016/j.ijplas.2011.01.003
- Haupt P., Kamlah M. Representation of cyclic hardening and softening properties using continuous variables // International Journal of Plasticity. - 1995. - Vol. 11, iss. 3. - P. 267-291. DOI: 10.1016/0749-6419(94)00049-2
- Horstemeyer M.F. Multiscale modeling: A review // In «Practical Aspects of Computational Chemistry». J. Leszczynski and M.K. Shukla (eds.). - Springer Science + Business Media B.V., 2009. - P. 87-135. DOI: 10.1007/978-90-481-2687-3_4
- Hu J., Cocks A.C.F. A multi-scale self-consistent model describing the lattice deformation in austenitic stainless steels // Int. J. Solids and Structures. - 2016. - Vol. 78-79. - P. 21-37. DOI: 10.1016/j.ijsolstr.2015.09.021
- Kocks U.F. Constitutive behavior based on crystal plasticity, In: Miller A.K. (eds): Unified Constitutive Equations for Creep and Plasticity. Dordrecht: Springer. - 1987. - P. 1-88. DOI: 10.1007/978-94-009-3439-9_1
- Laird C., Charsley P., Mughrabi H. Low energy dislocation structures produced by cyclic deformation // Materials Science and Engineering. - 1986. - Vol. 81. - P. 433-450. DOI: 10.1016/0025-5416(86)90281-8
- Lamba H.S., Sidebottom O.M. Cyclic plasticity for nonproportional paths: Part 1-Cyclic hardening, erasure of memory, and subsequent strain hardening experiments // J. Eng. Mater. Technol. - 1978. - Vol. 100, iss. 1. - P. 96-103. DOI: No.1 10.1115/1.3443456
- Simulation of polycrystal deformation with grain and grain boundary effects / H. Lim, M.G. Lee, J.H. Kim, B.L. Adams, R.H. Wagoner // Int. J. Plasticity. - 2011. - Vol. 27, iss. 9. -P. 1328-1354. DOI: 10.1016/j.ijplas. 2011.03.001
- Lin T.H. Analysis of elastic and plastic strains of a face -centered cubic crystal // J. Mech. Phys. Solids. - 1957. - Vol. 5, iss. 1. - P. 143-149. DOI: 10.1016/0022-5096(57)90058-3
- Ma A., Roters F., Raabe D. Studying the effect of grain boundaries in dislocation density based crystal-plasticity finite element simulations // Int. J. Solids and Structures. - 2006. - Vol. 43, iss. 24. -P. 7287-7303, DOI: 10.1016/j.ijsolstr.2006.07.006
- Maugin G.A. The saga of internal variables of state in continuum thermo-mechanics (1893-2013) // Mechanics Research Communications. - 2015. - Vol. 69. - P. 79-86. DOI: 10.1016/j.mechrescom. 2015.06.00.
- McDowell D.L. A nonlinear kinematic hardening theory for cyclic thermoplasticity and thermoviscoplasticity // Int. J. Plasticity. - 1992. - Vol. 8, iss.6. - P. 695-728. DOI: 10.1016/0749-6419(92)90024-7
- McDowell D.L. A perspective on trends in multiscale plasticity // Int. J. Plasticity. - 2010. - Vol. 26. - P. 1280-1309. DOI: 10.1016/j.ijplas.2010. 02.008
- Rice J.R. Inelastic constitutive relations for solids: an internal-variable theory and its application to metal plasticity // J. Mech. Phys. Solids. - 1971. - Vol. 19. - P. 433-455. DOI: 10.1016/0022-5096(71)90010-X
- Overview of constitutive laws, kinematics, homo-genization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications / F. Roters, P. Eisenlohr, L. Hantcherli, D.D. Tjahjanto, T.R. Bieler, D. Raabe // Acta Materialia. - 2010. - Vol. 58. - P. 1152-1211. DOI: 10.1016/j.actamat.2009.10.058.
- Roters F. Advanced material models for the crystal plasticity finite element method: Development of a general CPFEM framework. - RWTH Aachen: Aachen, 2011. -226 p.
- Tanaka E., Murakami S., Ooka M. Effects of plastic strain amplitudes on non-proportional cyclic plasticity // Acta Mechanica. -1985 - Vol. 57. - P. 167-182. DOI: 10.1007/BF01176916
- Taylor G.I. Plastic strain in metals // J. Inst. Metals. -1938. - Vol. 62. - P. 307-324.
- Tinga T., Brekelmans W.A.M., Geers M.G.D. A strain-gradient crystal plasticity framework for single crystal nickelbased superalloys // Report National Aerospace Laboratory. -Amsterdam, 2005. - 35 p. DOI: 10.1080/14786430802337089
- Trampczynski W. The experimental verification of the evolution of kinematic and isotropic hardening in cyclic plasticity // J. Mechanics and Physics of Solids. - 1988. - Vol. 36, iss. 4. -P. 417-441. DOI: 10.1016/0022-5096(88)90026-9
- Multilevel models of polycrystalline metals: Application for cyclic loading description / P.V. Trusov, P.S. Volegov, A.I. Shveykin, D.S. Gribov // Solid State Phenomena. - 2016. - Vol. 243. - P. 155-162. DOI 10.4028/www.scientific.net/SSP.243.155
- Xia Z., Ellyin F. Nonproportional Multiaxial Cyclic Loading: Experiments and Constitute Modeling // J. Appl. Mech. -1991. - Vol. 58, no. 2. - P. 317-325. D0I:/10.1115/1.2897188


