Три стадии старения человека как регулирование в системе энергетического обмена

Введение. Проблема старения актуальна и в медицинских, и в социальных аспектах. Одной из первых моделей, описывающих процессы старения, является классическая модель Гомпертца. Согласно обобщающему ее закону Гомпертца-Мейкхама, смертность является суммой компонент, зависящих и не зависящих от возраста. При этом компонент Гомпертца экспоненциально возрастает с возрастом и описывает процесс старения. Модель Гомпертца-Мейкхама можно условно отнести к классу механистических моделей, поскольку она основана на предположении об износе в терминах идеализированной «жизнеспособности».

Например, в [Иваницкий, Кринский, Сельков 1978: 77] старение организма рассматривается в рамках энергетического метаболизма и исследуется зависимость стационарной концентрации АТФ от активности обобщенной АТФазы, при этом утверждается, что за регулирование энергетического метаболизма отвечает гистерезис. В [Бутов, Санников 2002: 171] рассматривается система процессов энергетического обмена. В этих моделях реакцией на недостаточность энергии выступает повышение артериального давления. Согласно последним исследованиям, старение человека происходит в три этапа и связано с изменением качественного состава крови.

В описываемой работе предлагается математическая и имитационная модели системы энергетического обмена, характеризующего процесс старения живого организма. Авторы исходят из того, что изменения, которые провоцируют переход с одной на другую стадию старения, происходят тогда, когда энергетических ресурсов в организме меньше, чем потребностей. Графики, приведенные в данной работе, являются результатами имитационного моделирования» [Бурмистрова 2012].

Математическое описание структуры системы энергетического обмена. В работе рассматриваются процессы: концентрация триглицеридов, энергетические ресурсы, энергетическая потребность организма, уровень стресса, пороговая функция для алло-статической нагрузки, концентрация свободных радикалов [Бурмистрова 2012].

Пусть процесс g = ( g , ) ₍ > ₀ характеризует долю вырабатываемой объектом энергии. Предполагается, что g = ( g t ) >  _о процесс типа Орнштейна-Уленбека:

dgt= Ar (g-g,- ®, > + ^g.d^, g0 = 0, где ц - параметры модели, 71 определяет величину дисперсии случайного возмущения, и W1 = (Wt1)t>о - стандартный винеровский процесс, ®=(®,),>о - пороговая функция для аллостатической нагрузки, которая будет описана ниже, g – усредненная потребность энергии в течение суток, 7 - характеристика возмущений.

Изменение доли энергетических ресурсов в течение жизни ( n = ( nt ) t > 0 ) записывается как процесс:

процессы n = ( n, )_t > 0 и l = ( l, )_t >₀ будут описаны ниже.

Момент TQ - момент времени, когда энергетических затрат больше, чем имеется энергетических ресурсов (рисунок 1.) для внестрессового функционирования (без пере ходов в «форсированный режим») (TQ <да P - г л.):

т® = minp: / > 0: | g^ - и^ | > о|

Другими словами, в момент _T Q объект переходит в стрессовое состояние. «Аккумуляция» вызванных стрессами изменений (т. е. накопление аллостатической нагрузки) происходит, когда            . В моменты, когда аллостатическая нагрузка

(интеграл от               ) превысит пороговое состояние, объекту необходимо или исключить «стресс», или адаптироваться к этой ситуации. При адаптации в организме может, например, измениться поведение некоторых физиологических процессов [Бутов, Санников 2002: 171]. В настоящей работе адаптация происходит как одномоментное изменение вырабатываемой энергии и концентрации триглицеридов [Бурмистрова 2012]. Момент, когда адаптация в организме произойдет, будет определять начало новой стадии ста- рения. На рисунке 1 можно увидеть изменения энергетических ресурсов и затрат со временем.

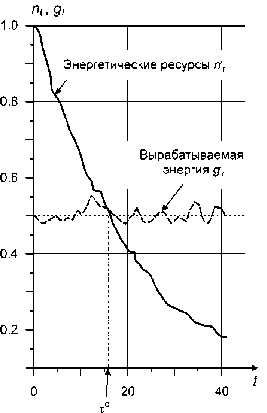
Рис. 1. Система взаимодействия энергетических ресурсов и потребностей (tQ – момент перехода в стрессовое состояние или «возможный» момент перехода на другую стадию старения).

Предполагается, что пороговая функция для аллостатиче-ской нагрузки ® = ⁽® ,, > о (впервые встретившаяся в формуле (1)), определяется как:

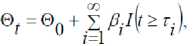
где

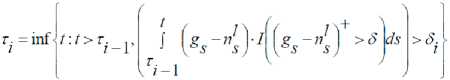
В моменты т. происходит адаптация организма к энергетическому стрессу, где i = 1,2,3,...., р. - параметры модели и определяются в ходе настройки модели. В момент t уровень вырабатываемой энергии снижается на величину р„

В модели, процесс f = ( f ) , >0 - уровень стресса, вызванный недостаточностью энергетических ресурсов [Дильман 1987], определяется как:

где коэффициент у - индивидуальный параметр объекта, который характеризует реакцию организма на стресс, вызванный недостаточностью энергетических ресурсов

[Бурмистрова 2012].

Предполагается, что количество митохондрий определяет выработку энергии внутри клетки [Николаев 1989]. С возрастом их количество заметно уменьшается (уменьшение может быть связано либо со старением, либо с гибелью клеток) и, согласно [Козинец 2000], убывает по экспоненте со стохастическим возмущением. Нормированное количество митохондрий (n = (n,) ) запишем со стохастическим дифференциалом:

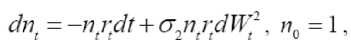
где W ² = ( w t ² ) _>o - стандартный винеровский процесс (не зависящий от W ¹) t > ₀ ), характеризует подключение к работе новых митохондрий или случайное отключение старых, коэффициент ^ ₂ - параметр модели.

На рисунке 2 показана кривая изменения доли митохондрий с возрастом.

Процесс ' = ( l ) t >0: оответствует динамике концентрации липидов (в первом приближении), (на рисунке 3 представлено первое приближение изменения динамики концентрации липидов с возрастом) которые с момента наступления i -й стрессовой ситуации, связанной с недостаточностью энергетических ресурсов, растут с коэффициентом a i

, г = 1,2,3,

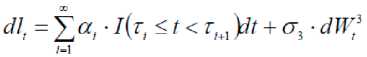
Предполагается, что при определении концентрации свободных радикалов r = ( r t ) t > ₀ ) нужно учитывать стресс, обеспечение энергетических потребностей, окисление липидов [Adachi, Ishii 2002: 487; Clancy, Gems, Hafen, Leevers, Partridge 2002: 296; Nordmann,Riviere, Rouach 1992:219].Процесс r = ( r ) t > ₀ определяется как:

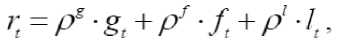
Коэффициенты Р⁸ , р f , р характеризуют

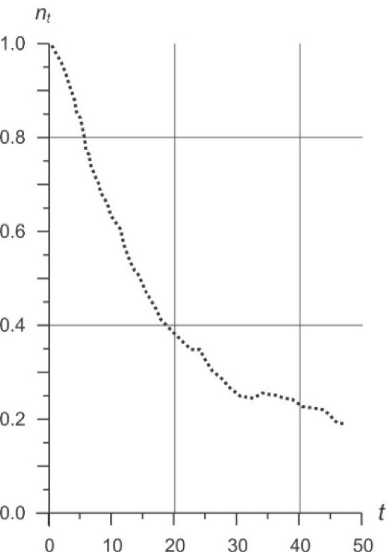
Рис. 2. Изменение доли митохондрий со временем (процесс n=(nt)t³0)

среднее время задержки реакции организма на энергетические потребности организма, на стресс, на окисление триглицеридов соответственно.

На рисунке 3 показана ситуация, когда объект, как компенсацию, изменяет динамику концентрации липидов; на рисунке 4 – снижение выработки энергии и переход на другую стадию старения.

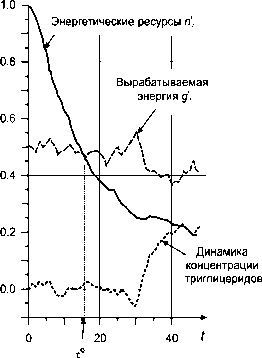
Рис. 3. Система метаболического обмена организма с повышением концентрации триглицеридов

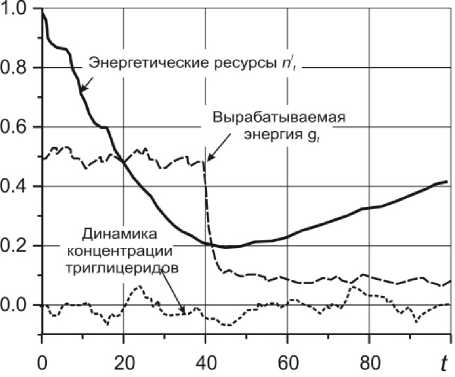
Рис. 4. Система метаболического обмена со снижением уровня выработки энергии

Заключение . В результате проведенных исследований жизни идеализированного биологического объекта установлено, что старение организма неизбежно, связано со временем, стадиально, но переход с одной стадии старения на другую допускает коррекцию.