Триадно-кластерные модели типовых случайных антенн

Главным отличием теории случайных антенн (СА) от статистической теории антенн (СТА) является переход от понятия «случайная ошибка» применительно к амплитудам, фазам, пространственным координатам и временным сдвигам, которое является ключевым в СТА, к понятию «неопределенность знаний» лиц, принимающих решения (ЛПР), относительно исходных данных, необходимых для исследования СА [1-2]. Это наилучшим образом соответствует природе СА и онтологической модели ситуации (ОМС), формируемой ЛПР в процессе проводимых исследований [3-4]. Рассматривая уровни напряженности Е_М электрической составляющей электромагнитного поля (далее Е -поля) и Н_М магнитной со ставляющей ( Н -поля) в точке наблюдения М как результаты обобщенного суммирования случайных составляющих, мы приходим к задаче анализа последовательностей их случайных сумм в условиях применимости центральной предельной теоремы (ЦПТ) теории вероятностей (ТВ) – как в традиционном, так и в обобщенном виде [57]. В первом случае это приводит к нормальным предельным распределениям для Е_М и Н_М , во втором случае – к семейству одномерных устойчивых распределений, обобщающих нормальный закон.

Поэтому наиболее вероятной моделью неопределенности, которой располагает сегодня теории СА, можно считать устойчивый закон [5]. Однако при неуверенности в условиях применимости ЦПТ ТВ, а также при отсутствии информации об атрибутах и свойствах неопределенностей, связанных с СА, ЛПР приходится руководствоваться «принципом безразличия» и считать неизвестные параметры и характеристики СА подчиняющимися равномерному закону.

Мощным средством исследования СА является метод статистического имитационного моделирования (СИМ), использующий компьютерную технологию метода Монте-Карло [2; 8-10]. Однако исходные данные для проведения СИМ в рамках принятой ОМС, от достоверности и точности которых существенно зависят его результаты, могут быть получены эвристическим способом или экспериментальным путем. В обоих случаях методики получения и формы представления этих данных, во-первых, должны быть адаптированы к требованиям СИМ. Во-вторых, наряду с аналитическими средствами решения поставленных задач ОМС должна допускать применение стохастической комбинаторики при построении адекватных реальности моделей СА методом СИМ.

В [11-12] на основе разработанной ОМС предложен триадно-кластерный метод (ТКМ) построения моделей апертурной СА (далее ТКМ-модели АСА), а также распределенной в пространстве модели СА (далее РСА), базовым элементом которых является триадный элементарный излучатель (ТЭИ), в качестве наиболее важных для практики вариантов реализации СА. Цель статьи – анализ вариантов формулировки исходных условий и обсуждение методики исследования характеристик векторов Е - поля и Н -поля для ТКМ-моделей АСА и РСА, построенных на основе ТЭИ.

ОМС для исследования АСА

Типовой вариант реализации АСА [13-14] представляет собой решетку из трех прямоугольных плоских апертур с размерами l × h , удаленных друг от друга на расстояние d , как это показано на рис. 1. Данная решетка с размерами l = 1,5 м; h = 1,8 м; d = 0,5 м моделируют окна в офисном помещении на поверхности стены S_A , через которые происходит утечка конфиденциальной информации (КИ) [15]. Характеристики Е -поля и Н -поля АСА с учетом стохастической комбинаторики ТЭИ в ее составе (три из них условно показаны на рис. 1 отрезками утолщенных сплошных линий) – как при отсутствии, так и при наличии случайных ошибок (амплитудных, фазовых, геометрических и др.) – подлежат определению в заданных точках М_S ( x_s ; y_s ; z_s ) на поверхности S_М , удаленной на расстояние R ₀ от нее. В зависимости от соотношения между r и длиной волны Л к точка М_S может находиться как в зоне Френеля, так и в зоне Фраунгофера поля АСА.

По аналогии с моделью АСА, где базовым элементом является элемент Гюйгенса [13-15], исследование ТКМ-модели АСА на основе ТЭИ должно дать ответ на следующие вопросы:

– как влияет рабочая частота, координаты точки М_S и размеры АСА заданной конфигурации на распределения характеристик векторов Е -поля и Н -поля в пределах поверхности S_М – при отсутствии случайных ошибок, в квазиде-терминированных режимах максимально возможной и частично полной энергетики АСА;

– какими статистическими свойствами обладают уровни и угловые сферические координаты векторов Е -поля и Н -поля в точке М_S ( x_s ; y_s ; z_s ) – на разных частотах, при стохастиче-

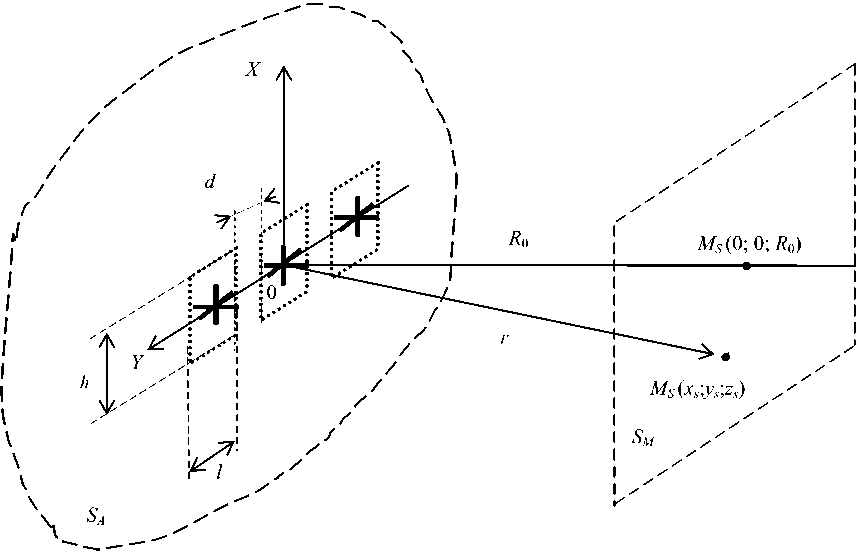
Рис. 1. Расположение трехэлементной АСА, состоящей из трех ТЭИ, в прямоугольной системе координат

ской комбинаторике ортогональных составляющих (ОС) этих векторов для ТКМ-модели АСА на основе ТЭИ;

– как влияют на указанные свойства случайные ошибки, сопровождающие работу АСА и учитываемые в рамках ее ТКМ-модели;

– как влияют на эти свойства корреляционные связи между ОС, а также между ошибками в рамках рассматриваемой ТКМ-модели АСА – учитываемые с помощью стохастической комбинаторики.

Также по аналогии с [13-15] будем считать, что атрибуты ТКМ-модели АСА (значения ошибок и «коммутирующих» компоненты ТЭИ параметров, разыгрываемые методом Монте-Карло) одинаковы в пределах одного корреляционного кластера и изменяются от кластера к кластеру случайным образом, независимо друг от друга.

Тогда следующим шагом для КИ-сигнала с дискретизированным энергетическим спектром, при длине волны Х^, соответствующей частоте Укл где k – номер гармоники, является определение размеров кластера D_K и линейного компонента ТЭИ l_k на частотах f_k в сверхшироких пределах: от 1 кГц и менее до 1 ГГц и более [15].

Границы зоны Френеля

0,62^D³/A_k2/A_k, (1)

где максимальный размер АСА по диагонали D = 5,8 м; расстояние r = 30 м, и тогда 134 МГц ≤ fk ≤ 3,6 ГГц. При этом на частотах ниже 134 МГц точка М_S находится в зоне Фраунгофера, тогда как на частотах выше 3,6 ГГц – в ближней зоне поля трехэлементной АСА.

Требования к модели ТЭИ

Длина линейного компонента ТЭИ в составе ТКМ-модели АСА должна удовлетворять условию 2л1_кЩ « 1 [16], что дает l_k < 0,016Л. . Таким образом, как относительный, так и абсолютный размеры l_k должны быть достаточно малыми (особенно последний на высоких частотах), то есть ТЭИ в данном случае действительно является элементарным источником. Но тогда и число ТЭИ в пределах кластера D_K , и число кластеров в пределах одной апертуры АСА или АСА в целом, в отличие от АСА, состоящей из элементов Гюйгенса [13-14; 17-18], определяются только условиями ее возбуждения в соответствии с корреляционными свойствами, которые предполагает разработанная ОМС.

С одной стороны, это упрощает процедуру СИМ, поскольку точечные ТЭИ располагаются лишь в узловых дискретных точках – в центре каждого кластера, тогда как элементы Гюйгенса непрерывно «выстилают» и каждый кластер, и поверхность АСА в целом, поэтому в [13-14; 17-18] на каждой частоте необходимо было рассчитывать их число и размеры.

С другой стороны, для определения D_K становится невозможно использовать какие-либо другие методы, кроме эвристических. Субъективные факторы, формирующие ОМС в условиях неопределенности знаний ЛПР об условиях работы АСА, при этом выходят на первый план – поскольку разные ЛПР могут иметь разные суждения по одному поводу.

Однако можно утверждать, что по мере роста числа источников КИ-сигнала, возбуждающих

АСА, а также с уменьшением ^-к число кластеров в пределах одной апертуры АСА будет возрастать: поэтому если на самых низких частотах в каждом кластере следует размещать по одному ТЭИ (как это показано на рис. 1), то затем необходимо увеличивать их число до 4 и, возможно, до 16. К счастью, метод СИМ позволяют исследовать последствия этого эффекта сравнительно просто [1-3; 17 и др.].

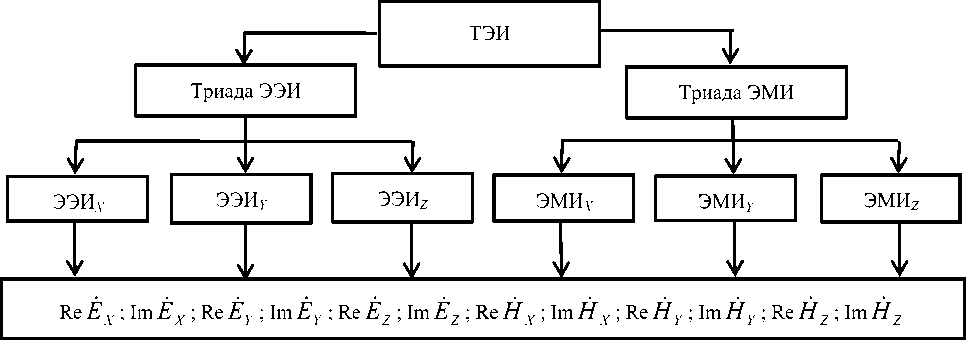
Рис. 2. Состав и структура £-поля и Н-поля ТЭИ [11-12]

Согласно [11-12], ТЭИ состоит из двух триад, показанных на рис. 2: первая триада образована ортогональными элементарными электрическими излучателями ЭЭИ _Х;Y;Z , вторая триада – аналогичными магнитными излучателями ЭМИ _Х;Y;Z . Из рис. 2 видно, что действительные и мнимые компоненты ОС образуют 12 массивов выходных расчетных данных, характеризующих свойства векторов Е -поля и Н -поля ТЭИ. Неопределенность конструкции и режима работы СА при этом моделируется путем комбинирования от 1 до 6 элементов ЭЭИ _Х;Y;Z и ЭМИ _Х;Y;Z , «включенных» случайным образом, а также при необходимости – амплитуд токов, возбуждающих их.

Это ведет к «разыгрыванию» методом Монте-Карло 8x8 – 1 = 63 вариантов сочетаний ЭЭИХ;Y;Z и ЭМИХ;Y;Z, так как случай их одновременного отсутствия в составе ТКМ-модели исключается. Данный подход соответствует максимальной неопределенности знаний ЛПР – когда, в соответствии с принципом безразличия, все возможные варианты состава АСА считаются равновероятными. В представленном виде ТЭИ является «стохастическим кирпичиком», из множества которых легко сложить ТКМ-модель (как статическую, так и динамическую) АСА и РСА практически любого вида и любой конструкции.

Типовой моделью АСА в виде дверей и окон является совокупность ТЭИ, расположенных на плоской поверхности S_A , как это показано на рис. 3, и возбуждаемых источниками КИ-сигнала, расположенными слева от АСА (в области Z < 0) [13; 15]. Если считать, что ось Z является внешней нормалью к АСА, то единственный продольный слой в ТКМ-мо-дели образуют элементы ЭЭИ _Z и ЭМИ _Z (при N_Z = 1 согласно обозначениям рис. 2), тогда как число поперечных элементов ТЭИ N_X и N_Y , ориентированных, соответственно, вдоль осей X и Y , определяется числом кластеров (выделенных на апертуре АСА штриховыми линиями – см. рис. 3) и может быть существенно большим. Общее число ТЭИ, очевидно, при этом есть N = N_X × N_Y . Представленная ОМС позволяет найти поле в точке перехвата КИ-сигнала по принципу Гюйгенса-Кирхгофа в два этапа: решить сначала внутреннюю задачу СТА [12], определив поля и виртуальные токи, возбуждающие АСА, а затем – внешнюю задачу с помощью метода СИМ [13-15].

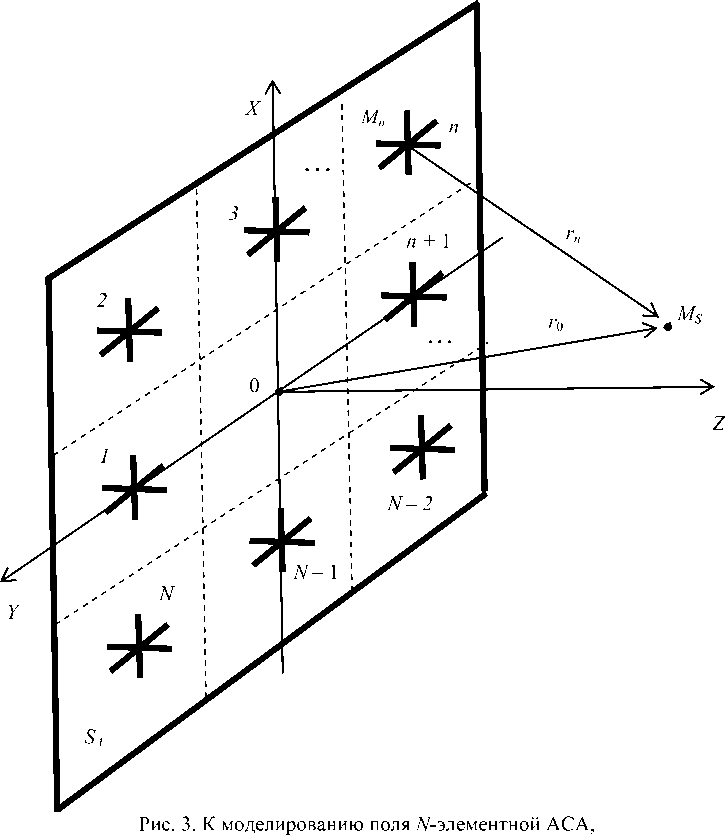
состоящей из ТЭИ

Особенности моделирования РСА

В качестве ТКМ-модели РСА, в отличие от АСА, может быть принята трехмерная система ТЭИ, состоящая из N = NX × NY × NZ элементов, совокупность которых соответствует области VS, где могут находиться источники КИ-сигнала, как это показано на рис. 4. Если считать, что Е-поле и Н-поле источников, которые формируют сигнал в точке перехвата КИ, присутствует во всем объеме помещения, то область пространства VS, заполненная N элементами ТКМ-модели РСА, представляет собой весь объем этого помещения. Если принять, что источники (особенно на низких частотах) находятся в пределах этажа офисного здания, или даже в пределах многоэтажного здания целиком, то объем VS на рис. 4 будет соответствующим образом возрастать. Процедура моделирования при этом не усложняется, но правомерность применения и возможно- сти такой модели нуждаются в более подробном обосновании.

Во-первых, ЛПР необходимо постулировать применение в рамках СТА трехмерного аналога принципа Гюйгенса-Кирхгофа, чтобы, как это было при исследовании АСА, сначала решить внутреннюю задачу, определив виртуальные токи, возбуждающие ТЭИ (см. рис. 4), а затем – внешнюю задачу определения характеристик Е - поля и Н -поля в точке М_S методом СИМ. Во-вторых, оговорить методику определения указанных токов, поскольку поверхностей волнового фронта, где они обычно вводятся, здесь нет. В-третьих, установить конкретные способы определения характеристик Е -поля и Н -поля – как в объеме V_S , так и в точке М_S – выбранным расчетно-экспериментальным или эвристическим (экспертным) путем, с учетом использования принципа взаимности при исследовании параметров Е -поля и Н -поля по аналогии с [13-15].

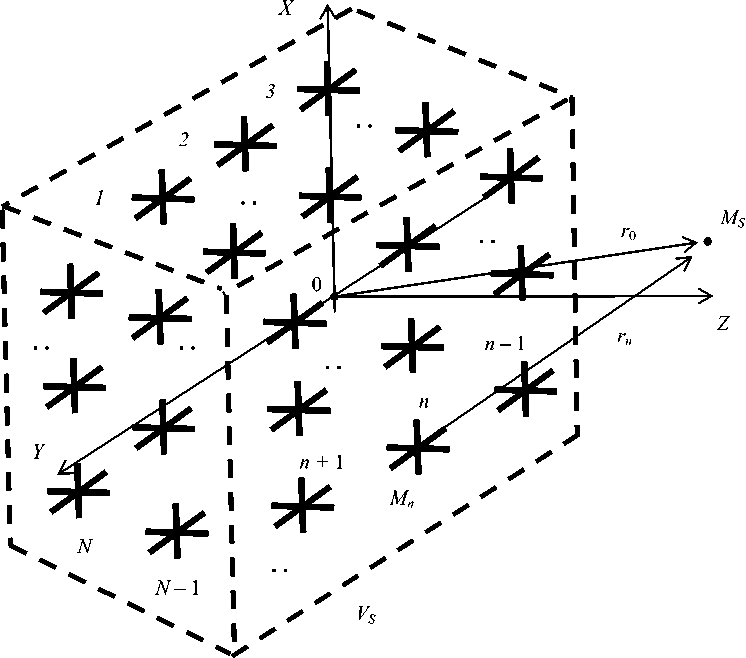
Рис. 4. К моделированию поля PC А, состоящей из ТЭИ

Относительно трехмерного аналога принципа Гюйгенса-Кирхгофа сошлемся на имеющийся прецедент: успешное применение С.А. Щел-куновым данного принципа при моделировании традиционных апертурных антенн – зеркальных, рупорных и т.п. [19]. Уже в этих моделях, строго говоря, базовый излучающий элемент не является источником Гюйгенса, а представляет собой часть ТЭИ – если учитывать амплитудные и фазовые искажения, а также кросс-поляризацию. Поэтому ТКМ-модели АСА и РСА представляются вполне логичным последующим шагом в данном направлении. Вопросы моделирования полей и эквивалентных токов в объеме V_S рассмотрим более подробно.

Токи, возбуждающие ТЭИ

Токи в объеме V_S могут быть определены по комплексным амплитудам векторов Е -поля и Н - поля из следующих соображений. Согласно [20], плотности эквивалентных электрического и магнитного токов на виртуальной поверхности S_П следуют из векторных произведений нормали к этой поверхности на векторы Н -поля и Е -поля в точке с декартовыми коорд и натами x ; y ; z , находящейся на этой поверхности:

как это показано на рис. 5 для . Поскольку взаимное расположение источников КИ-сигнала и точки, где определяются токи, ЛПР неизвестно, в общем случае случайные векторы          создают токи на поверхности с неизвестной конфигурацией.

Однако если информация об ОС указанных векторов                  получена, неопреде ленность знаний ЛПР касается только расположения поверхности SП, которую можно учесть, задавая единичную нормаль к ней как где углы являются стохастическими величинами. Отметим, что для рассматриваемого КИ-сигнала с длиной волны комплексные амплитуды токов, возбуждающих ТЭИ, есть

Э;М

_ У Т^Э:М Г! Т^э-^М Т^э'-^М

— Ху I_Х  + У у 1у  + 2gl_z .

Эти виртуальные токи необходимо связать с ОС векторов реального поля и , характеристики которых могут быть определены, например, экспериментальным путем.

В [12] показано, что ОС эквивалентных токов в данном случае равны

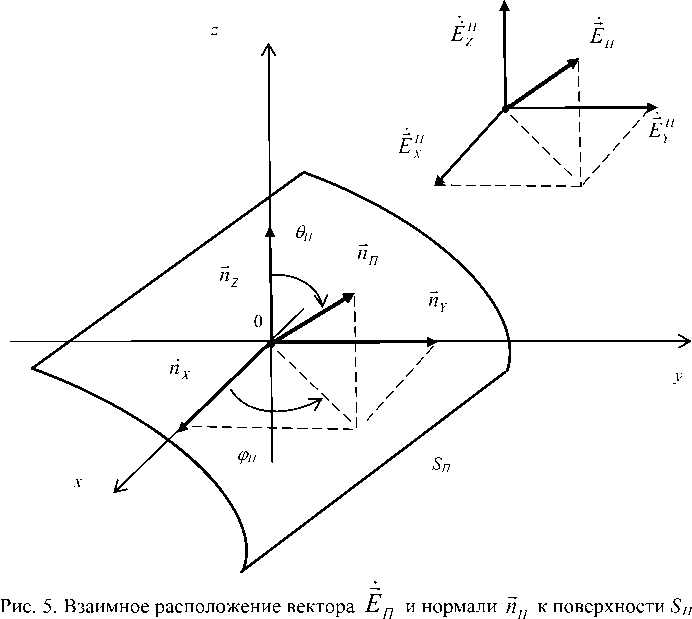
Р_х = (Ну sin ^_я sin 9_П - Ну cos 9_П ) А / _х ;

/у ~(Н_Х cos 9_П - Ну cos <р_п sin 9_П ) А Гу ;

Р_г = (Ну cos ф_п Гт9_п-Н" sin^sinУ_д)А/^ ;

р = (Ёу соъвд-ЁртфдКтвд^Уу ;      (4)

1у = р" cos ф_п sin 9_П - Ё” cos 6_П )М“ ;

Г г = (Ё" sin фп sin 9П - Ё" cos фп sin 9П ^М“,

где ^^ xy-.z – поперечные размеры компонентов ТЭИ с длинами ОС Г'У’-Z ’ нижние индексы k здесь и далее опущены.

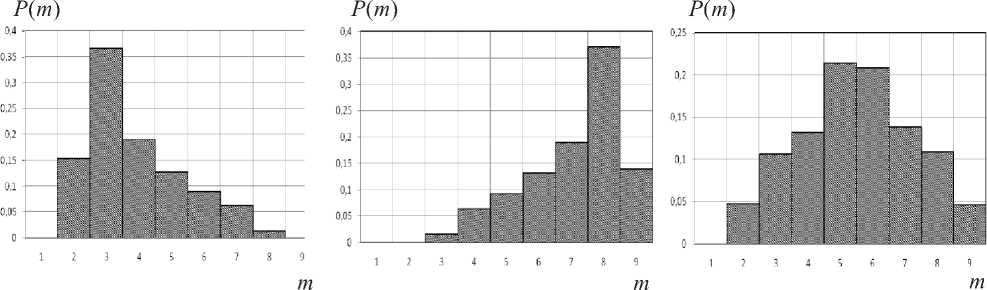
На основании принципа безразличия примем, что стохастические факторы ф_п [0; 360°]; 9_П [-90°; 90°], а также уровни ОС ^Ex.y.z [0,9; 1,1]; ^Е X.Y.Z [0,9; 1,1] распределены по равномерному закону. Воспользовавшись стандартной методикой СИМ [2; 8-9 и др.] при числе разыгрываний N_R = 10⁴, получаем гистограммы токов P\Y;Z ’ представленные на рис. 6, где на оси абсцисс указаны номера m [1; 9] одинаковых интервалов; на оси ординат – вероятности Р(т) попадания P;Y;Z [–1,6; 1,6] в эти интервалы. Отметим, что графики рис. 6а учитывают практически совпадающие при N_R >> 1 свойства 1^Э_Х и Гу ; рис. 6б – 1у И 1у ; рис. 6в – Iz ^и 1“ .

а)                                       б)                                       в)

Рис. 6. Гистограммы токов, возбуждающих ТЭИ при N_R = 10⁴:

а) 1_Х и 1_Y ; б) i_Y и 1_Х ; в) i_z и L_z

Данные рис. 6 иллюстрируют переход от «треугольного» распределения Симпсона к усеченному нормальному закону, отмеченный в [12]. При формировании ОМС с целью построения ТКМ-моделей АСА и РСА это обстоятельство необходимо учитывать, задавая распределения амплитудных ошибок. Фазовые ошибки токов I X;Y;Z ’ согласно (4), определяются ошибками ОС вектора токов X;Y;Z – ошибками ОС вектора ^X;Y;Z ’ которые, по нашему мнению, могут быть заданы только из эвристических соображений. В отношении геометрических ошибок и других виртуальных параметров, которые отражают неопределенность знаний ЛПР о структуре и режиме работы СА, ЛПР также приходится рассчитывать на эвристические методы.

Использование принципа взаимности при исследовании АСА и РСА

Экспериментально исследовать структуру Н - поля и Е -поля, что необходимо для моделирования АСА и РСА, можно двумя способами: в режиме излучения реального КИ-сигнала (см. рис. 7 а ) и в режиме приема тестового сигнала (см. рис. 7 б ). Причем в первом случае могут быть использованы как информационные (напрямую связанные с переносом КИ), так и информативные (характеризующие этот процесс косвенно) признаки КИ-сигналов, присутствующих в объеме V_S .

a)

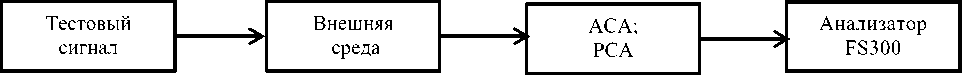
Рис. 7. Схема экспериментального исследования СА

а) в режиме излучения КИ-сигнала; 6) в режиме приема тестового сигнала

Во втором случае, особенно при исследовании РСА, на наш взгляд, следует использовать именно тестовые сигналы, близкие по информативным признакам к реальным КИ-сигналам, – поскольку фрагментами РСА в разные моменты времени могут быть самые разные элементы (провода, линии, блоки, устройства и т.п.) оборудования, размещенного в объеме V_S – как связанные с генерацией, обработкой и обменом КИ, так и не связанные с этими процессами, поэтому учесть особенности режима работы РСА на практике возможности нет.

Режиму излучения КИ-сигнала соответствует рис. 7 а : источники КИ в объеме V_S возбуждают АСА и РСА, создавая Е -поле и Н -поле, которые через внешнюю среду воздействует на точку М_S (см. рис. 3-4), где располагается аппаратура перехвата КИ. На рис. 7 б , напротив, тестовый сигнал через внешнюю среду воздействует на АСА и РСА, создавая в объеме V_S Е -поле и Н -поле, которые по принципу взаимности будем полагать близкими к полям на рис. 7 а ввиду того, что и АСА и РСА, и внешняя среда здесь одни и те же, а перемещаемый по объему V_S , анализатор спектра FS300 обеспечивает определение структуры

Е -поля и Н -поля во всех местах, где могут находиться источники КИ, что позволяет учесть сто-хастичность их свойств.

Таким образом, постулируется соответствие двух схем взаимодействия полей, создаваемых источниками КИ-сигнала, с внешней средой, АСА и РСА:

– «поле стохастической совокупности источников КИ-сигнала в объеме V_S – АСА и РСА – внешняя среда – поле плоской волны в точке М_S вблизи аппаратуры перехвата КИ» согласно рис. 7 а ;

– «поле тестового сигнала, который создает плоскую волну, воздействующую из точки М_S на объем V_S , – внешняя среда – АСА и РСА – измеритель уровней Е -поля и Н -поля во всех точках объема V_S » согласно рис. 7 б .

Задачей экспериментального исследования является формирование в рамках ОМС представления ЛПР о том, какими статистическими свойствами обладают структуры Е-поля и Н- поля в объеме VS , с целью подтверждения возможности принять данный объем в качестве ТКМ-модели РСА. Особенность предлагаемой методики состоит в том, что в режиме приема на частоте fk используется тестовый сигнал, близкий к КИ-сигналам по своим информативным признакам.

д)

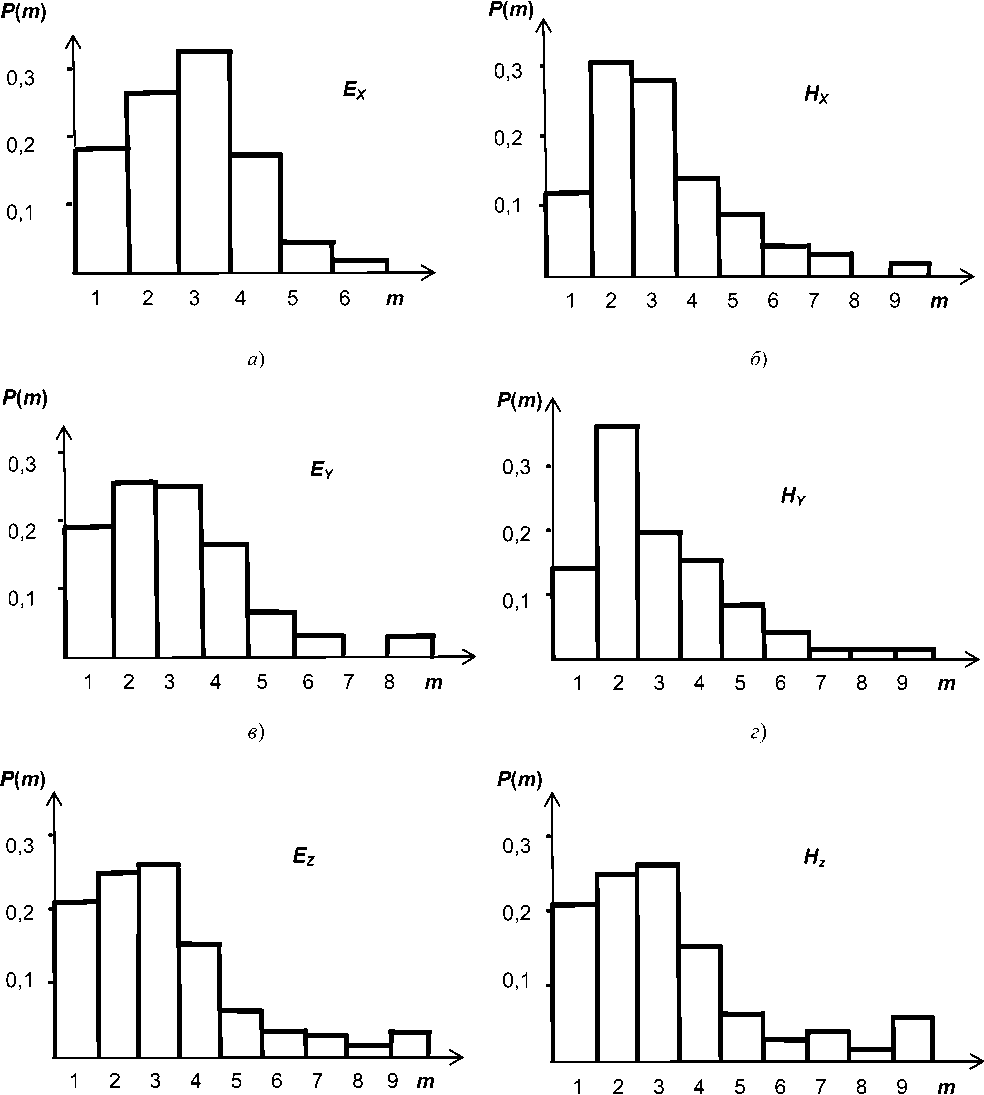
Рис. 8. Гистограммы ОС векторов /Г-поля и //-поля на частоте 49,75 МГц

Данные, аналогичные представленным на рис. 8, были получены также для ОС, модулей и сферических угловых координат векторов Е - поля и Н -поля при расположении точки М_S в том же помещении на высоте 1 м и 1,7 м от пола; на частотах 49,75 МГц и 56,25 МГц, общее число измерений 984.

Приведенные гистограммы демонстрируют как существенное отличие структуры Е -поля и Н -поля в объеме V_S от тестовой плоской волны, так и различия статистических свойств ОС ^X;Y;Z и ^X:i7 между собой. При этом установлено, во-первых, что поле КИ-сигнала в зоне Фраунгофера способен создавать источник КИ (с любыми пространственными координатами и любыми ОС) как Е -поля, так и Н -поля, расположенный в объеме V_S вблизи АСА и РСА. Во-вторых, что базовым элементом ТКМ-моделей АСА и РСА, адекватных такому источнику, может быть ТЭИ со структурой, соответствующей рис. 2. В-третьих, что если приемлемой ТКМ-моделью АСА является двумерный плоский слой ТЭИ на поверхности окон (см. рис. 3), то трехмерная ТКМ-модель РСА может представлять собой совокупно сть ТЭИ, заполняющих объем V_S полно стью (см. рис. 4). В-четвертых, что представленные на рис. 8 одновершинные гистограммы обладают до статочно ярко выраженными «тяжелыми хвостами», что говорит о применимости в данной ситуации условий обобщенной ЦПТ ТВ [3]. В-пятых, что сказанное, по нашему мнению, можно отнести ко всей пространственно-частотно-временной области возникновения электромагнитных каналов утечки КИ из офисного помещения во внешнюю среду [15].

Заключение

Представленная ОМС является основой для исследования характеристик АСА и РСА с помощью ТКМ. Предлагаемый в качестве базового компонента ТЭИ отличают простота и доступность использования в интересах СИМ, а также универсальный характер применения в составе ТКМ-моделей АСА и РСА. Фундаментом для исследования АСА и РСА методом СИМ являются принципы Гюйгенса-Кирхгофа, взаимности, безразличия и стохастической комбинаторики, адаптированные к методике ТКМ. Статистические свойства полей и токов, которые фигурируют в ТКМ-моделях АСА и РСА, соответствуют условиям применимости, обобщенной ЦПТ ТВ, – это обстоятельство необходимо учитывать при формулировке исходных условий для проведе- ния СИМ, на этапе выбора способа управления стохастической комбинаторикой в рамках ТКМ и законов распределения случайных ошибок. Результаты разработки ОМС позволяют приступить к непосредственному исследованию АСА и РСА методом СИМ.