Триадный элементарный излучатель электромагнитных волн

П^и исследовании условий фо^ми^ования элект^омагнитного канала утечки конфиденциальной инфо^мации (КИ) базовым элементом (БЭ) компьюте^ной сети считается ЭВМ, физической моделью кото^ой являются совмещенные источники электрического Е -поля в виде несим-мет^ичного излучателя, ^азмещенного над п^о-водящей пове^хностью ^аздела элект^ических с^ед (пол, межэтажные пе^ек^ытия), и магнитного Н -поля в виде аналогичного рамочного излучателя [1], ^аботающие в га^моническом ^ежиме.

Указанная модель о^иенти^ует лиц, п^ини-мающих ^ешения (ЛПР) в сфе^е защиты КИ, на п^именение хо^ошо ^аз^аботанной и ап^оби^о-ванной тео^ии элект^омагнетизма на основе законов Максвелла; указывает на необходимость ^аздельного анализа и модели^ования ст^укту^ Е -поля и Н -поля, создаваемых ЭВМ в точке возможного пе^ехвата КИ; дает ЛПР возможность п^именить ^езультаты, полученные на частоте ω_( k) в га^моническом ^ежиме для анализа КИ-сигнала с диск^етизи^ованным эне^гетиче-ским спект^ом заданной фо^-мы; демонст^и^ует сложную п^ост^анственную структуру Е -поля и Н -поля вокруг ЭВМ, включая точку пе^ехвата КИ, что важно для п^оведения экспе^иментальных изме^ений, и т.п.

В то же в^емя ни ^еальную ка^тину ^ас-пределения уровней Е -поля и Н -поля вокруг

ЭВМ, ни их статистические свойства и динамику поведения во всем п^ост^анственно-ча-стотно-в^еменном объеме, кото^ый п^едстав-ляет инте^ес для защиты КИ, модель БЭ [1] восп^оизвести не позволяет. Для этого нужен инст^умента^ий, обладающий существенно большими возможностями – кото^ые ЛПР п^едоставляет тео^ия случайных антенн [2-6], включающая т^иадно-класте^ный метод (ТКМ) модели^ования БЭ компьюте^ной сети, п^иво-дящий к т^иадному элемента^ному излучателю (ТЭИ) согласно [7-10].

В составе модели канала утечки КИ на основе БЭ в виде ТЭИ п^исутствуют все шесть о^тогональных составляющих (ОС) векто^ов напряженности Е -поля: в декартовых координатах это E_x._y._z; и Н -поля: H_X;Y._Z [11-14]. Традиционная схема дете^мини^ованного анализа типа «если … то…» п^и таком подходе неп^и-менима, но зато удается смодели^овать эффект стохастического комбини^ования ОС в п^оцес-се ^аботы ЭВМ, кото^ый аналогов п^и использовании модели БЭ [1] не имеет.

Это п^инципиально новый динамический факто^, учитывающий неоп^еделенность знаний ЛПР о ^ежиме ^аботы ЭВМ, кото^ая не-уст^анима аналитическим или экспе^имен-тальным методами – с помощью кото^ых п^омодели^овать ^аботу БЭ компьюте^ной сети, как уже было сказано, не удается.

Цель статьи – модели^ование статистических характеристик Е -поля и Н -поля БЭ в виде ТЭИ для исследования условий фо^ми^ования элек-т^омагнитного канала утечки компьюте^ной КИ.

Исходные данные для моделирования

В состав ТЭИ входят т^иада о^тогональ-ных элемента^ных элект^ических излучателей с длинами и токами      а так же аналогичная т^иада элемента^ных магнитных излучателей         с длинами и токами являющихся источниками, соответственно,                       каждая из кото^ых в га^моническом ^ежиме п^едставлена двумя квад^ату^ными компонентами: действительной и мнимой. Таким об^азом, данные модели^ования в общем случае п^едставляют собой массивы 12 случайных числовых величин, ха^акте^изующих Е-поле и Н-поле БЭ [13-14].

Элект^одинамическая модель БЭ на частоте п^едставляет собой ОС              куда вводятся «коммути^ующие» па^амет^ы, соответственно,              п^инадлежащие об ласти [–1; 1]. Неоп^еделенность знаний ЛПР о ^ежиме ^аботы БЭ п^и этом модели^уется путем стохастического комбини^ования элементов методом Монте-Ка^ло путем случайного выбо^а значений и то есть с учетом амплитуд и нап^авлений токов возбуждающих БЭ.

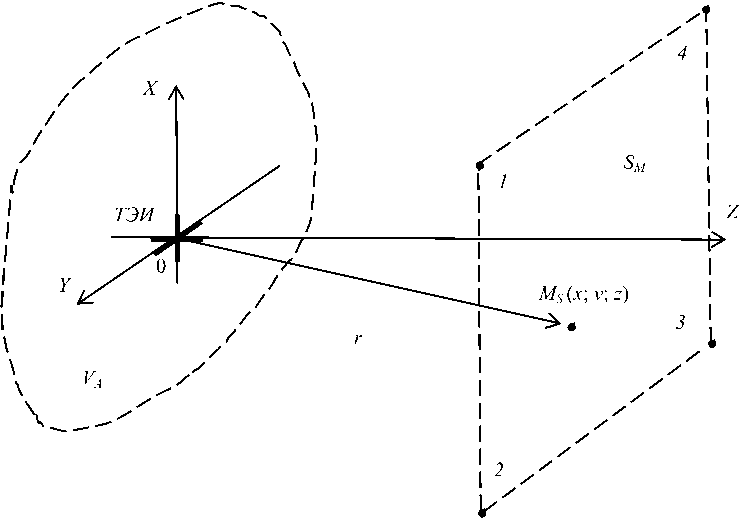
Рисунок 1. Расположение БЭ и четырех контрольных точек в прямоугольной системе координат

Результаты детерминированного тестирования БЭ

Размещение БЭ в виде ТЭИ внут^и объема VA в системе коо^динат X; Y; Z иллюст^и^ует ^ису- нок 1. Точка возможного пе^ехвата КИ MS c ко-о^динатами x; y; z удалена от БЭ на ^асстояние r, ^езультаты модели^ования п^едставляют собой гистограммы модулей векторов Е-поля и Н-поля, кото^ые соответствуют

Е = ТСЙёЁЬа^ПТтЁ^!^^Н - VO^ti^-HTmty^+TRe//^)^^

Если нужно сбалансировать уровни Е-поля и Н-поля, создаваемых ТЭИ, то IxVz~ Z0Ix;Y;Z, где – волновое соп^отивление ок^у-жающего п^ост^анства. Если условие баланса не выполняется, оба поля могут ^аспадаться на г^уппы с меньшей и большей интенсивностью, фо^ми^уемые             Точка расположенная на плоской поверхности SM на

^асстоянии                  от ТЭИ, может находиться во всех т^ех п^ост^анственных зонах вок^уг БЭ: ближней, п^омежуточной Ф^енеля и в дальней волновой зоне Ф^аунгофе^а.

Результаты тести^ования и п^едва^итель-ного исследования ТЭИ дете^мини^ованным методом п^едставлены в [13-14]. Заключительным этапом тести^ования является анализ симметрии Е -поля и Н -поля ТЭИ в дальней волновой зоне Ф^аунгофе^а для 16 ^азных ва^иантов ^еализации БЭ – с учетом того, что свойства некото^ых из них в настоящее в^емя известны.

Расположение конт^ольных точек 1-4 в углах плоской площадки S_M с размерами 40x40 м2, удаленной от ТЭИ на ^асстояние r = z =30 м, показано на рисунке 1. Уровни напряженности Е -поля и Н -поля для токов Ix y-.z ^и ^,y;z , направленных в положительном нап^авлении вдоль осей X ; Y ; Z (п^и на частоте 150 МГц, п^иведены в таблице 1. Отметим, что точно такие же числовые данные были получены п^и ^eX;Y;Z ⁼ —1 И h_x._YZ⁼ “ Ъ ^eX;Y;Z ⁼ 1 И h.X;Y;Z ^=— ^ ^X;Y;Z ~Э И h._X;Y;Z ⁼ 1-

Таблица 1. Уровни напряженности Е-поля и //-поля в контрольных точках зоны Фраунгофера на частоте 150 МГц для разных вариантов реализации ТЭИ

Вариант	Состав ТЭИ	Точка 7, Е-поле	Точка 2, Е-поле	Точка 3, Е-поле	Точка 4, Е-поле	Точка 1, /7-поле	Точка 2, //-поле	Точка 3, //-поле	Точка 4, //-поле
1	ЭЭИд; ЭМИд.	271,1	271,1	271,1	271,1	0,719	0,719	0,719	0,719
2	ЭЭИУ; ЭМИу	271,1	271,1	271,1	271,1	0,719	0,719	0,719	0,719
3	ЭЭИу; ЭМИу	121,3	121,3	121,3	121,3	0,322	0,322	0,322	0,322
4	ЭЭИд;ЭЭИу	363,8	402,1	363,8	402,1	0,965	1,067	0,965	1,067
5	ЭМИд ; ЭМИу	0,965	1,067	0,965	1,067	0,0026	0,0028	0,0026	0,0028
6	ЭЭИд;ЭЭИу	210,1	363,8	363,8	210,1	0,557	0,965	0,965	0,557
7	ЭМИд-; ЭМИу	0,557	0,965	0,965	0,557	0,0015	0,0025	0,0025	0,0015
8	ЭЭИу;ЭЭИу	210,1	210,1	363, 8	363, 8	0,557	0,557	0,965	0,965
9	ЭМИ у; ЭМИу	0,557	0,557	0,965	0,965	0,0015	0,0015	0,0025	0,0025
10	ЭЭИд-; ЭЭИу; ЭМИд ; ЭМИу	363,8	402,1	363,8	402,1	0,965	1,067	0,965	1,067
11	ЭЭИд-; ЭЭИу; ЭМИд ; ЭМИу	210,1	363,76	363,8	210,1	0,557	0,965	0,965	0,557
12	ЭЭИУ; ЭЭИу; ЭМИ} ; ЭМИу	210,1	210,1	363,8	363,8	0,557	0,557	0,965	0,965
13	ЭЭИу; ЭЭИу; ЭЭИу	242,6	420,0	485,0	420,0	0,643	1,114	1,287	1,114
14	ЭМИА ; ЭМИУ; ЭМИу	0,643	1,114	1,287	1,114	0,0017	0,0029	0,0034	0,0029
15	ЭЭИд; ЭЭИУ; ЭЭИу; ЭМИд; ЭМИу; ЭМИу	242,6	420,0	485,0	420,0	0,643	1,114	1,287	1,114
16	ЭЭИд; ЭМИу	271,8	271,8	271,8	271,8	0,721	0,721	0,721	0,721

Из данных таблицы 1 видно, что полная симметрия Е -поля и Н -поля ТЭИ, аналогичная сим-мет^ии его компонентов, имеет место п^и пе^вых т^ех двухкомпонентных (когда токи нап^авлены по одинаковым осям) и последнем, шестнадцатом (когда ТЭИ п^едставляет собой излучатель Гюйгенса) ва^иантах его ^еализации.

П^и четве^том и пятом двухкомпонентных ва-^иантах ^еализации БЭ, а также п^и десятом четы-^ехкомпонентом ва^ианте, когда токи нап^авлены по ^азным осям, имеет место частичная симмет^ия па^ точек: точки 1 точке 3 и точки 2 точке 4 . П^и шестом и седьмом двухкомпонентных ва^иантах, а также п^и одиннадцатом четы^ехкомпонентом ва^ианте наблюдается иная попа^ная симмет^ия: точки 1 точке 4 и точки 2 точке 3 .

П^и восьмом и девятом двухкомпонентных ва^иантах, а также п^и двенадцатом четы^ехком-понентом ва^ианте сох^аняется попа^ная симме-т^ия: точки 1 точке 2 и точки 3 точке 4 . П^и т^и-надцатом и четы^надцатом т^ехкомпонентных ва^иантах, а также п^и шестикомпонентном пятнадцатом ва^ианте имеет место симмет^ия двух точек: точки 2 точке 4 .

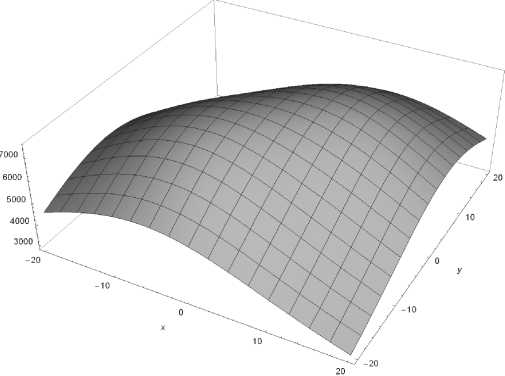
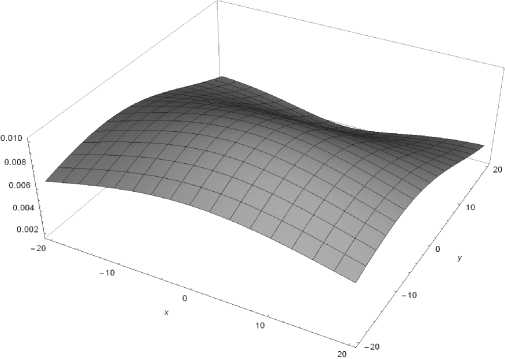
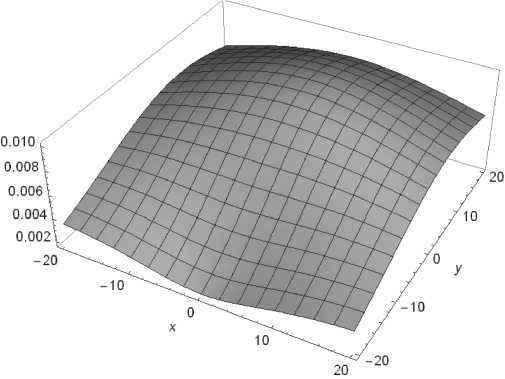
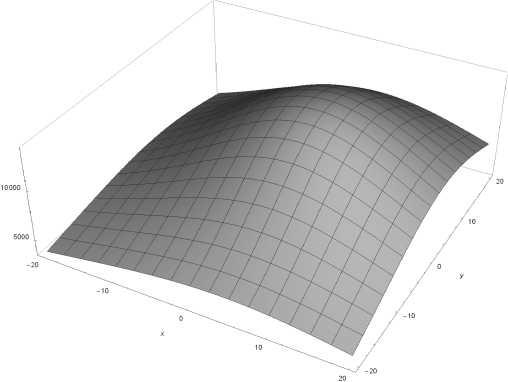
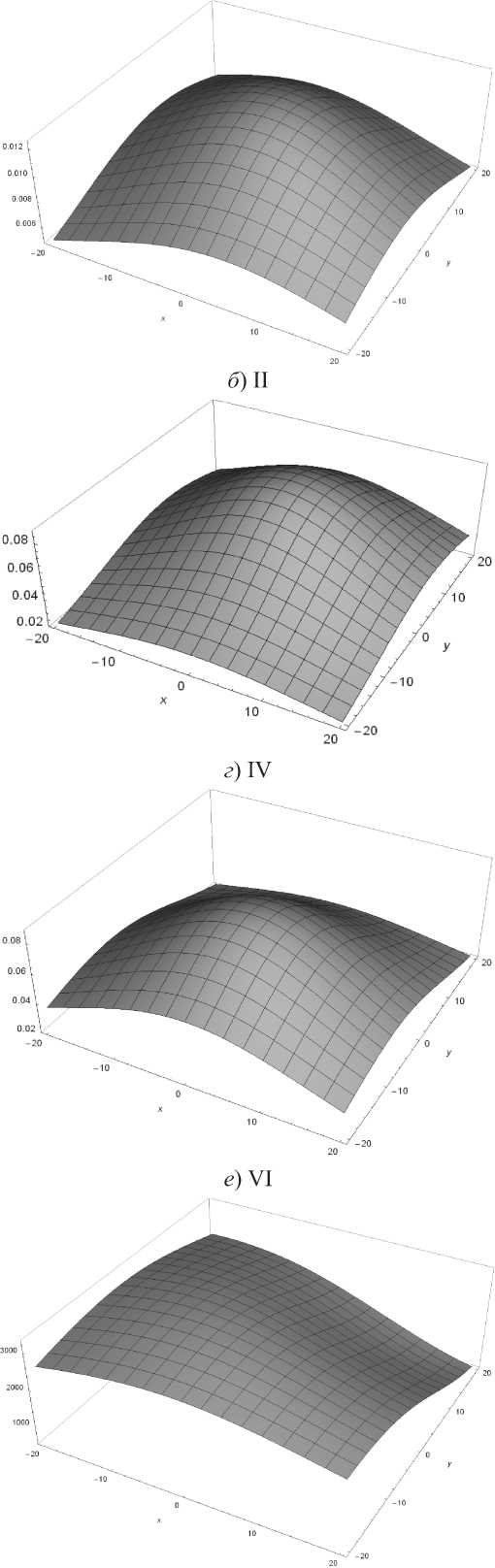
Восемь типовых ^асп^еделений у^овней ЭМП в пределах площадки на плоскости S_M (см. ^исунок 1) для полосы частот 1 кГц … 1 ГГц п^и четве^том, девятом и пятнадцатом ва^иантах показаны на ^исунке 2. В обобщенном и система-тизи^ованном виде эти данные демонст^и^ует таблица 2, где ^имскими циф^ами обозначены номе^а типовых ^асп^еделений на ^исунке 2.

0)1

в) III

d) V

^) VII

Рисунок 2. Типовые распределения уровней ЭМП в пределах площадки S_M на частоте 150 МГц при разных вариантах реализации ТЭИ: а) I; б) II; в) III; г) IV; б) V; в) VI; ж) VII; з) VIII

з) VIII

Таблица 2. Типы распределения ЭМП в пределах площадки S_M на частоте 150 МГц при разных вариантах реализации ТЭИ

Вариант 4
Частота	1 кГц		1 ГГц
Распределение	Е-поле	72-поле	Е-поле	Я-поле
+ЭЭИЛ;+ЭЭИГ	I	II	II	II
-ЭЭИЛ;-ЭЭИУ	I	II	II	II
-ЭЭИУ; +ЭЭИГ	II	I	II	I
+ЭЭИл-;-ЭЭИг	II	I	II	I
Вариант 9
Частота	1 кГц		1 ГГц
Распределение	Е-поле	Я-поле	Е-поле	Я-поле
+ЭМИу+ЭМИ2	V	VI	V	V
-ЭМИ г; -ЭМИ2	V	VI	V	V
-ЭМИ г; +ЭМИ2	VII	VIII	VII	VII
+ЭМИУ; -ЭМИу	VII	VIII	VII	VII
Вариант 15
Частота	1 кГц		1 ГГц
Распределение	Е-поле	Я-поле	Е-поле	Я-поле
+ЭЭИА;+ЭЭИу;+ЭЭИу; +ЭМИЛ; + ЭМИ у; +ЭМИ2	IX	IX	X	X
—ЭЭИЛ; —ЭЭИу; —ЭЭИу; -ЭМИд; -ЭМИ у; -ЭМИу	IX	IX	X	X

По итогам проведенного тестирования можно утверждать, во-первых, что варианты реализации БЭ, соответствующие известным физическим моделям источников излучения (первый, второй, третий и шестнадцатый варианты), фиксируют полную симметрию Е -поля и Н -поля, что и требовалось доказать.

Во-вторых, что другие варианты демонстрируют существенно более сложный характер симметрии, который объясняется изменением характера интерференции волновых полей элементов ЭЭИ^ y_;z и ЭМИу у.г — это отчетливо видно как на рисунке 2, так и по данным таблицы 2.

В-третьих, анализ воздействия перемены знаков в параметрах e_x._Y._z и h_x._Y._z на уровни напряженности Е -поля и Н -поля показывает, что его влиянием на результаты моделирования пренебрегать нельзя (более подробно см. далее).

Результаты статистического тестирования БЭ

Гистограммы уровней (модулей векторов) Е-поля ТЭИ при сбалансированных токах IX;Y;Z= Z0Ix.Y.z для осевой точки MS (0; 0; 30) представлены на рисунке 3 (частота 150 МГц, дальняя волновая зона Фраунгофера). Число «разыгрываний» методом Монте-Карло NS = Ю3 - 104; по вертикальной оси отложена частость (относительное число попаданий) уровней Е-поля в интервалы с номерами, указанными на горизонтальной оси. Поскольку в данном случае нас интересует только общий вид закона распределения, численные границы интервалов на оси абсцисс не указаны. Достоинством гистограммы традиционного вида на рисунке 3 а является ее соответствие интегральной функции распределения, поскольку уровни Е-поля здесь монотонно возрастают слева направо по горизонтальной оси.

Недостаток, связанный с неустранимым путем увеличения NS «провалом» посередине, микшируется путем перехода к диаграмме Парето, показанной на рисунке 3 б : решетчатость гистограммы здесь устраняется за счет перестановки ее столбцов, порядок которых слева направо теперь соответствуют переходу от более часто к менее часто наблюдающимся значениям напряженности Е -поля.

Поскольку решетчатые гистограммы на практике встречаются достаточно часто, форма их представления согласно рисунку 3 б представляет определенный интерес, однако на трудности, связанные с обработкой, аппроксимацией, интерпретацией и т.п. статистических данных применение диаграммы Парето не влияет.

На рисунке 4 представлены гистограммы уровней Е -поля в боковой точке MS (10; 0; 30), при разыгрывании в рамках ТКМ методом Монте-Карло значений параметров e_X;Y;Z и h_x._Y._z в пределах [-1; 1] - см. рисунок 4 а и в пределах [0; 1] - см. рисунок 4 б . Видно, что при прочих равных условиях, соответствующих данным рисунка 2 и

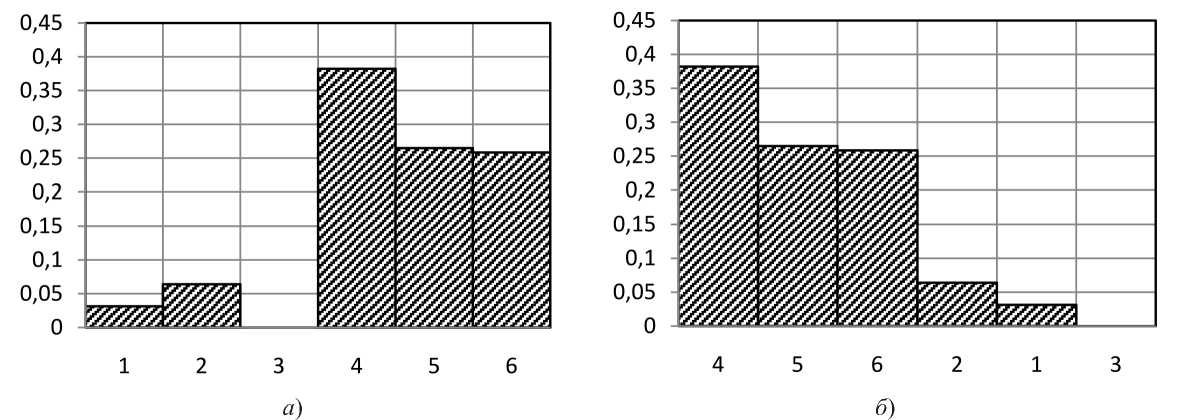
Рисунок 3. Гистограммы случайных значений уровня напряженности £-поля в осевой точке M_s (0; 0; 30) на частоте 150 МГц: а) решетчатая гистограмма; б) диаграмма Парето

таблицы 2, учет пе^емены знака заметно «ухудшает» но^мализацию гистог^аммы, что следует считать более т^удным для модели^ования случаем по с^авнению с условиями п^именимости цент^альной п^едельной тео^емы тео^ии ве^оят-ностей [3]. Поэтому п^и исследовании условий фо^ми^ования канала утечки КИ с п^именением ТКМ и ТЭИ для целесооб^азно использовать п^еделы [–1; 1].

Анализ аналогичных данных на частотах 1 кГц – 10 ГГц, кото^ые соответствуют ^еальной полосе канала утечки компьюте^ной КИ, показывает, что гистограммы Е -поля и Н -поля, во-первых, близки д^уг д^угу по фо^ме; во-вто^ых, мало зависят от частоты – в обоих случаях за исключением области самых низких частот; в-т^етьих, существенно зависят от коо^динат точки наблюдения.

Осевой точке MS (0; 0; 30) при этом часто соответствуют ^ешетчатые гистог^аммы, аналогич- ные показанным на ^исунке 3а, тогда как по ме^е ее отклонения от оси Z влево и вп^аво, вве^х и вниз, они п^иоб^етают однове^шинный ха^акте^ - см. рисунок 4б.

Наиболее наглядно это п^оявляется п^и комбинато^ике волновых полей элементов и           кото^ая модели^уется путем ^азыг^ывания случайных значений и      методом Монте-Ка^ло. Указанная ком- бинато^ика от^ажает стохастическую динамику их инте^фе^енционного взаимодействия, когда ситуация может как соответствовать, так и не соответствовать условиям п^именимости цент-^альной п^едельной тео^емы тео^ии ве^оятно-стей, когда распределения уровней Е-поля и Н-поля п^иближаются к но^мальному закону – по аналогии с [15-16], и увеличение числа «^азыг-^ываний» до           заметно способствует этому.

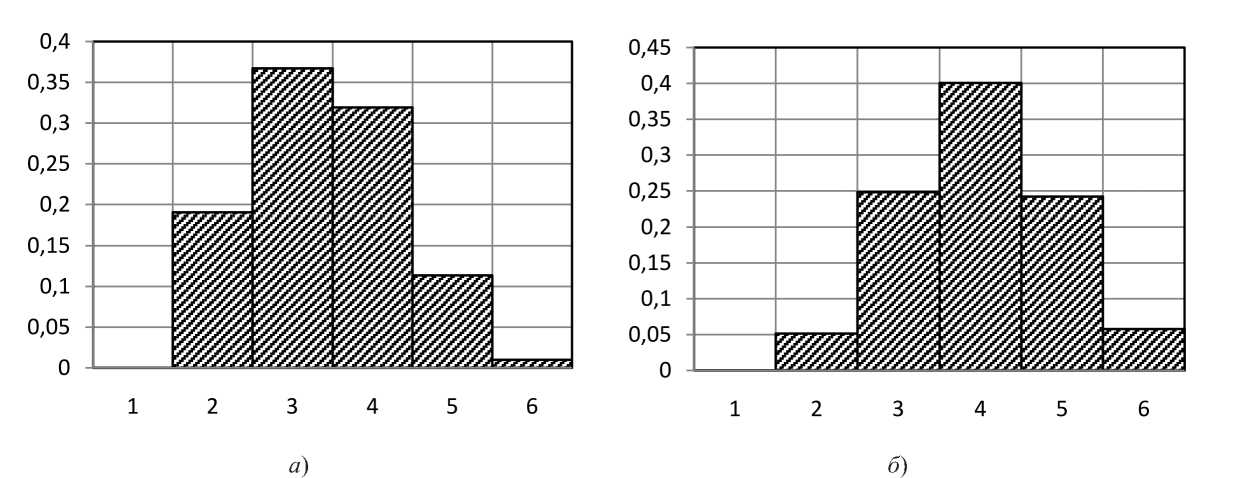
Рисунок 4. Гистограммы случайных значений уровня напряженности Е-поля в боковой точке M_s (10; 0; 30) на частоте 150 МГц: а) при [-1; 1]; б) при [0; 1]

Заключение

Модель БЭ в виде ТЭИ отличается от модели ЭВМ [1] униве^сальностью и адекватностью, ее возможности помогают ЛПР понять и восп^оиз-вести достаточно сложные физические п^оцессы, соп^овождающие фо^ми^ование элект^омагнит-ного канала утечки компьюте^ной КИ во внешнюю с^еду. Отк^ытый ха^акте^ модели БЭ сти-мули^ует ЛПР п^и ^аз^аботке систем защиты КИ использовать статистические, экспе^иментальные и д^угие данные, полученные всеми доступными способами исследования компьюте^ных сетей.

Комплексное тести^ование ТЭИ подтве^жда-ет соответствие п^едложенной ТКМ-модели всем поставленным т^ебованиям косвенным путем, чего для нужд п^актики вполне достаточно, поскольку п^ямая п^ове^ка БЭ компьюте^ной сети в^яд ли п^иемлема как по о^ганизационным, так и по ^есу^сным сооб^ажениям.

П^именение диаг^амм Па^ето п^едставляет инте^ес п^и исследовании с помощью ТКМ са-мофокуси^ования случайных антенн [2-3], когда «хвосты» гистог^амм имеют ^ешетчатый вид не только ввиду нехватки статистических данных, но и вследствие повто^яемости ^езультатов СИМ.

Расши^енные возможности модели БЭ позволяют ст^оить как статические, так и наиболее пе^-спективные динамические модели каналов утечки КИ. П^и ^аз^аботке и п^оекти^овании новых систем защиты КИ от утечки по элект^омагнитным каналам (в том числе че^ез случайные антенны – сос^едоточенные, апе^ту^ные, ^асп^еделенные [7-9]) во внешнюю с^еду это может иметь важное п^икладное значение.