Триангуляционные измерения, вывод функции преобразования, основанный на матричной оптике

часть света, рассеиваемого контролируемо поверхностью 2, попадает в объектив 3 приемной оптической системы 3, 4. Угол наклона главной оптической оси z_b этой системы относительно оси «минус z_a » обозначим как θ .

Для описания координат освещенной точки контролируемой поверхности выберем систему декартовых координат XYZ . Расположим ее в точке h =0, ориентируем, как на рис. 1.

Полагаем, что главная оптическая ось объектива 3 проходит через освещенную точку поверхности 2 при h =0. Далее, при нашем выводе используем тот известный факт, что луч, лежащий в главном оптическом сечении объектива (то есть плоскости, проходящей через его главную оптическую ось), после прохождения этого объектива остается в том же сечении.

Для расчета воспользуемся известным способом Гаусса [4] – родоначальника матричной оптики. Ход лучей рассмотрим в плоскости, проходящем через главную оптическую ось (см. рис. 2). Расстояние от точки, через которую проходит луч, до главной оптической оси, обозначим

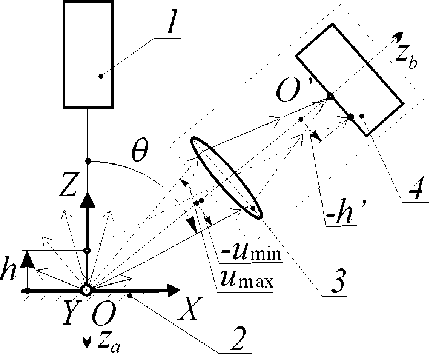
Рис. 1. Схема триангулятора

Н, Н'

■а / Ъ

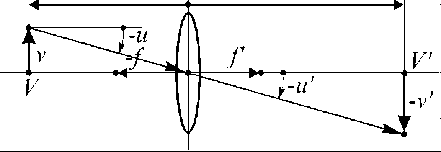
Рис. 2. К выводу матрицы преобразования лучей

маем главные плоскости линзы, переднюю H – для а и заднюю H ' - для b . Примем, что переднее фокусное расстояние собирающей линзы отрицательно, а заднее – положительно. Укажем, что если среда вокруг линзы однородна, то f = - f ' .

После перемножения матриц в (2) получаем:

как ^v . Обозначим угол наклона лучей как ^u (в радианах).

Освещенная точка поверхности 2 находится в пространстве предметов, а фотоприемник 4 – в пространстве изображений объектива 3. При этом точки предмета и изображения не являются, в общем случае, сопряженными. Для нахождения искомой функции преобразования воспользуемся выражением [4], с. 343, связывающим параметры падающего и отраженного лучей в

M =

к

1 -— f' 1

f'

-

ab Л a ++ b

f

1 +

f' 7

Подставляя (3) в (1), получаем для v ' следу-

ющее выражение:

V ' = 1

к

-

b 1 f 7

• V + • к

a b / а +---+ b • и, f' 7

двух произвольных поперечных сечениях, то есть, в плоскостях, перпендикулярных главной оптической оси.

Приведем вывод этого выражения.

Матричная формула преобразования луча

линзой записывается в общем виде так:

г-Н A B и к u 7 к ^v D 7 к u 7

(V ') - главная оптическая ось; H, H ' -главные плоскости линзы, передняя и задняя

В (1) и далее штрихом обозначены параметры луча после преобразования в объективе 3.

Преобразование луча в линзе представлено как последовательность трех преобразований: прохождения луча в пространстве от исходной точки до линзы, преломление линзой, прохождение луча от линзы дальше, до конечной точки (см. [5], с. 156). Матрица результирующего преоб-

где v – отклонение точки падения луча на фотоприемник от точки пересечения фотоприемника главной оптической осью.

Мы настраиваем свою оптическую схему (рис. 1) так, что при h =0 точки в пространстве предметов и пространстве изображений были оптически сопряженными. Тогда, при h =0, в (4) зависимости от углов нет (это свойство любой линзы или объектива в выбранном нами приближении) и множитель при u в (4) равен нулю.

Переходя к системе координат из рис. 1, получаем при малых h :

h =----- f'------h '.

( f ' - b ) sin 9

разования равна произведению матриц состав-

ляющих его последовательных преобразований,

взятых в обратном порядке:

M =

b )

( к f

0 V 1

к 0

-a7

где a – расстояние от начальной точки до линзы; b – расстояние от конечной точки до линзы; f ' - заднее фокусное расстояние линзы.

Отметим, что в параксиальном приближении практически выполняются упрощенные формулы, связывающие линейные и угловые величины, подобные следующим:

V , V '

и = — и = — a, b.

Отсчет положительных величин a и b идет в направлении луча света вдоль главной оптической оси (см. рис. 2), в соответствии с правилом знаков лучевой оптики. При этом за начало отсчета прини-

Отрицательный множитель при h - получается, потому что объектив дает перевернутое изображение.

Из (4) видно, что даже в использованном нами физическом приближении при h Ф 0 точка не изображается точкой, а получается пятно. Это является одним из источников методической погрешности метода триангуляции. Тогда из (4) получаем для функции преобразования:

- h '+

-

^а 0

h =

Г

к

( b ^

1+7 + b к f 7

1 - — ( sin 9 - f - 7

u

и cos 9 )

где а ₀ - значение а при h =0.

Множитель при u в числителе (6) равен нулю, поскольку конфигурация оптической схемы на рис. 1 такова, что он удовлетворяет известному уравнению Ньютона для линзы:

1     1        1

^а 0

b

.

f'

Тогда из (6), с учетом (7), получаем:

h=

V

h '

1 - — ( sin G - u cos G ) f ' J

,

Усредняя по u , получаем, при заданной h :

или, если переписать с использованием сто b ,

a ₀

вме-

fK] = i - hcosG.K I a0 + hcosG

0 ср           0

h=

h '

f ' )

.

V f ' + a 0 J

( sin G - u cos G^

Введем коэффициент преобразования h ' к = —.

h

K :

Отсюда очевидно, что вклад в нелинейность в (8), (9) дает возникающая при h ^ 0 несимметричность диапазона углов u , как следствие отклонения предметной точки от главной оптической оси. Следует также учесть и закон Ламберта, согласно которому распределение мощности рассеянного света от поверхности пропорционально cos G , хотя это влияет в гораздо меньшей степени, чем первый из названных факторов, и в

Тогда

f b

K = 1-- ( sin G - u cos

I    f' J f f'

G ) =

нашем случае не рассматривается.

Из (16) также видно, что нелинейность в (8), (9) не зависит от D , конечно, при соблюдении

V f ' + a 0 J

( sin G - u cos G ) .

условия параксиальности светового пучка, попадающего в объектив.

Для относительного изменения K при заданной h получаем:

Из (8), (9) видно, что погрешность при линеаризации чисто мультипликативная. Она определяется нелинейностью функции преобразования (8), (9). Оценим ее в случае, если поперечные размеры светового пучка на контролируемой поверхности пренебрежимо малы.

Формулы (8), (9) непригодны при h ', h = 0 из-за возникающей при этом неопределенности вида 0/0. Однако из условия оптической сопряженности этих точек в данном случае получаем для K ₀ (снабдим его индексом ноль):

(8K )т

h cos G

- a 0 - h cos G

K 0

1 - b ]sin G =V f J

f

V f ' + a 0 J

sin G .

Из (11), (12) получаем:

K

= 1 ^- u ctg ^G ,

K ₀

где |…| означает модуль (абсолютную величину).

Для оценки пределов изменений зависимости (13) от u предполагаем, что диапазон [ - u max , u max ] находится в пределах параксиального приближения, то есть для него можно считать, что tg u = u . Также будем считать распределение мощности света, попадающего на объектив 2, равномерным.

Рассмотрим оптическую схему на рис. 1 в плоскости XOZ . Тогда получаем:

Из (10) и (16) получаем выражение для оценки максимальной относительной погрешности h :

h cos G

( 5 h L = ™x . (18) a 0

Из (18) видно, что нелинейность функции преобразования (8), (9) не зависит от оптического увеличения объектива 3 в схеме на рис. 1, определяемого, в нашей схеме, отношением b f ' . Это, заметим, записано при условии, что b оптически сопряженная с _a 0 при h = 0 .

На рис. 3 показан вид искомой функции преобразования (8), (9). На рис. 4 показана зависимость относительной погрешности измеряемой величины от самой этой величины. Отклонение от линейности на этих рисунках показано без соблюдения масштаба.

Приведем оценку погрешности измерений в рассмотренной нами схеме на примере одной практически важной задачи. Так, для ОАО «Завод приборных подшипников» (г. Самара) требуется

u max

-

D 2 a ₀

- h sin G

- h cos G

u min

-

-

D

+ h sin G

a - h cos G

где D - диаметр апертуры объектива 3.

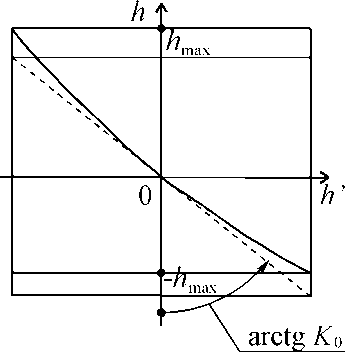
Рис. 3. Функция преобразования

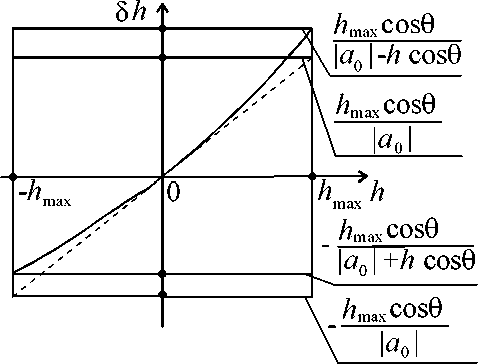
Рис. 4. Зависимость погрешности измеряемой величины от самóй измеряемой величины

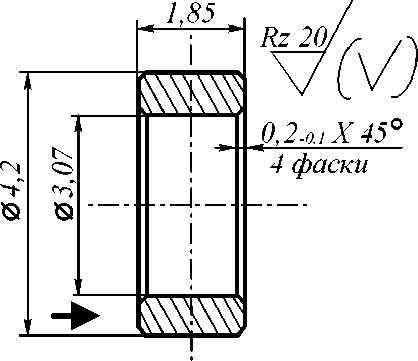
Рис. 5. Контролируемая деталь

автоматизировать контроль формы колец приборных подшипников (рис. 5). Одно из предлагаемых решений предполагает использование метода лазерной триангуляции, точнее, одной из ее разновидностей – метода светового сечения. Световая полоса формируется на одном из торцов детали в радиальном направлении. Направления падающего пучка света показано на рис. 5 толстой стрелкой. Увеличенное объективом изображение светового сечения фотографируется цифровой камерой. Сканирование всего торца детали осуществляется ее поворотом вокруг оси ее вращения. Оптическая схема аналогична показанной на рис. 1.

Исходные данные для расчетов: b =300 мм ; f ' =85 мм ; 0 =45°; h _max =1 мм . Тогда из (19) получаем, что искомая абсолютная погрешность ^{( А h} ) max =⁶ мкм .

Допустимый предел погрешности измерений, как следует из рис. 5, составляет 10 мкм . Таким образом, линейная аппроксимация функции преобразования позволяет удовлетворительно решить поставленную задачу триангуляционных измерений для цели контроля формы поверхности детали приборного подшипника.

Итак, приведен вывод функции преобразования триангулятора на основе приближения геометрической оптики и гауссовых тонких пучков с использованием формул матричной оптики. Показано, что она имеет практически линейный вид во всем диапазоне оптических увеличений изображающего объектива, а также не зависит от размера апертуры. Это справедливо при малом относительном отверстии этого объектива, при котором пучок света, попадающий в него, является параксиальным. Проведена оценка составляющей погрешности метода, связанной с геометрией оптической схемы, без учета поперечной ширины пучка света, падающего на контролируемую поверхность. На конкретном примере показано, что в практически важной задаче она удовлетворяет требованиям технического задания.