Тригонометрическая система функций в проекционных оценках плотности вероятности нейросетевых признаков изображений

Большинство исследований в области распознавания изображений [1] сосредоточены на повышении точности, надёжности и вычислительной эффективности существующих решений за счёт применения новых архитектур глубоких свёрточных нейронных сетей (СНС) [2, 3, 4], новых классификаторов и их ансамблей [5, 6, 7], методов извлечения характерных признаков [8], алгоритмов приближённого поиска ближайшего соседа [9, 10] и пр. Несмотря на наличие большого числа хорошо зарекомендовавших себя подходов, основанных на технологиях глубокого обучения [1], интенсивность исследований в этом направлении не снижается. И связано это с тем, что современные методы распознавания характеризуются недостаточной точностью в вытекающих из потребностей прикладных исследований задачах, например, при наличии в базе данных малых выборок наблюдений (десятки эталонов для каждого класса) [11, 12], которые невозможно использовать для успешного обучения сложных нейросетевых структур [3, 4]. В таком случае наиболее часто используется перенос знаний или адаптация предметной области [7, 13], в котором глубокие СНС применяются не как метод классификации, а как способ извлечения признаков [8, 10]. Такая СНС предварительно обучается с помощью большого набора изображений, например, ImageNET [14].

В результате встаёт задача выбора наиболее подходящего метода классификации [15]. Достаточно перспективным здесь выглядит универсальный статистический подход [16, 17], в котором предполагается, что

Поэтому актуальной становится задача синтеза непараметрических статистических классификаторов, не требующих хранения и сопоставления всех признаков. Для её решения в настоящей работе показано, что если воспользоваться предположением о независимости главных компонент, выделенных из вектора признаков изображений [15], а для оценки плотности вероятности каждой компоненты вместо ядра Розенблатта – Парзена использовать проекционные оценки [21, 22, 23] на основе тригонометрических функций [24, 25], то возможно преодолеть отмеченные недостатки ВНС без потерь в скорости обучения. При этом получившаяся модификация ВНС будет также сходиться к оптимальному байесовскому решению. В ходе экспериментального исследования в задаче классификации категорий изображений и распознавания лиц для популярных баз данных Caltech-101 [26] и CASIA WebFaces [27] продемонстрировано повышение точности и вычислительной эффективности распознавания по сравнению с традиционными подходами в случае наличия ограниченного количества эталонов для каждого класса.

1. Задача распознавания изображений в условиях малого числа наблюдений на основе вероятностной нейронной сети

Задача распознавания состоит в том, чтобы поступающему на вход изображению одного объекта поставить в соответствие один из C > 1 классов [1, 12]. При этом для каждого c -го класса доступен набор из R ( c ) ≥ 1 эталонных изображений. Рассмотрим далее случай малых выборок [6, 12, 21]: R ≈ 1, который характерен для многих систем обработки изображений. Для каждого доступного изображения осуществляется извлечение характерных признаков. В наиболее часто используемых сейчас методах переноса знаний [2, 13] для настройки классификатора может использоваться не доступное обучающее множество, а внешняя база данных изображений, с помощью которой происходит обучение глубокой СНС [3, 4]. Далее для распознавания произвольных изображений они приводятся к одному размеру (высота U и ширина V ) и подаются на вход СНС [8, 10]. Выходы из D >>1 значений одного предпоследнего слоя нейронной сети нормируются (в метрике L ₂) и формируют вектор признаков x этого изображения с размерностью D . Аналогичная процедура применяется для извлечения D -мерного вектора признаков x r ( c ) из каждого r -го эталонного изображения с -го класса [12].

В итоге на этапе распознавания обучается классификатор выделенных признаков. В традиционном переносе знаний применяется логистическая регрессия – последний полносвязный слой исходной СНС заменяется на новый слой с C выходами (по одному на каждый класс исходной задачи), и происходит дообучение ( fine-tuning ) полученной нейросети для доступного обучающегося множества из R эталонов [2, 13].

В случаях малого числа наблюдений такая процедура оказывается недостаточно эффективной [11, 12], поэтому зачастую классификатор упрощается, например, с помощью снижения размерности векторов признаков [28] на основе анализа главных компонент [15], при котором векторы x и x _r ( c ) линейно преобразовываются в векторы M <<  D главных компонент t = [ t ₁, ..., t_M ] и t _r ( c ) = [ t_{r ,1}( c ), ..., t_{r , M} ( c )] соответственно. Далее могут применяться известные методы построения небольшого числа опорных подпространств [29] или отбора наиболее информативных эталонов [19, 30].

Проблема состоит в том [1, 17], что каждому конкретному образу обычно присуща известная вариативность, т.е. изменчивость его признаков от одного образца наблюдения к другому, которая носит случайный характер. Обычно преодоление данной проблемы связывают со статистическим подходом [15, 16], когда в роли образа выступает соответствующий закон распределения Pc векторов признаков объектов одного класса. В таком случае задача сводится к проверке C гипотез Wc о законе распределения P признаков входного изображения:

W c : P = P c , c = 1, C .                                (1)

Её оптимальное решение дает байесовский критерий минимума среднего риска [16] – делается вывод о принадлежности входного объекта к классу с максимальной апостериорной вероятностью

c * = argmax f ( t| W c ) • P ( W c ) .                      (2)

c e { 1,..._ C }

Здесь P ( W c ) – априорная вероятность появления c -го класса, f ( t | W c ) – условная плотность вероятности (оценка распределения P c ) главных компонент векторов признаков класса c . Для оценки априорной вероятности зачастую [18] используется соотношение числа эталонов в обучающих выборках P ( W c ) = R ( c )/ R , где R = Ъ C = 1 R ( c ) — общее число эталонов. Восстановление неизвестных законов распределения P c происходит в процессе предварительного обучения по выборкам { t r ( c )} конечных объёмов R ( c ). В предположении о нормальном распределении P _c могут применяться модификации линейного дискриминантного анализа [11]. С точки зрения современной прикладной статистики на практике обычно нет оснований полагать справедливость предположения о нормальном законе распределения для произвольных объектов [31, 32]. Поэтому большей популярностью в настоящее время пользуются непараметрические методы оценивания распределений [33], например [18]:

R ( c )

f (tlWc ) =      Ъ K (t, tr (c))

^R ( c ) r = 1

на основе гауссовского ядра Розенблатта–Парзена

K ( t , t r ( c ) ) =

• 1           f 1                      )

= ;-----TT M 72 exp I -      Ъ ( t m - t r ; m ⁽ c ) ) I -

(2ПС2 )        I 2° m=1

Здесь о - фиксированный параметр сглаживания. С учётом оценки (3) итоговое решение (2) может быть записано в виде

• ₁    R ( c )

c * = argmax — Ъ K ( t , t r ( c ) ) -                    (5)

c e { 1,..., C } R r = 1

Критерий (5) и представляет собой реализацию ВНС [18]. Здесь для каждого класса происходит сопоставление входного объекта со всеми признаками tr (c) каждого эталона. В таком случае алгоритмическая сложность реализации критерия (5) оценивается как O(RM). Сложность по затратам памяти O(RM) оказывается высокой из-за необходимости хранения всех эталонных объектов. В результате применение ВНС может быть неприемлемо для многих прикладных систем, функционирующих на малопроизводительном оборудовании [9].

Так как известного повышения вычислительной эффективности ВНС за счёт использования подходящих структур данных [34] оказывается обычно недостаточно, преодоление указанной проблемы связывают с выделением в обучающем множестве информативных эталонов [19, 30], которые и участвуют в дальнейшем распознавании. Наиболее популярный подход [19] сводится к предварительной кластеризации обучающего множества (чаще всего, на основе метода k-means [15]) и применении центроидов выделенных кластеров для обучения ВНС (3). К сожалению, такое решение приводит к потере основных достоинств ВНС. Действительно, процедура обучения становится достаточно сложной, а само решение перестаёт быть оптимальным в байесовском смысле, особенно для существенно различающихся по объёму кластеров [35].

и выполнить отсечение первых J членов тригонометрического ряда, то оценка плотности вероятности в (6) примет следующий вид [43]:

R ( c ) J 2

f c ( t m ) = — E EE Vk ) ( t m ' U ) ( t rm ( c )) .      (8)

R ( c ) t! j =0 и

К сожалению, реализация такого подхода оказывается в 2 J раз медленнее по сравнению с традиционной ВНС (5). Однако если выполнить несложные тригонометрические преобразования выражения (8), то можно получить эквивалентную оценку плотности вероятности с помощью ядра Дирихле [22, 40]:

VS f c ( t m ) =

1 2 R ( с )

R ( c )

E r=1

sin II J ⁺ 2 ) ⁽ t m - t r ; m ⁽ c ))

^2sin( t m - t r ; m ⁽ c ))

2. Проекционные оценки плотности вероятности в вероятностной нейронной сети

В настоящем праграфе оценки плотности вероятности [36, 37] с помощью гауссовских ядерных функций Розенблатта –Парзена [18] заменяются на известные проекционные оценки [38, 39], в которых плотность вероятности записывается как сумма ортогональных разложений [40, 41]. Ситуация резко осложняется для многомерного случая, в котором образуется многомерная ортонормированная система из всевозможных произведений одномерных базисных функций. В результате с ростом размерности M вектора признаков экспоненциально возрастает сложность вычисления ортонормированных функций [36] и, как следствие, требование к минимальному числу эталонов каждого класса, достаточных для оценки многомерного распределения. Поэтому использование такого подхода для классификации векторов значений признаков большой размерности на практике в общем случае не представляется возможным. В то же время стоит отметить, что для рассматриваемого случая – признаков главных компонент, выделенных из выходов глубокой СНС, – можно использовать предположение о независимости отдельных компонент векторов t и t r ( c ) [35]. Тогда плотность вероятности каждого класса запишется как

M f (t| Wc ) = П fe (tm ),                             (6)

m = 1

В результате асимптотическая сложность классификации (2), (6), (9) будет совпадать со сложностью ВНС. Именно в таком виде (с учетом различий в применяемой ядерной функции) традиционно записывается ВНС на основе проекционных оценок [36, 37], которая, хоть и приводит в ряде случаев к повышению точности, очевидно, не влияет на вычислительную эффективность классификации.

3. Предложенный подход на основе проекционных оценок плотности

Стоит отметить, что для тригонометрической системы функций не гарантируется неотрицательное значение выражения (9) [22, 43]. В связи с этим на практике обычно используются другие ортогональные функции, такие как многочлены Лагерра или Лежандра [22]. В нашей работе реализован альтернативный подход, в котором для оценки плотности вероятности f_c ( t_m ) вычисляется среднее арифметическое первых J частичных сумм тригонометрического ряда [43]. Эта оценка представима в виде (3), где вместо ядра Розенблатта – Парзена применяется ядро Фейера [40, 41]

1         1

f ( t ) =-- X

^Jc ( ^m ) R ( с )2( J + 1)

R ( c ) x E r = 1

( sin

J + 1

( t_m

t_{r ; m} ( c ))

sin

V

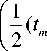
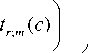
где одномерную плотность вероятности i -го признака f_c ( t_m ) можно оценить аналогично (3). Если вместо ядра Розенблатта – Парзена (4) воспользоваться проекционными оценками на основе ортогональной системы тригонометрических функций [24, 42]

^V T ( t ) = cos( n jt ), V(²⁾ ( t ) = sin( n jt )

Такой подход, хоть и приводит к неотрицательным значениям оценки плотности вероятности (6), не позволяет повысить вычислительную эффективность распознавания [20, 43]. Поэтому в настоящей работе предлагается воспользоваться другим, эквивалентным (10) выражением [35, 43]:

J 2

f c ( t m ) = 0,5 + EE a mj c ) 'V j ) ( t m ).            (11)

j = 1 k = 1

Здесь коэффициенты ряда предложено оценить по имеющейся обучающей выборке как среднее арифме-

тическое (J+1) обычных коэффициентов тригономет рического ряда (7), где m = 1, M, j = 0, J, k = 1,2:

( k ) m ; j

J - j ^{+ 1} R ( c ) • ( J + 1 )

R ( c )

E V j ⁾⁽ t_r ; m ⁽ C)).

r = 1

Тогда итоговое выражение для распознавания изображений (2), (6) при переходе к более удобному логарифму правдоподобия запишется в виде

M

J 2

Л max ce{1,..., C}

log R ( c ) + E log l 0,5 + EE a m^j (c ) V j ) ( t m ) I . (13)

m = 1

V

j = 1 k = 1

Таким образом, предлагаемый метод состоит в следующем. На этапе обучения для каждого класса вычисляются M (2J + 1) коэффициентов с помощью процедуры (12), имеющей линейную сложность. Далее в процессе распознавания изображение подаётся на вход СНС, выход предпоследнего слоя нормируется и преобразуется в последовательность из M главных компонент. После этого для каждой компоненты вычисляются J значений базисных функций (7). Для ускорения этой процедуры можно воспользоваться известными рекурсивными выражениями для тригонометрических функций суммы переменных:

• (1)             (1)            (1)            (2)           (2)

V j ( t ) = V j - i ( t ) ^V i ( t ) -V _{j - 1}( t ) ^V i ( t ),

• (2)             (1)            (2)            (2)           (1)

V j ( t ) = V j - 1 ( t ) ^V 1 ( t ) + V j - 1 ( t ) ^V 1 ( t )

с инициализацией v(1)(t) = cos(n t), v12)(t) = sin(n t). В итоге количество сложных операций вычисления тригонометрических функций сокращается в J раз (по сравнению с (7)).

Далее для каждого класса и каждой компоненты вектора t оценивается логарифм правдоподобия (13). Итоговое решение принимается в пользу максимально правдоподобного класса.

Остановимся подробнее на преимуществах предложенного подхода. Во-первых, сохраняются все основные преимущества традиционной ВНС: сходимость к байесовскому решению и чрезвычайно быстрая процедура обучения. Стоит отметить, что в предложенном подходе можно эффективно выполнить дообучение при появлении новых эталонных изображений. Действительно, при появлении нового эталона tR(c)+1(c) коэффициенты (12) могут быть скорректированы за константное время следующим образом amk j (c) =

R ( c ) • a mkj ( c ) + V j^k ) ( t_R ( c ) + 1; m ( c ))

R ( c ) + 1

Наконец, основным преимуществом предлагаемо- го подхода является низкая алгоритмическая сложность его реализации O(СMJ). Как известно [22, 38, 44], сходимость ряда (11) обеспечивается в том слу- чае, если параметр J определяется как o (VR(c)). В

результате вычислительная сложность предлагаемого алгоритма может быть оценена как

C

O\M E V R ( c ) I .

V     c = 1          7

В худшем случае, когда для каждого класса доступен только R ( c ) = 1 эталон, асимптотическая сложность реализации разработанной модификации и исходной ВНС одинаковы: O ( MR ). На практике в таком случае предложенный подход может оказаться в несколько раз медленнее за счёт суммирования в (13) 2 J +1 слагаемых. Наибольший выигрыш в скорости распознавания достигается для сбалансированных классов ( R ( c ) = R / C ). Тогда распознавание одного изображения в среднем оказывается приблизительно в R ( c )/ (2 3 J" R ( c )" | + 1) = ( R / C )^2/3/2 раз быстрее по сравнению с ВНС (3)–(5). Таким образом, предложенный алгоритм стоит применять вместо ВНС в случае R ( c ) / (2 3 " R ( c )" | + 1) >  1, то есть при наличии в обучающем множестве в среднем не менее R ( c ) =5 эталонных изображений. Кроме того, стоит отметить, что сложность по затратам памяти также снижается: O ( CD • ( RIC ) ^1/3)= O ( D • R ^1/3 C ^2/3) за счёт отказа от обработки всех элементов всех обучающих выборок ( memory-based approach ) и необходимости сохранения только коэффициентов (12).

Таким образом, разработанная модификация (12)– (15) позволяет преодолеть существующие недостатки (низкая вычислительная эффективность, отсутствие обобщения) оригинальной ВНС (4)–(5), сохранив при этом высокую скорость обучения и сходимость к оптимальному байесовскому решению. В следующем параграфе экспериментально продемонстрировано, что и для реальных задач распознавания изображений предложенный подход является не менее эффективным, чем традиционные классификаторы.

• 4. Результаты экспериментальных исследований

Эксперименты проводились на ноутбуке MacBook Pro 2015 (16 Гб ОЗУ, 4-ядерный процессор Intel Core i7 2,2 ГГц). В первом эксперименте рассмотрено применение предложенной модификации ВНС в задаче распознавания C = 101 категорий из набора Caltech-101, содержащего 8677 изображений [26]. Для извлечения признаков использовалась библиотека Caffe [46] и две глубоких СНС – Inception v1 (GoogLeNet) [3] и VGGNet с 19 слоями [4]. Нейросетевые модели, предварительно обученные для распознавания 1000 классов изображений ImageNet, были загружены с официального репозитория Caffe Model Zoo. На вход СНС подавались матрицы цветных (RGB) изображений из набора Caltech-101, приведённых к одной размерности U = V =224 пикселя. Выходы слоев «pool5/7×7-s1» (Inception v1) и «fc6» (VGGNet-19) нормировались в метрике L₂, после чего извлекались все главные компоненты для получения окончательных векторов признаков размерности M = 1024 и M = 4096 для Inception и VGGNet-19 соответственно.

В течение 10 раз повторялся следующий эксперимент. В обучающее множество из каждого класса наугад выбиралось фиксированное число изображений R ( c ), а тестирование проводилось на всех остальных изображениях. Для проверки значимости различий в точности и времени распознавания применялся критерий Мак-Немара с уровнем значимости 0,05. Оценки точности классификации α (%) и среднего времени распознавания одного изображения t (мс) для 10 и 25 эталонных изображений в каждом классе R ( c ) представлены в табл. 1 и табл. 2 для признаков, извлечённых с помощью Inception и VGGNet-19 соответственно.

Табл. 1. Результаты распознавания изображений для набора фотографий Caltech-101, Inception v1

Здесь извлечение признаков с помощью VGGNet-19 привело к меньшей точности распознавания по сравнению с GoogLeNet для малого числа эталонных изображений каждого класса (R(c) = 10), но при повышении числа эталонов для ряда методов классификации признаки VGGNet оказались более точными. Подтвердился известный факт о недостаточной эффективности сложных классификаторов (SVM, random forest, искусственная нейронная сеть) при небольших объемах обучающих выборок.

Табл. 2. Результаты распознавания изображений для набора фотографий Caltech-101, VGGNet-19

В следующем эксперименте рассмотрена задача идентификации лиц [1, 12]. Использовались 66000 фотографий первых C = 1000 людей из базы данных фотографий лиц CASIA WebFaces [27]. Для извлечения признаков применялась наиболее точная из свободно доступных нейросетевых моделей – Light СНС (версия C) [47], обученная её авторами с помощью сверхбольшого набора фотографий лиц MS-Celeb-1M. Эта СНС извлекает D = 256 вещественных признаков из полутонового изображения лица с высотой

U = 128 и шириной V = 128 пикселей. Результаты эксперимента приведены в табл. 3.

Табл. 3. Результаты распознавания лиц для набора фотографий CASIA WebFaces, Light СНС

В то же время предложенная модификация (12)– (15) во всех случаях является более предпочтительной как по вычислительной эффективности (в 2,7– 6 раз), так и по точности (на 2–4%), чем оригинальная ВНС (4)–(5). При этом с точки зрения критерия Мак-Немара повышение эффективности по сравнению с ВНС оказывается статистически значимым. Стоит отметить, что в связи с большим числом классов разработанный подход даже для R ( c ) =30 эталонов оказывается более точным по сравнению с остальными методами классификации.

Заключение

Таким образом, в настоящей работе предложена модификация ВНС (12)–(15), основанная на проекционных оценках плотности вероятности, которые используют систему тригонометрических функций и предположение о независимости признаков классифицируемого объекта. Показано, что разработанная модификация сохраняет основные преимущества оригинальной ВНС: сходимость к байесовскому решению, линейное время обучения и константная сложность дообучения. При этом предложенный подход является намного более эффективным с точки зрения вычислительной сложности и затрат памяти (выигрыш до ( R / C )^2/3/2 раз) за счёт отказа от хранения признаков всех эталонов и обучения модели с помощью вычисления коэффициентов (12) усреднённого тригонометрического ряда (11). Результаты экспериментального исследования для признаков, извлечённых с помощью современных СНС Incep-tion,VGGNet и Light СНС, показали, что разработанная модификация не только во всех случаях оказывается предпочтительнее исходной ВНС, но и является наиболее точным классификатором для малого числа эталонных изображений.

Основным недостатком предложенного подхода по сравнению с классической ВНС является отсутствие в нём аналога выражения (4), в котором вычисляется расстояние между векторами признаков входного и эталонного изображения. В результате для нашей модификации оказывается недоступным повышение точности ВНС за счёт применения в (4) мер близости более сложных, чем метрика Евклида [5]. Кроме того, стоит отметить, что реализация предложенного подхода оказалась медленнее оригинальной ВНС при наличии очень малого (менее 5) числа эталонов для каждого класса в связи с оценкой отдельной плотности вероятности для каждого признака при вычислении выражения (6).

В то же время следует отметить необходимость проведения ряда дополнительных исследований. Прежде всего, следует оценить точность распознавания изображений для оценки плотности вероятности с помощью других известных ортогональных систем (например, многочленов Лагерра или Лежандра) [22, 23]. Также стоит проанализировать возможность адаптации разработанного метода к обработке больших данных, например, на основе последовательного анализа [48, 49] иерархического представления изображений [2] с применением предложенного подхода для предварительной отбраковки большинства классов и выбора окончательного решения с помощью одного из традиционны классификаторов. Наконец, представляет интерес исследование применимости предложенного подхода для признаков, выделенных СНС с небольшим числом параметров, таких как Mo-bileNet, SqueezeNet, в расчёте на их реализацию на мобильных устройствах.

Исследование выполнено при поддержке гранта президента РФ для молодых ученых – докторов наук № МД-306.2017 и Лаборатории алгоритмов и технологий анализа сетевых структур (ЛАТАС) Национального исследовательского университета Высшая школа экономики. Работа параграфов 3 и 4 выполнена за счёт гранта Российского научного фонда (проект № 14-41-00039).