Трисекция угла с линейкой и циркулем, не используя невсиса. N-секция любого угла

(Всё указанное во "Введении" использовано в Трисекция угла — Википедия .)

"Невсис позволяет достаточно просто решить задачу трисекции произвольного угла.

Рис. 1. Трисекция угла с помощью невсиса

Рис. 2. Трисекция угла (доказательство)

Доказательство

Рассмотрим треугольник ABO (рис. 2). Так как AB = BO = a, то треугольник равнобедренный, и углы при его основании равны: LBAO = ^BOA = в- Угол L PBO как внешний угол треугольника ABO равен 2в.

Треугольник BPO также равнобедренный, углы при его основании равны 2в, а угол при вершине у = 180°-4в- С другой стороны, у = 180°-в-а. Следовательно, 180°-4р = 180°-в-а и а = 3р.

Задача трисекции угла решена именно в России Николаем Степановичем Поповым, к.т.н.? См. "Юный техник", №12, 1994г, с. 62-64."

Я попытаюсь принять развитие в Википедии и буду описывать Доказательства, использовать, в том числе, комплексную переменную.

Трисекция угла с линейкой и циркулем.

Сначала строится случайный острый угол с точкой в острие угла, нижняя сторона выбирается горизонтальной.(см. рис. 3)

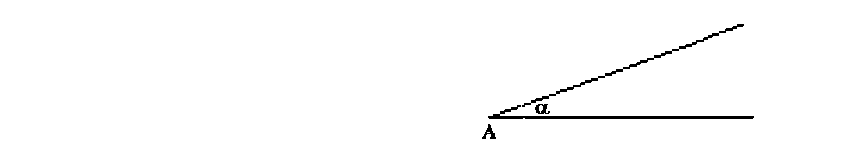
рис. 3

Продолжается нижняя сторона угла А. (см. рис. 4)

рис. 4

Выбирается случайный (не слишком большим или малым) раствор циркуля. Острие циркуля ставится в точку A на горизонтальной линии и производятся справа и слева от этой точки засечки циркуля с точками B и C. После этого, острие циркуля ставится в точку C на горизонтальной линии и производятся слева от этой точки засечки циркуля с точкой D. (см. рис. 5)

рис. 5

Теперь острие циркуля ставится в точку D на горизонтальной линии и устанавливается раствор циркуля до точки B (т.е. раствор циркуля увеличивается ровно в три раза). После этого, производится засечка на верхней линии угла. (см. рис. 6)

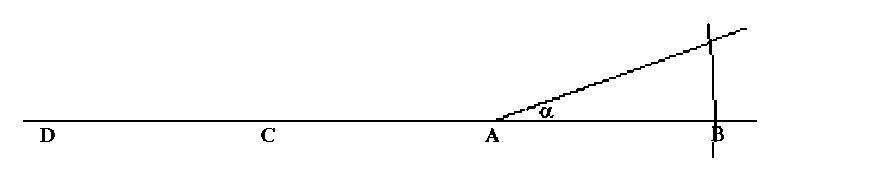
рис. 6

Отмечаем в этой засечки точку E. С помощью линейки соединяем точки D и E. (рис. 7)

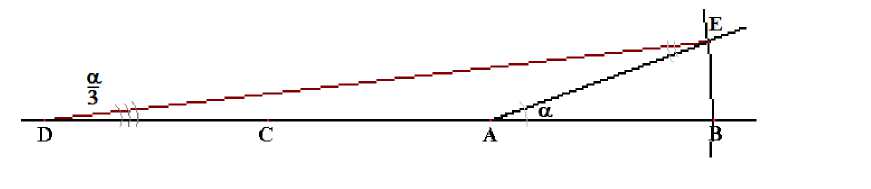
рис. 7

Таким образом, получившийся угол ∟ BDE будет ровно в три раза меньше, чем ∟ BAE. Кроме того, соотношение AB к DB есть 1:3

Доказательство.

На рис.2 проведём циркулем окружность из точки A через точку P.

(см. рис. 8, дополненный рис.2).

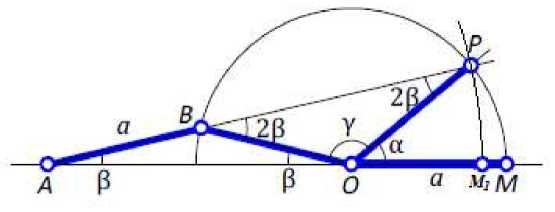
рис. 8

Рассмотрим как отличаются рис.2 и рис.7. Поскольку длина отрезка

OM рис.8 отличается от отрезка AB рис.7 (составляющий отрезок OM 1

рис.8). Из рис.7 видно, что длина отрезка AB в точности составляет половину отрезка AD. Следовательно, необходимо определить соотношение отрезков AO и OM₁ из рис.8. Т.е. либо отношение AO к OM₁ состоит 2 к 1, либо отношение AP к OM 1 состоит 3 к 1, либо отношение AP к AO состоит 3 к 2.

Тот факт, что задача о трисекции угла в общем случае неразрешима в принципе, был доказан в 1837 году. И это доказательство признано всем математическим миром. Однако, всё это относится лишь к тригонометрии. Но, ведь, справедливость трисекции произвольного угла использования невсиса не даёт нам покоя! Попробуем использовать комплексные значения.

Показательная форма записи комплексного числа имеет вид:

i ф z=re ⁹

Горизонтальная линия будет действительная ось координат, а вертикальная - мнимая. Кроме того, можем для одинаковых длин отрезков можем выбирать размеры отрезков равные единице. В этом виде комплексные значения будут иметь вид z=e i ⁹ .

Используем получение отрезка AD сумму трёх комплексных значений: AD =e i ⁹ + e -i ⁹ + e i3 ⁹ . Не действительной оси мы получаем AC =e i ⁹ + e -i ⁹ . (см. рис. 9)

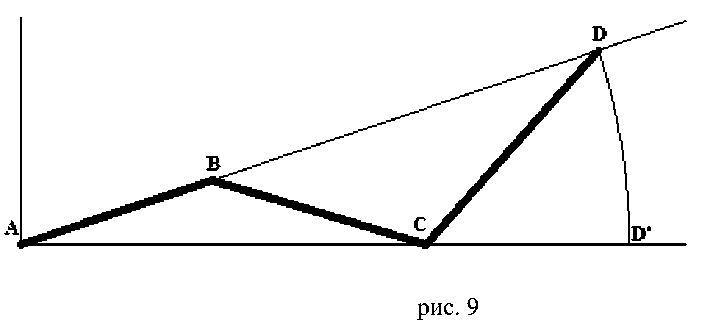
Кроме того, используем получение отрезка AD сумму трёх комплексных значений: AD =1 + e i2 ⁹ + e^-i 2 ⁹ . Не действительной оси получается весь AD . (см. рис. 10)

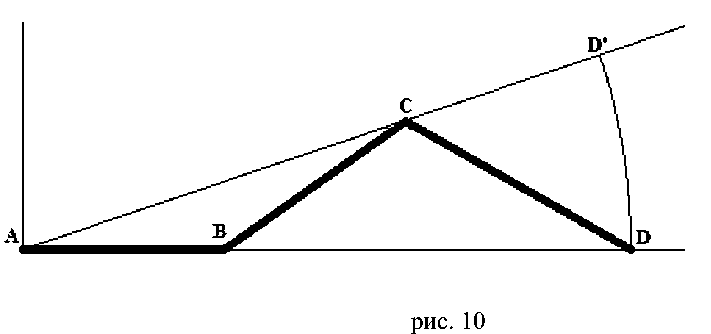
Теперь, перепишем значения отрезков AC из рис.9 и AD из рис.10.

Используя дествительные значения отрезков, можно написать:

AD =1 + e i ^{2 9} + e^{-i2 9} = 1 + e i ^{2 9} + e i ^{2 9} = 1 + 2e i2 ⁹ , и

AC =e i ⁹ + e -i ⁹ = e i ⁹ + e i ⁹ = 2e i ⁹ .

Тогда так выглядет определение соотношений:

AD     1 + 2e i2 ⁹      1

AC

2e i ⁹

e -i ⁹ + e i ⁹ = -у e i ⁹ + e i ⁹ = -3 e i ⁹

Здесь мы игнорируем знаком степени e i ⁹ и e -i ⁹ , т.к это не имеет значение действительной части. Теперь, рассмотрим соотношения AD (из рис.10) к разнице ( AD - AC ) (из рис.9). имеем вид:

i2 9

---—---= —=---     \----v— =e-i39+2e-i9 = e-i29( e-i9 + 2ei9)= 3ei9

AD - AC      e i ⁹ + e -i ⁹ + eⁱ³⁹ - 2e i ^{9    e          e (e} + 2 ^e ) ^3e

Теперь, соотношения (из рис.9), пожно показать:

AC ₌   3 / 2e i ⁹

CD'       3e i ⁹

N-секция любого угла.

Если любой угол даже тупой, его можно поделить пополам столько раз, пока он не станет острым. После этого с циркулем и линейкой получить трисекцию угла, а полученный можно ровно на столько же раз удваивать.

Для того же, что любой угол делить можно на любое число K, нужно извлечь корень числа K из комплексного числа z=re i ’ , т.е:

Nz= k^rei’/k.

Таким образом, получившийся угол будет ровно в K раз меньше, чем ф . Кроме того, соотношение нижней стороны исходного угла к нижней стороне полученного угла будет 1:k .

DIXI

"Экономика и социум" №6(37) 2017