Трёхмерная численная модель для химически активного тлеющего разряда в воздухе

В работе рассматривается численное моделирование тлеющего разряда постоянного тока в воздухе между двумя плоскопараллельными электродами (рис. 1). Используемая программа является результатом последовательного развития численных моделей, описанных в работах [1–3]. Данная численная модель, построенная на основе диффузионно-дрейфовой модели разряда, позволяет рассчитать параметры тлеющего разряда, согласующиеся с имеющимися экспериментальными данными. В том числе концентрации электронов и ионов как в положительном столбе, так и в приэлектродных областях, распределение напряжённости электрического поля, проводимость газа, плотности тока на электродах, полный ток через разряд и внешнюю цепь. В данной численной модели также добавлен расчёт многокомпонентной диффузии и колебательной кинетики в молекулярных азоте (N 2 ), кислороде (O 2 ) и окиси азота (NO) в тлеющем разряде. Это позволяет предсказать распределение указанных молекул по колебательным уровням, что представляет интерес для использования в различных аэрокосмических приложениях и лазерной физике.

Модель процесса включает в себя трёхмерные уравнения неразрывности элек-

тронной и ионной концентраций, уравнение Пуассона для электростатического поля, уравнение теплопроводности, а также уравнения химической кинетики для колебательно возбуждённых молекул:

∂ne ∂t

+ div Гe = а(IE|) |Ге| - pnine

di + div Гi = а(IE|) |Гe| - enine

A v +--( n i — n e ) = 0

s 0

8T , _____ „

pcp — = div( X^T) + Q

PdYk + div Jk = Wk, ∂t

к = 0 ...m

Wk =

M fc KS П njs — E K П j s           js               s           js

Ms E

ρ

' j = k

Y j J _k - Y _k J j M k M j D kj

VM s Y k

M k

j

к = 1 ...m

_ 3 V R ¹ T ( M k + M j ) / ( M k M j )

Djk   8 Vn     na2 j fi(1,1) (T/ejk)

С краевыми условиями:

г = 0 :

^dn i = 0 , Г e = y Г i , V = 0;   J k,z = 0

∂z г = Hc :

∂n n = 0, — = 0, ^ = V; Jk,z = 0 ∂z

• x = 0 , x = d _e :

∂ne   ∂ni

Tj— = Tj— = 7T- = 0; Jk,x = 0 ∂x   ∂x∂x

• y = 0 , y = d e :

• 9_ne = 9n, = Эф = 0. J, =0 ∂y ∂y ∂y

Здесь H e x d e x d e — размеры расчётной области, n _e , n i , Г _e , Г i — концентрации и потоки заряженных частиц, а ( E ) — первый коэффициент Таунсенда, β — константа рекомбинации, ϕ — потенциал, T — температура нейтралов, Y k , J k , — массовые доли и потоки нейтральных компонентов, D jk — коэффициенты бинарной диффузии, M k , M ^Σ — молярные веса компонентов и смеси, K _j ^± — константы скорости колебательных и вторичных реакций.

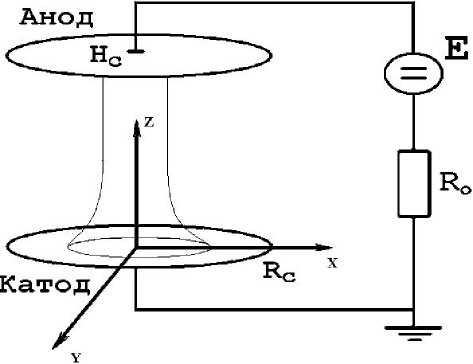
Рис. 1. Схема тлеющего разряда

Учёт электронной температуры производился с помощью эмпирической зависимости, получающейся аппроксимацией экспериментальных данных Таунсенда и Бай-ли [4]: Te/T = 14,5 ln (\E| /p) + 16,0. Колебательная кинетика моделировалась в рамках поуровневого описания с учётом процессов колебательного возбуждения молекул электронным ударом, колебательного обмена и колебательно-поступательной релаксации. Учитывались 30 колебательных уровней азота и по 2 уровня кислорода и окиси азота. Заселённость колебательных уровней определяется балансом процессов возбуждения колебаний электронным ударом (эВ), перераспределением колебательной энергии между уровнями (VV обмен) и процессами релаксации. В модели учтена только преобладающая VT релаксация. Кинетическая схема аналогична описанной в [2, 3].

Решение указанной системы уравнений представляет значительные вычислительные трудности [1], связанные с жёсткостью уравнений дрейфово-диффузионной модели, химической кинетики, а также с большим числом химических компонентов и большой размерностью задачи. При этих условиях особое значение имеет вычислительная эффективность алгоритма. В данной работе для решения использована полуявная вычислительная схема, сочетающая вычислительную экономичность с достаточно быстрой сходимостью. Учитывая наличие выделенного направления вдоль оси Z , естественно решать уравнения неразрывности вдоль оси Z более точно, чем в радиальном направлении. Соответствующий алгоритм основан на комбинации прогонки в продольном (ось Z ) и релаксации в поперечных (оси X и Y ) направлениях. Подстановкой уравнения Пуассона в уравнения неразрывности заряженных частиц и использованием эмпирической зависимости 5E/E ~ —5n _e /n _e удалось ослабить зависимость потоков зарядов и частоты ионизации от напряжённости электрического поля. В результате уравнения неразрывности электронов и ионов приводятся к виду, удобному для численного решения. Аналогичный вид принимают уравнения теплопроводности и Пуассона. Уравнения неразрывности нейтральных компонентов приводятся к виду, удобному для итерационного решения, следуя методике, описанной в [5]:

( - Лz De Лz + ae De Лx + ae De Д J ^e + hx         hy

+--^e [(2ne — ni) Ce — neCi] +

ε 0

+ (EЛ) ЦсСС + EbE- -    ^ £,c +

+eniCe + eneCi = fe — ^enef^,

fe = (ЛDeЛ) ne— (Л^eneЛ^) + Uionne—enine,

αα

• ^{— Л} z D i ^Л z + T~Di ^Л x ⁺ TTDi ^Л У ) h _x          h _y

  ^C i +

  
  

  + e^ i [(2 n i

  ε 0

  
  

  ^- n e ) C i ^- n i C e ^] -

  
  

  - ⁽ E Л) ^ i C i + ^ E dEE n - ^ ion^ C e +

  
  

  + en i C e + вП е С 1 = f i + № f p

  
  

  f i = (Л D i Л) n i + (Л ^ i n i Л v) + U ion H e -en i n e ,

  
  

  (Л z Л z - O p Л x - 0 ^ Л y) C p + e ( C i -C e ) = f p , h _x        h y           ε 0

  f p = ^- (^ЛЛ) V     ⁽ n i ^- n e ) ,

  ε 0

  
  

  ^a c ^ k ^C k ^-

  
  

  ^aa cz ^Л z B k ^Л z ^-

  
  

  ^{- a} cxy B k

  
  

  ( A x + Л к h x h y

  
  

  C k =

  
  

  a _T = 0 , 55-2 , 5. Сходимость контролировалась по изменениям счётных полей ( ϕ,n _e ,n _i ,T,Y _k ) на глобальной итерации. Найдено, что устойчивость алгоритма и его скорость сходимости сильно зависят от значений коэффициентов релаксации. При оптимальных значениях этих параметров ^{( a} p ⁰ , ^{53, a} e ^a i ² , ², ^a C ² , ⁰, a _Cxy = 1 , 5, a _Cz = 3 , 5, a _T = 0 , 55) стационарное решение получалось за (0 , 5-3) х 10 3 итераций, что на 1–2 порядка величины меньше необходимого числа итераций по методу [1, 2].

  Численное моделирование показывает узкую прикатодную область пространственного заряда (около 0 , 1 см). Разряд горит в режиме «нормальной плотности тока», когда катодное пятно занимает только часть площади электрода.

  
  
  
  

  _-

  
  

  ^Л x J k.

  
  

  ^{- Л} y J k,y ^{- Л} z J k,z + W k ,

  
  

  (Л z А Л z - xO T Л x - xO T Л y^ C t =

  
  

  = ^- ^Xv^А Л) T ^- n ^{( j}E ) .

  Здесь ξ e , ξ i , ξ k , ξ ϕ , ξ T — приращения концентраций электронов, ионов и k -го нейтрального компонента, потенциала и температуры соответственно, Л — оператор конечной разности, α e , α i , α ϕ , α c , α cxy , α cz и α T — релаксационные коэффициенты. Преобладание дрейфовых членов над диффузионными в уравнениях неразрывности заряженных компонентов приводит к необходимости использования направленных разностей при аппроксимации конвективных слагаемых [1], поэтому алгоритм имеет первый порядок пространственной аппроксимации. Уравнения неразрывности электронов и ионов решались совместно векторной прогонкой, а все остальные уравнения — независимо, скалярной прогонкой.

  Вычисления проводились для воздуха (79%N 2 , 21%O ₂ ) при давлении p = 5 Торр на сетке 100 х 100 х 200 узлов. Использовалась прямоугольная сетка, равномерная вдоль направлений X и Y . Вдоль направления Z сетка имела вдвое большее число узлов и сгущения в приэлектродных областях. Алгоритм тестировался при различных значениях релаксационных параметров: а _р = 0 , 52-1 , 0, a _e = a i = 1 , 0-3 , 0, a c >  1 , 0, a cxy = 1 , 0-3 , 0, a cz = 1 , 5-5 , 0,

  
  
  

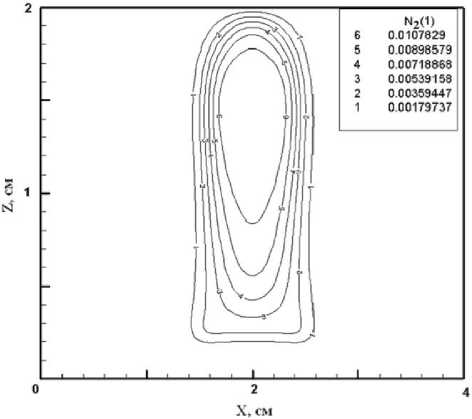
  Рис. 2. Массовая доля N ₂ ( v = 1)

  
  
  

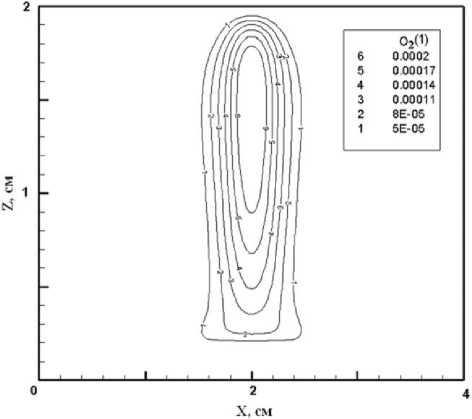
  Рис. 3. Массовая доля O ₂ ( v = 1)

  
  

Вычисленные поля массовых долей N 2 , O 2 в плоскости XOZ в колебательном состоянии v = 1 представлены на рис. 2, 3. На рис. 2 видно, что наибольшая доля колебательно-возбуждённых молекул N ₂ и O 2 достигается в центральной области разряда, где высока концентрация электронов. Основная часть колебательно-возбуждённых молекул занимает нижние уровни, с ростом номера уровня его заселённость падает.

Модель может быть использована для исследования различных процессов в тлеющем разряде, что представляет практический интерес для аэрокосмических приложений.

Работа выполнена в рамках программы фундаментальных исследований ОЭММПУ РАН (координатор академик Д.М. Климов) и программы фундаментальных исследований ОЭММПУ РАН (координатор академик Г.Г. Чёрный).