Трёхмерный расчёт фокусировки лазерного излучения коническим диэлектрическим зондом

Простейший конический диэлектрический зонд представляет собой кусок оптического волокна, конически вытянутого с одной стороны [1].

Заметим, что угол при вершине таких конусов значительно меньше угла полного внутреннего отражения [2, 3], и, в отличие от рефракционных аксико-нов [4, 5], эти конусы не предназначены для формирования бездифракционных световых пучков с протяжённой глубиной фокуса [6, 7].

Конические зонды с малыми углами при вершине широко используются в оптике ближнего поля [1, 8– 13]. Как правило, такие зонды покрыты тонким слоем металла и могут иметь или не иметь апертурное окно – зависит от способа применения такого зонда. Разрешение ближнепольного микроскопа в этом случае зависит, соответственно, от размера апертуры или кончика зонда, которые имеют наномасштабные характеристики. Такие структуры можно использовать для острой фокусировки [9, 11, 12], но энергетическая эффективность будет очень малой [14].

Для таких приложений, как субволновое микроструктурирование поверхностей, желательно увеличить долю пропускаемой энергии, не слишком ухудшая разрешение. В этом случае используют диэлектрические тейперы без покрытия с очень маленьким углом [15, 16]. Аналогичные устройства применяют для захвата и перемещения микрочастиц [17].

В работе [18] в рамках геометрооптического анализа было показано, что аксиконы с малыми углами могут как фокусировать, так и создавать расходящееся излучение. Формирование действительного и мнимого фокусов периодически меняется при уменьшении угла при вершине. Причем для меньших углов эта смена происходит быстрее. Изменение угла на доли градусов приводит к существенному изменению картины. В этой же работе было выполнено двумерное моделирование с использованием метода конеч- ных элементов, подтвердившее теоретические результаты.

Хотя двумерная модель иногда используется для расчётов распространения излучения в тейперах [19], более корректно выполнять трёхмерное моделирование [20], особенно при необходимости учёта поляризационных эффектов [21–24].

В данной работе с использованием метода конечных элементов (FEM) решения уравнения Гельмгольца выполнен расчёт фокусировки TE-поляризованно-го Гауссова пучка с помощью диэлектрических микроконусов с углом при вершине от 8 до 27 градусов.

Численное моделирование

В работе [18] рассмотрена дифракция Гауссовых пучков на рефракционном аксиконе в случае, когда угол аксикона значительно меньше предельного, соответствующего полному внутреннему отражению. Данная особенность интересна тем, что обычно считается, что при малом угле раскрыва аксикон не пропускает падающее излучение. Однако в [18] было показано, что при малых углах раскрыва в аксиконе происходит несколько полных внутренних отражений и аксикон может являться как фокусирующим, так и рассеивающим и коллимирующим. Получены следующие формулы.

Фокусировка будет наблюдаться в узких диапазонах углов раскрыва аксикона а 0 , определяемых неравенствами:

«1 -а <а r,(1)

где а ex находится из равенства:

n cos [(2p + 1)аmax ] = cos (a^),(1а)

а a m e al определяется из выражения:

n cos [(2 p + 1)а ^] = 1.(1б)

Выражения (1a), (1б) дают границы при p -кратном внутреннем отражении, p ≤1.

Расфокусировка при p -кратном внутреннем отражении будет наблюдаться в более широких диапазонах углов, определяемых неравенствами:

app             app amin < a0 < amax , где ncos[(2p- 1)aamp] = 1,p > 2,(2a)

n cos [(2p + 1)amp ] = cos (amp), p > 1.(26)

Ход лучей, рассмотренный в [18], приведён на рис. 1.

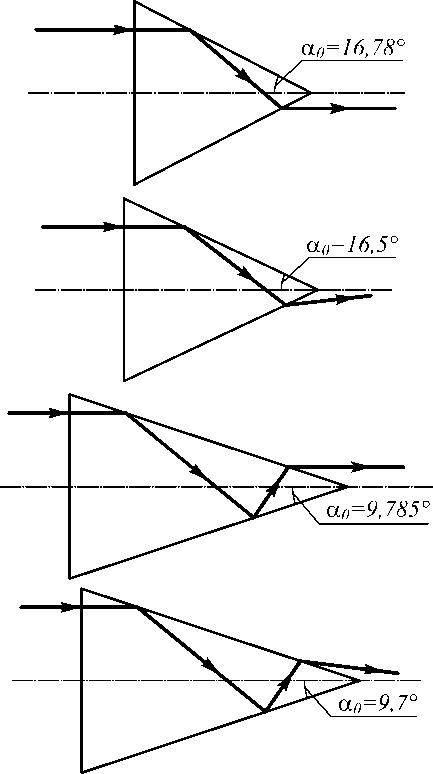
Рис. 1. Ход лучей при а , = 16,78 ; 16,5 ; 9,785 ; 9,7 ° (взято из [18])

Однако необходимо отметить, что геометрооптический подход, примененный в [18], не учитывает поляризации, коэффициентов Френеля, волновой природы света. Другой подход в [18], основанный на решении стационарных уравнений Максвелла, был применен только для двумерного цилиндрического случая. То есть фактически рассматривалась дифракция на клине бесконечной длины, а не на аксиконе. В настоящей статье рассмотрена дифракция на трёхмерном аксиконе. Общий вид схемы моделирования приведён на рис. 2.

Исходя из формул (1) и (2), а также расчётов статьи [18] в волновом случае, можно утверждать, что трёхмерный аксикон может быть рассеивающим, коллимирующим и фокусирующим при разных углах раскрыва.

В работе проведён расчёт дифракции Гауссова пучка на трёхмерном аксиконе при вариации угла раскрыва α0 от 8 до 27 градусов. Картины дифракции представлены в табл. 1. Длина волны выбрана равной λ = 532 нм. Высота аксикона равна 7λ, радиус основания варьируется от 0,984λ до 3,567λ и определяется углом раскрыва аксикона. На рис. 3 приведено два гра- фика зависимости амплитуды электрического поля на оптической оси после аксикона в двумерном случае (взято из [18]) и в трёхмерном случае (рассчитано в настоящей работе) от угла раскрыва аксикона α0.

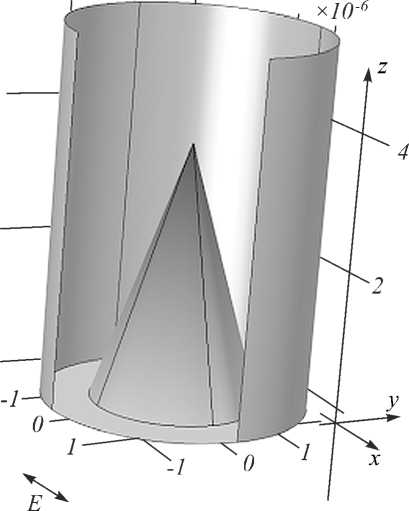
Рис. 2. Общий вид трёхмерной расчётной области: стеклянный аксикон (показатель преломления n = 1,5), размещенный в вакууме (показатель преломления n = 1)

Можно видеть, что при дифракции Гауссова пучка на трёхмерном аксиконе и двумерном клине данные элементы ведут себя сходным образом в смысле возникновения максимумов и минимумов интенсивности на оси. Но при одинаковых значениях угла раскрыва у двумерного и трёхмерного аксикона могут наблюдаться противоположные действия: так, при α0 = 14 º у клина наблюдается минимум интенсивности, а у ак-сикона – максимум.

Анализ поведения графиков на рис. 3 позволяет сделать вывод о том, что у трёхмерного аксикона период перехода от фокусировки к расфокусировке примерно в два раза больше, чем у двумерного.

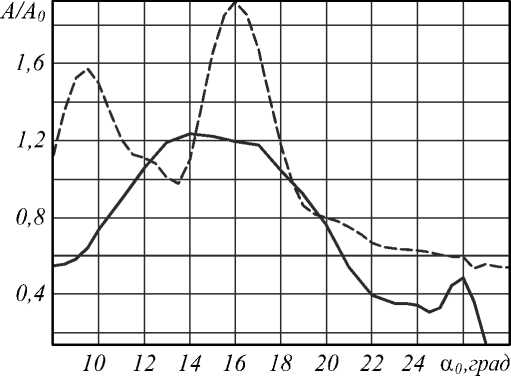
Рис. 3. Графики зависимости амплитуды электрического поля на оптической оси после аксикона от угла раскрыва аксикона а ₀ в двумерном случае (пунктирная линия) и в трёхмерном случае на расстоянии 1,65 длин волн (сплошная линия) от острия аксикона

На рис. 4 показаны картины дифракции на трёхмерном аксиконе (рис. 4а, в) и двумерном клине (рис. 4б, г) в сечении ZOY при двух углах раскрыва: α0 = 14 º (рис. 4а, б), α0 = 24,5 º (рис. 4в, г)). Размер приведённых картин на рис. 4а составляет 10λ × 7,2λ, на рис. 4в – 10λ ×8λ, на рис. 4б – 20λ × 10λ, 4г – 20λ × 11λ. Освещающий Гауссов пучок имел X-поляризацию.

Из рис. 4 следует, что трёхмерный аксикон может быть как рассеивающим (при α 0 = 24,5 º), так и фокусирующим (при α 0 = 14 º). Следовательно, выводы, полученные для двумерного случая на основе геометрооптического и волнового подходов, вполне экстраполируются и на трёхмерную модель.

Для наглядности покажем на рис. 5 распределения амплитуды электрического поля в поперечном сечении на расстоянии 1,65 длины волны от острия акси-кона для углов α 0 = 14º, α 0 =24,5º.

Из рис. 5 видно, что при прохождении излучения через аксикон с углом раскрыва α 0 = 14º основная энергия сконцентрирована у оптической оси, а при α 0 =24,5º – основная энергия рассредоточивается по периферии.

Табл. 1. Распределения амплитуды электрического поля для диапазона углов аксикона а 0 е [8 ° 27 ], показатель преломления аксиконов n = 1,5, длина волны излучения λ = 532 нм, высота аксиконов – 7 длин волн

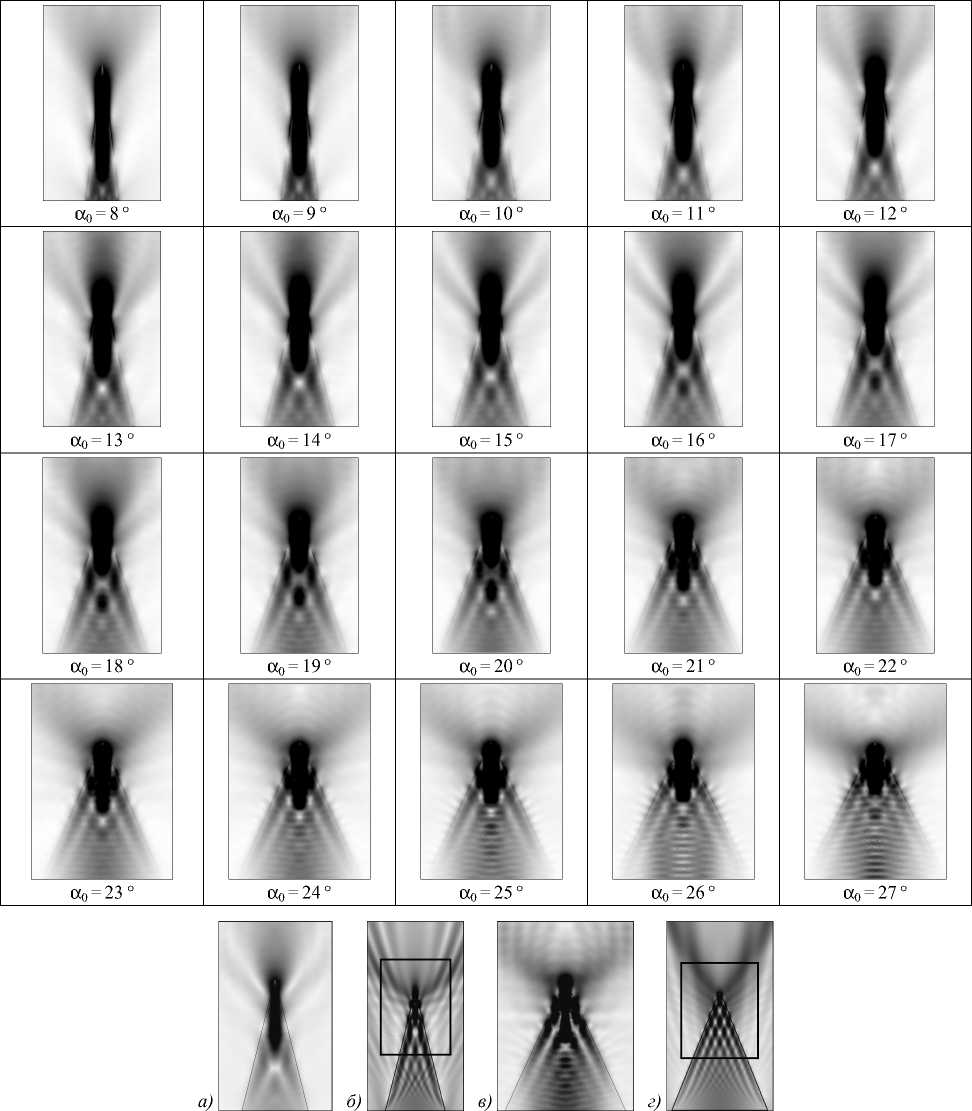
Рис. 4. Картина дифракции Гауссова пучка на трёхмерном аксиконе (а, в) и на двумерном клине (б, г) в сечении ZOY при угле раскрыва α0 = 14 º (а, б) и α0 = 24,5 º (в, г).

Размер приведённых картин составляет 10λ × 7,2λ (а), 10λ × 8λ (в), 20λ × 10λ (б), 20λ × 11λ (г)

• • с

• а)                            б)

Рис. 5. Распределение амплитуды электрического поля в поперечном сечении на расстоянии 1,65 длины волны от острия аксикона при освещении основания Гауссовым пучком при угле раскрыва α0 = 14 º (а) и α0 = 24,5 º (б). Радиус расчётной области составляет 4λ

Заключение

Рассмотрено действие конического диэлектрического зонда в трехмерной модели при прохождении через него Гауссова пучка. Рассчитаны картины дифракции при вариации угла раскрыва конуса от 8 до 27 градусов.

Показано, что трёхмерный зонд с углом раскрыва α0 = 14º является фокусирующим, а при α0 = 24,5 º – рассеивающим. Однако необходимо отметить, что в двумерном случае аксикон с углом раскрыва α0 = 14º является рассеивающим.

Анализ дифракции Гауссова пучка на диэлектрическом тейпере в двумерном и трёхмерном случаях позволяет сделать вывод о том, что у трёхмерного аксикона период перехода от фокусировки к рассеянию излучения примерно в два раза больше, чем у двумерного.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, а также грантов РФФИ 16-37-00241, 16-07-00825.