Троичная запоминающая ячейка и троичные триггеры

В последнее время интерес к троичной логике и арифметике возрождается во многом благодаря новым возможностям полупроводниковой технологии. В мире широко проводятся теоретические исследования, затрагивающие так или иначе трёхуровневую технику. Ежегодно проводится всемирный симпозиум «International Symposium on Multiple–Valued Logic» [1], на котором докладываются новейшие разработки в области многозначной логики. В литературе представлено множество статей и ряд монографий, предлагающих различные подходы к решению задачи построения устойчивого троичного элемента [2--6]. Обзор российских и зарубежных патентных документов показал непрерывность, а также актуальность развития троичных технологий. Преимущества троичной логики в ЭВМ по сравнению с двоичной: высокая вирусоустойчивость компьютерных программ, так как в троичной логике ЭВМ легче выделить вредоносные программы как инородные и самостоятельно принять решение об их изоляции или уничтожении; коды троичной логики короче и соответственно ЭВМ может в несколько раз быстрее производить сложные математические вычисления, чем ЭВМ с двоичной логикой; в случае каких-либо сбоев в отдельных программах ЭВМ не будет зависать, как это часто происходит в двоичной системе исчисления и его не нужно будет перезагружать заново, теряя при этом полезную информацию. Здесь просто можно будет выходить из программы, давшей сбой, и продолжать работать в других программах; троичная (пятеричная и т.д.) система исчисления позволяет создавать кибернетические устройства (в том числе и соответствующие программы) с элементами искусственного интеллекта, что в свою очередь существенно упростит пользование такой ЭВМ.

Настоящая статья посвящена актуальной проблеме построения триггерных схем на основе логических элементов троичной логики. Вопрос построения элементов хранения является центральным в схемотехнике цифровых устройств, по- скольку элементы памяти являются основой построения всех последовательностных схем.

В публикациях отсутствует информация по логической организации трёхстабильных элементов хранения. А различные решения по построению схем троичных триггеров, приводимые в российских патентных документах за 1994 --2007 гг., реализованы на основе двоичных логических и запоминающих элементов в совокупности с дискретными компонентами. Подобные решения исключают их реализацию в микроэлектронном исполнении, а функциональное и структурное решения предлагаемых троичных триггеров не допускает построение на их основе троичных триггеров с различными таблицами переходов и организацией.

Таким образом, вопрос построения троичных запоминающих элементов, которые позволяли бы строить устройства, чьи характеристики (сложность, быстродействие, надежность, экономичность и т.д.) были бы, по крайней мере, не хуже соответствующих характеристик устройств, использующих двухуровневый принцип кодирования, по-прежнему далек от своего решения. А учитывая, что число троичных триггеров с двумя логическими входами (число триггеров с различной таблицей переходов) равно 3 ²⁷ , то вопрос построения троичных триггеров в его сколь-нибудь исчерпывающей полноте требует отдельного самостоятельного исследования.

В двоичной логике нашли применение триггерные схемы с различной структурной организацией: асинхронные триггеры (запоминающие ячейки), синхронные триггеры со статическим управлением записью, синхронные двухступенчатые триггеры, синхронные триггеры с динамическим управлением записью. В каждой организации триггеры подразделяются по реализуемым таблицам переходов: RS-, D-, DV-, JK-, T-триггеры, то есть число используемых триггеров в практике проектирования цифровых устройств достаточно велико.

Ниже предлагается построение трёхстабильных элементов хранения на основе логических троичных элементов, как это имеет место в двоичной логике. Полученные результаты необходимы для разработки и реализации троичных цифровых устройств с памятью, а также для разработки троичных систем моделирования.

Троичная запоминающая ячейка — трит-тер. В двоичной логике всё многообразие структур триггерных схем использует простейший элемент хранения — запоминающую ячейку (ЗЯ).

Запоминающая ячейка — это схема, имеющая два выхода Q и Q , разрешённые сигналы на которых всегда противоположны, и два входа S (Set — установка) R (Reset — сброс). Переключающий сигнал по входу S устанавливает ЗЯ в состояние 1( Q =1, Q =0),аповходу R — в состояние 0( Q =0, Q =1). Обычно она состоит из двух логических элементов, которые взаимно охвачены обратной связью (рис. 1).

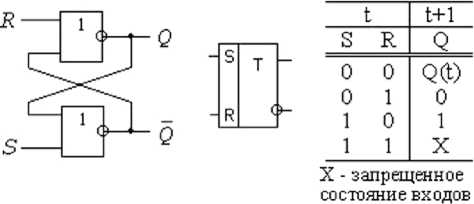
Рис. 1. Запоминающая ячейка на элементах ИЛИ-НЕ, условное графическое обозначение и таблица переходов

Запоминающую ячейку называют асинхронным RS-триггером. Такое название объясняется способом записи информации. Состояние асинхронного триггера определяется в каждый момент времени состоянием входов, то есть изменения входного сигнала непосредственно передаются на выход триггера.

Естественно предположить, что и в троичной логике должна существовать аналогичная запоминающая ячейка (трёхстабильный элемент хранения).

Назовём трёхстабильную запоминающую ячейку триттером . Данный неологизм вводится для краткости и удобства обозначения трёхстабильных элементов хранения. Таким образом, трит-тер — это элемент хранения трита, обозначающего в литературе единицу информации в троичной логике ( ± 1 и 0 или 0 , 1 и2).

Поскольку в троичной логике имеет место три значения, то и триттер должен иметь три выхода 1 Q , 2 Q , 2 Q с тремя различными состояниями (по аналогии с выходами Q и Q у двоичного триггера).

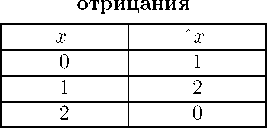
Определим значения, которые должны иметь эти три выхода, используя функцию циклического отрицания (табл. 1).

Т аблица 1

Функция циклического

В табл. 2 приведены возможные (разрешённые) значения трёх выходов триттера. Любые другие сочетания значений выходов триттера будем считать ошибочными (запрещёнными).

Т аблица 2

Значения

выходов триттера

Выходы триттера
1 Q	2 Q	2 Q
0	1	2
1	2	0
2	0	1

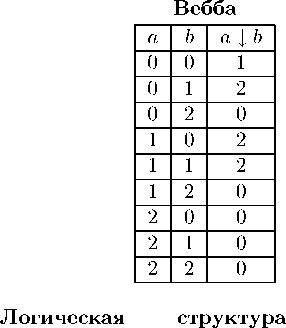
Выбор элементной базы. Для построения триттера выберем, как и в случае двоичной логики, одноэлементный базис, а именно, троичный элемент, реализующий функцию Вебба (табл. 3).

Таблица 3

Функция

триттера.

Предлагается следующая структура триттера (рис. 2), построенная на троичных элементах, реализующих функцию Вебба. В условном графическом обозначении данных троичных элементов добавлена буква Т (троичный), которая отличает троичный элемент от двоичного. Триттер имеет три входа R , S , M и три выхода 1 Q , 2 Q , 2 Q , состояния которых определяются функцией циклического отрицания. По входу R (reset) трит-тер устанавливается в состояние 012; по входу S (set) триттер устанавливается в состояние 120; по входу M (minus) триттер устанавливается в состояние 201.

Полное исследование данной структуры путём моделирования позволило составить таблицу переходов триттера (табл. 4).

Таблица 4

Таблица переходов триттера

Время t           Время t +1 Прим.

R 0	M 0	S 0	1 Q 0	2 Q 1	2 Q 2	1 Q 0	2 Q 1	2 Q 2	Хран
1	0	0	0	1	2	0	1	2	Хран
2	0	0	0	1	2	0	1	2	Хран
0	0	1	0	1	2	0	1	2	Хран
1	0	1	0	1	2	0	1	2	Хран
2	0	1	0	1	2	0	1	2	Хран
0	0	2	0	1	2	1	2	0	Уств1
0	1	0	0	1	2	1	2	0	Уств1
0	2	0	0	1	2	2	0	1	Уств2
0	0	0	1	2	0	1	2	0	Хран
0	1	0	1	2	0	1	2	0	Хран
0	0	1	1	2	0	1	2	0	Хран
0	1	1	1	2	0	1	2	0	Хран
0	0	2	1	2	0	1	2	0	Хран
0	1	2	1	2	0	1	2	0	Хран
2	0	0	1	2	0	0	1	2	Уств0
0	2	0	1	2	0	2	0	1	Уств2
1	0	0	1	2	0	2	0	1	Уств2
0	0	0	2	0	1	2	0	1	Хран
0	1	0	2	0	1	2	0	1	Хран
0	2	0	2	0	1	2	0	1	Хран
1	0	0	2	0	1	2	0	1	Хран
1	1	0	2	0	1	2	0	1	Хран
1	2	0	2	0	1	2	0	1	Хран
0	0	1	2	0	1	0	1	2	Уств0
2	0	0	2	0	1	0	1	2	Уств0
0	0	2	2	0	1	1	2	0	Уств1

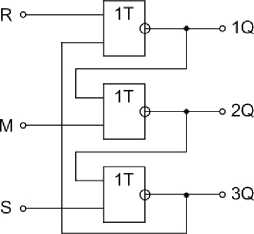
Рис. 2. Логическая схема триттера и его условное графическое обозначение

В этой таблице отражены только разрешённые переходы. Переходы, которые приводят к нарушению ранее определённых разрешённых значений выходов триттера (табл. 2), в таблице переходов триттера не показаны.

Внимательное рассмотрение полученной таблицы переходов триттера позволяет сделать ряд важных выводов относительно свойств предлагаемой структуры триттера.

• 1.    Триттер может находиться в одном из трёх устойчивых состояний:

• 2.    Из 27 возможных входных состояний для каждого из трёх разрешённых состояний выходов

• 3.    Хранение любого из трёх состояний тритте-ра возможно при 6 различных состояниях его входов (табл. 4 строки таблицы переходов с примечанием «Хран»). Это обстоятельство потенциально может быть использовано для упрощения проектируемых структур с использованием данного триттера.

• 4.    Среди трёх групп 6 различных состояний входов триттера, обеспечивающих хранение текущего состояния, только одно входное состояние входит в каждую группу, гарантируя хранение любого состояния триттера. Это входное состояние RMS = 000 (табл. 4). Очевидно, это состояние входов должно быть исходным.

• 5.    Переход из любого текущего состояния в одно из двух других состояний реализуется изменением 0 → 2 одного из входов:

1 Q 2 Q 2 Q = 012 , 120 или 201. Распределение значений по выходам триттера подчиняется функции циклического отрицания. Следовательно, достаточно знать только состояние одного выхода, чтобы определить состояние остальных выходов триттера.

триттера только 9 состояний (табл. 4) не приводят к нарушению ранее определённых разрешённых значений выходов триттера.

• —    по входу R триттер переходит в состояние 012,

• —    по входу S — в состояние 120,

• —    по входу M — в состояние 201.

Часть переходов дублируется изменением 0 → 1 одного из входов (табл. 4), что также может быть использовано для упрощения проектируемых структур с использованием данного трит-тера. Таким образом, триттер реализует полноту переходов.

Моделирование логической структуры триттера. Проиллюстрируем вышеназванные свойства предлагаемой структуры триттера моделированием троичных функций с помощью кодирования в двоичном виде на программируемой логической интегральной схеме (ПЛИС) с использованием САПР фирмы Xilinx и отработкой на стенде с использованием ПЛИС S 10PC84. В этом представлении существует несколько вариантов кодировки, но в любом случае на два бита приходится один трит и ещё один уровень остаётся неопределённым.

Общий подход к синтезу схем реализации троичных функций с помощью кодирования в двоичном виде рассмотрен в работах [7] и состоит в следующем. Составляется таблица истинности для трёхзначной функции в соответствии с выбранной кодировкой. На основе этой таблицы для каждого выходного разряда составляется карта Карно для минимизации функции. По результатам минимизации производится синтез схемы.

Примем следующее двоичное кодирование трёхзначного алфавита: 0 — 00, 1 — 01, 2 — 10. Логическая схема, реализующая функцию Вебба, приведена на рис. 3. Здесь же приведено условное графическое обозначение троичного элемента NOR (элемент ИЛИ-НЕ) в библиотеке макроэлементов. Временная диаграмма работы троичного элемента NOR приведена на рис. 4.

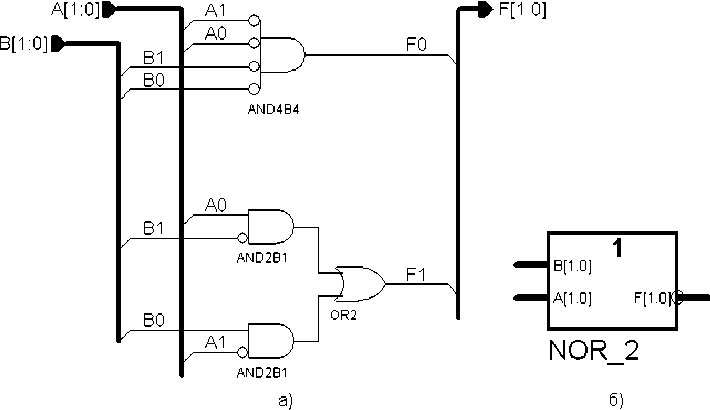
Рис. 3. Троичный элемент NOR, реализующий функцию Вебба: а) логическая схема; б) условное графическое обозначение

ЩШШ| Ins/div |LLUJ|

0.0

	10ns	20ns	30ns	40ns	50ns	60ns	70ns	80ns
111 111111	11H111 и	111111111	> 1 l 1 1 И l 1	i 11111111	1 1 И 1 1 1 1 1	111111111	111111111	111111111

Fl...#2

DI...Cs 2

Bl...#2 Cs 2

_0____	Xi	X2	Xo	Xi	X2	Xo	Xi	X2
0 ___			Xi			X2
1		Xo			Xo

Рис. 4. Временная диаграмма троичного элемента NOR

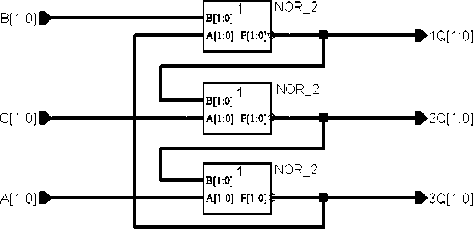
Рис. 5. Логическая схема триттера

TRIT

— A[1:0) 1Q[10] —

— B[1;0] 2Q(1:0] —

— C[1:0] 3Q[1:0] —

TRIT

Рис. 6. Условное графическое обозначение триттера

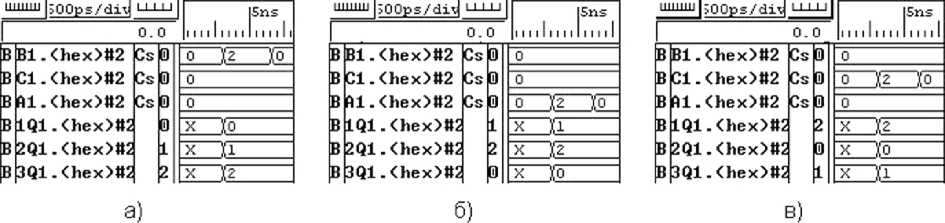
Рис. 7. Временные диаграммы установки триттера в требуемое состояние: а) в состояние 012 по входу B ; б) в состояние 120 по входу A ; в) в состояние 201 по входу C

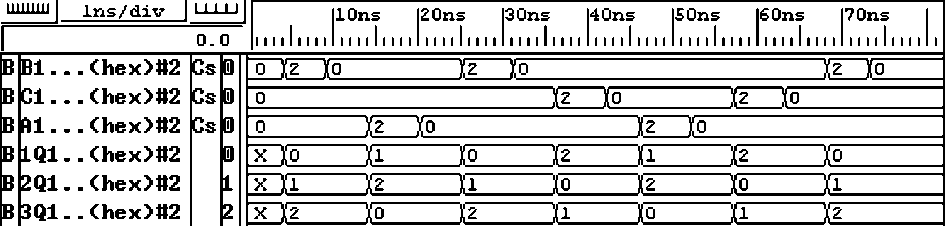
Рис. 8. Временная диаграмма переходов триттера при изменении входных сигналов из 0 в 2

lllllllll I

SOOps/div | ljuuu

lllllllll

Sns iiiiIiiii

10ns iiiiIiiii

ISns iiiiIiiii

20ns iiiiIiiii

25ns iiiiIiiii

30ns iiiiIiiii

35ns iiiiIiiii

40ns Hill

0.

0

Bl..

.#2 Cs

0

0   12

Xo

X1

So

3

Cl..

.#2 Cs

0

0

Xi

Xo

в

Di..

.#2 Cs

0

0

X1

Xo

1Q1.

.#2

0

x Xo

Xi

X2

Xo

2Q1.

.#2

1

x Xi

Xz

Xo

Xi

3Q1.

.#2

2

x к

Xo

Xi

X2

Рис. 9. Временная диаграмма переходов триттера при изменении входных сигналов из 0 в 1

К	2
	Л
	ф
UI	E
Ci
E	>x
Q	о
z Ф X О	m
	ф E

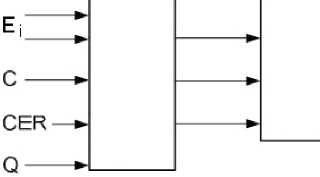
Рис. 10. Обобщенная схема реализации двухступенчатого троичного триггера с разрешением и асинхронной установкой в 0

TRIT
A[1:0]	1Q[T0]
B[T0]	2Q[1:0]
C[1:0]	3Q[1:0l

Q1

С---►

CER—►

TRIT
B[1:0]	2Q[1:0]	--►
C[1:0]	3Q[1:0]	--►

1Q[1:0]

2Q[1:0]

3Q[1:0]

CER—H

Q

1Q[1:0]

2Q[1:0]

3Q[1:0]

CER—►

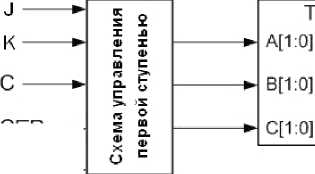
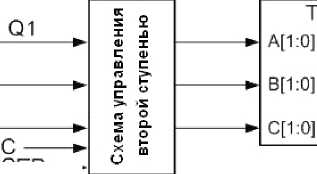
Рис. 11. Обобщенная структура синхронного двухступенчатого троичного JK-триггера с разрешением и асинхронной установкой в 0

* Q

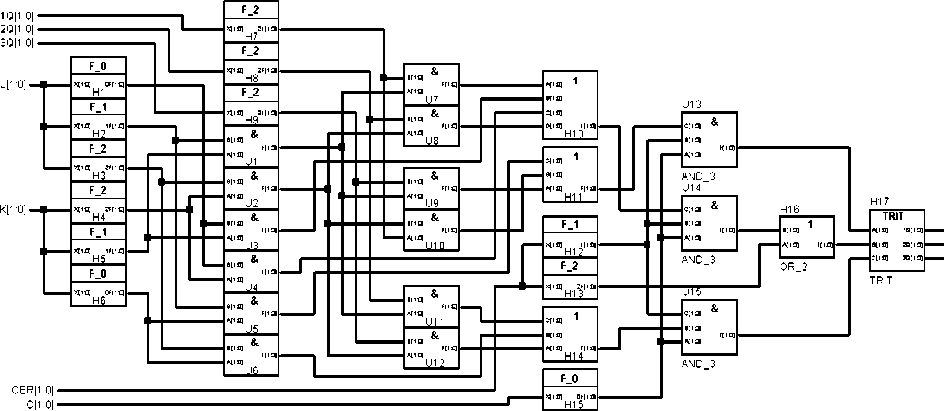
Рис. 12. Логическая схема реализации первой ступени двухступенчатого троичного JK-триггера

На рис. 5 представлена логическая схема трит-тера, реализованная на макроэлементах NOR_2. На рис. 6 приведено условное графическое обозначение триттера.

Диаграммы на рис. 7 иллюстрируют переход триттера из первоначального неопределённого состояния в требуемое по установочным входам B , A , C .

Видимо, целесообразно внешним входам трит-тера дать мнемоничные имена, как это имеет ме- сто для двоичной запоминающей ячейки. Например, В заменить на R (reset) — по данному входу триттер устанавливается в состояние 012; А заменить на S (set) — по этому входу триттер устанавливается в состояние 120; C заменить на M (minus) — по этому входу триттер устанавливается в состояние 201.

Временная диаграмма, приведённая на рис. 8, демонстрирует переходы триттера из каждого состояния в два других состояния при изменении входных сигналов из 0 в 2, диаграмма рис. 9 — при изменении входных сигналов из 0 в 1.

На основе созданной троичной запоминающей ячейки (триттера) можно спроектировать троичный триггер с произвольной таблицей переходов и требуемой структурной организацией.

Синтез синхронных двухступенчатых троичных триггеров. Триггер — один из базовых (основных) элементов цифровой техники. Некоторые исследователи включают триггер в 100 великих изобретений.

Триггер не является логическим элементом первого уровня, а сам состоит из логических элементов первого уровня — инверторов или логических вентилей. По отношению к логическим элементам первого уровня триггер является логическим устройством второго уровня.

В практике проектирования цифровых устройств широко используются синхронные триггеры с различной таблицей переходов. Эти триггеры, как правило, имеют различные дополнительные управляющие входы: вход разрешения по C -входу, синхронные или асинхронные входы предварительной установки триггера в то или иное состояние.

Использование трёхзначной логики позволяет сократить число дополнительных управляющих входов без сокращения необходимых управляющих функций (микроопераций), выполняемых по этим входам.

Рассмотрим алгоритм синтеза синхронных двухступенчатых троичных триггеров с заданной таблицей переключений на примере троичного триггера, работающего в соответствии с его двоичным аналогом JK-триггером.

Обобщенная схема реализации двухступенчатого троичного триггера приведена на рис. 10.

В основе реализации лежат две троичных запоминающих ячейки. Вместе со своей схемой управления они образуют соответственно первую и вторую ступень синхронного двухступенчатого троичного триггера.

Двухступенчатый троичный триггер имеет три группы входов:

• —    E i — сигналы переключения троичного триггера, задающие логику переключений состояния троичного триггера;

• —    CER — управляющие сигналы — в данном случае во входе CER объединены две микрооперации: разрешение ( CE ) при CER = 1 и асинхронный сброс ( CLR ) при CER = 2;

• —    C — синхронизирующий сигнал.

Схемы управления преобразуют соответственно информацию, поступающую на входы E i троичного триггера, и текущее состояние первой ступени в сигналы, которые подаются на установочные входы соответствующей троичной запоминающей ячейки.

Вход C — вход для синхронизирующего сигнала. Импульсы, поступающие на этот вход, опре- деляют момент приёма троичным триггером соответствующей информации. Сигналы, поступающие на вход C , логической информации не несут, а являются сигналами синхронизации. Ступени двухступенчатого троичного триггера работают в «противофазе», то есть если первая ступень изменяет свою информацию, то вторая ступень хранит своё состояние, и, наоборот, — если вторая изменяет своё состояние, то первая хранит своё.

Состояние первой ступени в рассматриваемой структуре троичного триггера изменяется только тогда, когда значение синхросигнала соответствует нулю. Состояние второй ступени изменяется при значении синхросигнала равном единице. Это означает, что при C = 0 переключения сигналов на логических входах E i вызывает изменение состояния первой ступени. Поэтому информацию на логических входах, как правило, меняют в данном случае при C = 1.

Вход CER (clock enable, reset) — вход разрешения работы троичного триггера и асинхронной установки ступеней троичного триггера в 0.

Далее для примера рассмотрим реализацию синхронного двухступенчатого троичного JK-триггера с асинхронной установкой в ноль.

Синтез синхронного двухступенчатого троичного JK-триггера. Структуру синхронного двухступенчатого троичного JK-триггера с асинхронной установкой в 0 можно представить в виде двух троичных запоминающих ячеек (трит-теров) и двух схем управления (рис. 11).

В двоичной логике JK-триггер является универсальным триггером. У него наиболее полный набор функций: хранение, установка в 0, установка в 1, инверсия текущего состояния. Аналогично, в троичной логике JK-триггер имеет следующий набор функций: хранение при J = K = 0; установка в 0 при J = 0, K = 1 или 2; установка в 1 при J = 1, K = 0; установка в 2 при J = 2, K = 0; циклический сдвиг текущего состояния при J = 1, K = 1; двойной циклический сдвиг текущего состояния при J = 2, K = 2.

Ниже приведена таблица переходов синхронного двухступенчатого троичного JK-триггера с асинхронной установкой в 0 (табл. 5).

В данной таблице Q — состояние второй ступени, то есть выхода JK-триггера, а Q 1 — состояние первой ступени. Символом « » обозначается циклический сдвиг. C оответственно « » означает двойной циклический сдвиг.

В соответствии с описанной логикой работы JK-триггера и законом функционирования троичной запоминающей ячейки (триттера) таблицу истинности схем управления первой и второй ступеней можно представить в следующем виде (табл. 6 и7).

Cхемы управления наиболее просто реализовать в базисе Россера–Тьюкетта. Их реализации приведены на рис. 12 и 13.

U16

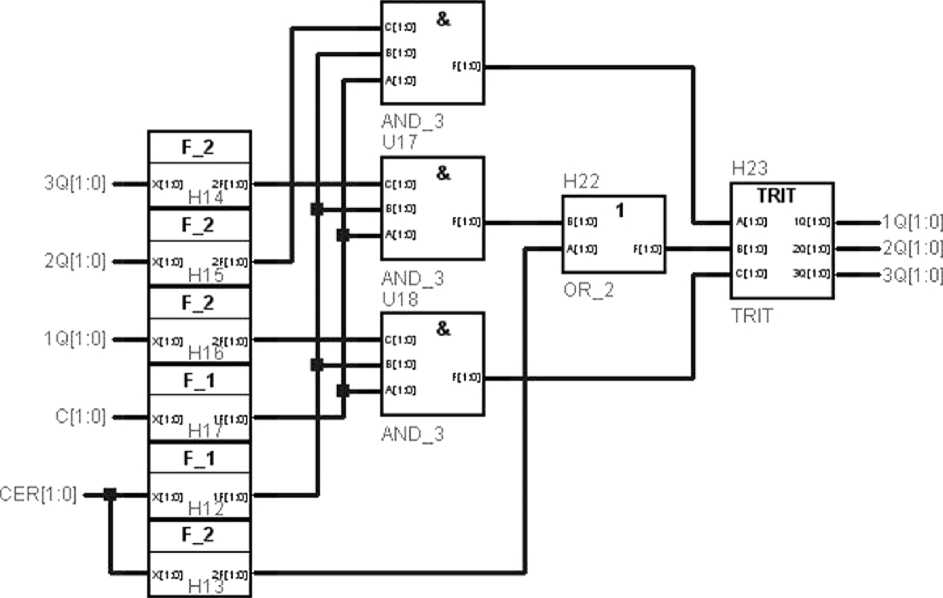
Рис. 13. Логическая схема реализации второй ступени двухступенчатого троичного JK-триггера

Таблица 5

Таблица переходов двухступенчатого JK-триггера с асинхронной установкой в 0

CER	C	J	K	Q i+i	Q t +1	Пояснение
0	Х	X	Х	Q i	Q t	Запрет работы по C -входу (хранение)
2	Х	X	Х	0	0	Асинхронная установка в 0
1	0	0	0	Q t	Q t	Загрузка состояния второй ступени в первую
1	0	0	1	0	Q t	Синхронная установка первой ступени в 0
1	0	0	2
1	0	1	0	1	Q t	Синхронная установка первой ступени в 1
1	0	2	0	2	Q t	Синхронная установка первой ступени в 2
1	0	1	1	Q t	Q t	Загрузка сдвинутого состояния второй ступени в первую
1	0	2	2	Q t	Q t	Загрузка дважды сдвинутого состояния второй ступени в первую
1	0	2	1	Х	Х	Запрещенные состояния
1	0	1	2	Х	Х
1	1	Х	X	Q i	Q i	Загрузка состояния первой ступени во вторую ступень

Таблица 6

Таблица истинности схемы управления первой ступени

Входы				Выходы			Выход первой ступени
CER	C	J	K	A	B	C	Q 1 +1
0	X	X	Х	0	0	0	Q i
2	X	X	X	0	2	0	0
1	0	0	0	2, при Q t = 1	2, при Q t = 0	2, при Q t = 2	Q t
1	0	0	1	0	2	0	0
1	0	0	2
1	0	1	0	2	0	0	1
1	0	2	0	0	0	2	2
1	0	1	1	2, при Q t = 0	2, при Q t = 2	2, при Q t = 1	Q t
1	0	2	2	2, при Q t = 2	2, при Q t = 1	02, при Q t = 0	Q t
1	1	X	X	0	0	0	Q i

Таблица 7

Входы				Выходы			Выход второй ступени
CER	C	J	K	A	B	C	Q t +1
0	X	X	Х	0	0	0	Q t
2	X	X	X	0	2	0	0
1	0	X	X	0	0	0	Q t
1	1	X	X	2, при Q 1 = 1	2, при Q 1 = 0	2, при Q 1 =2	Q 1

Таблица истинности схемы управления второй ступени

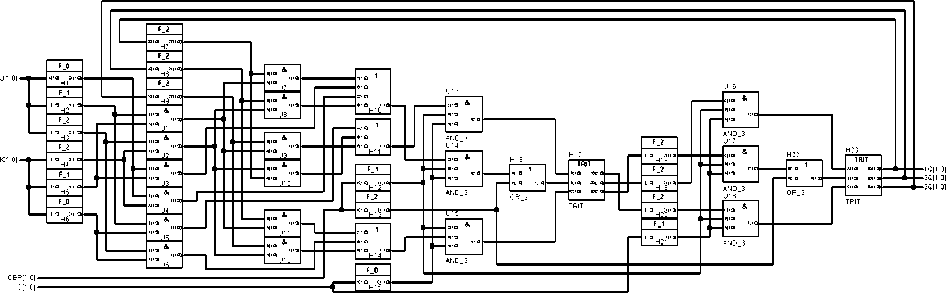
Рис. 14. Логическая схема синхронного двухступенчатого троичного JK-триггера

ШШШ| 2ns/div LJJJJ|

0. о

ВG1- -.#2 0= f

ВCERl.#2 Cs L

в

J0...#2 Os 2

В KI.,.#2 0=2

В

LQ1..#2

В2Ql..#2

В3Q1..B2

В В в в в в в в в в в в в

B^23-3Ql.

□

2 □

2 □ □

2 □ О

2 □ □ □ □

Рис. 15. Временная диаграмма работы синхронного двухступенчатого троичного JK-триггера с асинхронной установкой в 0

Элемент H17 в логической схеме первой ступени является запоминающей ячейкой. Все остальные элементы — схема управления первой ступенью. Элемент H16 позволяет подать сигнал асинхронной установки в 0 при CER = 2. Элементы U13, U14, U15 реализуют синхронизацию управляющих сигналов (передача сигналов установки первой ступени при C = 0, передача сигналов хранения при C = 0) и разрешение работы при CER = 1.

Элементы H10, H11 и H14 формируют установочные сигналы первой ступени. Элемент U7 формирует установочный сигнал первой ступени в 0 при текущем состоянии второй ступени, равном 2, и циклическом сдвиге. U8 — также установочный сигнал первой ступени в 0 при текущем состоя- нии второй ступени, равном 1, и двойном циклическом сдвиге. Аналогично, U9 — сигнал установки в 1 при текущем значении 0 и циклическом сдвиге, U10 — сигнал установки в 1 при текущем значении 2 и двойном циклическом сдвиге; U11 — сигнал установки в 2 при текущем значении 1 и циклическом сдвиге, U12 — сигнал установки в 2 при текущем значении 0 и двойном циклическом сдвиге. U3 и U4 — синхронная установка в 0, U5 — синхронная установка в 1, U6 — синхронная установка в 2.

При подаче на управляющие входы запрещённых состояний троичный JK-триггер при данной организации будет хранить текущее значение первой ступени, так как на входы элемента H23 будут поступать нулевые сигналы.

Элемент H23 — запоминающая ячейка второй ступени. Элемент H22 второй ступени, аналогично элементу H17 первой ступени, позволяет подать сигнал асинхронной установки в 0 при CER = 2. Элементы U16, U17 и U18 реализуют синхронизацию управляющих сигналов (передача сигналов установки второй ступени при C = 1, передача сигналов хранения при C = 1) и разрешение работы при CER = 1.

На рис. 14 приведена логическая схема синхронного двухступенчатого троичного JK-триггера с асинхронной установкой в 0. Временная диаграмма работы троичного JK-триггера показана на рис. 15.

Аналогично представленной реализации двухступенчатого троичного JK-триггера можно синтезировать и реализовать двухступенчатый троичный триггер с любой таблицей переходов.