Tuning Schema Matching Systems using Parallel Genetic Algorithms on GPU

Published Online November 2010 in MECS

Schema matching is the task of finding semantic correspondences, i.e. matches, between disparate metadata structures. It is a key problem in numerous applications, such as e-commerce, data warehousing, web-oriented data integration, schema evolution and migration, and peer-to-peer data management [1].

Traditionally, schema matching is performed manually, and it is a labor-intensive, time-consuming, and error-prone process. Thus researchers have developed various matching techniques and prototypes, i.e. matchers, which exploit element names, data types, descriptions, schema structures, and other types of information to find matches between schemas (see Ref. [1]—[3] for recent surveys). None of these matchers outperforms all the others on all existing benchmarks (like XBenchMatch [4]). Therefore, many matching systems (e.g., Ref. [5]—[9]) combine

Corresponding author: Lei Zhao.

multiple matchers, called matching components, to achieve better matching results. The multi-component nature makes matching systems extensible and customizable, however, as pointed out in Ref. [10], it also brings a tuning problem that is to determine which components to execute and how to adjust the knobs (e.g., thresholds, weights, etc.) of these components, for given matching situation.

In this paper, we consider the tuning problem as an optimization problem. We describe an approach to automatically tune schema matching systems using genetic algorithms. Given a schema S and a matching system M, we first generate a synthetic workload W which consists of a set of matching scenarios involving S , then apply M to scenarios in W and learn the best configuration using genetic algorithms. We implement parallel genetic algorithms on consumer-level GPU based on NVIDIA’s Compute Unified Device Architecture (CUDA) and promote the performance of genetic algorithms.

The main interesting features of our approach are:

• •    Learning a configuration which effectively improves the performance of a matching system with genetic algorithms. We allow users to make a trade-off between precision and recall while evaluating the performance of a configuration candidate.

• •    Providing a matching scenario generator which produces various matching scenarios for the input schema. It handles both relational and XML schemas, and it can be used as a training set generator for other learning-based matchers.

• •    Implement parallel genetic algorithms using consumer-level GPU based on CUDA, and optimize the performance of genetic algorithms with low exact cost.

• •    Experiments over four real-world domains with two main matching systems demonstrate that our approach provides more qualified matches over different domains.

The rest of the paper is organized as follows. Section 2 briefly surveys related work. Section 3 focuses on the drawbacks of existing solutions and the motivation of our work. Section 4 contains an overview of our approach. Section 5 describes the implementation on GPU. The results of experiments that show the performance of our approach are presented in section 6. Finally, section 7 gives a conclusion.

• II.    RELATED WORK

  Schema matching has received increasing attention since 1990s. Various matching techniques and prototypes have been developed. These techniques exploit information such as element names, data types, structures, number of sub-elements, integrity constraints, and instance data to find semantic correspondences between schemas (see Ref. [1]—[3] for recent surveys). Beyond the schema and instance data information, several types of external evidence have been exploited, like past matches [5, 6] and usage information [11] — [13].

Obviously, an effective matching solution should employ many of the techniques, each on the type of information that it can exploit. Some recent works (e.g., Ref. [5], [7]—[9]) have described a system architecture that employs multiple matchers, each of which exploits well a certain type of information mentioned above. Such multi-component matching systems are extensible and customizable for a particular application domain [14, 15]. However, there is another serious problem for domain users: given a particular matching task, how to choose the most suitable components to execute, and how to set the multiple knobs (e.g., thresholds, weights, coefficients, etc.) . This problem is called the schema matching systems tuning problem .

Lately, several researchers present their solutions to solve the tuning problem of multi-component matching systems. In Ref. [16], F. Duchateau et al. present a factory which generates matchers according to user requirements. The factory learns how to apply the similarity measures and classifiers to achieve high matching quality based on matched schemas and expert matches provided by users. The factory could build a specified matcher for a given matching situation. In Ref. [17], A. Marie et al. propose an approach to combining matchers into to ensembles. They use the boosting algorithm which is a machine learning technique to select matchers that participate in an ensemble. The combined matchers could achieve better result than random schema matchers. F. Duchateau et al. describe a method which chooses a set of matchers to execute using decision tree algorithm [18]. The training process is also based on expert correspondences provided by domain users. Y. Lee et al. present the eTuner framework which mainly concerns relational schema matching problems [10]. eTuner generates a synthetic workload by perturbing input schemas randomly, and then finds the best configuration using staged greedy search method. In Ref. [19], E. Peukert et al. optimize the schema matching process using rewrite technique, which is often used in database query optimization. They represent the matching process as a directed graph model, and choose the components with lower cost using filter-based rewrite rules.

Some of the existing solutions focus on quickly developing robust matchers for a particular matching situation (e.g., Ref. [16, 17]). And others attempt to customize existing matchers for a given matching situation (e.g., Ref. [10], [18, 19]). Our work can be seen as a part of customization techniques. We are aiming at automating the customization using learning techniques, and reducing the high total cost of schema matching process.

• III.    MOTIVATION

As previously mentioned, increasing matching systems employ multiple matchers to produce better matching results. However, without tuning, a matching system tends to produce inferior performance, because it cannot exploit domain characteristics. While necessary essential, tuning is difficult for domain users, due to the wide variety of matching techniques employed and the large number of knobs involved.

Although some researchers have proposed their solutions to the tuning problem, there are still two major drawbacks. First, some solutions require domain users to provide a knowledge base consists of matched schemas and expert correspondences (e.g., Ref. [16-18]). This requirement makes the solutions involve much manual effort. E-Tuner could generate synthetic workload automatically, but it only considers matching systems that handle relational representations. In fact, most multicomponent matching systems could also handle other types of data representations, such as XML schemas, ontology, web forms, etc. Second, the configuration found by existing solutions sometimes is actually local optima rather than the global optimum of the tuning problem. To find out the best configuration, a better search strategy should be applied.

To solve previously mentioned drawbacks, our approach aims at designing a workload generator for both relational and XML schemas and searching the configuration space with genetic algorithms.

As pointed in Ref. [10], the challenge of workload generator is to develop perturbing rules for particular data representation. We represent input schemas with general data model and define a set of perturbing rules for both relational and XML schemas. On the other hand, genetic algorithms (GAs) have been demonstrated efficient search methods for solving wide-range of real-world problems, since introduced in 1960s. Although cannot be proofed in mathematics, GAs are still considered as powerful tools for optimization problems [20]. A recent study has shown that GAs has certain stability and it could improve the reliability by reiteratively computation and estimate the effects of improvements [21]. GAs might take a long time to find good solutions for some difficult problems. A promising approach to overcome this problem is to parallelize GAs [22]. Recently, several researchers have implemented parallel genetic algorithms (or parallel evolutionary algorithms) on graphics processing units (GPUs), and have demonstrated GPUs have a potential for acceleration of GAs (see Ref. [23] — [26] for more details).

• IV.    OVERVIEW

Fig. 1 shows the architecture of our approach. There are two main modules: a workload generator which produces a synthetic workload W for the input schema S and a GA-based tuner which searches for the most suitable configuration of matching system M.

The rest of this section describes the workload generator and GA-based tuner in detail.

• A.    Workload Generator

Given a schema S and the workload size n , the generator returns a set of matching scenarios as the synthetic workload W. The data model used internal by the generator is the nested relational model which is sufficiently general for both relational and XML schemas.

Definition 1: A matching scenario is a triple ( S , T , Q ) , where S is a source schema, T is a target schema, and Ω is a set of semantic correspondences between S and T .

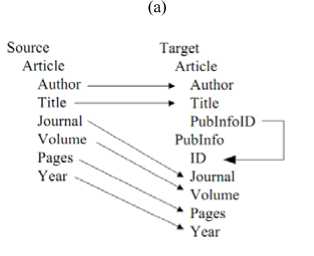
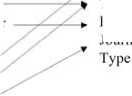
• 1)    Create schema pairs ( S , T ) , ( S , T₂ ) , k , ( S , T n ) : the workload generator creates matching scenarios by composing basic scenarios in different ways and perturbing element names and data types of S randomly. We define four basic matching scenarios: Copying , Merging , Vertical Partition , and Nesting according to the basic mapping scenarios described in Ref. [27] and real-world schema matching specifications. The generator has implemented a set of common name transformation rules. Examples include replacing a name with a common abbreviation or a synonym obtained from WordNet database¹, and dropping prefixes or suffixes. The generator has also specified transformation rules between different data types. Fig. 2 presents examples of basic matching scenarios and perturbations.

The workload generator allows a user to tune the generated matching scenarios through a set of composition parameters. The composition parameters consist of 4 repetition parameters Я (one for each basic the depth of generated schemas), along with 2 standard deviation parameters D. Every parameter in C is in fact the mean value of a Gaussian distribution whose standard deviation is the value of the corresponding parameter in D.

• 2)    Create semantic correspondences Q Q 2 , к , Q n : The workload generator retraces the generation history to create Ω, which is a set of correct semantic correspondences between S and T_i . Briefly, if element t of T i is created from elements s ₁, s ₂, K s_k of S , then we create { s 1 = t , s ₂ = t , k , s k = t } as Q i .

The generator could exploit auxiliary information 7, such as global schemas, expert matches, and dictionaries, to build a better workload, which improves the GA-based tuning performance. Fig. 3 gives a pseudo code description of the workload generator.

• B.    GA-based Tuner

As previously described, our objective is to find out a configuration of matching system M, which optimizes the performance over a synthetic workload W, from a potentially huge space. To address this problem, we propose a tuning approach using the genetic algorithms. Genetic algorithms are a family of computational models inspired by evolution. These algorithms encode a potential solution to a specific problem on a simple chromosome-like data structure and apply recombination operators (e.g. crossover operator and mutation operator) to these structures so as to preserve critical information. Genetic algorithms are often viewed as function optimizers and could always locate good solutions in reasonable amounts of time [20]. Fig. 4 shows the prototype of GA-based tuner.

• 1)    Initialize the population: Most GA practitioners use bit-string representations to represent potential solutions. We could represent a potential configuration as a chromosome with multiple genes, each of which reflects a knob of the configuration. When initializing, the population is generated randomly.

  Composition Parameters

  
  

  SchemaS---►

  
  

  Workload Generator

  
  

  Synthetic

  Workload

  
  

  Tuning Parameters

  

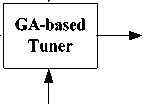
  Tuned Matching System M

  Matching System M

  
  

  A uxiliary Information

  
  

  Figure 1. Architectural overview: This figure shows the main modules of our approach.

  scenario mentioned above), 2 construction parameters C (specify the number of sub-elements of an element and

  
  

  1: Cognitive Science Laboratory, Princeton University. WordNet: A Lexical Database for the English Language,

  
  

  Source                   Target

  Article                  * Article

  ArticlelD: int          ►  ID: number

  Title: string   —— ^r  NameOfAuthor: varchar

  Author: string"*  Title: varchar

  Year: int -----------*  YOP: date

  
  
  
  
  

Source

Book Author Title Publisher

Article Author Title Journal

Target Article Book

—> Author Title Publisher Journal

(b)

Source             Target

Article               Article

• ■ AuthorlD _x /^ Title

Title          „ v Journal

Journal "'           Author

Author              * ID

• ► ID           . * Name

Name -

• (c)                                                  (d)

  Figure 2. Examples of basic matching scenarios. (a) A copying scenario with perturbations on element names and data types. (b) A merging scenario using a column “Type” to identify records from different tables in source schema. (c) A vertical partition scenario which divides a table in source schema into two in the target. (d) A nesting scenario which creates a nested structure from a foreign key definition element in source schema.

  
  
  

• 2)    Evaluate potential solutions: The fitness value of each individual in the population could be determined by the quality of its corresponding matching result. We allow domain users to specify the influence of Precision and Recall in the fitness evaluation.

Definition 2: The fitness function is

_ ,,      , x          Precision x Recall

F - Measure ( a ) = --------------------------- (1)

( 1 - a ) x Precision + ax Recall

α is a preference between Precision and Recall , and 0 <  a <  1. In particular, F - Measure ( a ) ^ Precision , when a ^ 1, and F - Measure ( a ) ^ Recall , when a ^ 0 .

• 3)    Repeat generating process until termination: Our tuner first selects the best-fit individuals and breeds new individuals through crossover and mutation operations, then evaluates the fitness of new individuals, and replaces least-fit population with new individuals. This generating process is repeated until a terminate condition (like time or generations limit, fitness threshold achieved, etc.) has been reached.

• V.    IMPLEMENTATION OF PARALLEL GENETIC ALGORITHMS ON GPU

Parallel genetic algorithms (PGAs) have been considered a promising approach to make GAs faster. However, PGAs are usually applied on parallel, distributed, and networked computers which are not easy to access for many users. Recently, GPUs have become powerful tools for general purpose computing. Since GPUs have already been installed on most ordinary personal computers, the exact cost for using GPUs is quite low. Therefore, we implement PGAs on consumerlevel GPU to promote the performance of tuning process.

The rest of this section presents the architecture of CUDA and our implementation of PGAs on GPU.

• A.    Architecture of CUDA

CUDA (Computer Unified Device Architecture) is a general purpose parallel computing architecture which can be performed on any NVIDIA graphics card from GeForce 8 generation on both Linux and Windows platform. CUDA comes with a software environment that allows developers to use C as a high-level programming language. Therefore, programmers could develop parallelism programs on GPUs with relative ease [28].

CUDA is a platform for massively parallel high-performance computing on NVIDIA’s powerful GPUs. At its cores are three key abstractions – a hierarchy of thread groups, shared memories, and barrier synchronization – that are simply exposed to the programmer as a minimal set of language extensions. These abstractions provide fine-grained data parallelism and thread parallelism, nested within coarse-grained data parallelism and task parallelism. CUDA lets programmer partition the problem into coarse sub-problems that can be solved independently in parallel by blocks of threads, and each sub-problem into finer pieces that can be solved cooperatively in parallel by all threads within the block.

Fig. 5 shows the architecture of CUDA. Thread is basic unit to manipulate data in CUDA. The thread index is a 3-dimesion vector, so that threads can be identified using a one-dimensional, two-dimensional, or threedimensional thread index, forming a one-dimensional, two-dimensional, or three-dimensional thread block. All the threads have access to the concurrently block’s shared memory. Those multi-dimensional blocks are organized into one-dimensional or two-dimensional grids, each block can be identified by one-dimensional or twodimensional index, and all grids share one global memory.

CUDA requires all the active processors to execute the same instruction at the same time but on different data, also called SIMD for Single Instruction Multiple Data. As mentioned above, GAs need to evaluate different individuals in the population using an identical fitness

Grid0

Block0

Block1

Global Memory

Block2

Block3

Grid1

Block0 W^	Block1	Block2 wM
Block3	Block4	Block5
Wi	Wi	4#A

Block4

Block5

Figure 5. The architecture of CUDA.

function and are suitable to be parallelized on the architecture of CUDA.

• B.    Implementation of PGAs on GPU

There are several types of PGAs: global singlepopulation master-slave PGAs, single-population finegrained PGAs, multiple-population coarse-grained PGAs, and hierarchical PGAs [22, 26]. In a master-slave PGA there is a single population, but the evaluation of fitness and/or genetic operators are distributed among several processors. Fine-grained PGAs are suited for massively parallel computers and consist of one population, which has a spatial structure. The interactions between individuals are limited: an individual could only compete and mate with its neighbors. However, the neighborhoods overlap permits some interactions among all individuals. Multiple-population PGAs assume that several subpopulations (demes) evolve in parallel and demes are relatively isolated. These demes exchange individuals occasionally, and the exchange is also called migration. Hierarchical PGAs combine multiple-population PGAs with master-slave PGAs or fine-grained PGAs, and have better performance than any of them alone.

According to the architecture of CUDA, we implement the multiple-population PGAs in a particular way. Initialization: An initial population is generated on CPU and transferred to the global memory of GPU.

• 1)    Partition: The initial population is partitioned into several subpopulations. Each subpopulation is distributed to the shared memory of a thread block.

• 2)    Evolution: Each thread block runs the evolution independently. The implementations of genetic operators, such as selection, crossover, and mutation have been described in Ref. [24]—[26].

• 3)    Migration: The model of migration is singledirection migration. Each thread block transfers its best individuals to its next block. Since every thread block could be identified using thread block index, it is easy to achieve such migration. Fig. 6 shows the migration model of multiple-population PGAs.

• 4)    Update & Termination: The global memory is updated with new individuals. The process would stop if the terminate condition has been reached.

• VI.    EXPERIMENTS

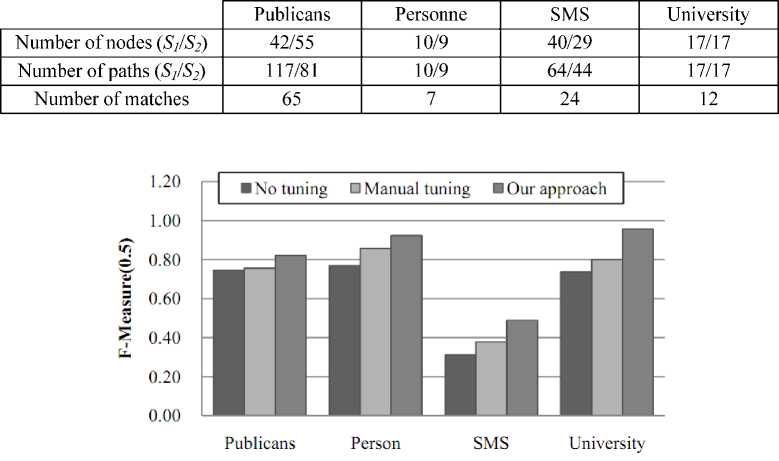
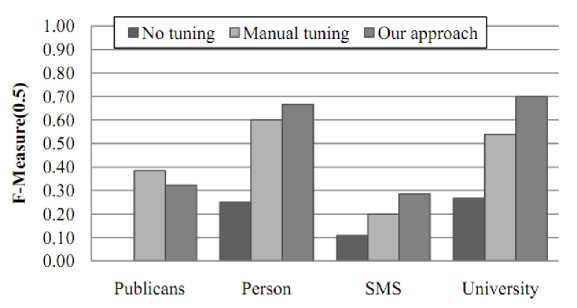
We have evaluated our approach over two common matching systems, COMA++ [5] and SimFlood [29] with similarity metrics from SimMetrics², applied to four real-world XML schema matching tasks. Publicans , Person , and University are available in XBenchMatch benchmark [4]. SMS is provided by YAM as a test case [16]. Detailed features of each task are shown in Fig. 7.

To compare with our approach, we examine other two tuning methods: (1) Applying the off-the-shelf matching systems without any tuning. (2) Manual tuning, by tweaking a few knobs, examining the output of a matching system, and then adjusting the knobs again.

Our experiments are performed using an Intel Core2 Duo T5250 CPU 1024M RAM and an NVIDIA GeForce 8400M GS GPU. To compare with the implementation of

Grid

Block(0,0) —н   Block(0,1) —H  Block(0,2) Block(1,0) H*—I Block(1,1) H*—I Block(1,2)

Figure 6. The migration model in our implementation of multiplepopulation PGAs.

PGAs on GPU, we also implement the tuning process on CPU with the help of JGAP3, a genetic algorithms and genetic programming component provided as a java framework.

To simplify the tuning process, we only consider a few influential knobs of each matching system. This selection is done by applying the attribute selection of Weka4 before running our approach.

We test each method 30 times to limit the impact of randomness. Each time, we generate a synthetic workload with 15--30 scenarios for each matching task. For our approach, we set the preference between precision and recall to 0.5, and the threshold of fitness value to 0.95. We set different values to the population size. Concerning about time consuming, we set the maximized number of generation to 5.

Fig. 7 shows the matching performance of COMA++ and SimFlood. It demonstrates that our method could effectively improve the performance of schema matching systems. However, the performance of a tuned system is relevant to the matching algorithms of the system. For example, the average F-Measure (0.5) value of tuned SimFlood over matching task Publicans is 0.3226 (less than half of the average F-Measure (0.5) value of tuned COMA++, 0.8205), because we do not use any dictionary in this task, and the matching algorithm is mainly driven by the initial textual match.

Fig. 8 shows the effects of population size on the run time when we apply our approach on COMA++ system for the SMS task. We divide the initial population into 2, 4, and 8 subpopulations (thread blocks). Each subpopulation consist 10 individuals (threads). The maximum number of threads per block of our device is 512, and is fair enough for larger subpopulations. The experiment shows that our approach runs faster on GPU especially when larger population involved. However, the run time of tuning process still strongly depends on the matching algorithms and the size of synthetic workload.

TABLE I. SUMMARY OF FOUR XML MATCHING TASKS

(a)

(b)

Figure 7. Matching performance of (a) COMA++ and (b) SimFlood

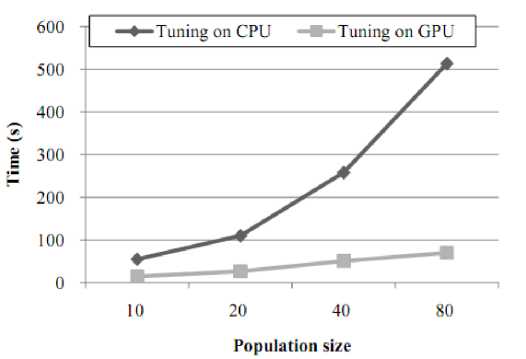
Figure 8. The effects of population size on the run time while tuning COMA++ system for the SMS task.

• VII.    CONCLUSIONS

In this paper, we have presented an approach to automatically tune schema matching systems using genetic algorithms. To promote the performance of our approach, we implement parallel genetic algorithms on GPU based on CUDA. The main contributions of our work are: (1) providing a matching scenario generator for learningbased matchers, and (2) providing better performance by tuning matching systems for particular matching situation. Experiments over four real-world domains with two main matching systems demonstrate that our approach provides more qualified matches over different domains.

ACKNOWLEDGEMENT

The paper is supported by National Natural Science Foundation of China (No. 61073061). The authors are grateful to all the people for helpful suggestions. The authors would like to thank all the anonymous reviewers for their helpful comments on earlier drafts of this paper.